Figure 6.

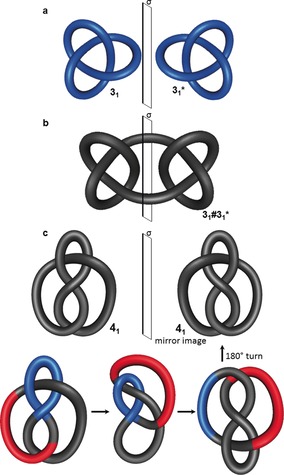
Chirality in knots. a) The trefoil knot 3₁ is topologically chiral, as it cannot be deformed to its mirror image form 3₁* without the strand passing through itself. b) The square knot 3₁#3₁*, a composite knot obtained by connecting two trefoil knots of opposite handedness, is achiral, as the mirror plane σ projects it onto itself. c) The figure‐eight knot 4₁ can be transformed into its mirror image. By flipping the part shown in red over the part shown in blue, an upside‐down version of the mirror image is obtained after deformation, thereby making it topologically achiral. For the sake of brevity, not every Reidemeister move is shown here for this transformation.