Figure 2. High-contrast bursts drive maximal encoding.
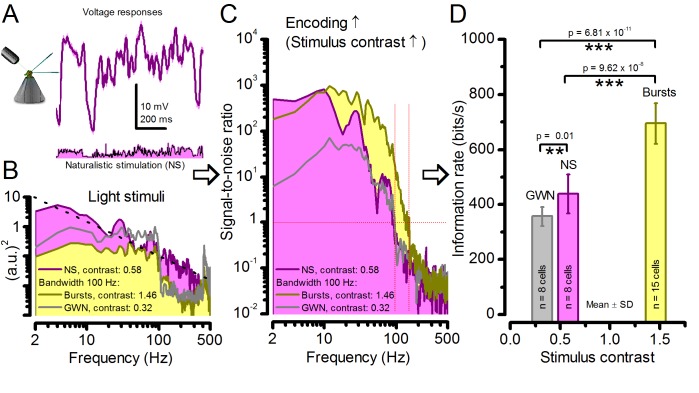
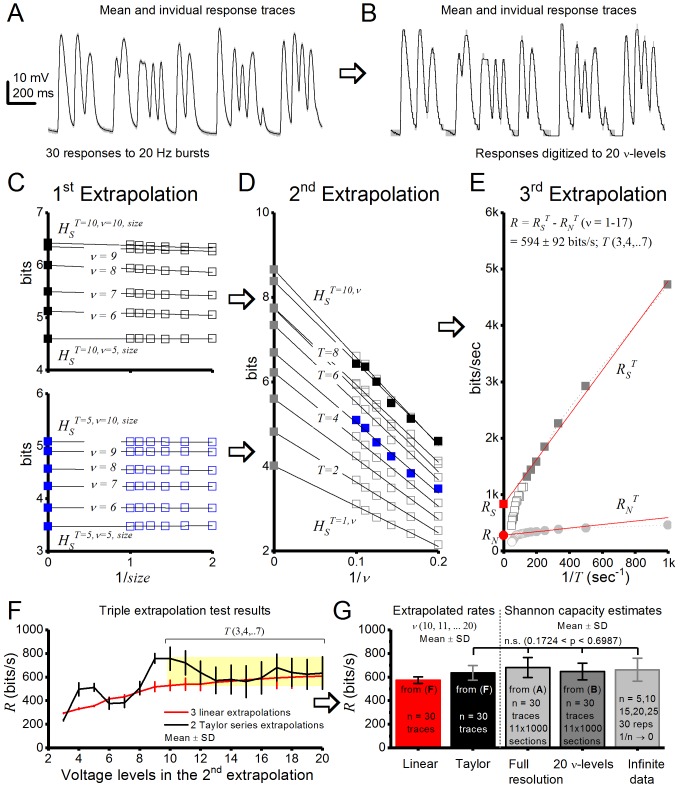
A R1-R6’s information transfer to high-frequency 100 Hz bursts exceeded 2-to-4-times the previous estimates. (A) Response signal-to-noise ratio (SNR, left) to 20 (red), 100 (yellow) and 500 Hz (blue) bursts, and to 50 Hz bandwidth stimuli of different contrasts (right); data from Figure 1. SNR increased with contrast (right), reaching the maximum (~6,000) for 20 Hz bursts (left, red) and the broadest frequency range for 100 Hz bursts (yellow). (B) Skewed bursts drove largely Gaussian responses (exception: 20 Hz bursts, red), with 100 Hz bursts evoking the broadest amplitude range (yellow). (C) Information transfer peaked for 100 Hz stimuli, irrespective of contrast (or BG; left), having the global maximum of ~850 bits/s (capacity, infomax) for the high-frequency high-contrast bursts. (D) Encoding efficiency, the ratio between input and output information (Routput/Rinput), was > 100% for 20 Hz bursts. Extra information came from the neighboring cells. Rinput at each BG was determined for the optimal mean light intensity, which maximized a biophysically realistic photoreceptor model’s information transfer (Appendix 2). Encoding efficiency fell with stimulus bandwidth but remained more constant with contrast. Population dynamics are in Figure 2—figure supplement 1.
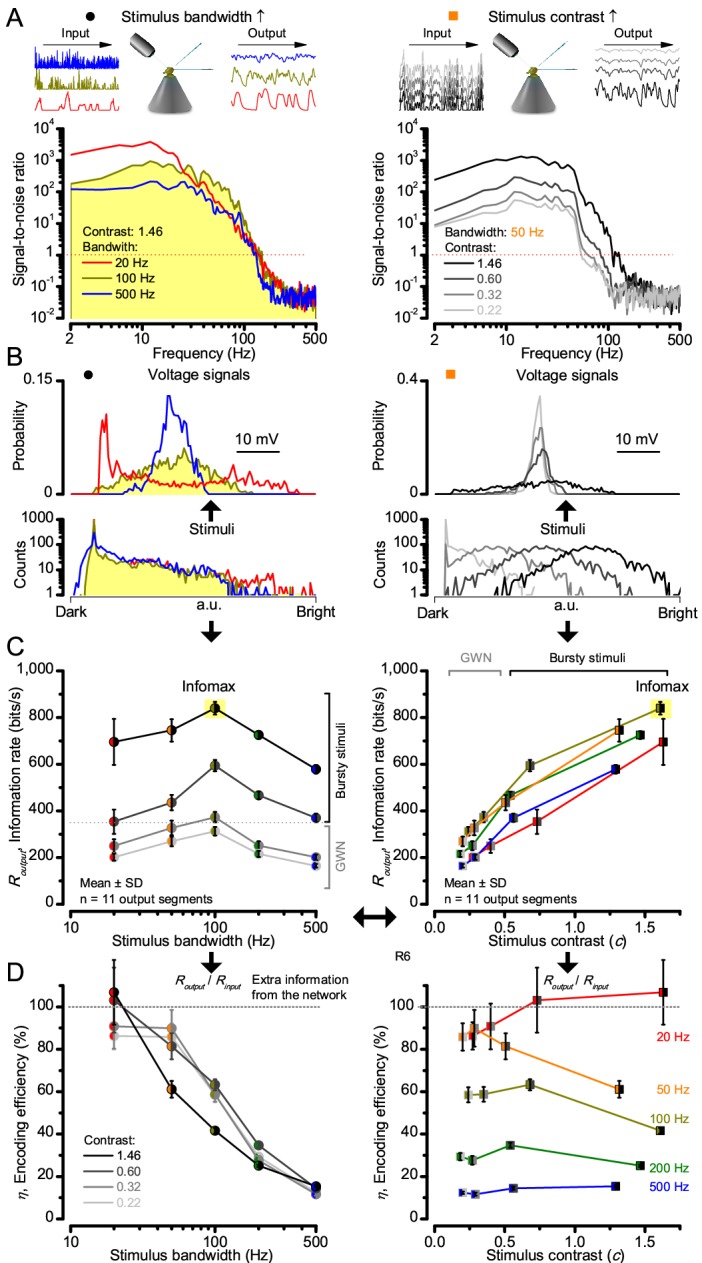
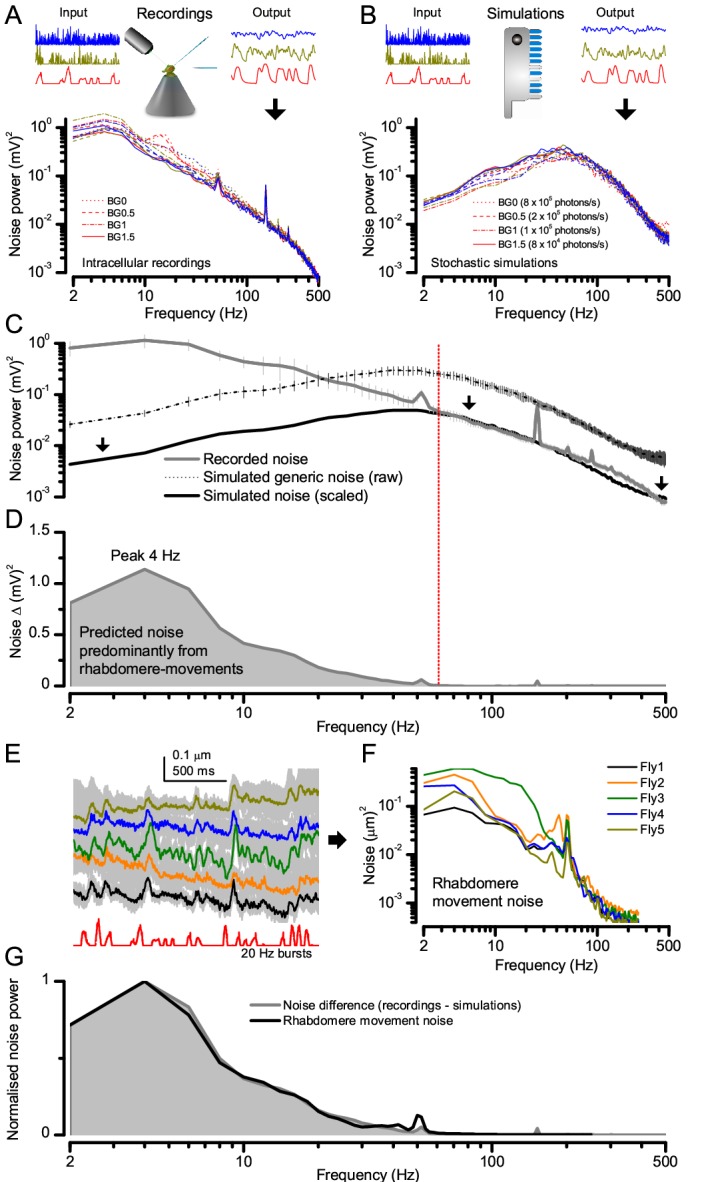
Figure 2—figure supplement 1. Signaling performance vary cell-to-cell but adapts similarly to given stimulus statistics.
(A) Response signal-to-noise ratios (SNR) to 20 (red), 100 (yellow) and 500 Hz (blue) bandwidth (left) saccadic bursts, and to 50 Hz bandwidth stimuli of different contrasts (right); color scheme as in Figure 1. SNR increases with contrast (right), reaching (in some cells)~6000 maximum for 20 Hz bursts (left, red). All R1-R6s showed the broadest frequency range for 100 Hz bursts (yellow). (B) Highly skewed bursts drove mostly Gaussian responses (exception: 20 Hz, red), with 100 Hz bursts evoking the broadest amplitude range (yellow). (C) Information transfer of all cells peaked for 100 Hz stimuli, irrespective of the tested contrast (or BG; left), having global maxima (infomax) between 600–850 bits/s (yellow box). (D) Mean encoding efficiency (Routput/Rinput) reached >100% for 20 Hz bursts, with its extra information coming from the neighboring cells. For determining Rinput see Figure 3. Encoding efficiency fell with increasing stimulus bandwidth, but less with contrast. Note: encoding efficiency for bursts (ηburst; black trace, left) was lower than for GWNs (ηGWN; grey and light grey traces). Because photomechanical adaptations let optimally 8-times brighter intensity modulation (photon absorption rate) through for high-contrast bursts (8 × 105 photons/s) than for GWN (1 × 105 photons/s), their input information is higher; . Thus, whilst , (Appendix 2).
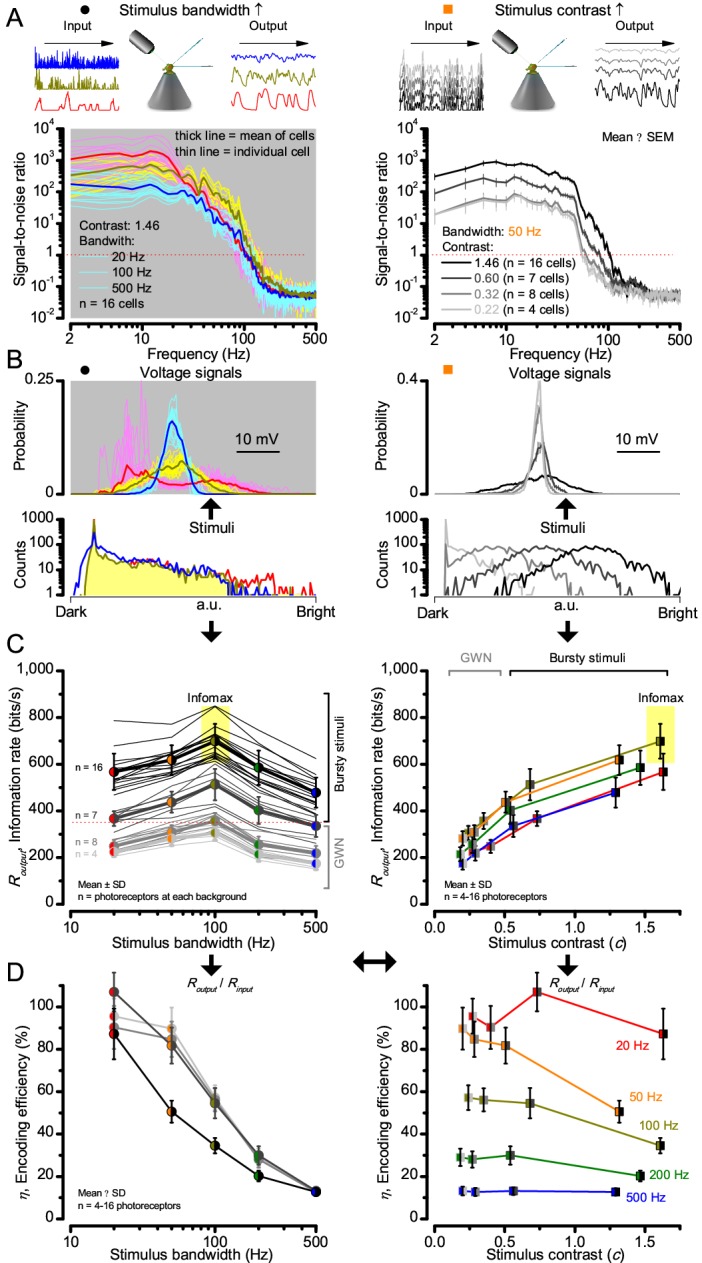
Figure 2—figure supplement 2. Light-adapted R1-R6 noise is similar for all the test stimuli, with its high-frequencies reflecting the mean quantum bump shape and its low-frequencies the rhabdomere jitter.
(A) Photoreceptor noise (from Figure 1) remained largely constant for all the test stimuli; extracted from the responses (output) to stimulus repetition (input); see Materials and methods. (B) Corresponding photoreceptor noise of the model (Song et al., 2012; Song and Juusola, 2014) simulations was also broadly constant but lacked the recordings’ low-frequency noise in (A). (C) The mean simulated noise power ascends with membrane impedance, which here was larger than that in the recordings in (A). Yet, the high-frequency parts of the real and simulated noise (>60 Hz), indicating the corresponding average light-adapted quantum bump waveform (Wong et al., 1982; Juusola and Hardie, 2001b; Juusola and Hardie, 2001a; Song et al., 2012; Song and Juusola, 2014), sloped similarly. (D) Overlaying these exposed the low-frequency noise difference (<60 Hz). Our results (Figure 8) predicted that this difference was a by-product of photomechanical rhabdomere and eye muscle movements, which the simulations lacked. (E) Mean rhabdomere movement responses (± SD, grey) in five different flies to the same repeated 20 Hz high-contrast bursts. These were smaller than those to 1 s flashing (Figure 8E, Appendix 7). (F) Average variability of the recording series (mean – individual response) shown as rhabdomere movement noise power spectra. (G) Mean rhabdomere movement noise (black trace; from F) matched its prediction (grey; from D). Therefore, the recordings’ extra noise resulted from variable rhabdomere contractions; jittering light input to R1-R6s. Crucially, this noise is minute; for 20 Hz saccadic bursts,~1/6,000 of R1-R6 signal power (Figure 2A).
Figure 2—figure supplement 3. Strong responses to naturalistic stimulation (NS) carry only about half the information of the strongest responses to bursts.
(A) The mean (signal; purple) and voltage responses (pink) of a R1-R6 photoreceptor to naturalistic light intensity time series. (B) At the light source, NS (purple), which is dominated by low-frequency transitions between darker and brighter events, had higher power than GWN (grey) or bursty high-contrast stimuli (yellow), but its mean contrast (0.58) is between the other two. (C) Signal-to-noise ratio of responses to NS has a similar low-frequency maximum to responses to bursty 100 Hz stimuli, but lower values at high-frequencies, similar to GWN-driven responses (grey). Both of these signaling performance estimates are from the same R1-R6 in (A). (D) Information transfer rate in photoreceptor output directly depends upon the mean stimulus contrast. Photoreceptors encode more information during naturalistic stimulation than during GWN stimulation (see also: Song and Juusola, 2014). But encoding can further double during high-contrast bursts, which utilize better the refractory sampling dynamics of 30,000 microvilli, generating the largest sampling rate changes. Significance by two-tailed t-test. For more explanation, see Appendix 3.
Figure 2—figure supplement 4. Drosophila R1-R6 photoreceptor output information transfer rate estimates to bursty stimuli are consistent.
Using triple extrapolation method to estimate entropy rate, RS, noise entropy rate, RN, and information transfer rate, R, of photoreceptor output to 20 Hz bursts. (A) Mean (black) and 30 voltage responses (light gray) of a photoreceptor to a 2-s-long bursty light intensity time series. (B), The responses were digitized to 2–20 voltage levels, ν; shown for 20 levels. Entropy, HS, and noise entropy HN, are calculated for T-letters-long words, in which each 1-ms-long letter is a voltage level, ν, as explained previously (Juusola and de Polavieja, 2003). (C) first extrapolation to infinite data size. Entropies of the 10 letter words (top) and five letter words (bottom) for 5–10 voltage levels fitted with linear trends. Thus, HSTT = 10,ν and HSTT = 5,ν (black and blue ■, respectively, for ν = 5–10) are obtained from extrapolation of HSTT = 10,ν,size and HSTT = 5,ν,size for size → ∞ (1/size → 0). Here, the probability of 5 letter words is similar for 50–100% of data so size corrections in HSTT = 5,ν are minute, but for 10 letter words size corrections impact HSTT = 10,ν slightly more. (D) second extrapolation to infinite voltage levels. HST,v is shown for words of 1–10 letters, each fitted with its linear trend. HST (gray ■s for T = 5–10) is obtained from the extrapolation of HST,v when ν → ∞ (1/ν → 0); HST = 5 = blue ■; HST = 10 = black ■. (E) third extrapolation. Entropy rates obtained from extrapolations to infinitely long words. The total entropy rate, RS (red ■), is obtained from a linear extrapolation when T → ∞ (1/T → 0). RN (red ●) for the same data. Both RS and RN collapse to 0 when the data are inadequate to provide a satisfactory extrapolation of HST and HNT for long words and high voltage resolutions. The graph, however, shows enough linearly aligned points for good estimations of RS, RN, and R. (F) Effect of the number of voltage levels v used in the second extrapolation on R. For v ≥ 8, the first point for the second extrapolation is the fifth voltage level. Linear fits (red) and second-order Taylor series (black) give similar estimates (<10% difference) when v = 10–20 for these data. (G) Average R estimates obtained from linear (red) or second-order Taylor series (black) fits by the triple extrapolation method (Eq. 4) and from Shannon equation (Eq. 1). These estimates for data in (A) are similar. For 20 voltage level data (B), the mean Shannon capacity estimate is only ∼2–5% less than the mean estimates for the full response waveforms with n = 30 trials or when extrapolated to infinite data (1/n → 0), implying consistency in these estimation methods.