Fig. 4.

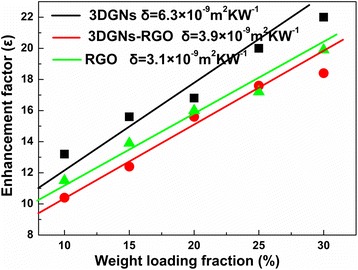
Calculated thermal boundary resistance of the various samples. Thermal boundary resistance (δ) is an important parameter to determine the resulting thermal performances of TIMs. Based on Balandin’s theory, thermal conductivity of graphene-modified ER is closely related to the value of the δ. After calculation, the similar δ values of the RGO-ER and RGO-3DGNs-ER samples prove that the added RGO nanosheets are loaded on the surface of the 3DGNs (Fig. 4). Based on our previous findings, the δ value of the 3DGNs-ER sample is much higher that of the RGO-ER because of the poor contact between the 3DGNs and ER. The functional groups of the RGO nanosheets bring about a better contact at the interface, which leads to the smaller δ compared with that of 3DGNs-ER sample