Ultrahigh mobility and efficient charge injection in monolayer organic thin-film transistors on boron nitride

An ultimate monolayer of 2D organic crystal can deliver high OTFT performance and be a clean system to investigate device physics.

Abstract

Organic thin-film transistors (OTFTs) with high mobility and low contact resistance have been actively pursued as building blocks for low-cost organic electronics. In conventional solution-processed or vacuum-deposited OTFTs, due to interfacial defects and traps, the organic film has to reach a certain thickness for efficient charge transport. Using an ultimate monolayer of 2,7-dioctyl[1]benzothieno[3,2-b][1]benzothiophene (C₈-BTBT) molecules as an OTFT channel, we demonstrate remarkable electrical characteristics, including intrinsic hole mobility over 30 cm²/Vs, Ohmic contact with 100 Ω · cm resistance, and band-like transport down to 150 K. Compared to conventional OTFTs, the main advantage of a monolayer channel is the direct, nondisruptive contact between the charge transport layer and metal leads, a feature that is vital for achieving low contact resistance and current saturation voltage. On the other hand, bilayer and thicker C₈-BTBT OTFTs exhibit strong Schottky contact and much higher contact resistance but can be improved by inserting a doped graphene buffer layer. Our results suggest that highly crystalline molecular monolayers are promising form factors to build high-performance OTFTs and investigate device physics. They also allow us to precisely model how the molecular packing changes the transport and contact properties.

INTRODUCTION

OTFTs serve as the fundamental building blocks for many organic electronic applications, such as the backplane of flat-panel displays and flexible circuits (1–3). These applications demand high carrier mobility, low-voltage operation, and long operational stability. In recent years, by inventing new materials (4, 5), optimizing molecular packing or interfacial properties (6, 7), and invoking new processing methods (8–10), the mobility of OTFTs has exceeded 10 cm²/Vs for both holes and electrons (8, 11, 12), on par with polycrystalline silicon and organic single crystals. However, even these state-of-the-art OTFTs are often limited by contacts, as reflected by low mobility in the linear regime, strong nonlinearity in the current-voltage characteristics, and large bias voltage (tens of volts) to achieve current saturation (8, 13). In the commonly used bottom-gate, top-contact geometry, a significant contribution of contact resistance comes from vertical transport through the film, leading to typical contact resistance ranging from 10³ to 10⁶ Ω · cm (14, 15). Large V_ds may also cause potential stability issues because it facilitates the migration of trapped charges (16) and generates excess heat during device operation.

A possible route to build high-performance and low-voltage OTFTs is to use two-dimensional (2D) ultrathin film as a channel, where the metal leads are in direct contact with the accumulation layer (17–23). Similar to 2D atomic crystals (24), this form factor should have advantages in channel electrostatics, power consumption, and device downscaling over the bulk thin film while still maintaining high mobility. Recently, Jiang et al. demonstrated monolayer 1,4-bis((5′-hexyl-2,2′-bithiophen-5-yl)ethynyl) benzene OTFT by cast assembly method (25). Solution epitaxy and floating-coffee-ring–driven assembly have also been developed to grow and transfer 2D crystals of various organic semiconductors up to centimeter size, with mobility on the order of several square centimeters per volt-second (17, 21). He et al. demonstrated the van der Waals (vdW) epitaxy of few-layer C₈-BTBT on graphene and boron nitride (BN), with extrinsic mobility up to 10 cm²/Vs (19). So far, however, the device physics of monolayer OTFTs (including intrinsic transport and contact properties) and device optimizations have not been explored. In terms of the mobility and contact resistance, the potential of 2D OTFTs has not been fully revealed.

Here, taking C₈-BTBT as an example, we investigate the intrinsic mobility and contact properties of crystalline monolayer OTFTs. We show that it is possible to deliver state-of-the-art high-performance OTFTs with just a monolayer channel. Compared to thin films or single crystals, the main advantage lies in the direct contact with the charge transport layer, leading to extremely low parasitic resistance, while maintaining the intrinsic mobility of bulk crystals. Counterintuitively, we observe exponentially large contact resistance with strong nonlinear current-voltage characteristics in bilayer and thicker devices due to the increased Schottky barrier (SB) width that suppresses tunneling. This Schottky contact has also been commonly observed in solution-processed C₈-BTBT OTFTs (8, 13). By inserting a doped graphene between the channel and metal leads, the contact resistance is significantly reduced, and the linear output characteristics are restored. Density functional theory (DFT) calculations reveal that the density of states (DOSs) at the Fermi energy, which is modulated by the molecular packing, plays important roles in the contact and transport properties. Our results demonstrate the promise of crystalline monolayer organic semiconductors as building blocks for high-performance and low-power OTFTs and as clean systems for studying device physics.

RESULTS AND DISCUSSION

Monolayer C₈-BTBT OTFTs

Following our previous studies (19, 26), low-temperature vdW epitaxy of highly crystalline and uniform C₈-BTBT was carried out in a vacuum tube furnace on exfoliated BN (fig. S1A). Because of the competition between intra- and interlayer vdW interactions, the interfacial layer (IL; insulating) and the first layer (1L) have different molecular packing from bulk crystals; in contrast to IL and 1L, bulk-crystal molecular packing is restored from the second layer (2L) with a height of ~3 nm (19). After growth, we carefully laminated prepatterned Au electrodes on the C₈-BTBT films as electrical contacts of back-gated OTFTs (see Methods for the detailed device fabrication process). The nondestructive transfer process well preserved the integrity of the molecular packing down to the monolayer limit, as shown by the cartoon and cross-sectional transmission electron microscopy (TEM) image of the Au/C₈-BTBT/BN stack (Fig. 1, A and B). Remarkably, both interfaces were atomically flat without trapped impurities over large area. Note that because the IL is insulating (19), we do not explicitly count this layer throughout this paper.

Fig. 1. Device geometry of monolayer C₈-BTBT OTFT and its electrical characteristics.

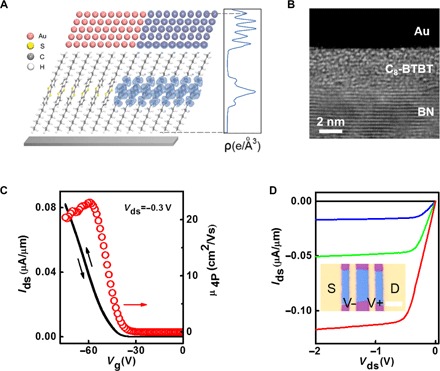
(A) Schematic illustration of the contact between Au and C₈-BTBT. The right part is overlaid by the charge density in the energy range of [E_F-0.5 eV, E_F]. E_F is the Fermi energy of the system. The distribution of charge density along the z direction is plotted. (B) Cross-sectional TEM image of Au/C₈-BTBT/BN stack, showing atomically smooth interface. (C) Room temperature double-sweep I_ds-V_g characteristics (black line) and the extracted four-terminal field-effect mobility as a function of V_g (red circle). (D) I_ds-V_ds characteristics of the same device in (C). From top to bottom, V_g = −20, −50, −60, and −70 V, respectively. Inset shows the microscopic image of the device. The source (S), drain (D), and voltage probes (V−, V+) are marked. Scale bar, 6 μm.

Let us first focus on monolayer C₈-BTBT OTFTs. Figure 1 (C and D) displays the room temperature transfer (I_ds-V_g) and output (I_ds-V_ds) characteristics of a representative 1L C₈-BTBT device with 18-μm channel length (see figs. S2 and S3 for additional devices). Several remarkable features were observed in spite of the monolayer channel thickness: extrinsic field-effect mobility μ_2P of ~5 to 10 cm²/Vs (fig. S2C), on/off ratio of >10⁷, excellent linearity in both transfer and output characteristics, and negligible hysteresis. Another unique feature was the nearly complete current saturation around V_ds = −0.5 V in the output characteristics (Fig. 1D), which was two orders of magnitude lower than solution-processed C₈-BTBT OTFTs (8, 13, 27). The saturation current density of 0.1 to 0.15 μA/μm was similar to the C₈-BTBT OTFTs by off-center spin-coating method (8) but was lower than the printed or doped ones (13, 27). Nevertheless, our devices consumed significantly lower power (or drive voltage) to deliver similar saturation current density. There are two commonly accepted mechanisms for current saturation in field-effect transistors (FETs): channel pinch-off due to the depletion of carriers at the drain side and velocity saturation. We can rule out the former because the devices repeatedly show current saturation at extremely small V_ds ~ 1 V, where the channel was far away from pinch-off (|V_g| − |V_th| ≫ |V_ds|). Therefore, we attribute the current saturation to velocity saturation. Because the vertical electric field in our devices is much larger than the lateral field, we can extract the carrier velocity from the output characteristics using the gradual channel approximation (28), as shown in fig. S2D. The nearly linear field dependence at low field is consistent with a constant mobility of 10 cm²/Vs. However, at a lateral field of ~1000 V/cm, the velocity reaches saturation of about 1.1 × 10⁴ cm/s, close to the reported values for organic FET at room temperature (28, 29). It is well known that the charge transport in organic semiconductors is more strongly coupled to molecular vibrations, including intra- and intermolecular vibrational modes, to form the so-called polarons. The electron-phonon coupling can be comparable to electronic coupling rather than playing a perturbative role in the charge transport as in their inorganic counterparts (30). Furthermore, the large effective mass from the small band dispersion will also reduce the saturation velocity.

To further investigate the intrinsic mobility and contact properties of monolayer OTFTs, we designed and transferred four Au electrodes across the channel (Fig. 1D, inset) and performed gated four-point probe (gFPP) measurements. By passing a current I_ds through the source and drain electrodes and simultaneously measuring the voltage drop (ΔV) between the two probes separated by D, intrinsic mobility, ${\mathrm{\mu }}_{4\mathrm{P}}=\left(\frac{\mathit{D}}{\mathrm{W}{\mathit{C}}_{\mathrm{i}}\mathrm{\Delta }\mathrm{V}}\right)\left(\frac{\mathit{d}{\mathit{I}}_{\text{ds}}}{\mathit{d}{\mathit{V}}_{\mathrm{g}}}\right)$, and contact resistance, ${\mathit{R}}_{\mathrm{c}}=(\frac{{\mathit{V}}_{\text{ds}}}{{\mathit{I}}_{\text{ds}}}-(\frac{\mathit{L}}{\mathit{D}}\left)\right(\frac{\mathrm{\Delta }\mathit{V}}{{\mathit{I}}_{\text{ds}}}\left)\right),$ were extracted as a function of temperature and V_g (31). Here, we used the spacing between the inner edges of the voltage probes as D, so μ_4P was the conservative lower bound. There are several requirements to minimize the errors in gFPP: (i) The devices are operated in the linear regime so that the gradual channel approximation holds (15), and (ii) the contact must be Ohmic with low resistance. Therefore, this technique is suitable for monolayer C₈-BTBT devices (but not for bilayer and thicker ones, as will be discussed later).

Using gFPP, we found that the intrinsic mobility (in the linear regime) was 23 cm²/Vs for the device in Fig. 1. Figure 2 presents the gFPP measurement results of the same device down to 60 K. At on state, the channel conductance ${\mathrm{\sigma }}_{4\mathrm{P}}=\frac{{\mathit{I}}_{\text{ds}}}{\mathrm{\Delta }\mathit{V}}$ was nearly linear with V_g without obvious kinks, so the contact-induced mobility overestimation was unlikely (32). For this particular device, μ_4P was about four times higher than μ_2P (Fig. 2A). Statistical analysis over 12 monolayer devices showed that the average room temperature intrinsic mobility was 24.5 cm²/Vs, and the best device exceeded 30 cm²/Vs (Fig. 2C). Despite having only monolayer conducting channel, the mobility is among the highest reported to date for OTFTs (8, 33). Furthermore, the monolayer C₈-BTBT exhibited clear band-like transport until ~150 K, evidenced by the increase of σ_4P and μ_4P upon cooling, as well as the higher average mobility at lower temperatures (Fig. 2, A to C, and fig. S3).

Fig. 2. Temperature-dependent electrical transport of the monolayer C₈-BTBT OTFT in Fig. 1.

(A) Channel conductance σ_4P as a function of V_g under different temperatures. (B) Extrinsic and intrinsic mobility as a function of temperature. (C) Histogram of the intrinsic mobility of monolayer devices at different temperature. During the cooling process, some devices were broken, so the number of devices decreases at low temperature. (D) Low-bias I_ds-V_ds characteristics at V_g = −70 V under T = 300 K (red), 200 K (blue), 100 K (green), and 80 K (black). Inset shows the contact resistance at V_g = −70 V as a function of temperature, derived from the gFPP measurements.

Contact resistance is another important aspect in OTFTs. Realization of low-resistance Ohmic contact not only increases the extrinsic speed of the transistors but also reduces the voltage and power consumption. From the gFPP measurements, we readily deduced that the on-state contact resistance of monolayer devices was typically in the range of 100 to 400 Ω · cm (Fig. 2D and fig. S4). In conventional OTFTs, there are many approaches to optimizing contact resistance, including inserting a dopant layer at the contact interface, tuning the contact metal work function by a self-assembled monolayer, optimizing band alignment between the organic semiconductor and contact material, and optimizing the device fabrication process; but only a few studies have reported contact resistance below 1 kΩ · cm. In particular, Darmawan et al. (34) reduced the contact resistance of C₈-BTBT OTFT to 0.2 kΩ · cm by introducing FeCl₃ as a dopant layer. Uemura et al. (35) reached the contact resistance below 0.2 kΩ · cm in C₁₀DNTT (2,9-didecyldinaphtho[2,3-b:2′,3′-f]thieno[3,2-b]thiophene) top contact OTFT by annealing process. Hulea et al. (36) reported contact resistance as low as 0.1 kΩ · cm in rubrene single-crystal FET by nickel contacts. We can see that the contact resistance of our 1L OTFT is among the lowest values in OTFTs due to direct and noninvasive contact with the charge transport layer (14). The low-bias output characteristics were exceptionally linear and temperature-insensitive down to ~100 K (Fig. 2D and fig. S3B), indicating that the contact was Ohmic and almost barrierless. This happened when the barrier was thin or leaky enough that the carrier injection was through quantum mechanical tunneling process (37). Considering that the hole-transporting molecular states were mainly distributed in the benzothiophene core (13), we attributed the tunneling barrier to the length of the side carbon chain (~0.72 nm), separating Au from the benzothiophene core of 1L C8-BTBT (Fig. 1A). This intimate and nondestructive contact to the transport layer (Fig. 1B) probably represents the ultimate limit in terms of the carrier injection efficiency.

Few-layer C8-BTBT OTFTs

We further fabricated few-layer C₈-BTBT OTFTs (up to seven layers) and performed thickness-dependent studies. Figure 3A plots the typical I_ds-V_ds characteristics of monolayer to trilayer OTFTs. The bilayer and trilayer devices showed strong nonlinearity at low V_ds, in clear contrast with monolayer devices. The low-bias resistance in bilayer and trilayer devices was completely dominated by contacts, which was about two and four orders of magnitude higher than that of the monolayer device, respectively. The Schottky contact was further confirmed by the thermally activated behavior at low temperature (Fig. 3B). Quantitatively, the low-bias current can be modeled by thermionic emission over a 2D channel (38, 39), ${\mathit{I}}_{\text{ds}}\propto {\mathit{T}}^{3/2} \text{exp}(-\frac{\mathit{q}{\mathrm{\Phi }}_{\mathrm{B}}}{{\mathit{k}}_{\mathrm{B}}\mathit{T}})$, where Φ_B is the SB height, k_B is the Boltzmann constant, T is the temperature, and q is the electronic charge. From the linear fitting of the Arrhenius plot (Fig. 3C), we derived Φ_B under different V_g, which showed two regimes separated by the flat-band voltage (Fig. 3D, arrow). Below the flat-band voltage, Φ_B had a linear dependence on V_g because thermionic emission was dominant. At the flat-band voltage, thermally assisted tunneling became relevant, and Φ_B started to deviate from the linear trend (40). The true SB height, defined as the Φ_B in the flat-band condition, was extracted to be 140 meV (Fig. 3D). In fig. S5, another bilayer device had a similar SB height of 170 meV. We note that the SB lowering due to image force is on the order of several millielectron volts, which is insignificant compared to the SB height.

Fig. 3. Thickness-dependent OTFT properties.

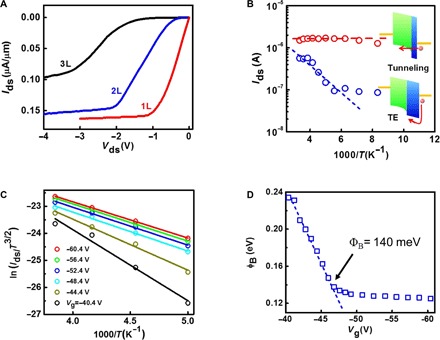
(A) Room temperature I_ds-V_ds characteristics for typical monolayer, bilayer, and trilayer devices. (B) Arrhenius plot of I_ds (V_g = −70 V, V_ds = −1 V) of the monolayer (red circle) and bilayer (blue circle) devices in (A). The inset shows energy band diagrams near the contact, with different mechanisms. (C) Arrhenius plot of ln(I_ds/T^3/2) of the bilayer device in (A). From top to bottom: V_g = −60.4, −56.4, −52.4, −48.4, −44.4, and −40.4 V. (D) Derived SB height as a function of V_g. The true SB height is 140 meV, as pointed by the arrow.

The distinctive contact behavior in monolayer and bilayer C₈-BTBT OTFTs was most likely modulated by the SB width (Fig. 3B, inset). We speculated that in bilayer devices, due to the greater physical separation (~3 nm) between the Au metal and the charge-transporting 1L, the SB width was much larger. As a result, tunneling current was suppressed, and thermionic emission over the barrier became the dominant mechanism. Our speculation was supported by the much larger contact resistance and stronger nonlinearity in trilayer C₈-BTBT devices, where the SB was even thicker (Fig. 3A). Our model does not include tunneling current through the SB, which is important to accurately describe the electrical characteristics of ultrathin body SB-FETs (41). Therefore, the SB height is only an estimation. From the above analysis and the strong output nonlinearity, however, we believe that the tunneling only plays minor roles in our few-layer C₈-BTBT OTFTs at on state, likely due to the limited gate voltage. However, we were not able to perform the quantitative temperature-dependent analysis on trilayer devices because the low-bias I_ds was below the detection limit at low temperature.

Electronic and contact properties of C₈-BTBT by DFT calculations

The well-defined C₈-BTBT/Au interface allows us to perform advanced DFT calculations on the electronic and contact properties (see Methods and figs. S6 to S11 for details) and correlates with experiments. This has been very difficult in conventional OTFTs because of highly disturbed packing structure at the organic-metal interface by metal diffusion (14). We first determined the structure of 1L and 2L C₈-BTBT by surveying a wide range of the initial tilting angle from 30° to 90° along the [010] direction of the bulk crystal and by allowing the structures to fully relax (fig. S6). The two most energetically preferred tilting angles, that is, ~60° and 90°, correspond to 1L and 2L, respectively (fig. S6). This assignment was qualitatively consistent with the reduced thickness in 1L due to the molecule-substrate interactions (19, 26). When C₈-BTBT molecules stack together to form crystalline layers, each original molecular orbital [for example, highest occupied molecular orbital (HOMO) or HOMO-1] (fig. S7) evolves into two electronic bands because the unit cell consists of two molecules. The calculated bandgap for 1L and 2L C₈-BTBT is 2.57 and 2.03 eV, respectively (fig. S8). For 1L, the highest valence states responsible for the hole transport (1LVB1 and 1LVB2) are nearly degenerate at the G point and have weak band dispersion, leading to high DOS below the valence band maximum (VBM) (Fig. 4, A and B). On the other hand, the highest valence state of 2L (that is, 2LVB1) has a rather strong band dispersion and low DOS. Figure 4 (C and D) visualizes the molecular orbitals of these states, showing that 1LVB1 and 1LVB2 are both delocalized with significant intermolecular overlap and high expected mobility. However, 2LVB1 is a localized (nonbonding) state at the G point but transforms to a bonding state along the G-X direction of the Brillouin zone, roughly at 0.27 eV below the VBM (Fig. 4D and figs. S8B and S9). The difference between the molecular orbitals in 1L and 2L is modulated by their molecular packing. The two highest VBs are formed through intermolecular S-S and S-C interactions in both 1L and 2L. The strengths of both interactions are comparable in 1L, leading to the nearly degenerated 1LVB1 and 1LVB2 at the G point. The stand-up packing of 2L, however, forces the two S 3p orbitals of adjacent molecules approaching each other in an improper direction (see fig. S10 for a detailed explanation). This substantially less favored S-S interaction causes the localization of 2LVB1 and moves 2LVB2 energetically, ~0.5 eV higher at the G point.

Fig. 4. Calculated electronic and contact properties.

(A) Band alignment of Au/1L and Au/2L metal-semiconductor junction. Four valance states responsible for the hole transport are marked (the band structure is shown in fig. S8). The color of these states indicates different DOSs as shown by the color bar. (B) Total DOS for 1L (blue solid line) and 2L C₈-BTBT (red solid line). Blue and red arrows mark the highest-energy valence bands for 1L and 2L, respectively. (C) Spatial distribution of the molecular orbitals at G point for 1LVB1 and 1LVB2. (D) Spatial distribution of the molecular orbitals at G and X point (0.5, 0, 0) for 2LVB1 using an isosurface of 0.0005 e bohr⁻³.

To build the electrical contact and calculate its properties, we added a six-layer Au (111) slab on the C₈-BTBT layer and allowed the structure to fully relax (fig. S11). Figure 4A illustrates the calculated band alignment of several highest valence states (at the G point) of 1L and 2L C₈-BTBT with the Fermi energy of Au (E_F). The nearly perfect alignment of 1LVB1 and 1LVB2 with E_F well explains the barrierless Ohmic contact in 1L C₈-BTBT OTFTs. The quantum mechanical tunneling probability at the Au/C₈-BTBT interface is proportional to the number of conducting channels (that is, the DOS). Thus, the enhanced DOS near the 1L VBM further increases the tunneling probability and decreases the contact resistance. For 2L, although 2LVB1 aligns with E_F very well, it comes with a low DOS. In addition, because 2LVB1 is localized at bias voltage, it effectively acts as an impurity band to absorb the injected carriers (Fermi level pinning) and lead to the large SB height observed experimentally. The next available valence state, 2LVB2, has a much larger energy barrier of ~0.5 eV (Fig. 4A). Quantum confinement plays an important role in the electronic transport of devices composed of some 2D atomic crystals (42) and quantum dots (43). The size reduction in one or more dimensions usually enhances the bandgap, accompanied with the shift of positions of conduction or valence bands (for example, in black phosphorus) (42, 44). However, for 2D C₈-BTBT, the organic layers are stacked with extremely weak interlayer coupling through alkyl chains, leading to nearly vanished electronic band dispersion along the out-of-plane direction. In addition, the height of each C₈-BTBT layer is ~3 nm, several times that of common 2D atomic crystals, which weakens the confinement by many times, if they exist at all. In our theoretical calculations, the quantum size effect (owing to thickness confinement) is fully considered when we used one and two organic layers to model the 1L and 2L with substantial vacuum layers.

Contact optimization by doped graphene layer

To further optimize the contact of bilayer devices, we inserted chemical vapor deposition (CVD) graphene as a buffer layer at the Au/C₈-BTBT interface (Fig. 5, A and B; see Methods for fabrication process). Previous studies have shown that, compared to metals, graphene can improve the contact properties of many organic and 2D semiconductors due to its tunable work function, clean interface, and more intimate contact with vdW materials (45, 46). Before making the graphene/Au contact stack, we performed a brief ultraviolet (UV)/ozone (UVO) treatment on graphene, which was vital to the contact improvement. First, the UVO could remove the polymethyl methacrylate (PMMA) residue from the transfer process and make the graphene surface cleaner (Fig. 5C and fig. S12, A to E). Second and more importantly, it introduced controlled p-doping by oxygen absorption (47, 48). The doping was confirmed by the evolution of the Raman spectra with the UVO time (fig. S12, F and G). We found that 20-min treatment was the optimal condition to maintain the continuity of graphene while introducing the maximum hole doping (fig. S12) (49). We note that longer UVO time would make the graphene discontinuous, leading to adverse effects as an electrical contact.

Fig. 5. Electrical characteristics of graphene-contacted bilayer C₈-BTBT OTFT.

(A) Schematic illustration of the device geometry. (B) Cross-sectional TEM image of Au/graphene/C₈-BTBT/BN stack. The arrows point at the position of graphene. (C) Raman spectra and AFM (inset) of CVD graphene undergone 20-min UVO treatment. Several characteristic peaks are marked. Scale bar, 3 μm. (D) Room temperature double-sweep I_ds-V_g characteristics of a typical graphene-contacted bilayer device. (E) Room temperature I_ds-V_ds characteristics of the same device in (D). From top to bottom, V_g = −20, −50, −60, and −70 V.

With doped graphene/Au stack as the contact, the nonlinear output characteristics of bilayer OTFTs were largely eliminated (Fig. 5, D and E). Low-temperature electrical measurements revealed that the SB height was reduced by ~0.1 eV compared to bare Au contact (fig. S13), consistent with the linear output characteristics. Similar reduction of SB was observed in MoS₂/graphene contact (46, 50). The extrinsic mobility of the graphene-contacted bilayer devices was 2 to 4 cm²/Vs at room temperature, lower than that of the 1L devices. From the low-temperature behavior, it was clear that the contact of Au/graphene/2L-C₈-BTBT, although improved over the bare Au, was less ideal than the monolayer devices. Therefore, the contact resistance was higher in the former. On the other hand, the initial increase of current upon cooling (fig. S13C) did indicate band-like transport in bilayer C₈-BTBT. Unfortunately, we were not able to transfer four-probe electrodes with graphene/Au due to technical difficulties; thus, the contact resistance and intrinsic mobility of bilayer devices remain to be investigated. Nevertheless, comparison of Figs. 3 and 5 demonstrates the significant improvement of contact using graphene.

CONCLUSION

In conclusion, we demonstrate that it is possible to build the best OTFT with an ultimate monolayer of organic molecules, provided that the molecular packing, interface settings, and electrical contact are collectively optimized. By preserving the pristine molecular structure at semiconductor/dielectric and semiconductor/metal interfaces, the performance of our monolayer C₈-BTBT OTFTs excels in all key aspects including mobility, contact resistance, and power consumption. Direct, intimate contact with the charge-transporting layer enables the extremely low contact resistance and saturation voltage, which has been very difficult for conventional OTFTs. The results, although somewhat surprising, are consistent with the highly anisotropic nature of C₈-BTBT and many other organic semiconductors, where the in-plane transport has much higher mobility than the out-of-plane transport. In these cases, the best strategy is to avoid the vertical path as much as possible and contact the transport layer directly. Furthermore, the clean interface offers new opportunities to explore the insights of the molecular configurations and interface structures in relation to the device performance. Given the recently developed large-area solution synthesis and transfer techniques (17, 21), 2D organic semiconductors could find potential applications in commercial organic electronics.

METHODS

Growth and characterization of C₈-BTBT

The monolayer to few-layer C₈-BTBT was grown on exfoliated BN following earlier works (19, 26). We used atomic force microscopy (AFM) (Asylum Cypher) to measure the BN flakes before and after growth to obtain the accurate thickness of C₈-BTBT. We only selected uniform C₈-BTBT films over the micrometer scale to further fabricate OTFTs.

Cross-sectional TEM specimens were prepared using the standard focused ion beam lift-out process on an FEI Quanta 3D dual beam microscopy. TEM images were obtained on an FEI Tecnai F20 microscopy operated at an acceleration voltage of 200 kV.

OTFT fabrication and measurements

For two-probe devices with Au contact, we used TEM grid as shadow mask to deposit 200 μm × 80 μm Au patches on a 285-nm SiO₂/Si substrate. The thickness of the Au patches was 100 nm. Two patches were picked up and transferred onto the C₈-BTBT sequentially as source/drain contact electrodes. The details of the transfer process were described by Zhang et al. (23).

For four-probe devices with Au contact, we first deposited 1 cm × 1 cm Au film with 100-nm thickness on the SiO₂/Si substrate. We then used photolithography and wet etching (Gold Etchants TFA, Transene Company Inc.) to pattern the Au film into four-probe electrode configuration. We transferred the source, drain, and voltage probes sequentially to finish the fabrication of the four-probe device. During the transfer, great care was taken to align the electrodes into the desirable position.

For two-probe devices with graphene contact, the fabrication process was similar, except that the Au was deposited on doped CVD graphene on the SiO₂/Si substrate. The graphene was synthesized in a tube furnace at a temperature of 1035°C on copper foils (Alfa Aesar). After growth, graphene was transferred onto 285-nm SiO₂/Si substrate using PMMA as supporting layer, followed by acetone soaking overnight. We then exposed the graphene in a custom-built UVO setup to remove the PMMA residues and introduce p-doping. The graphene was characterized by AFM and Raman spectroscopy (Horiba HR800 confocal Raman microscope). All electrical measurements were carried out by an Agilent B1500 semiconductor parameter analyzer in a closed-cycle cryogenic probe station with a base pressure of 10⁻⁵ torr.

Details of DFT calculations

DFT calculations were performed using the generalized gradient approximation for the exchange-correlation potential, the projector augmented wave method (51), and a plane-wave basis set as implemented in the Vienna ab initio simulation package (52). In all calculations, vdW interactions were considered in the framework of vdW-DF with the optB88 functional for the exchange energy (optB88-vdW) (53, 54), which was found suitable for modeling geometric and electronic properties in 2D materials (23, 44, 55–57). The energy cutoff for the plane-wave basis was set to 600 eV in the simulation of 1L and 2L C₈-BTBT. and was set to 400 eV for Au–C₈-BTBT junctions. Two k-meshes of 8 × 6 × 1 and 6 × 4 × 1 were used to sample the Brillouin zone of C₈-BTBT layers for geometric and electronic structure calculations, respectively. The vacuum region is ~30 Å in thickness. The shape and volume of C8-BTBT layers were fully relaxed until the residual force per atom was less than 0.01 eV/Å. In terms of Au–C₈-BTBT junctions, a 1 × 2 C₈-BTBT supercell with a vacuum layer of ~20Å was used and the lattice constants were kept as those of 1L and 2L C₈-BTBT, respectively. A k-mesh of 6 × 2 × 1 was used to sample the Brillouin zone. For Au–C₈-BTBT junctions, the shape and volume of the supercell and all Au Atoms were kept fixed. All other atoms in the junctions were fully relaxed until the residual force per atom was less than 0.02 eV/Å.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/9/e1701186/DC1

fig. S1. AFM images of several representative C₈-BTBT thin films on BN with different thickness.

fig. S2. A two-terminal monolayer C₈-BTBT OTFT.

fig. S3. Electrical data of another four-probe monolayer C₈-BTBT OTFT.

fig. S4. Histogram of contact resistance of 12 monolayer C₈-BTBT OTFTs.

fig. S5. Electrical data of another bilayer C₈-BTBT OTFT.

fig. S6. We investigated 14 configurations through rotating β and θ angle of C₈-BTBT molecules from 90° to 30° along the x and y axis, respectively.

fig. S7. Geometric structure of single C₈-BTBT molecule and visualized wave functions.

fig. S8. Electronic band structures of 1L and 2L C₈-BTBT.

fig. S9. Visualized wave functions for six states in the momentum space of the highest valence band of 2L C₈-BTBT.

fig. S10. Visualized G-point wave functions for VB1 and VB2 of 1L and 2L in yz and xy (top view of thiophene part) planes, respectively.

fig. S11. The contact models of Au electrodes with 1L or 2L C₈-BTBT.

fig. S12. Characterizations of CVD graphene.

fig. S13. Electrical data of another graphene-contacted bilayer C₈-BTBT OTFT.