Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2017 Sep 6;7:10717. doi: 10.1038/s41598-017-11125-z

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2017

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

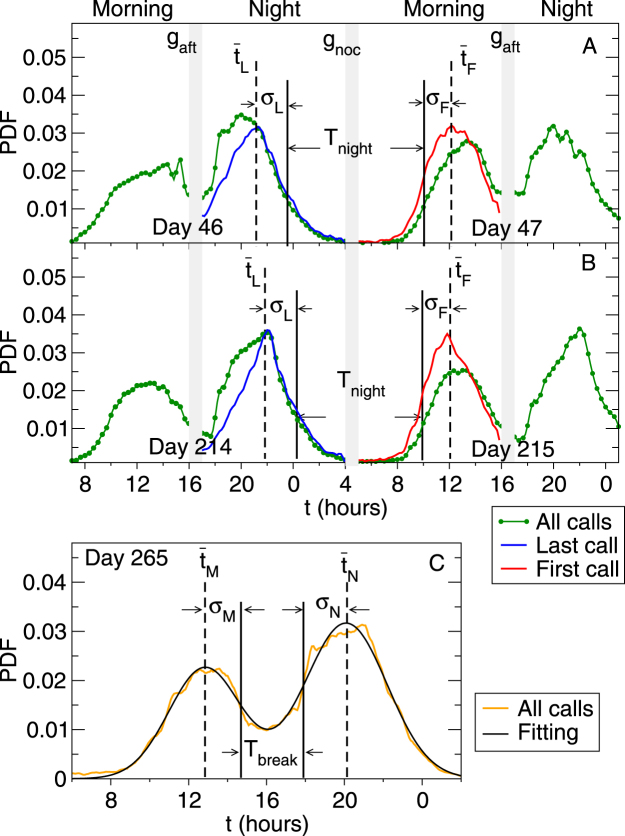
PMC Copyright notice

(Top panel) Probability distribution functions (PDF) of outgoing calls at time t of the day in a city for two sets of consecutive days of 2007: P _all when all the outgoing calls are included (Green), P _L when only the last outgoing calls in the night are included (Blue), and P _F when only the first outgoing calls in the morning are included (Red). From P _L and P _F, their means, ${\bar{t}}_{L}$ and ${\bar{t}}_{F}$ , and their standard deviations σ _L and σ _F, respectively, are calculated and used to define the period of low calling activity (PLCA) as the region bounded by ${\bar{t}}_{L}$ and ${\bar{t}}_{F}$ and determine its width T _night as the time interval between ${\bar{t}}_{L} + σ_{L}$ and ${\bar{t}}_{F} - σ_{F}$ . For the day 46 (middle of February, set A), T _night ≈ 10.5 hours, whilst for the day 214 (early August, set B), T _night ≈ 9.5 hours. (Note that P _all is delimited by the nocturnal calling gap g _noc (between 4:00 a.m. and 5:00 a.m.), P _L lies between the diurnal calling gap g _aft (from 4:00 p.m. to 5:00 p.m.) and g _noc, whilst P _F is bounded by g _noc and g _aft). (Bottom panel) Probability distribution of outgoing calls during the day 265 (Sunday, orange line) in a city (of label 2), fitted by a superposition of two normal (Gaussian) distributions (black line), the first centered round noon and the second one in the evening (8 p.m.). The fitting is done with the mean values t _M and t _N, and the standard deviations σ _M and σ _N, corresponding to the noon and evening-centered activity modes, respectively (see details in the text). The afternoon break period T _break is defined as $(t_{N} - σ_{N}) - (t_{M} + σ_{M})$ .