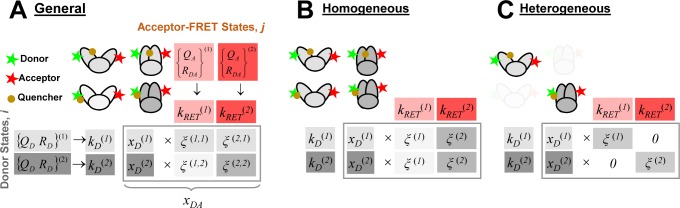
Figure 5.
In a general framework for the analysis of time-resolved FRET experiments, a conditional probability matrix relates the acceptor to the donor states. Schematics illustrating the meaning and relation of the parameters in the eq 23. The donor states, indicated by green shades, are characterized by sets of variables {QD, RD}(i), defining corresponding rate constants kD(i), and their fractions xD(i). The acceptor FRET states are characterized by sets of variables {QA, RDA}(j), defining corresponding FRET rate constants kRET(i), and are indicated by red shades. The gray frame outlines the fraction matrix [xDA(i,j)] of FRET pairs where the donor is in state i and the acceptor in state j. This matrix is presented implicitly by the row product of the donor fraction vector xD and conditional probability matrix [ξ(i,j)] (shades of gray). The gray shades of the protein picture shown in the top left edges illustrate different correlation between donor and acceptor-FRET parameters and indicate corresponding values of the [xDA(i,j)] matrix (the darker shades correspond to the higher fractions). Note that the structure of matrix [xDA(i,j)] and [ξ(i,j)] is not the same. (A) The general case. (B) The homogeneous case. In this case the donor fluorescence decay can be factorized in form of eq 11 and the matrix [ξ(i,j)] has special, uniform-row shape. (C) Case of the full correlation between donor and acceptor states. In this case the number of FRET states is reduced to the number of donor or acceptor states, and the conditional probability matrix turns into an identity matrix.