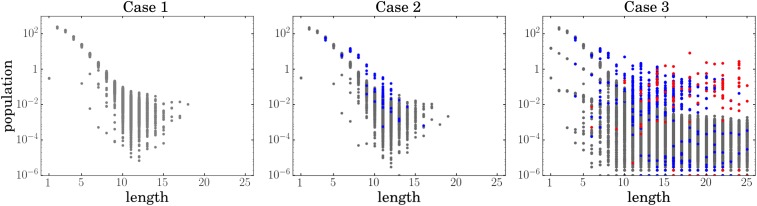
Fig. 5.

The distributions over individual sequences are highly heterogeneous. We show the populations (molecule counts of individual sequences) for the three cases. In case 1, we do not allow folding or catalysis. In case 2, we allow folding but not catalysis, and in case 3, both folding and catalysis are allowed. For all of the cases, gray dots represent populations of the sequences that cannot fold, blue dots represent sequences that fold but cannot catalyze, and red dots represent sequences which act as catalysts and for which at least one elongation reaction has been catalyzed. For cases 1 and 2, populations of the sequences of the given length are distributed exponentially. Thus, we can take mean or median population for the given length as a faithful representation of the behavior of average sequence of that length. Case 3 is drastically different: the populations of the sequences of the given lengths are distributed polynomially. While most of the sequences have very low population for the longer chains, several sequences (mostly autocatalytic ones) have very high ones and constitute most of the biomass. For case 3, neither mean nor median is a good representation of the behavior of the chains; as we can see from the figure, all of the chains basically separate into two groups with different distributions, and this information cannot be shown in the mean or median. Every point is a time average over ${10}^6$ time points in the steady-state interval. Lower limit of ${10}^{-6}$ is because of computational precision.