Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2017 Sep 12;7:11269. doi: 10.1038/s41598-017-11590-6

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2017

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

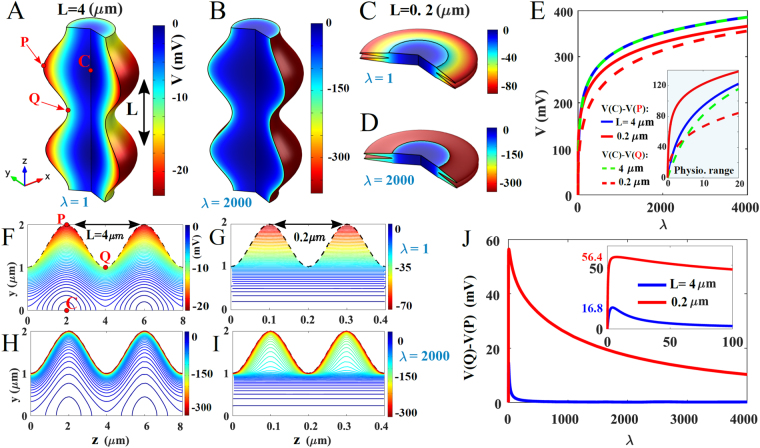
PMC Copyright notice

Numerical evaluation of voltage distribution in a corrugated cylinder (A–D). Voltage distribution computed for λ = 1 (A–C) and λ = 2000 (B–D). The boundary of the cylinder around the symmetry z− axis is defined by the curve γ(z) = 1 + 0.5 sin(2πz/L), where L is a parameter (L = 4 μm (A,B), and L = 0.2 μm (C,D). (E) Voltage differences V(C) − V(Q) (dashed line) and V(P) − V(C) (solid line) versus λ, computed for L = 0.2 μm (red) and L = 4 μm (blue, green), where P (resp. Q) is the maximum (resp. minimum) of the curve γ(z) and C is defined by V(C) = min(V).The inset panel in (E) represents a magnification of the range of λ corresponding to physiological values of the voltage. (F–I) Isopotential lines in the yOz plane, computed for various (λ, L): (F) (1, 4), (G) (1, 0.2), (H) (2000, 4), and (I) (2000, 0.2). (J) Voltage difference V(Q) − V(P) versus λ, computed for L = 4 μm (blue) and L = 0.2 μm (red). The inset in panel J is a magnification of the small λ region.