Figure 4.

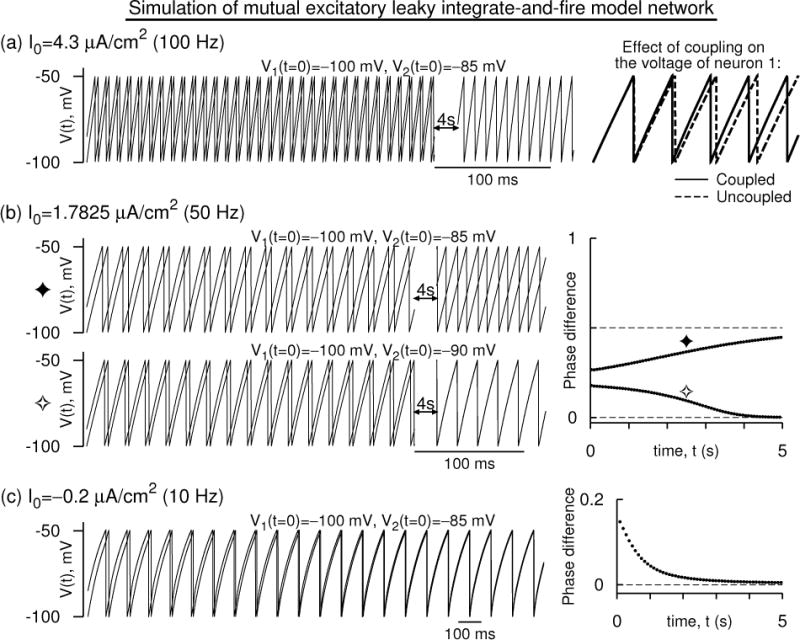
Simulation of a mutually excitatory network of two leaky integrate and fire neurons whose voltages are modeled according to those of the Wang-Buzsáki model. (a) The voltage time courses [V₁(t), V₂(t)] evolving in time and approaching a synchronous oscillatory state at a firing frequency of 100 Hz. Spikes are not part of the model, and hence are not drawn. On the right, the effect of the coupling on V₁(t) is shown - it is excitatory. (b) Time courses as in (a) but at 50 Hz. Two sets of initial conditions lead to two different states: antisynchrony for widely separated initial conditions, and synchrony for closely separated initial conditions. Right: The difference of successive spike times of the neurons normalized to the instantaneous period of one of the neurons (i.e the phase difference) is shown for the two sets of initial conditions. (c) As in (b) but at 10 Hz. Synchrony and anti synchrony are both unstable, but a near synchronous state that is very close to the synchronous state is stable. For all the simulations The parameters are G_L = 0.01 mS/cm², E_L = 0 mV, C_m = 1 μF/cm², V_reset = −100 mV, V_th = −49.5635 mV. E_syn = 10 mV, α = 1/3 ms⁻¹, and $\overline{g}=0.04\text{mS}/{\text{cm}}^2$.