Abstract
We identify a new material phenomenon, where minute mechanical manipulations induce pronounced global structural reconfigurations in faceted multiwalled nanotubes. This behavior has strong implications on the tribological properties of these systems and may be the key to understand the enhanced interwall friction recently measured for boron-nitride nanotubes with respect to their carbon counterparts. Notably, the fast rotation of helical facets in these systems upon coaxial sliding may serve as a nanoscale Archimedean screw for directional transport of physisorbed molecules.
Keywords: Nanotube, friction, faceting
Nanotubes1−5 form a paradigmatic family of quasi-one-dimensional materials playing a central role in the design of many nanoelectromechanical systems.6−19 Traditionally, they are perceived as miniature cylinders of nanoscale circular cross-sections. Nevertheless, if the chirality of neighboring shells within a concentric multiwalled nanotube is correlated, extended circumferential facets may form.20−26 The resulting polygonal cross section induces geometric interwall locking that can considerably enhance their mechanical rigidity.15
Despite their remarkable structural similarity, faceting is more commonly observed in multiwalled boron-nitride nanotubes (MWBNNTs)15,17,25,26 than in their carbon counterparts (MWCNTs).21−24 This can be attributed to three important factors: (i) stronger long-range dispersive attractive interactions exhibited by the former27−29 that provide higher interwall adhesion thus favoring facet formation; (ii) softer ZA modes of h-BN30 that allow for sharper vertices thus promoting the formation of wider planar facet regions; and (iii) higher interwall chiral angle correlation exhibited by MWBNNTs over MWCNTs26,31−43 that induces extended lattice registry patterns between adjacent tube shells and dictates the nature of the facets.20,44 The latter is mainly due to the additional interwall electrostatic interactions between the partially charged ionic centers in the heteronuclear BNNT network. While being relatively weak locally,45,46 when summed over extended commensurate facet regions these Coulomb interactions can foster energetic stabilization.
Similar to macroscopic objects, the strain developing within the hexagonal lattice of nanotubes under small external mechanical manipulations is proportional to the applied stress. Due to their exceptionally high rigidity this usually leads to minor structural deformations. In the present study, however, we discover a new material phenomenon, occurring in faceted double-walled nanotubes (DWNTs), where minute mechanical manipulations induce pronounced global superstructure reconfiguration. For monochiral DWNTs that exhibit axially aligned facets20 even the slightest interwall rotation induces significant circumferential facet revolution, and minor interwall telescoping can lead to complete unfaceting. Similar manipulations applied to bichiral DWNTs result in global screw-like motion of their elongated helical facets reminiscent of an Archimedean screw. Importantly, these superstructure evolutions under coaxial sliding open new collective energy dissipation channels that enhance interwall dynamic friction. This, in turn, suggests that the relative abundance of faceting in MWBNNTs plays a central role not only in their enhanced torsional stiffness15 but also in the significantly higher interwall friction that they exhibit with respect to MWCNTs.47
Facet Superstructure Reconfiguration
To demonstrate the phenomenon of superstructure reconfiguration we consider a set of four representative double-walled BNNTs (DWBNNTs), including the achiral armchair (104,104)@(109,109) and zigzag (180,0)@(188,0) DWBNNTs that present axial facets; the bichiral (70,70)@(77,74) system, whose small interwall chiral angle difference of ΔΘ = 0.657° induces helical facets; and the achiral mixed (179,0)@(108,108) DWBNNT (ΔΘ = 30°) that does not form circumferential facets.20 Here, the notation (n1,m1)@(n2,m2) represents a (n1,m1) inner tube concentrically aligned within an outer (n2,m2) tube, where ni and mi are the corresponding tube indices.48
Focusing first on interwall rotations of the achiral systems, we perform a set of constrained energy minimizations starting from a circular DWBNNT configuration and relaxing the geometry at several fixed interwall angular orientations ranging from 0° to 2°. Figure 1 presents the corresponding relaxed structures of the armchair (104,104)@(109,109) (first row) and the zigzag (180,0)@(188,0) (third row) DWBNNTs. As is evident from the figure, the angular orientation of the facets shows strong dependence on the interwall rotation angle. In the armchair case, which presents an optimal structure of pentagonal cross section, a dramatic 41.8° revolution of the facet superstructure is obtained for every nominal interwall rotation of 2°. Similarly, the octagonal circumferential superstructure of the zigzag case revolves by as much as 45° at a similar interwall rotation of 2°.
Figure 1.
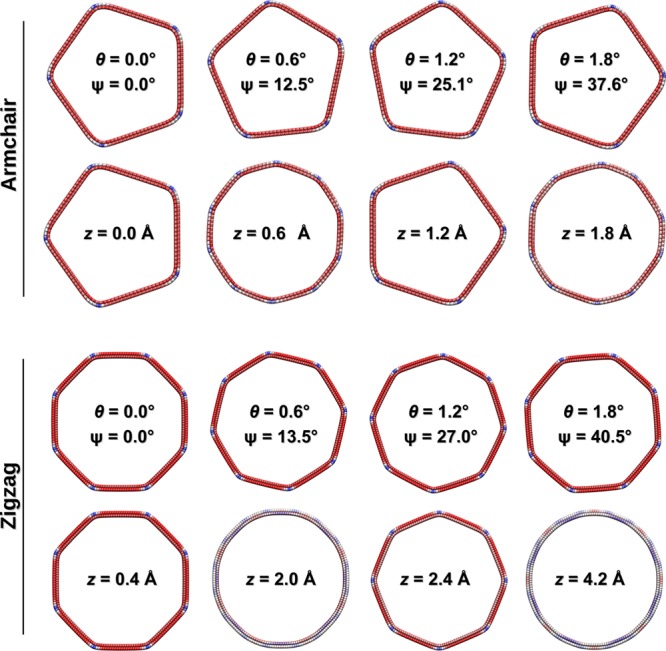
Achiral faceting. Cross-sectional view of the achiral armchair (top rows) and zigzag (bottom rows) DWBNNTs during a full coaxial sliding cycle. Each row shows configurations at increasing relative angular (θ) or axial (z) difference between the outer and inner walls. Continued motion beyond the domain considered herein results in periodic repetitions of the presented structures. Ψ indicates the corresponding facet rotation angle. Intermediate configurations during the adiabatic pull-out process appear in Supporting Information Movie 1. Red, white, and blue colors indicate low, average, and high atomic interlayer energy, respectively.
All the more pronounced structural variations arise in response to interwall telescoping. For the armchair DWBNNTs considered (second row of Figure 1) the number of facets doubles from 5 to 10, and their angular orientation rotates by 18° upon interwall telescoping of 1.25 Å. Notably, for the zigzag DWBNNT (lowest row of Figure 1) almost complete unfaceting is observed upon an axial shift of merely ≃1.7 Å. The entire structural variation progression obtained during an adiabatic pull-out of 4.2 Å is reported in Supporting Information Movie 1.
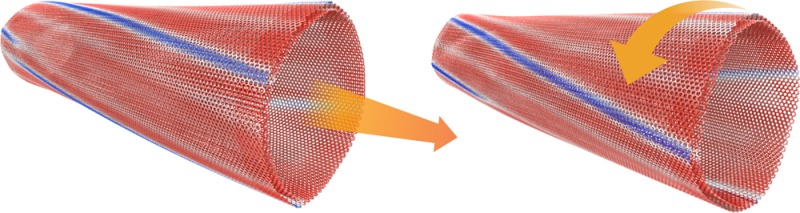
The most remarkable structural response is exhibited by the bichiral (70,70)@(77,74) DWBNNT. The chiral facets appearing in this system couple the translational and rotational degrees of freedom. Hence, interwall telescoping induces global rotation of the entire helical superstructure reminiscent of an Archimedean screw (see Figure 2 and Supporting Information Movie 3). This represents the smallest device exhibiting unidirectional helical motion that may be utilized as a nanoscale arterial thoroughfare for molecular transport.
Figure 2.
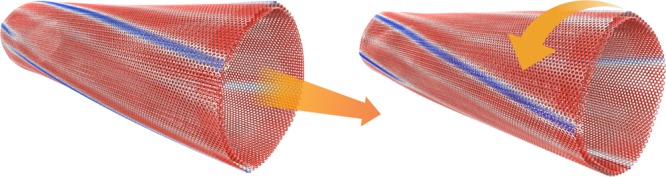
Bichiral DWNT facet rotation. Perspective view of the bichiral (70,70)@(77,74) DWBNNT at two interwall configurations θ/z of 0.2°/2.4 Å (left) and 0.2°/3.2 Å (right). These correspond to configurations close to maximum and minimum potential energy, respectively (see top-right panel of Figure 3). Blue and red atom false coloring represents high and low interlayer energy, respectively. Facet dynamics during a pull-out simulation at an interwall velocity of 0.01 Å/ps is reported in Supporting Information Movie 3.
On the contrary, the achiral mixed zigzag@armchair (179,0)@(108,108) DWBNNT that possesses the maximal interwall chiral angle difference of ΔΘ = 30° presents a featureless circular cross section (not shown) regardless of the interwall position.
Potential Energy Landscapes
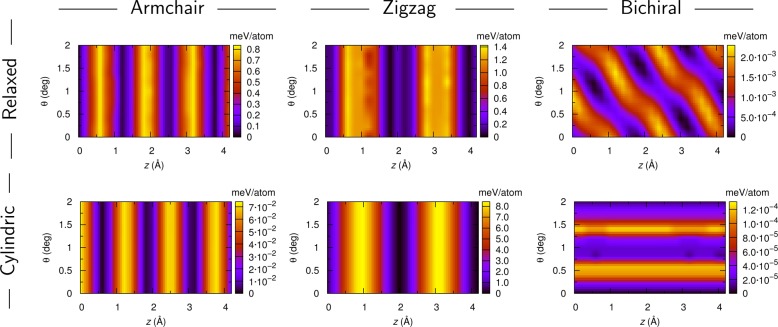
The significant superstructure variations described above are expected to have distinct manifestation in the mechanical and tribological characteristics of faceted nanotube structures. To evaluate these, we compare, in Figure 3, the potential energy surface (PES) for interwall rotation and telescoping of the faceted DWBNNTs (for the carbon counterpart, see Supporting Information Figure S1) considered with those of their circular cross-section counterparts (see Structures and Methods section for technical details regarding the calculation).
Figure 3.
PES maps. Potential energy surface maps of the considered armchair (left column), zigzag (center column), and bichiral (right column) DWBNNTs for the relaxed (top panels) and cylindric (bottom panels) configurations.
Focusing first on the armchair (104,104)@(109,109) DWBNNT (left column in Figure 3), we find, as expected, that the potential energy corrugation for interwall rotations of the circular configuration is very small (2.7 × 10–4 meV/atom). This results from the interwall curvature difference that induces circumferential incommensurability between the hexagonal lattices of the two nanotube shells.49 Interestingly, the faceted configuration maintains a smooth interwall rotation energy landscape (corrugation of 3.0 × 10–5 meV/atom) indicating in addition that pure adiabatic facet reorientation is practically a barrierless process. On the contrary, even for the circular configuration, interwall telescoping is associated with potential energy variations that follow the mutual hexagonal lattice periodicity, pz, along the zigzag axial direction of the two nanotube walls (pz = l√3 ≃ 2.498 Å, where l = 1.442 Å is the equilibrium BN bond length). Notably, for the faceted configuration the amplitude of these variations is an order of magnitude larger (0.84 meV/atom) than that of the circular system (0.074 meV/atom), as is also reflected by the energy landscapes of Figure 3. This is due to the unfaceting and refaceting restructuring sequence occurring during the pull-out process (see Supporting Information Movie 2). At the faceted configuration the average interwall distance reduces from its circular cross-section value of 3.44 Å, a value geometrically determined by the lattice indices of the two walls and by l, to an optimal interfacet separation of 3.27 Å, matching the equilibrium h-BN bilayer interlayer distance of our interatomic potential (see Structures and Methods section). Hence, the overall interwall steric repulsion increases with respect to the unfaceted configuration resulting in higher telescoping PES barriers.
The zigzag (180,0)@(188,0) DWBNNT exhibits similar behavior with smooth interwall rotation (1.4 × 10–4 and 6.1 × 10–5 meV/atom for the circular and faceted configurations, respectively) and a corrugated telescoping PES (middle column in Figure 3). The latter now follows the periodicity, pa, of the armchair axial direction of the two nanotube walls (pa = 3l = 4.326 Å). Unlike the armchair DWBNNT case discussed above, here the circular zigzag DWBNNT configuration presents considerably higher corrugation (8.4 meV/atom) than the faceted one (1.4 meV/atom). This results from the fact that the interwall distance in the frustrated circular system, 3.18 Å, is smaller than the optimal value. Upon facet formation, the interfacet distance now increases to a nearly optimal value of 3.25 Å. This, in turn, results in lower barriers along the unfaceting and refaceting sequence obtained throughout the pull-out process.
An overall lower PES corrugation is presented by the circular bichiral (70,70)@(77,74) DWBNNT (right columns of Figure 3) with relatively smooth telescoping and interwall rotation energy profiles (2.3 × 10–8 and 1.3 × 10–4 meV/atom, respectively). This mainly results from the fact that the interwall distance at this configuration, 3.78 Å, is considerably larger than the equilibrium value. Similar to the case of the armchair system described above, the appearance of facets effectively reduces the interfacet distance toward the equilibrium value resulting in an increase of the PES corrugation. Nevertheless, while the translational and rotational degrees of freedom remain decoupled in the achiral systems that present axial facets, here they are strongly coupled by the helical facets as demonstrated by the tilted (rather than vertical or horizontal) PES ridges.
Interestingly, the achiral mixed (179,0)@(108,108) DWBNNT has an interwall distance of 3.21 Å, comparable to that of the zigzag (180,0)@(188,0) DWBNNT and smaller than the equilibrium value. One might therefore conclude that the two systems should present similar PES corrugation. Nevertheless, the former presents a completely flat translational–rotational PES for both the constrained circular and the fully relaxed configurations (not shown). This may be attributed to the incommensurability of the two hexagonal lattices in both the axial and circumferential directions obtained at the maximal interwall chiral angle misfit of 30°.
Interwall Static Friction
A 2-fold effect of circumferential faceting on the interwall PES of DWBNNTs is thus found: (i) facet restructuring during interwall displacements results in interwall distance variations that may increase or decrease PES corrugation depending on the corresponding distance within the unfaceted system; (ii) helical facets, appearing in bichiral DWBNNTs, couple the translational and rotational degrees of freedom. The immediate physical manifestation of these effects is expected to appear in the static interwall friction exhibited by the DWNT.
The static friction force is defined as the minimal force required to initiate relative motion between the two nanotube walls that are initially interlocked in a (local) free-energy minimum. Despite the general nonuniformity of real telescopic sliding, also depending on the pulling mode, static friction may, in the low temperature limit (T → 0 K), be estimated from the interwall telescoping-rotation PES by evaluating the energy barrier required to lift the interface out of the equilibrium state. To this end, we plot the energy variations during adiabatic axial interwall pull-out and rotation and fit them to a sinusoidal curve of the form E(z) = (Ec/2) sin(2πz/Δz) (see Supporting Information Figure S2). The static friction is then extracted from the maximal derivative of the fitted curve given by Fs = πEc/Δz. A summary of the obtained PES corrugation and the corresponding static friction values appears in Supporting Information Table S1.
As may be expected, for the achiral armchair and zigzag systems, the static friction force required to initiate interwall rotational motion is negligible compared to that necessary to trigger telescopic sliding for both the circular and the faceted configurations. The pull-out static friction force of the armchair DWBNNT at the circular geometry is 0.17 meV/Å per atom, much lower than the corresponding value of the zigzag system (11.8 meV/Å). As discussed above, in the relaxed configuration, the interfacet distance approaches the equilibrium value in both systems resulting in similar friction forces of 1.91 and 2.04 meV/Å per atom for the armchair and zigzag DWBNNTs, respectively.
The bichiral system in its circular geometry presents a negligible static friction force for axial shifts (3.8 × 10–8 meV/Å per atom), while a larger value, yet considerably smaller than the characteristic forces exhibited by the achiral systems, is obtained for interwall rotations (2.2 × 10–4 meV/Å per atom). At the faceted configuration the static friction forces for both telescoping and rotation increase yielding values of about 3.5 × 10–3 and 2.5 × 10–3 meV/Å per atom, respectively. It is clear from the upper right panel of Figure 3 that a combined rotation and telescoping displacement path, which follows the facet helicity, will result in a considerably lower static friction force. For the mixed achiral DWBNNT, considering that, as mentioned above, it exhibits completely flat rotation-telescoping PES maps for both the circular and relaxed (unfaceted) geometries, we could not extract any meaningful static friction force values.
Dynamic Friction
Not only do the superstructure reconfigurations described above impact the static nanotube interwall friction, but they provide a key to understanding the surprisingly high interwall dynamic friction recently measured for MWBNNTs with respect to their carbon counterparts.47 The underlying mechanism relates to the fact that the facet superstructural collective degrees of freedom introduce auxiliary energy dissipation routes that enhance dynamic friction. This is true for both translational and rotational interwall motion even when the latter presents negligible PES corrugation and static friction forces.
To quantify these effects, we performed fully atomistic molecular dynamics interwall sliding simulations (see Structures and Methods section for details) of the DWBNNTs considered. When following the structural variations occurring during the telescopic pull-out of the armchair and zigzag DWBNNTs’ inner shells at a relative velocity of 0.01 Å/ps, we observe a full unfaceting and refaceting superstructure cycle, superposed on asymmetric deformations induced by inertial effects (see Supporting Information Movie 2). For the bichiral DWBNNT, we find that telescopic motion, at the same relative axial velocity, induces circumferential rotation of the helical facets with an angular velocity of about 0.24°/ps (evaluated from the simulated time evolution in Supporting Information Movie 3). This corresponds to a linear superstructure surface velocity of ∼0.2 Å/ps (assuming an average tube diameter of ∼10 nm), which is about 20 times faster than the applied axial velocity.
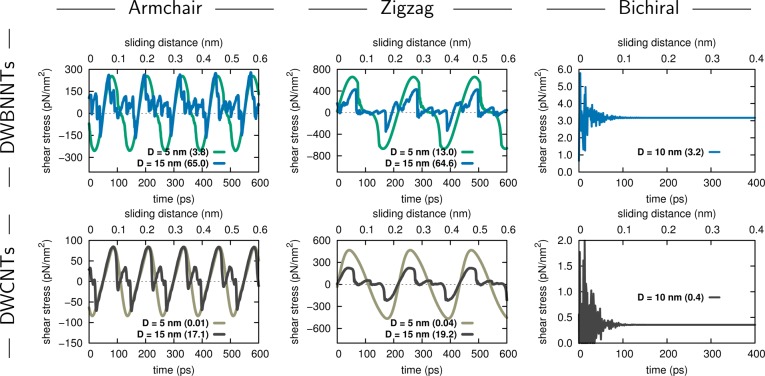
Following Newton’s first law, we define the instantaneous dynamic friction force as the force required to maintain a constant velocity relative interwall sliding motion. To allow for comparison between DWNTs of different diameters we extract the shear stress by normalizing the calculated forces to the nominal surface contact area. In Figure 4 the temporal shear stress traces obtained during constant velocity inner shell pull-out (see Structures and Methods section) are reported. We start by considering the achiral armchair (104,104)@(109,109) and zigzag (180,0)@(188,0) DWBNNTs (blue lines in the upper left and middle panels, respectively). To evaluate the effect of facet reconfiguration on the dynamic friction force, we perform reference calculations on narrow armchair (31,31)@(36,36) and zigzag (55,0)@(63,0) DWBNNTs (green lines in the upper left and middle panels, respectively) that are below the critical diameter for facet formation.15,20
Figure 4.
Dynamic friction. Instantaneous friction force per unit area (shear stress), calculated for interwall telescopic motion of armchair (left panels), zigzag (center panels), and bichiral (right panels) DWBNNTs (upper panels) and DWCNTs (lower panels) of diameter D at a pull-out velocity of 0.01 Å/ps. For the bichiral case, the initial transient dynamics is also shown. The average steady-state friction force values are reported in brackets in units of pN/nm2.
Due to their axial interwall translational symmetry, the achiral DWNTs present periodic dynamic friction force variations with large peak values reflecting increased interfacial commensurability. Interestingly, the overall amplitude variations of the shear stress traces of the faceted DWBNNTs are comparable to those of the narrower circular systems. Nevertheless, while the circular systems present a nearly sinusoidal smooth behavior, the faceted DWBNNTs show a complex pattern of rapid force fluctuations with clear asymmetry between the positive and negative shear stress regions. This is a clear manifestation of the effects of superstructure reconfigurations occurring during the pull-out dynamics in the presence of facets. As a consequence, the dynamic friction force, evaluated as the time averaged shear stress over an integer number of periods, is found to be 5–17 times larger in the faceted achiral DWBNNTs than in the circular systems studied.
We may therefore conclude that faceting, which, as discussed above, is considerably more prevalent in MWBNNTs than in MWCNTs, may be responsible for the enhanced friction measured for the former. To understand how the interwall friction of the less abundant faceted MWCNTs compares to that of their BNNT counterparts, we have repeated our calculations for the corresponding achiral DWCNTs (see lower panels of Figure 4). Similar to the case of DWBNNTs, the circular achiral DWCNTs show a much smoother and more symmetric shear stress trace (see light-gray lines in the lower left and lower middle panels of Figure 4) resulting in considerably smaller dynamic friction forces than the faceted achiral systems (dark-gray lines). Interestingly, even for the latter, the kinetic friction force extracted is smaller by a factor of 3.4–3.8 than that of the corresponding faceted DWBNNTs with the force-field parameters used herein (see Structures and Methods section). Importantly, this is true also for the zigzag (180,0)@(188,0) DWNTs considered, where the PES corrugation of the BN-based system was found to be comparable to that of its carbon counterpart (Figures 3 and S1).
For the bichiral (70,70)@(77,74) DWBNNT considered, no periodic kinetic friction force variations are observed (see upper right panel of Figure 4). Furthermore, following some initial transient dynamics, smooth steady-state sliding motion with nearly constant drag is obtained. This can be attributed to the reduced interwall commensurability and PES corrugation in this system (see right panels of Figure 3). Consequently, the average dynamic friction force recorded in this case (∼3.2 pN/nm2) is 20-fold times smaller than that of the faceted achiral systems. Nevertheless, it remains nearly an order of magnitude larger than the value measured for the corresponding bichiral DWCNT (0.4 pN/nm2, see lower right panel of Figure 4) and a factor of 80–320 larger than the kinetic friction measured for the achiral circular DWCNTs considered.
Finally, we study the velocity dependence of the interlayer sliding friction of DWBNNTs and DWCNTs in the range of 0.2–1.0 m/s (see Supporting Information Figure S5). Our results show a nearly linear increase of the friction force with the sliding velocity at the velocity range considered. For the axially commensurate armchair DWNTs, the friction extrapolates to a finite value at zero velocity. This can be attributed to the finite static friction exhibited by these systems. For the incommensurate bichiral DWNTs the friction extrapolates to zero at vanishing interwall sliding velocity. This is in line with the experimental observation of viscous interwall telescopic motion in multiwalled NTs, where sliding is expected to occur at the weakest incommensurate interface. The calculated interwall friction forces in both DWCNTs considered are found to be weakly dependent on the sliding velocity and are consistently lower than those obtained for the corresponding DWBNNTs. This further supports the experimental observations of increased interwall friction in MWBNNTs over MWCNTs.47
Conclusions
The resulting screw-like motion of the faceted helical pattern establishes the smallest realization of an Archimedean screw with the potential to achieve directional transport of weakly adsorbed molecules along the surface of the tube.
We note that the superstructure variations discussed above may be viewed as the nanotube analogues of the soliton-like motion of moiré patterns occurring in sliding incommensurate planar interfaces.50 Nevertheless, due to geometric frustration in the tubular configuration, the extended circumferential registry patterns result in considerably larger structural deformations. The latter exhibit much richer dynamic behavior with marked influence on the mechanical, tribological, and electronic properties of the system.
The motion of such collective degrees of freedom opens new dissipative channels that enhance dynamic friction beyond the excitation of localized phonon modes. Since faceting is more commonly observed in MWBNNTs than in their carbon counterparts, this rationalizes recent experimental findings showing that the former exhibit an order of magnitude larger dynamic friction.47 Furthermore, even when compared to the less abundant case of faceted DWCNTs, the BN systems exhibit 3–8 times larger dynamic friction forces. Hence, when designing smooth nanoscale bearings, one should resort to unfaceted MWCNTS,49 whereas if torsional and axial rigidities are desired, faceted MWBNNTs should be the material of choice.15,47
Finally, several other, more speculative but highly intriguing, consequences of the striking facet evolutions discussed herein can be envisioned. First, we have shown that facet dynamics strongly depend on the relative chirality of adjacent nanotube walls. Therefore, the interwall pulling force trace should encode information about the identity of the various tube shells. This, in turn, opens new opportunities for novel material characterization techniques that may provide access to the specific sequence of chiralities of successive nanotube walls. Furthermore, electronic effects, not discussed herein, may also exhibit unexpected behavior. Specifically, surface states that typically localize at sharp edges, such as the circumferential vertices of the polygonal cross-section, may also be pumped along the surface of nanotubes in an Archimedean manner.
Structures and Methods
DWNTs can have inner and outer walls that are zigzag (ZZ), amrchair (AC), or chiral (Ch). In the present study four types of carbon and boron nitride (BN) DWNTs have been considered including the achiral AC@AC (104,104)@(109,109) and ZZ@ZZ (180,0)@(188,0) systems; the mixed achiral ZZ@AC (179,0)@(108,108); and the bichiral AC@Ch (70,70)@(77,74). Here, the notation (n1,m1)@(n2,m2) represents a (n1,m1) inner tube concentrically aligned within an outer (n2,m2) tube, where ni and mi are the corresponding tube indices. Monochiral DWNTs that have chiral walls with matching chiral angles present axial facets like the achiral systems20 and are therefore not considered herein. A summary of the relevant geometric parameters of the unrelaxed DWNTs appears in Table S2.
The structural and frictional properties of all DWNTs considered have been described using dedicated intra- and interlayer classical force-fields as detailed below. For DWCNTs, the intralayer interactions have been described using the Tersoff51 potential adopting the parametrization of Lindsay and Broido.52 The interlayer interactions of these systems have been described by the registry-dependent Kolmogorov–Crespi potential in its RDP1 form.44 For the intralayer interactions of DWBNNTs, we have used the Tersoff force-field as parametrized by Sevik et al. for BN-based systems,53 along with our recently developed h-BN interlayer potential with fixed partial charges.29,54 We note that suppressing the Coulombic interactions between the partially charged atomic centers in the DWBNNTs studied (qB = +0.47 e, qN = −0.47 e) results in a reduction of merely ∼3.5% in their calculated PES corrugation (see Supporting Information Figure S3). Corrugation and adhesion energy profiles for rigid planar bilayer of h-BN and graphene, as obtained by the above set of interlayer potentials, are reported in Supporting Information Figure S4.
Periodic boundary conditions (PBC) along the tube axis have been applied to all DWNTs considered, resulting in a very small (<0.1%) stress in the case of the bichiral and mixed systems due to the different lattice constants of the inner and outer tubes. In all cases, an initial step of relaxation of the cell vectors has been performed in order to minimize any PBC-related stress effects.
In the pull-out/rotation potential energy surface calculations (Figure 3) each point has been obtained by placing the two unrelaxed cylindrical nanotube walls at the corresponding relative axial and angular position followed by geometry optimization using FIRE quenched dynamics,55 while nullifying the center of mass (c.o.m.) axial and angular velocity of each nanotube wall. All the constrained relaxations were stopped after 5000 FIRE iterations, providing energy evaluations that are converged to within 0.1% of the highest energy obtained across the PES maps. The reported energy per atom has been obtained by dividing the converged energy by the total number of atoms in the DWNT. We note that this procedure corresponds to an adiabatic relative motion of the tubes that can, in principle, be realized in experiment by adhering the outer tube wall(s) to a fixed stage and applying a slowly varying external force on the inner shells via the manipulation of an external tip.47,56−58 Although in typical experimental setups the external force is applied at one edge of the inner shell, their extreme stiffness permits the instantaneous propagation of the stress along the entire tube length. Hence, the calculated PESs should reliably describe the corresponding interwall energy variations measured in the experiment.
Dynamic friction calculations have been performed by numerically propagating the Langevin equation of motion using the standard molecular dynamics velocity–Verlet algorithm. The simulations have been performed in the underdamped regime by applying viscous damping to all degrees of freedom apart from the c.o.m. motion of both tubes. The dynamic friction force is evaluated from the interwall shear force required to keep the two nanotube walls at constant relative velocity motion vext. To this end, we have fixed the c.o.m. of the internal tube and applied a uniform force Fext to each of the N atoms of the external tube so that
| 1 |
| 2 |
where vi0 and vi are the i-th atom velocities at times t0 and t1, respectively, Δt = t1 – t0 is the numerical propagation time step, vcm0 is the c.o.m. velocity of the external tube at t = t0, mi the atomic mass, Fi is the total force on atom i due to the chosen set of interatomic potentials, and γ = 0.1 ps–1 is the viscous damping coefficient used in the simulation to avoid system overheating. Since the viscous damping is not applied to the c.o.m. motion of the tubes, the computed friction results weakly dependent on the adopted γ value, the latter mainly determining the steady-state temperature of the sliding system. In our typical simulations, which were run in the underdamped regime, we measured steady-state temperatures below 1 K, suggesting a negligible role of temperature on the measured friction.
| 3 |
where
| 4 |
| 5 |
| 6 |
Since Fext is applied to all the atoms of the external tube, the instantaneous friction force of the entire surface, Ffric, is simply expressed by
| 7 |
Finally, the obtained dynamic friction force Ffric is normalized to the interwall contact area evaluated from the average diameter of the unrelaxed-cylindrical configuration (see Table S2), leading to the system-specific shear stress value. This allows for a direct comparison among forces calculated for DWNTs of different type and dimensions. The resulting shear stress has been averaged over a time window of at least 1 ns during the steady-state motion, after the initial transient dynamics has decayed, covering an integer number of oscillations in the case of periodic force traces.
We note that by using this procedure a direct quantitative comparison with experimental data is hard to achieve, due to the large sliding velocities, to which MD simulations are limited, compared to those accessible in realistic experimental conditions. Despite this, our dynamic simulations allow for a comparative study of the tribological properties of faceted and unfaceted DWNTs of different chemical composition.
Acknowledgments
Work in Trieste was carried out under ERC Grant 320796 MODPHYSFRICT. EU COST Action MP1303 is also gratefully acknowledged. O.H. acknowledges the Lise-Meitner Minerva Center for Computational Quantum Chemistry and the Center for Nanoscience and Nanotechnology at Tel-Aviv University for their generous financial support.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.7b01718.
PES of armchair, zigzag, and bichiral DWCNTs (relaxed and cylindric); example of sinusoidal fitting of a PES to estimate static friction; comparison of the PES of armchair DWBNNT with and without partial charges contribution; corrugation and adhesion energy profiles for a bilayer of graphene and of h-BN; effect of sliding velocity on the average friction of armchair and bichiral DWCNTs and DWBNNTs; table reporting evaluated static friction and maximum corrugation energy for the reference DWNTs set; table reporting chiral angle difference, average diameter, and average interlayer spacing for the reference DWNTs set (PDF)
Movie of the cross sectional view of armchair and zigzag DWNTs relaxed at different relative axial positions z (AVI)
Movie showing a comparison of the cross sectional view of the armchair DWBNNT in telescopic motion at zero (adiabatic motion) and at large pulling velocity (AVI)
Movie of the bichiral DWBNNT at large relative pulling velocity (AVI)
Movie of the bichiral DWCNT at large relative pulling velocity (AVI)
Author Contributions
R.G. and I.L. developed the simulation code and performed the calculations. R.G. conceived the method to evaluate dynamic friction, and produced the figures and the movies. All the authors actively participated in the data analysis and in the writing of the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Iijima S. Nature 1991, 354, 56–58. 10.1038/354056a0. [DOI] [Google Scholar]
- Rubio A.; Corkill J. L.; Cohen M. L. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 5081R. 10.1103/PhysRevB.49.5081. [DOI] [PubMed] [Google Scholar]
- Chopra N. G.; Luyken R. J.; Cherrey K.; Crespi V. H.; Cohen M. L.; Louie S. G.; Zettl A. Science 1995, 269, 966. 10.1126/science.269.5226.966. [DOI] [PubMed] [Google Scholar]
- Cohen M. L.; Zettl A. Phys. Today 2010, 63, 34. 10.1063/1.3518210. [DOI] [Google Scholar]
- Tenne R.; Margulis L.; Genut M.; Hodes G. Nature 1992, 360, 444–446. 10.1038/360444a0. [DOI] [Google Scholar]
- De Volder M. F. L.; Tawfick S. H.; Baughman R. H.; Hart A. J. Science 2013, 339, 535–539. 10.1126/science.1222453. [DOI] [PubMed] [Google Scholar]
- Arash B.; Wang Q.; Varadan V. K. Sci. Rep. 2015, 4, 6479. 10.1038/srep06479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen-Karni T.; Segev L.; Srur-Lavi O.; Cohen E.; Joselevich S. R. Nat. Nanotechnol. 2006, 1, 36. 10.1038/nnano.2006.57. [DOI] [PubMed] [Google Scholar]
- Stampfer C.; Jungen A.; Linderman R.; Obergfell D.; Roth S.; Hierold C. Nano Lett. 2006, 6, 1449–1453. 10.1021/nl0606527. [DOI] [PubMed] [Google Scholar]
- Jensen K.; Girit Ç; Mickelson W.; Zettl A. Phys. Rev. Lett. 2006, 96, 215503. 10.1103/PhysRevLett.96.215503. [DOI] [PubMed] [Google Scholar]
- Lucas M.; Zhang X. H.; Palaci I.; Klinke C.; Riedo E.; Tosatti E. Nat. Mater. 2009, 8, 876. 10.1038/nmat2529. [DOI] [PubMed] [Google Scholar]
- Chiu H. C.; Dogan S.; Volkmann M.; Klinke C.; Riedo E. Nanotechnology 2012, 23, 455706. 10.1088/0957-4484/23/45/455706. [DOI] [PubMed] [Google Scholar]
- Zheng Q.; Jiang Q. Phys. Rev. Lett. 2002, 88, 045503. 10.1103/PhysRevLett.88.045503. [DOI] [PubMed] [Google Scholar]
- Nagapriya K. S.; Goldbart O.; Kaplan-Ashiri I.; Seifert G.; Tenne R.; Joselevich E. Phys. Rev. Lett. 2008, 101, 195501. 10.1103/PhysRevLett.101.195501. [DOI] [PubMed] [Google Scholar]
- Garel J.; Leven I.; Zhi C.; Nagapriya K. S.; Popovitz-Biro R.; Golberg D.; Bando Y.; Hod O.; Joselevich E. Nano Lett. 2012, 12, 6347–6352. 10.1021/nl303601d. [DOI] [PubMed] [Google Scholar]
- Levi R.; Bitton O.; Leitus G.; Tenne R.; Joselevich E. Nano Lett. 2013, 13, 3736–3741. 10.1021/nl401675k. [DOI] [PubMed] [Google Scholar]
- Garel J.; Zhao C.; Popovitz-Biro R.; Golberg D.; Wang W.; Joselevich E. Nano Lett. 2014, 14, 6132–6137. 10.1021/nl502161h. [DOI] [PubMed] [Google Scholar]
- Levi R.; Garel J.; Teich D.; Seifert G.; Tenne R.; Joselevich E. ACS Nano 2015, 9, 12224–12232. 10.1021/acsnano.5b05468. [DOI] [PubMed] [Google Scholar]
- Divon Y.; Levi R.; Garel J.; Golberg D.; Tenne R.; Ya'akobovitz A.; Joselevich E. Nano Lett. 2017, 17, 28–35. 10.1021/acs.nanolett.6b03012. [DOI] [PubMed] [Google Scholar]
- Leven I.; Guerra R.; Vanossi A.; Tosatti E.; Hod O. Nat. Nanotechnol. 2016, 11, 1082–1086. 10.1038/nnano.2016.151. [DOI] [PubMed] [Google Scholar]
- Liu M.; Cowley J. M. Carbon 1994, 32, 393–403. 10.1016/0008-6223(94)90159-7. [DOI] [Google Scholar]
- Gogotsi Y.; Libera J. A.; Kalashnikov N.; Yoshimura M. Science 2000, 290, 317–320. 10.1126/science.290.5490.317. [DOI] [PubMed] [Google Scholar]
- Zhang G.; Jiang X.; Wang E. Science 2003, 300, 472–474. 10.1126/science.1082264. [DOI] [PubMed] [Google Scholar]
- Zhang G. Y.; Bai X. D.; Wang E. G.; Guo Y.; Guo W. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 113411. 10.1103/PhysRevB.71.113411. [DOI] [Google Scholar]
- Golberg D.; Mitome M.; Bando Y.; Tang C. C.; Zhi C. Y. Appl. Phys. A: Mater. Sci. Process. 2007, 88, 347–352. 10.1007/s00339-007-3950-8. [DOI] [Google Scholar]
- Celik-Aktas A.; Zuo J. M.; Stubbins J. F.; Tang C. C.; Bando Y. Acta Crystallogr., Sect. A: Found. Crystallogr. 2005, 61, 533–541. 10.1107/S0108767305026723. [DOI] [PubMed] [Google Scholar]
- Hsing C.-R.; Cheng C.; Chou J.-P.; Chang C.-M.; Wei C.-M. New J. Phys. 2014, 16, 113015. 10.1088/1367-2630/16/11/113015. [DOI] [Google Scholar]
- Liu Z.; Liu J. Z.; Cheng Y.; Li Z.; Wang L.; Zheng Q. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 205418. 10.1103/PhysRevB.85.205418. [DOI] [Google Scholar]
- Leven I.; Azuri I.; Kronik L.; Hod O. J. Chem. Phys. 2014, 140, 104106. 10.1063/1.4867272. [DOI] [PubMed] [Google Scholar]
- Wirtz L.; Rubio A.; de la Concha R. A.; Loiseau A. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 68, 045425. 10.1103/PhysRevB.68.045425. [DOI] [Google Scholar]
- Celik-Aktas A.; Zuo J. M.; Stubbins J. F.; Tang C.; Bando Y. Appl. Phys. Lett. 2005, 86, 133110. 10.1063/1.1885177. [DOI] [Google Scholar]
- Golberg D.; et al. J. Appl. Phys. 1999, 86, 2364–2366. 10.1063/1.371058. [DOI] [Google Scholar]
- Golberg D.; Bando Y.; Kurashima K.; Sato T. Solid State Commun. 2000, 116, 1–6. 10.1016/S0038-1098(00)00281-7. [DOI] [Google Scholar]
- Hashimoto A.; et al. Phys. Rev. Lett. 2005, 94, 045504. 10.1103/PhysRevLett.94.045504. [DOI] [PubMed] [Google Scholar]
- Schouteden K.; Volodin A.; Li Z.; Van Haesendonck C. Carbon 2013, 61, 379–385. 10.1016/j.carbon.2013.05.020. [DOI] [Google Scholar]
- Xu Z.; Bai X.; Wang Z. L.; Wang E. J. Am. Chem. Soc. 2006, 128, 1052–1053. 10.1021/ja057303j. [DOI] [PubMed] [Google Scholar]
- Zuo J. M.; Vartanyants I.; Gao M.; Zhang R.; Nagahara L. A. Science 2003, 300, 1419–1421. 10.1126/science.1083887. [DOI] [PubMed] [Google Scholar]
- Li F.; et al. J. Mater. Res. 2003, 18, 1251–1258. 10.1557/JMR.2003.0172. [DOI] [Google Scholar]
- Koziol K.; Shaffer M.; Windle A. Adv. Mater. 2005, 17, 760–763. 10.1002/adma.200401791. [DOI] [Google Scholar]
- Ducati C.; et al. Small 2006, 2, 774–784. 10.1002/smll.200500513. [DOI] [PubMed] [Google Scholar]
- Hirahara K.; et al. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 195420. 10.1103/PhysRevB.73.195420. [DOI] [Google Scholar]
- Gao M.; Zuo J. M.; Zhang R.; Nagahara L. A. J. Mater. Sci. 2006, 41, 4382–4388. 10.1007/s10853-006-0146-0. [DOI] [Google Scholar]
- Guan L.; Suenaga K.; Iijima S. Nano Lett. 2008, 8, 459–462. 10.1021/nl072396j. [DOI] [PubMed] [Google Scholar]
- Kolmogorov A. N.; Crespi V. H. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 235415. 10.1103/PhysRevB.71.235415. [DOI] [Google Scholar]
- Hod O. J. Chem. Theory Comput. 2012, 8, 1360–1369. 10.1021/ct200880m. [DOI] [PubMed] [Google Scholar]
- Lennard-Jones J. E.; Dent B. M. Trans. Faraday Soc. 1928, 24, 92–108. 10.1039/tf9282400092. [DOI] [Google Scholar]
- Niguès A.; Siria A.; Vincent P.; Poncharal P.; Bocquet L. Nat. Mater. 2014, 13, 688. 10.1038/nmat3985. [DOI] [PubMed] [Google Scholar]
- Saito R.; Dresselhaus G.; Dresselhaus M. S.. Physical properties of carbon nanotubes, 1st ed; World Scientific, 1998. [Google Scholar]
- Kolmogorov A. N.; Crespi V. H. Phys. Rev. Lett. 2000, 85, 4727–4730. 10.1103/PhysRevLett.85.4727. [DOI] [PubMed] [Google Scholar]
- Amidror I.The Theory of the Moiré Phenomenon; Springer, 2009. [Google Scholar]
- Tersoff J. Phys. Rev. B: Condens. Matter Mater. Phys. 1989, 39, 5566. 10.1103/PhysRevB.39.5566. [DOI] [PubMed] [Google Scholar]
- Lindsay L.; Broido D. A. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 205441. 10.1103/PhysRevB.81.205441. [DOI] [Google Scholar]
- Sevik C.; Kinaci A.; Haskins J. B.; Çağin T. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84, 085409. 10.1103/PhysRevB.84.085409. [DOI] [Google Scholar]
- Maaravi T.; Leven I.; Azuri I.; Kronik L.; Hod O.. Interlayer Potential for Homogeneous Graphene and Hexagonal Boron Nitride Systems: Reparameterization for Many-Body Dispersion Effects. Submitted.
- Bitzek E.; Koskinen P.; Gahler F.; Moseler M.; Gumbsch P. Phys. Rev. Lett. 2006, 97, 170201. 10.1103/PhysRevLett.97.170201. [DOI] [PubMed] [Google Scholar]
- Yu M.-F.; Yakobson B. I.; Ruoff R. S. J. Phys. Chem. B 2000, 104, 8764–8767. 10.1021/jp002828d. [DOI] [Google Scholar]
- Yu M.-F.; Lourie O.; Dyer M. J.; Moloni K.; Kelly T. F.; Ruoff R. S. Science 2000, 287, 637–640. 10.1126/science.287.5453.637. [DOI] [PubMed] [Google Scholar]
- Akita S.; Nakayama J. Jpn. J. Appl. Phys. 2003, 42, 3933. 10.1143/JJAP.42.3933. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.