Epitaxial graphene homogeneity and quantum Hall effect in millimeter-scale devices

Abstract

Quantized magnetotransport is observed in 5.6 × 5.6 mm² epitaxial graphene devices, grown using highly constrained sublimation on the Si-face of SiC(0001) at high temperature (1900 °C). The precise quantized Hall resistance of $R_{\mathit{\text{xy}}}=\frac{h}{2e^2}$ is maintained up to record level of critical current I_xx = 0.72 mA at T = 3.1 K and 9 T in a device where Raman microscopy reveals low and homogeneous strain. Adsorption-induced molecular doping in a second device reduced the carrier concentration close to the Dirac point (n ≈ 10¹⁰ cm⁻²), where mobility of 18760 cm²/V is measured over an area of 10 mm². Atomic force, confocal optical, and Raman microscopies are used to characterize the large-scale devices, and reveal improved SiC terrace topography and the structure of the graphene layer. Our results show that the structural uniformity of epitaxial graphene produced by face-to-graphite processing contributes to millimeter-scale transport homogeneity, and will prove useful for scientific and commercial applications.

1. Introduction

Wafer-scale monolayer graphene [1,2] can be produced by thermal decomposition of certain polytypes of silicon carbide [3] (SiC) or by chemical vapor deposition (CVD) on metal catalyst substrates [2]. While CVD graphene forms randomly oriented domains to match the crystal orientation of the metal catalyst, epitaxial graphene (EG) forms a single domain on monocrystalline wafers of hexagonal SiC(0001) [4] and the insulating SiC substrate is immediately suitable for fabrication of electronic [5], plasmonic [6] and photonic [7] devices. Quantum Hall effect (QHE) standards produced from EG [8,9] can be operated economically at lower magnetic fields and higher temperatures than GaAs-AlGaAs heterostructures [10]; thus EG devices are likely to become the premier source of resistance traceability in practical metrology and their optimization is of great interest to the electrical metrology community.

Efforts to produce nearly defect-free monolayer EG on SiC generally involve control of the high-temperature vapor phase. For example, annealing in atmospheric-pressure Ar gas [11] or in a small confining enclosure [12] helps to raise the partial pressures of sublimated Si, Si₂C and SiC₂ closer to equilibrium at high temperature, and the number of defects in graphene is then reduced and the morphology of vicinal SiC(0001) surfaces is generally improved. However, dissociated carbon atoms may diffuse anisotropically [13], leading to the formation of multiple graphene layers near the edges of the terraces [14]. Furthermore, SiC restructuring [3] and energetically-favorable step-bunching also may produce undesirable terrace facet edges [14,15] that face off-axis by ≈ 30° on vicinal SiC(0001). Atomic-layer-resolved characterization has shown significant delamination of the carbon buffer layer [15,16] on facet edges that separate adjacent terraces. Here, we report precision measurements of the QHE in millimeter-scale EG devices at high current and correlate the quantized magnetotransport to microscopy data, including structural reorganization of the SiC surface, EG layer number and distribution, and strain as measured by Raman microscopy.

2. Sample preparation

2.1. High temperature EG growth with vapor constraint

To minimize the possible complications due to the substrate, we produce EG using a constraint on vapor diffusion provided by close proximity to polished pyrolytic graphite substrates (SPI Glas 22). The samples were diced from two 76 mm SiC(0001) semi-insulating wafers (Cree, Inc.³) of nominal miscut 0.00°, with sample miscut measured to be ≤ 0.10° from atomic force microscopy (AFM) images. Samples were rinsed in HF and deionized water before processing, and arranged facing to graphite (FTG) with separation distance limited only by sample and substrate flatness (Fig. 1a). Processing was done in a graphite-lined resistive-element furnace (Materials Research Furnaces Inc.) with heating and cooling rates near 1.5 °C/s. The initial heating occurs in forming gas (96% Ar, 4% H₂) at 100 kPa with at least 30 min cleaning of the substrates at 1050 °C, which may serve to hydrogenate the SiC surface [17,18]. The chamber was then flushed with Ar gas, and filled with 100 kPa Ar derived from 99.999% liquid Ar before annealing at 1900 °C. The annealing process utilized a commercial process controller and a type-C thermocouple located a few cm above the sample.

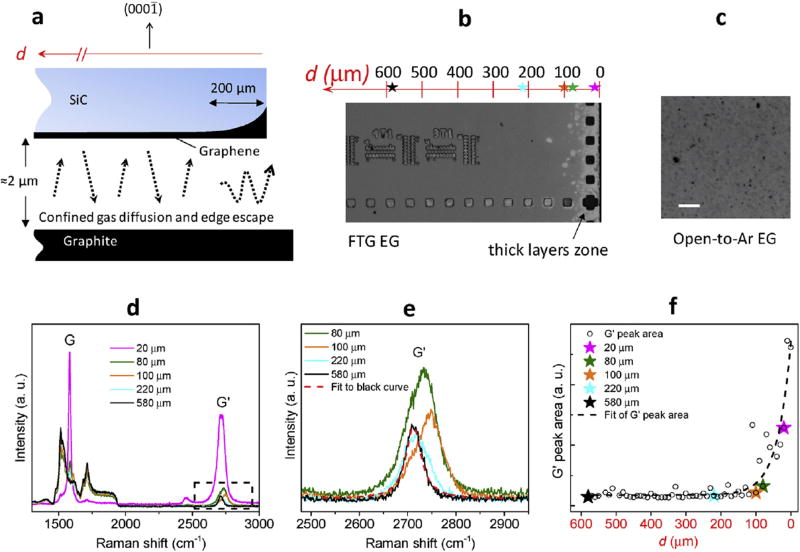
Fig. 1.

(a) Diagram showing a cross-section of the SiC sample and polished graphite during FTG processing. (b) Optical image showing the edge region of a 7.6 mm square sample processed at 1950 °C for 1800 s with FTG configuration. The squares and pattern are fiducials etched into the SiC substrate. (c) Optical image of a sample processed with Si-face open to Ar at 1900 °C for 210 s, showing the center region with non-uniform graphene. The white scale bar is 10 µm. (d) Representative Raman spectra vs. distance from the edge of FTG samples, showing G and G′ Raman peaks of EG at positions d = 20 µm (magenta), 80 µm (green), 100 µm (orange), 220 µm (cyan), and 580 µm (black). (e) Zoom-in of Raman G′ peak spectra from (b), as indicated by the dashed black box. The G′ peak at d = 20 µm is omitted for clarity. The G′ peak at d = 580 µm can be fit well with a single Lorentzian curve as shown. (f) Integrated G′ peak area vs. distance from the sample edge. The locations for the data shown in (d)–(f) are marked by colored stars along the axis above the optical image in (b). The data shown in (d)–(f) are marked with the same color scheme.

Figs. 1b and c show the optical images of two samples processed with and without the FTG configuration, respectively. The sample processed with Si-face open to Ar (Fig. 1c) shows inhomogeneous EG coverage over the entire substrate. The FTG sample (Fig. 1b) has uniform EG coverage (grey area) toward its center, while lower vapor pressure near its borders has allowed the formation of thick, graphitic layers (white area). Raman spectra confirm these results and are shown in Figs. 1d–f from five locations along a linear scan of a FTG sample. Both the G band (≈ 1600 cm⁻¹) and the G′ band (≈ 2700 cm⁻¹) from EG evolve with the distance d from the edge and indicate the variation in layer number. Fig. 1e magnifies the region of the G′ band, excluding the peak at d = 20 µm, and Fig. 1f shows the exponential decrease of the integrated G′ peak area toward the center of the substrate. At interior distances d > ≈ 200 µm, most G′ peaks take on the shape of a single Lorentzian with a full width at half maximum (FWHM) of ≈40 cm⁻¹, which is the fingerprint for identifying monolayer EG.

2.2. Device fabrication and molecular doping

In this paper, we will focus on two FTG-grown samples of size 7.6 × 7.6 mm². We patterned a semi-octagonal active channel utilizing the center region of the FTG samples, which has an area of 27 mm² (see the inset of Fig. 2a). The edge of the active graphene channel is 1 mm from the edge of the substrate so that the periphery region of thick layers is avoided. In fabricating the magnetotransport devices, the active EG surfaces were kept uniformly resist-free by depositing Pd/Au as a thin layer prior to standard photolithography processing, and afterwards removing the Pd/Au layer from the EG region by immersing the devices in dilute aqua regia (by volume, HNO₃:HCl:H₂O = 1:3:4) for 45 s. This fabrication process [19] initiates the attachment of molecular dopants, and can result in carrier concentrations below n ≈ 10¹⁰ cm⁻² in ungated EG samples, compared to as-grown monolayer EG with substrate-induced doping as high as n ≈ 10¹³ cm⁻². The carrier concentration can be tuned by adding or removing molecular dopant using chemical- or heat-treatment (Fig. S7).

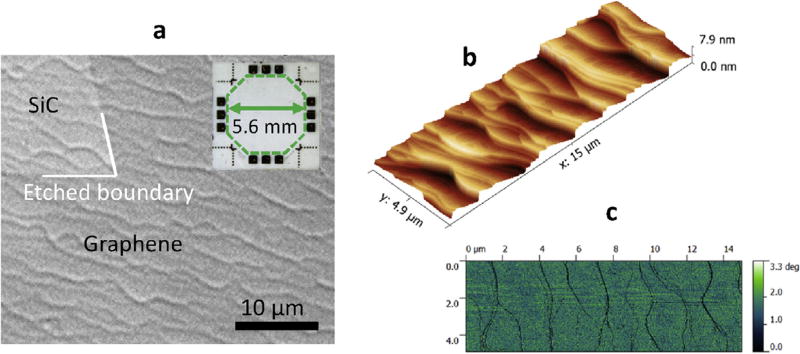
Fig. 2.

(a) Optical image of a region of sample A, with enhanced contrast to show where EG has been removed (upper left of image), labeled SiC. Inset shows a large-scale device with twelve symmetric gold contacts. (b) AFM topography image of a FTG sample with step height displayed as contours in the vertical direction. (c) AFM phase image corresponding to the height image in (b).

3. Characterization

Our present work on devices composed of FTG-grown material shows that the graphene lattice strain and specifically homogeneous low strain is predictive of EG device transport characteristics at millimeter-scale. Exceptional magnetotransport at millimeter-scale was measured in two samples produced using FTG confinement at 1900 °C for 210 s (sample A) and 235 s (sample B). A magnetotransport device of 5.6 mm in height and width was fabricated at the center of each sample, as shown in the inset of Fig. 2a. The surfaces of both samples were characterized by contrast-enhanced optical imaging [20] (Fig. 2a and Supplement Fig. S1), AFM (Figs. 2b and c), and confocal optical microscopy (Figs. 3a and b).

Fig. 3.

Confocal microscopy images of sample A and sample B. (a) Area of sample A, imaged by contrast-enhanced confocal microscopy with reflected 405 nm light. Monolayer graphene appears as a uniform background with terraces barely visible. The square region at upper right is a 500 nm deep etched fiducial mark, showing small fingers of multilayer graphene along its right side, and a bilayer patch just below its lower left corner (indicated by the white arrows). (b) Area of sample B near the left-center contact, imaged by contrast-enhanced confocal microscope with reflected 460 nm light. Monolayer appears as a uniform background, with buffer layer or no graphene showing as darker patches (indicated by the red arrow) and bilayer or multilayer (indicated by the white arrow) appearing as lighter patches or ribbons.

3.1. Optical and atomic force microscopy

The FTG [21] method leads to uniform EG growth with limited terrace restructuring on clean, low-miscut, chemically-mechanically polished SiC(0001) substrates [22], and often results in crescent-shaped terraces having small areas and low aspect ratios, as shown in Fig. 2. Fig. 2b shows details of the topographic structure produced by the FTG process at 1900 °C on the surface of low-miscut SiC(0001), imaged by AFM, and the corresponding phase image (Fig. 2c) shows uniform contrast. We have found that this terrace topography, together with the near-equilibrium FTG environment, supports more isotropic carbon diffusion compared to parallel, linear terraces, thus reducing the tendency to form extended bilayer ribbons. Annealing samples at T > 1800 °C with two SiC(0001) surfaces arranged face-to-face [22,23] results in uncontrolled step-bunching of the terraces (see Supplement Figs. S2a and b). This large change in substrate topography may be produced by the vapor phase transfer of molecules between the facing samples. Under similar conditions, but annealing the sample facing Ar background gas, it has been shown elsewhere that sub-µm scale pits are likely to develop on low-miscut SiC substrates [24] (see Supplement Fig. S2c). Our results show that FTG confinement reduces structural disorder due to pitting of the SiC surface for low-miscut substrates. Reduced mobility in EG transport has been correlated with the frequency of pitting [24] and with the size and height of underlying SiC terraces [20,25].

3.2. Confocal laser scanning microscopy

On sample A, the confocal laser scanning microscopy (CLSM) shows a nearly uninterrupted monolayer with only a few multilayer inclusions, which appear as small irregularly-shaped bright spots or ribbons in reflective confocal microscope images (see Fig. 3a and Supplement Figs. S2d and e). Note the large fiducial marker in the upper right. On sample B, bilayer ribbons and small patches of buffer layer are more common in some regions (Fig. 3b), but still occupy a small percentage of the sample surface. Sample B has low terrace topography, but the terraces are wider and more irregular in some areas (Supplement Fig. S1) indicating isolated step bunching. While C-face SiC processed with a graphite cap is reported to develop long graphene ribbons [21], we find that both terrace step bunching and multilayer EG growth are much more limited by FTG growth on the Si-face under optimized growth conditions.

3.3. Raman microscopy

Raman spectroscopy is a powerful nondestructive technique used to characterize atomically thin graphene samples. The two-phonon G′ band of monolayer graphene can be well fit by a single Lorentzian. Furthermore, the position of the G′ band has been correlated to the strain in the conductive EG lattice [26–28]. Studies of graphene on SiC also have established that the G′ band has only a weak dependence on carrier density [29], that strain can change suddenly where the EG layer crosses a terrace edge [30], and that low and uniform strain is often related to improved transport [31]. Raman data were obtained in closely-spaced grids after transport devices were fabricated on the two samples. No visible D band was observed near 1350 cm⁻¹ in the Raman spectra with two different laser excitation wavelengths (Supplement Fig. S3) which indicates low-defect EG in both samples. Raman maps (see Methods) were generated for three large, well-separated regions in the device spanning the midline of sample A, across an area of ≈ 5 mm width (Inset in Fig. 4a). Cross-correlated data for the resulting spectra are shown in Fig. 4a. Of the Raman data collected from the three areas, nearly 99% of the G′ spectra (1178 points) are symmetric and are fit with a single Lorentzian. The fitted G′ line-widths are less than 40 cm⁻¹, ranging from 27.5 cm⁻¹ to 38.2 cm⁻¹, and the mean center position is (2729.7 ± 2.7) cm⁻¹, ranging from 2721.3 cm⁻¹ to 2737.5 cm⁻¹. These closely grouped results with narrow linewidths reveal an unprecedented uniformity for EG, since both strain and layer number variation can affect these fitted parameters. The mean linewidth value Γ_G' = (31.7 ± 1.4) cm⁻¹ may be compared to Γ_G' ≈ 25 cm⁻¹, ranging from 22 cm⁻¹ to 35 cm⁻¹, as reported recently [32] for exfoliated graphene on SiO₂ capped by hexagonal BN (h-BN).

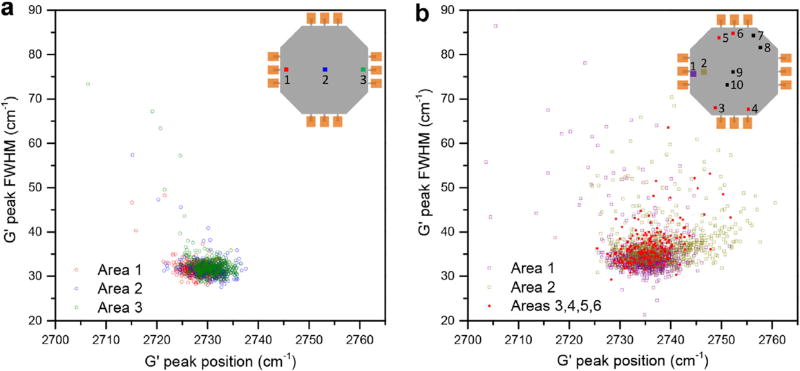
Fig. 4.

Raman G′ peak analysis for two octagonal devices. (a) Correlation between FWHM and peak position for G′ peaks collected from three areas in sample A, located as shown in the inset using red, blue, and green. (b) Correlation between FWHM and peak position for G′ peaks collected from six areas in sample B, located and identified by color as shown in the inset.

The Raman data from sample B (see Fig. 4b) in general have wider distributions, tending toward higher values of Γ_G′ and ω_G'. On the left side of the device we obtained a total of 1718 Raman spectra in two large areas ≈ 1 mm apart near the midline (areas 1 and 2 as seen in the inset of Fig. 4b). These data yield Γ_G' = (34.7 ± 4.6) cm⁻¹ and Γ_G' = (37.3 ± 5.2) cm⁻¹, with center positions ω_G' = (2735 ± 4.3) cm⁻¹ and ω_G' = (2738 ± 6.3) cm⁻¹, respectively for area 1 (purple) and area 2 (green). Additional Raman data were collected from eight widely distributed small areas (with less than 64 spectra per area) as shown in the inset of Fig. 4b (areas 3 to 10). While half of these areas (indicated in red) of sample B gave very homogeneous results, falling between the mean values for both ω_G′ and Γ_G′ from the two large areas, the other half indicated in black show no significant overlap (see Supplement Tables S1 and S2), and gave mostly values of Γ_G′ greater than 40 cm⁻¹. We have correlated this inhomogeneity observed in the Raman data from sample B with the positions of bilayer ribbons and buffer layer patches captured in confocal microscopy images like those shown in Fig. 3, and this will be explored in detail in a subsequent report. To summarize, in sample A we obtain narrower Raman G′ linewidths with very little spread in the position, while in sample B we find similar results but with inhomogeneous regions indicated by the Raman data. Neither sample shows linewidths as broad as were seen for the EG sample made by our earlier synthesis method (Fig. S4f).

4. Results and discussion

Inhomogeneous transport characteristics may result from substrate topography, variation in EG layer number [26,32,34,35], and/or the effect of strain [26–31,33,36]. Deconvolution of the effects of strain on transport in some EG samples can be problematic. This is illustrated by our earlier work where EG was grown at a lower temperature of 1630 °C in Ar background without FTG, on a substrate having a high miscut of ≈ 1.26° relative to the SiC(0001) basal plane. Low-energy electron microscopy (LEEM) data confirmed monolayer graphene on step-bunched, parallel terraces of 0.5 µm–2 µm width, and Raman mapping provided correlated data covering the same region (see Supplement Fig. S4). The G′ Raman band was fit to a Lorentzian function resulting in an average G′ peak position ω_G' = (2747.4 ± 1.7) cm⁻¹ for the sampled region of diameter 44 µm. The small standard deviation indicated excellent homogeneity at the spatial resolution (~2 µm) under which the data was collected. However, the G′ linewidth of Γ_G' = (63.8 ± 2.6) cm⁻¹ was quite broad compared to that seen in graphene produced by exfoliation from graphite [32,36] and in our samples A and B. Magnetotransport measurements in small Hall bar devices made from this earlier sample revealed low mobilities of μ < 1000 cm²/V at 1.5 K. While neither LEEM nor Raman captures the effects of terrace edges, the low mobility in this material may be linked to the broad, albeit uniform, G′ linewidth. The large linewidth could result from inhomogeneous strain at sub-micron scale [36] that is averaged within the 1 µm probe volume.

We correlate device transport in our FTG-grown EG with layer and strain homogeneity. Electrical measurements on samples A and B were made in a pumped liquid helium cryostat, and first will be correlated to our optical measurements, indicating the degree of inhomogeneous layer structure. Low-precision AC measurements were used to calculate the carrier density and mobility of the devices, and were repeated at various temperatures and current levels. We obtained precise QHE transport results for sample A with the original doping level obtained after removal of the Pd/Au protective layer, at n ≈ 2.4 × 10¹¹ cm⁻² (μ ≈ 4480 cm²/V). Fig. 5a shows magnetotransport characteristics for sample A at cryogenic temperatures.

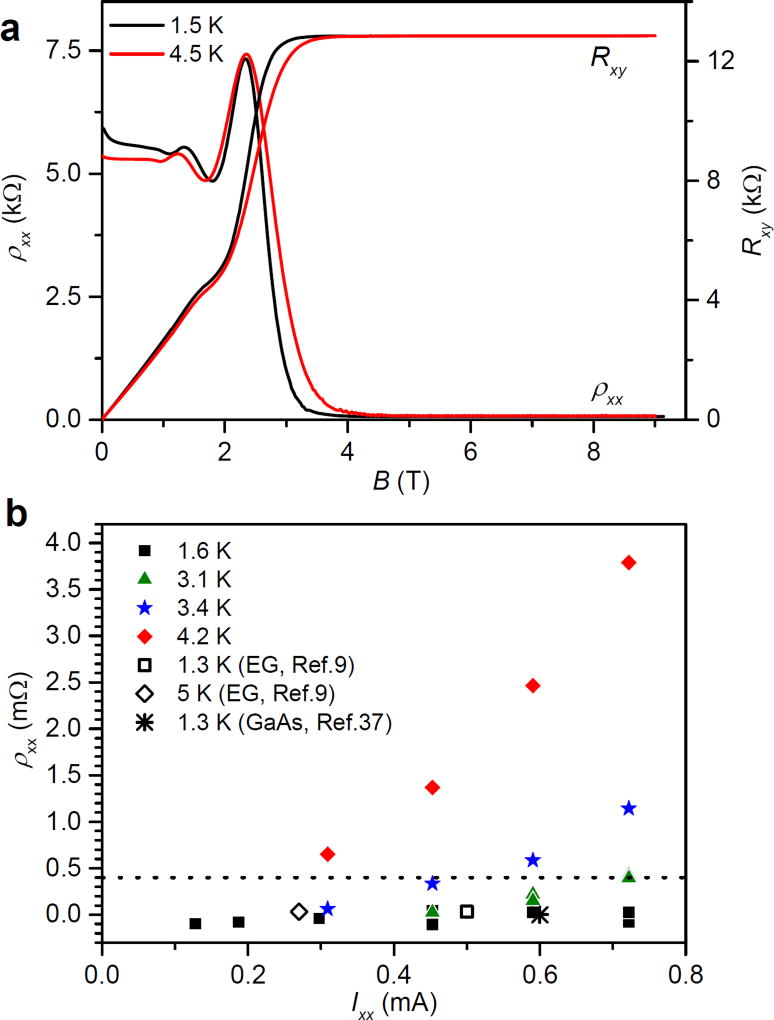
Fig. 5.

AC magnetotransport and DC precision measurements of ρ_xx of sample A in a perpendicular magnetic field B. (a) Transport characteristics with I_xx = 1 µA, n ≈ 2.4 × 10¹¹ cm⁻², and μ ≈ 4480 cm²/V for sample A. (b) Precision measurements of ρ_xx at 9 T as a function of source-drain DC current at 1.6 K, 3.1 K, 3.4 K and 4.2 K. Dashed line at ρ_xx = 0.4 mΩ indicates the degree of quantization sufficient to produce R_xy values within five parts in 10⁹ of the ideal quantized value, as described in the text. Results of earlier high-current studies of the QHE in graphene devices and in GaAs are included for comparison.

The hallmarks of the QHE in low-carrier-density EG are a broad plateau in the Hall resistance R_xy with conventional value $\frac{h}{2e^2}=\mathrm{12\; 906.4035}\mathrm{\Omega }$ (see Fig. 5a) and near-zero longitudinal resistivity ρ_xx. The strength of this QHE plateau at high current and temperature is enhanced at low perpendicular magnetic field strengths by the √B dependence of the Landau level energies, and by field-dependent charge transfer from donors in the SiC substrate and doping layer [8]. The presently used, commercial GaAs devices are rarely capable of sustaining precise QHE measurements at currents above 0.2 mA, and higher currents can exceed the range of most state-of-the-art metrological instruments used to measure R_xy. For sample A, we used two methods to obtain sensitive characterization of QHE device performance for higher current levels, with the first based on the increase in longitudinal resistivity ρ_xx. Values of the longitudinal resistivity ρ_xx were measured at four temperatures between 1.6 K and 4.2 K over a wide range of source-drain current (0.116 mA–0.72 mA), as shown in Fig. 5b. With an applied field of B = 9 T, zero dissipation is observed at 1.6 K for the full range of current up to I_xx ≈ 0.72 mA, and possibly at higher currents, but this could not be verified with the present apparatus (Supplement Fig. S5a). These results exceed the highest critical currents reported to date in graphene [9] (0.5 mA) or GaAs heterostructures [37] (0.6 mA).

Near the onset of thermally-activated dissipation [10,38], a linear relationship is generally observed between the deviation of the Hall resistance ΔR_xy from the quantized value $(\frac{h}{2e^2})$ and the non-zero value of ρ_xx. A specialized two-terminal cryogenic current comparator (CCC) bridge [39] was employed to measure values of R_xy at T = 1.6 K and T = 4.2 K against a precision 100 kΩ standard resistor at current levels I_xx = 0.3 mA, 0.45 mA, 0.6 mA and 0.72 mA. While GaAs-based QHE calibration of the 100 kΩ standard must be conducted at lower current levels and is thus less precise, the small differences measured for sample A at these two temperatures can be obtained with an uncertainty of better than 5 × 10⁻⁹ in R_xy. Plotted against values of the longitudinal resistance ρ_xx measured at 4.2 K for the same current levels, the deviation ΔR_xy = R_xy (4.2 K) − R_xy (1.6 K) yields a slope ΔR_xy/ρ_xx (4.2 K) ≈ 0.164 ± 0.01 (see Supplement Fig. S5b). Thus, the accuracy of the QHE is maintained at the level of 5 × 10⁻⁹ in sample A up to I_xx ≈ 0.72 mA at T = 3.1 K and 9 T, where ρ_xx ≤ 0.4 mΩ is measured (as noted by the dashed line in Fig. 5b).

In our samples the adsorbed molecular doping layer acts as a gate, and it is possible to control the carrier concentration through this effect (see Supplement, section 7). The concentration of adsorbed dopants was tuned after the initial fabrication of sample B, first by exposure to vapor from concentrated HNO₃, followed by gentle heating of the sample in vacuum [19,40]. AC transport measurements were made on sample B at seven levels of carrier density, as shown in Fig. 6a and Fig. S7. Mobility in EG at low temperature is strongly dependent on carrier density, as demonstrated in sample B by the nearly inverse relationship between μ and n for n-type carrier concentrations below 3.0 × 10¹¹ cm⁻². Mobility of μ ≈ 3120 cm²/V is obtained in sample B at carrier density level of n₂ ≈ 1.8 × 10¹¹ cm⁻², compared to the mobility μ ≈ 4480 cm²/V at n ≈ 2.4 × 10¹¹ cm⁻² for sample A.

Fig. 6.

AC magnetotransport as a function of carrier density and DC precision QHE measurements of sample B. (a) Graph of mobility μ versus carrier density n for sample B, calculated from the device conductivity σ_xx = enμ and the slope of the Hall resistance R_xy(B). Starting at far left with low p-type doping (4.7 × 10¹⁰ cm⁻²) changes in n and μ were obtained by exposure to oxygen and heating the sample at increasing temperatures of 310 °C–333 °C in vacuum (see Supplement Fig. S7). Fitting of the data to an inverse function μ = a + b × (n−c)⁻¹ for n > 0 results in the dotted curve, showing an approximate inverse relation, and this fit is mirrored about n = 0 to show that the same relation may exist for p-type carriers. Inset: transport characteristics for very low n-type carrier density (n₀) identified by the blue circle. (b) Sample B transport characteristics for carrier density (n₁). (c) Sample B transport characteristics for higher carrier density (n₂). (d) Precise measurements of the deviation in the Hall resistance R_xy(B) plotted for the two levels of carrier density n₁ and n₂. Data for n₁ was taken at I_xx = 19.4 µA, while data for n₂ was taken at I_xx = 116 µA. The dependence on n and T is described in the text.

Despite the presence of inhomogeneous strain and layer number in some areas of sample B, the measured mobility for n₀ ≈ 0.9 × 10¹⁰ cm⁻² is μ ≈ 18760 cm²/V (see Supplement section 7). This confirms that high mobility can be maintained in EG in the presence of localized defects [24] if the density of these defects is not too high, and indicates that a 10 mm² area of sample B has very uniform carrier density at low temperature. For comparison, similar characteristics of μ and n have been reported in gated, high-quality EG [33] devices of <5 µm width. For those, the mobility was somewhat higher at carrier density n ≈ 2 × 10¹¹ cm⁻² ≈ (n₂) and was seen to decrease for values of n below ≈ 10¹¹ cm⁻², an effect that we did not observe in the FTG sample B for much lower carrier densities. Exfoliated graphene on h-BN [36] has exhibited mobilities up to four times what we measure at similar low carrier densities, and the authors did not report any decrease in the mobility at lower carrier density. More generally, the QHE in the millimeter-size EG samples described here far surpasses earlier results that we obtained using similar-scale CVD graphene [41].

Precise values of R_xy in sample B were measured at doping levels indicated by (n₁) and (n₂) shown in Fig. 6a, with magnetotransport data given in Fig. 6 (a–d). These measurements were made near the highest levels of current for which full quantization was maintained for each carrier density. At these current levels, I_xx(n₁) ≈ 0.0194 mA and I_xx(n₂) ≈ 0.116 mA, conventional CCC measurements of R_xy could be based on 100 Ω standard resistors precisely calibrated against a NIST GaAs-based QHE standard. For the lower carrier density n₁ and T ≈ 1.7 K, the value of R_xy differed from $\frac{h}{2e^2}$ by less than the measurement uncertainty of ±5 × 10⁻⁹ within the range 3 T < B < 9 T (see Fig. 6d). For similar conditions but with T = 3.0 K, the value measured for R_xy differed from the ideal value by about five parts in 10⁸ near B = 6 T, with increased variation from the ideal value at lower and higher field. When sample B was tuned to higher carrier density (n₂), precise quantization was maintained over the range 7.5 T < B < 9 T for higher measurement current of I_xx = 0.116 mA and T = 2.8 K. For the same range of B and I_xx = 0.116 mA, the value of R_xy showed slight loss of quantization (ΔR_xy/R_xy ≈ 1 × 10⁻⁸) for T = 5.1 K (Fig. 6d).

While our FTG graphene is produced on low-miscut SiC(0001) by annealing at 1900 °C in a near-equilibrium growth environment, improved QHE transport under relaxed conditions has also been reported in graphene which was grown on higher-miscut SiC(0001) by a hydrogen-supported CVD process [9], where step bunching of SiC appears to be strongly suppressed. Step-bunching and bilayer regions are sources of scattering, and our results suggest that these regions may contribute to non-uniform strain in the EG layer. In semiconductor quantum Hall systems, the plateaus in R_xy are centered at magnetic field values B_c = enR_H, where n is the density of conducting electrons and R_H is equal to h/ie² with i taking on integer values, and the width of the plateau for a given quantum number i is related to the level of dissipation in the device. However, in EG devices the i = 2 plateau can extend to very high values of B due to charge transfer at the substrate/graphene interface, which is thought to be proportional to B for some range of high magnetic field [8]. For carrier densities where the transition from the i = 6 to i = 2 plateau region is evident in EG magnetotransport, we can estimate the “half-width” of the $R_{\mathit{\text{xy}}}=\frac{h}{2e^2}$ plateau by the difference between the onset field B₀ and the field B_c where the extrapolated low field resistance reaches $\frac{h}{2e^2}$, ΔB = B_c − B₀. The onset field B₀ is defined as the field where R_xy(B₀) = 0.99 R_xy(B_c). The half-width ΔB is smaller in sample B than in sample A for similar levels of carrier density n ≈ 2 × 10¹¹ cm⁻² (see supplement Section 8), indicating that more dissipation is present in sample B than in sample A for similar values of magnetic field and temperature, consistent with the much lower critical current observed in sample B.

5. Conclusion

In conclusion, our observations for sample A clearly show that desirable magnetotransport properties are correlated with low and uniform strain in EG on SiC(0001) substrates. The uniform Raman G′ band characteristics we observe compare favorably with those described in earlier reports [26–31] and provide support for the first example of EG with highly uniform strain at millimeter scale. The small G′ FWHM and the narrow distribution of its position in sample A suggest reduced strain variation at the submicron scale [36]. In sample B, where bilayer inclusions are more common and strain is inhomogeneous in some areas, transport characteristics such as the lower critical current suggest greater dissipation, compared to sample A. However, our results indicate that the areas of homogeneous EG layer number and strain in sample B are sufficient for efficient millimeter-scale transport, as is evident from the QHE results over an extended range of magnetic field and by mobility exceeding 18700 cm²/Vs for very low carrier density n₀ ≈ 1 × 10¹⁰ cm⁻². While a better understanding of strain inhomogeneity in monolayer EG is still needed, our results indicate that uniform lattice strain and reduced topographic variation contribute to improved 2D quantized conductance at elevated current and temperature, and may provide direction for further advances in wafer-scale device fabrication.

6. Methods

Raman spectra were acquired under ambient conditions with a Renishaw InVia confocal Raman microscope equipped with 514.5 nm (2.41 eV) and 632.8 nm (1.96 eV) excitation lasers and an 1800 lines/mm grating while operating in 180° backscattering geometry. A 50× objective was used to focus the excitation laser light to an approximately 1 µm spot on the samples. Raman mapping measurements were performed using 514.5 nm excitation by raster scanning rectangular areas with a step size of 1 µm and collecting the Raman G′ peak region with an exposure time of 10 s for each point. Raman maps were generated by fitting the spectra with a single Lorentzian peak and plotting the fitting parameters of FWHM and peak position at each pixel.

For initial transport characterization, four lock-in amplifiers monitored the longitudinal current I_xx supplied at 13 Hz and three voltages developed in the device while we swept the perpendicular magnetic field strength B. We measured the Hall resistance R_xy = V_xy/I_xx across the central pair of contacts (Fig. S6). Longitudinal resistivity ρ_xx was derived from the average resistance value measured across the other four symmetric contacts (4,6,10,12 in Fig. S6), scaled by the ratio of width to length (αw/L = α × 5.6 mm/1.8 mm) separating these terminals, where α = 1.3 is a geometrical factor estimated from the DC transport simulation of a thin film conductor with the same semi-octagonal shape as our devices (Fig. S6). The high precision longitudinal resistivity was measured between the central pair of contacts (5, 11 in Fig. S6) used to determine R_xy and one set of adjacent contacts, scaled by the ratio αw/L = α × 5.6mm/0.9 mm, using a nanovolt meter (EM Electronics model N11) and recorded automatically using an Agilent 3458A DMM. Periodically reversed current was supplied by a battery-powered ramping voltage source. CCC measurements were made as described in Ref. [39]. Estimation of carrier density and mobility were detailed in the supplement information, section 7.