Skip to main content
. Author manuscript; available in PMC: 2018 Sep 15.
Published in final edited form as: Clin Cancer Res. 2017 May 24;23(18):5469–5479. doi: 10.1158/1078-0432.CCR-16-3277

Figure 1.

Figure 1

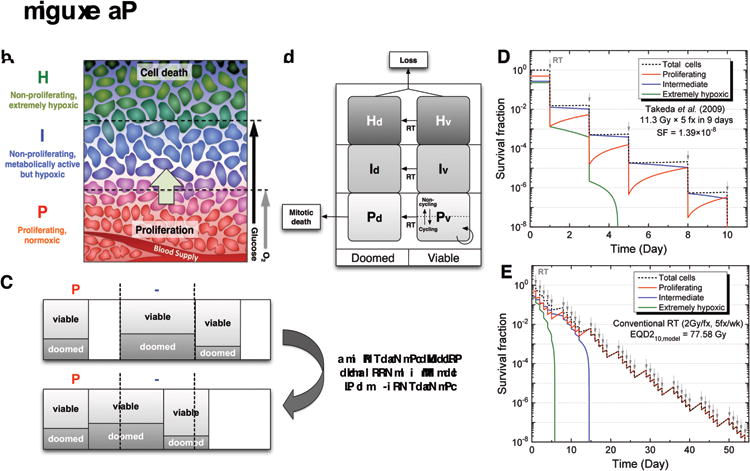
Schematic diagrams of the state-driven tumor response model and the estimation of equivalent dose for non-standard fractionations based on the model. (A) Three different compartments in the model based on the microenvironment of a tumor with respect to the blood supply. Due to a limited blood supply, there are limited supplies of oxygen and the key nutrient, glucose. Cells with adequate oxygen and glucose are actively proliferating, while cells distant from vessels are starving and dying. In the model, theses populations of cells were simplified into three different compartments (P, I, and H), which have different levels of proliferation, hypoxia, cell death, and radiosensitivity. Note that uniform levels of glucose and O2 were assumed for each compartment. (B) After radiation therapy begins, a fraction of cells in each compartment becomes doomed depending on compartment-specific radiosensitivity and die in an attempt of mitosis in the proliferative P-compartment. (C) Re-compartmentalization and reoxygenation pattern after the post-mitotic death of doomed cells in the P-compartment. As long as cells are available, the P-compartment “tops up” at each time step. (D-E) An example of EQD210,model estimation based on two separate simulations, in which the fraction size-dependent radiosensitivity, proliferation, and hypoxia effects are incorporated: (D) after the cell survival fraction was estimated for a SBRT regimen (11.3Gy×5fxs) from Takeda et al. (30), (E) a conventional 2 Gy-fractionation was simulated until the same level of survival fraction was achieved, resulting in EQD2 α/β,model. (Figures A, B, and C are used with permission). Panel A reprinted from Jeong J, Deasy JO. Modeling the relationship between fluorodeoxyglucose uptake and tumor radioresistance as a function of the tumor microenvironment. Comput Math Methods Med 2014;2014:847162. Panels B and C reprinted from Jeong J, Shoghi KI, Deasy JO. Modelling the interplay between hypoxia and proliferation in radiotherapy tumour response. Phys Med Biol 2013;58:4897–919. © Institute of Physics and Engineering in Medicine. Reproduced by permission of IOP Publishing. All rights reserved.