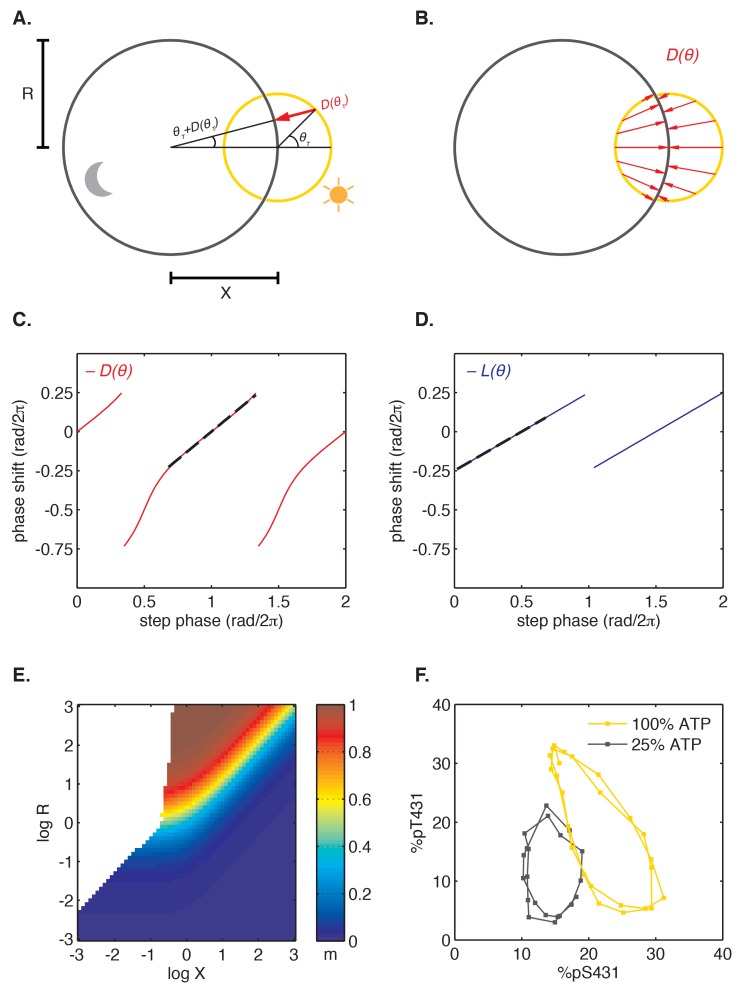
Figure 6. Nearly linear step response functions can arise from the relative geometry of day and night limit cycles.

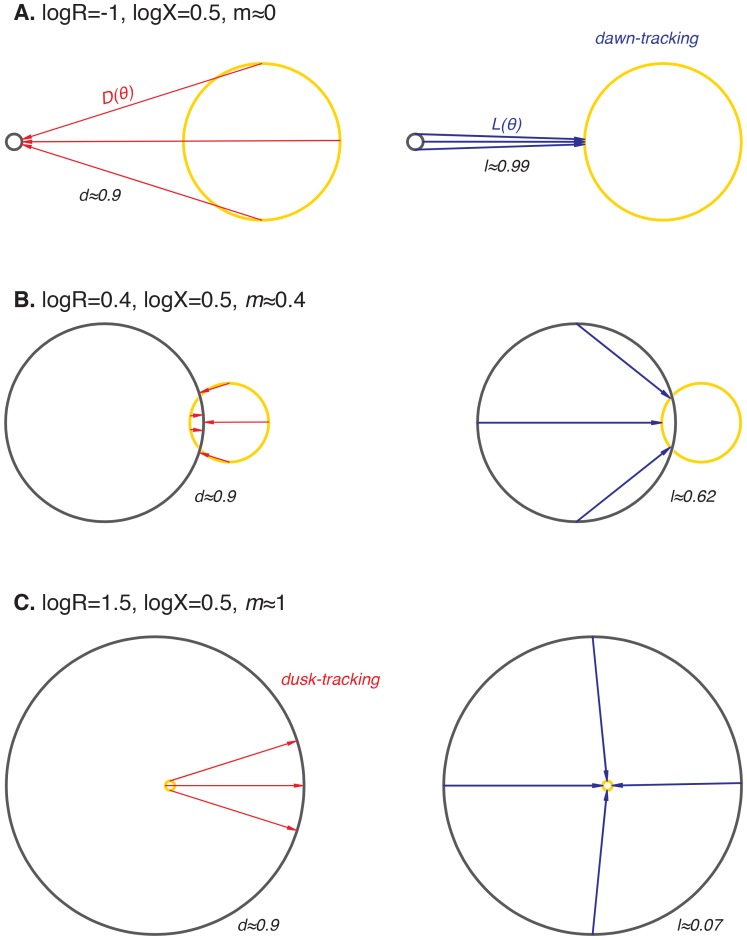
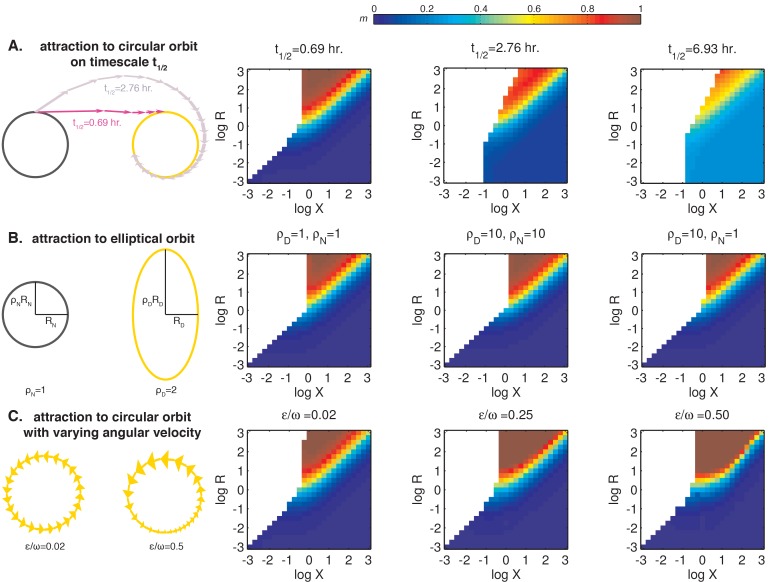
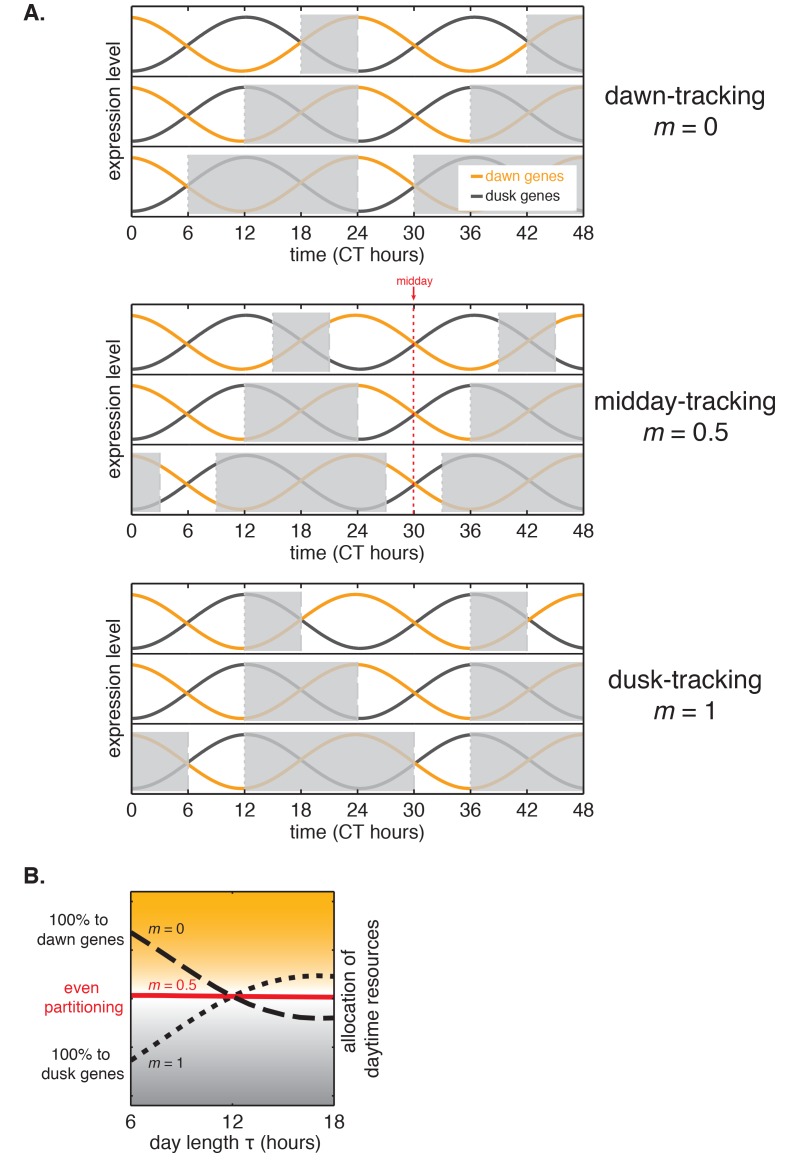
(A) Geometric model of oscillator phase resetting. During the day, the oscillator runs with constant angular velocity along the daytime orbit (yellow), which has unit radius and is centered at the origin. At dusk, the oscillator transits to the nighttime orbit (black), which has radius R and is displaced from the daytime orbit by X units. In the limit where the nighttime orbit is strongly radially attracting, we can approximate oscillator response to the light-dark transition ($D\left({\theta }_{\tau }\right)$, red arrow) as an instantaneous jump from phase ${\theta }_{\tau }$ on the daytime orbit toward the center of the nighttime cycle, resulting in phase ${\theta }_{\tau }+D\left({\theta }_{\tau }\right)$ on the night orbit. (B) Simulation of oscillator phase shifts due to light-dark transitions at different phases on the day orbit (red arrows) for R = 2, X = 2. For geometries with X ≈ R, phase angles on the day orbit are compressed to an arc on the night limit cycle that subtends a smaller angle. See Computational methods for calculation details. (C and D) Simulations of $L\left(\theta \right)$ and $D\left(\theta \right)$ step response functions arising from the geometric arrangement of day and night cycles in (B). Linear regions of $L\left(\theta \right)$ and $D\left(\theta \right)$ are marked with black dashes. See Computational methods and Appendix 1 for calculation details. (E) Heat map of the slope m of the approximately linear relationship between entrained phase and day length, plotted as a function of X and R. In white regions, the oscillator does not entrain stably or the oscillator does not show linear scaling of phase with day length. Slope determined from simulations of oscillator entrainment to 24 hr driving cycles of day length τ = 6–18 hr. See Computational methods for details. (F) Limit cycles traversed by the KaiABC oscillator in vitro in metabolic conditions mimicking day (yellow, [ATP]/([ATP]+[ADP]) ≈ 100%) and night (black, [ATP]/([ATP]+[ADP]) ≈ 25%). Oscillations in KaiC phosphorylation on Ser431 and Thr432 are replotted from data in Phong et al. (2013).

DOI: http://dx.doi.org/10.7554/eLife.23539.036

Figure 6—figure supplement 1. Illustrations of limit cycle geometries that give rise to step-response functions $L\left(\theta \right)$ and $D\left(\theta \right)$ with different slopes, resulting in dusk-, dawn-, or midday-tracking entrainment.

In all schematics, the day orbit (yellow) is centered at the origin and has radius 1. The night orbit (black) has radius R and is displaced from the day orbit ($\log X=0.5)$ units). Light-dark ($D\left(\theta \right)$) and dark-light ($L\left(\theta \right)$) transitions are indicated by red and blue arrows, respectively. (A) When the night cycle is much smaller than the day cycle (R << 1), both dawn and dusk are strongly resetting (l≈1, d≈1). Because all phases on the night orbit are mapped to a small range of phases on the day orbit, oscillator phase at dawn is independent of day length during entrainment (m≈0, dawn-tracking). (B) When the sizes of day and night orbits are comparable (R ≈ 1), the slopes of $L\left(\theta \right)$ and $D\left(\theta \right)$ depend on the fine-tuned arrangement of the orbits. Generally, both $L\left(\theta \right)$ and $D\left(\theta \right)$ exert entraining effects in this regime (l > 0, d > 0). The slope of entrained phase with day length depends on both l and d, according to $m(l,d)=d(1-l)/(d+l-ld)$ (see Figure 4—figure supplement 3 and Appendix 1). (C) When the night cycle is much bigger than the day cycle (R >> 1), dusk is strongly resetting, but dawn transitions have little effect on clock phase (l≈0, d≈1). Entrainment to repeated light-dark cycles maps clock phases on the night orbit to a shrinking range of angles, leading to dusk-tracking entrainment (m≈1).

DOI: http://dx.doi.org/10.7554/eLife.23539.037

Figure 6—figure supplement 2. The relative size (R) and center-to-center distance (X) of day and night limit cycles are major determinants of entrained behavior.

Heat maps of m, the slope of the approximately linear relationship between entrained phase and day length, are plotted as a function of X and R on the same color scale as in Figure 6E. See Computational methods for simulation details. (A) Entrainment simulations with non-instantaneous jumps between day and night limit cycles. The half-times $t_{1/2}$ for transition between the circular orbits are indicated above the heat maps. Schematic on the left illustrates the evolution of the oscillator from a point on the night limit cycle to the day limit cycle in two scenarios with different relaxation times. Each arrow represents the displacement of the oscillator in 1 hr. (B) Entrainment simulations for day and night limit cycles of varying ellipticity. The ratios of the major axis length to the minor axis length of the day and night orbits (ρ_D and ρ_N) are indicated above the heatmaps. In these simulations, we considered strongly attracting orbits ($t_{1/2}=0.069$ hr) oriented with their major axes perpendicular to the separation between their centers. (C) Entrainment simulations for day and night limit cycles with non-constant angular velocities. In these simulations, we considered circular orbits for both day and night limit cycles. Orbit attraction timescale was set to $t_{1/2}=0.69$ hours. The variability in angular speed $\dot{\theta }$throughout the cycle is given by ${\displaystyle \stackrel{.}{\theta }=\omega \left(1+\frac{\epsilon }{\omega }\sin \omega t\right)}$. Schematic on the left illustrates the evolution of the oscillator along day limit cycle in two scenarios with different values of $\frac{\epsilon }{\omega }$. Each arrow represents the displacement of the oscillator in 1 hr; size of the arrowheads illustrates changes in angular velocity throughout the cycle (not to scale).

DOI: http://dx.doi.org/10.7554/eLife.23539.038

Figure 6—figure supplement 3. Interpretation of m, the slope of the approximately linear relationship between entrained phase and day length.

(A) The value of m dictates whether the circadian rhythm aligns to dawn (m = 0), dusk (m = 1), or an intermediate point of the day-night cycle (e.g. midday for m = 0.5). Orange and gray curves show sinusoidal fits to average transcriptional profiles of dawn and dusk genes in S. elongatus based on data from Vijayan et al. (2009). Gray bars indicate night in light-dark cycles for m = 0, 0.5, and 1. (B) Tracking midday as the day length varies may be a strategy to balance biosynthetic resources between dawn and dusk transcriptional programs. For each value of m, the corresponding curve shows a numerical estimate of the relative fraction of dusk and dawn gene expression that occurs during the day in S. elongatus (arbitrary units, see Computational methods).

DOI: http://dx.doi.org/10.7554/eLife.23539.039