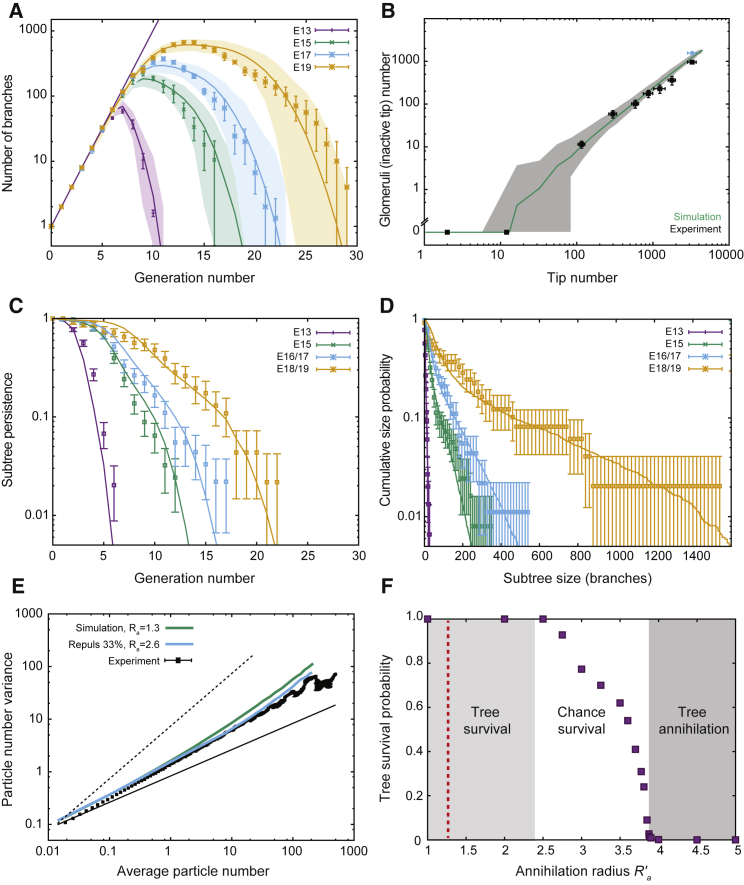
Figure 7.
Branching and Annihilating Random Walks Can Reproduce Quantitatively the Detailed Properties of Kidney
(A) Using the radius of termination Ra as the only free parameter, the model predicts well the number of segments per generation at different time points of embryo development (E13, E15, E17, and E19 in purple, green, blue, and orange, respectively).
(B) Inactive tip number (assessed indirectly via glomeruli staining from [Sampogna et al., 2015] in black, or glomeruli counting via a method of acid maturation from [Cebrian et al., 2014] in blue) versus total number of tips, displaying a power law after a phase of purely symmetric branching, predicted by the model (green).
(C) Subtree persistence at different developmental time points (squares) compared to the model (lines).
(D) Cumulative subtree size distribution at different developmental time points (squares) compared to the model (lines).
(E) Variance (y axis) versus the average (x axis) duct volume in a box of size L (experiments in black) in kidney, showing an exponent larger than 1/2 (thin and dashed black line represent exponents of 1/2 and 1, respectively), indicative of giant number fluctuations. The green and blue lines are predictions from default model (no repulsion, R′a = 0.25), and model with repulsion (fr = 0.33, R′a = 0.5).
(F) Tree survival probability versus termination radius, showing a phase transition above which kidney systematically become fully annihilated. Red dashed line shows the best-fit value of Ra used in (A)–(D). Shaded areas represent 95% confidence intervals, and error bars represent mean and SEM.
Lines in (A)–(D) are model predictions, using the parameter R′a fitted from Figure 6D. See also Figure S7 and Movies S2 and S3.