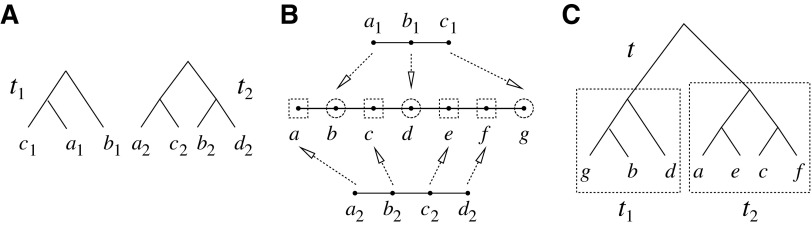
FIG. 8.
Composition of two trees t1 and t2 of sizes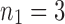 
and 
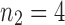to obtain a tree t of size 
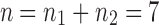. (A) Trees t1 and t2, with leaves labeled by 
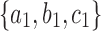and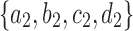 
. As in Section 2.1, we impose without loss of generality a linear order 
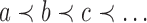for the leaves of a tree; here, we have 
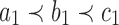and 
. (B) Relabeling of trees t1 and t2. After relabeling, t1 and t2 have leaves labeled in the set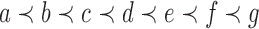 
of size 
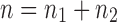. For the relabeling procedure, we choose (dotted circles) n1 elements among the n possible new labels 
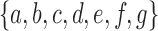. There are exactly 
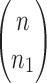different choices. The chosen elements relabel t1, whereas the elements not selected (dotted squares) relabel t2. With respect to the order 
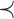, the ith label of t1 is assigned the label determined by the ith circle. Similarly, the ith label of t2 is assigned the label determined by the ith square. (C) After relabeling t1 and t2, the new tree t is obtained by appending t1 and t2 to a shared root node. Starting with trees t1 and t2 in (A), the same procedure can generate 
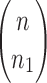different trees t, one for each possible choice of the n1 elements (dotted circles) among the n new labels. The only exception is when 
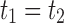, for which the 
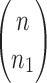relabelings generate each tree exactly twice.