Computer-aided classification of sickle cell retinopathy using quantitative features in optical coherence tomography angiography

Abstract

As a new optical coherence tomography (OCT) imaging modality, there is no standardized quantitative interpretation of OCT angiography (OCTA) characteristics of sickle cell retinopathy (SCR). This study is to demonstrate computer-aided SCR classification using quantitative OCTA features, i.e., blood vessel tortuosity (BVT), blood vessel diameter (BVD), vessel perimeter index (VPI), foveal avascular zone (FAZ) area, FAZ contour irregularity, parafoveal avascular density (PAD). It was observed that combined features show improved classification performance, compared to single feature. Three classifiers, including support vector machine (SVM), k-nearest neighbor (KNN) algorithm, and discriminant analysis, were evaluated. Sensitivity, specificity, and accuracy were quantified to assess the performance of each classifier. For SCR vs. control classification, all three classifiers performed well with an average accuracy of 95% using the six quantitative OCTA features. For mild vs. severe stage retinopathy classification, SVM shows better (97% accuracy) performance, compared to KNN algorithm (95% accuracy) and discriminant analysis (88% accuracy).

1. Introduction

Sickle Cell Disease (SCD), one of the most prevalent inherited blood disorders, is caused by a mutation in the $\beta$-globin gene [1] which results in the deformation of erythrocytes from a disc to a “sickle”- shape during periods of stress and ischemia [2]. Consequently, an individual with SCD suffers from microvascular occlusions in various parts of the body, including the retina [3]. According to The American Society of Hematology reports [1], SCD occurs in approximately 300,000 births annually in the world and around 1 in every 365 African-American births in the United States. Although SCD is mostly seen in malaria-endemic parts of the world predominantly in Africa, South Asia, and the Middle East, an estimated 100,000 people are also affected by SCD in the United States in 2016, making it one of the most common genetic disorders worldwide [1].

Sickle cell retinopathy (SCR) results from the microvascular occlusions induced by sickle-shaped erythrocytes in the retina [4]. It is considered as the major ocular manifestation of SCD to produce visual impairment and blindness [5]. The anatomical changes in the retina are highly associated with the disease progression. It is observed that the pathological course of SCR is extremely variable, encompasses many stages ranging from proliferative to non-proliferative changes [2]. The quantitative assessment of the anatomical changes may be used as a biomarker of SCR severity. Early in the disease process, ophthalmoscopy may show dilated [6, 7] and tortuous [6, 8, 9] retinal vessels along with a foveal depression sign [10] in patients with SCR. The spectral domain optical coherence tomography (SDOCT) imaging of SCR has shown outer retinal thinning and macular splaying [11] when the clinical exam shows minimal findings and the patient has excellent visual acuity. Retinal neovascularization, retinal detachment as well as capillary dropout occur as SCR advances [2]. These features closely related to physiological changes in retinal vasculature can be quantified by calculating fractal dimension (FD) [12, 13], a potential biomarker for SCR disease detection [14–16].

Traditional fluorescein angiography (FA) [17] and recently emerging optical coherence tomography angiography (OCTA) [18] can be used for clinical evaluation of SCR and other diseases. OCTA has been recently used for quantitative assessment of retinal vascular structures [19–24] as it allows depth-resolved visualization of multiple retinal layers with high resolution, and therefore is more sensitive than traditional FA in detecting retinal diseases [18]. Computer-aided OCTA classification is desirable to help classifying SCR patients during screening and for telemedicine evaluations. As a new OCT imaging modality, there is no standardized quantitative interpretation of OCTA characteristics of SCR. In comparison with diabetic retinopathy (DR) and age-related macular degeneration (AMD), the SCR population is relatively small. While there are limited numbers of SCR experts within urban hospitals and well developed countries, many SCD patients in other regions are unable to receive routine SCR screening to enable effective prevention of SCR-related visual impairment. In coordination with affordable internet technology, computer-aided OCTA screening and classification would foster telemedicine to reduce healthcare disparities and improve access to eye care for patients in rural and underserved areas.

This study was performed to explore computer-aided detection and classification of SCR based on quantitative characteristics in OCTA images. In our previous work [25], we have conducted a comprehensive analysis of OCTA images to derive six OCTA biomarkers, including blood vessel tortuosity (BVT), blood vessel diameter (BVD), vessel perimeter index (VPI), foveal avascular zone (FAZ) area, FAZ contour irregularity and parafoveal avascular density (PAD). In this study, these six demonstrated OCTA parameters were used as feature vectors to classify SCR images using machine learning techniques. Three classifiers, i.e., SVM (support vector machine), KNN (k-nearest neighbor) algorithm and discriminant analysis were used for classifying SCR vs. control and mild SCR vs. severe SCR. It was observed that classification sensitivity, specificity, and accuracy can be improved due to the comprehensive involvements of multiple OCTA features compared to single feature.

2. Methods

This section describes the algorithms for computer-aided classification of OCTA images. The core steps are briefly illustrated in Fig. 1, and technical details are explained in following sections.

Fig. 1.

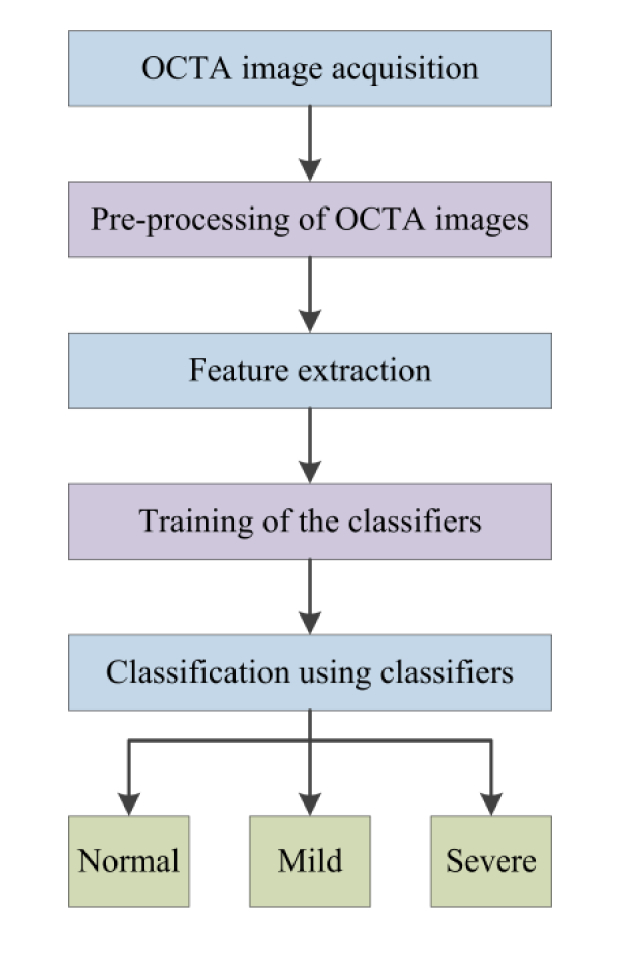
Flow chart of the procedures for automated classification.

2.1 OCTA image acquisition

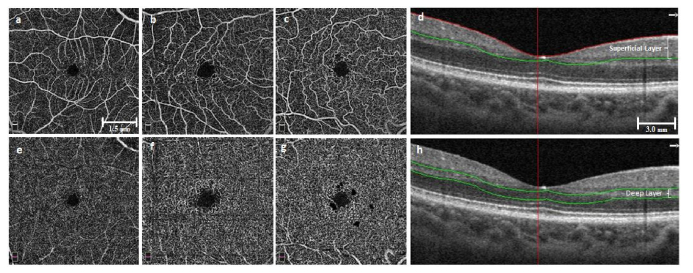
This study was approved by the Institutional Review Board of the University of Illinois at Chicago and was in compliance with the ethical standards stated in the Declaration of Helsinki. The SCD patients were recruited from University of Illinois at Chicago (UIC) Retinal Clinic. All patients had undergone a complete anterior and dilated posterior segment examination (JIL). The degree of SCR was graded according to the Goldberg classification. The OCTA data set consisted of 35 SCD patients (12 male and 23 female, 35 African Americans) and 14 control subjects (11 males, 3 female, 5 African Americans). It is known that sickle cell disease predominantly affects African American [26]. Therefore, all patients for this SCR study were African Americans. Among the 35 SCR patients, the majority (N = 29) had Stage II sickle retinopathy, and the remaining (N = 6) had Stage III. For simplifying the classification process, we defined the stage II and III as mild and severe stage SCR, respectively. The mean age of the SCD patients was 40 years (range 24 to 64), while for control it was 37 years (range 25 to 71). OCTA images of both eyes (OS and OD) were analyzed, so the database consisted of 70 SCR eyes and 28 control eyes. The subjects of the control group were chosen based on their previous ocular history, absence of any systemic diseases or any visual symptoms; a normal-appearing retina on clinical examination; and a normal reflectance OCT of the macula. Figure 2 illustrates representative OCTA images of superficial and deep layers for control and SCR (mild and severe) eyes.

Fig. 2.

Representative OCTA images of superficial (a-c) and deep (e-g) layers. (a,e) Control eyes, (b,f) Mild stage SCR, (c,g) Severe stage SCR. (d) and (h) show corresponding sample B-scan OCT images with segmented superficial and deep layers respectively. (a-c) and (e-g) have same scale bar. (d) and (h) have same scale bar.

SD-OCT data were acquired using an ANGIOVUE SD-OCT angiography system (Optovue, Fremont, CA, USA), with a 70-KHz A-scan rate, an axial resolution of ∼5 μm and a lateral resolution of ∼15 μm. All the OCTA images had field of view (FOV) of 6 mm × 6 mm. We exported the OCT angiography images from the software ReVue (Optovue, Fremont, CA, USA) and used custom-developed MATLAB (Mathworks, Natick, MA, USA.) procedures with graphical user interface (GUI) for further image analysis, feature extraction and image classification.

2.2 Pre-processing of OCTA images

For vascular and foveal feature extraction, we used OCTA images (304 pixels × 304 pixels) with a dimension of 6 mm × 6 mm. Different images usually have different intensity and contrast levels because they are captured in different times with variable light settings by the clinician, so we normalized all the OCTA images to a standard window level based on the maximum and minimum intensity values.

2.3 Feature extraction

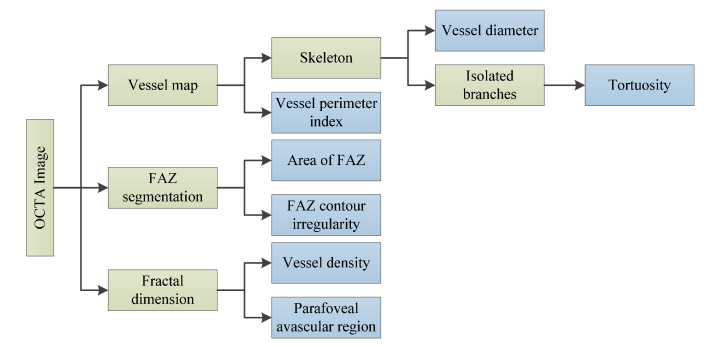
We used 6 parameters, including BVT, BVD, VPI, FAZ area, FAZ contour irregularity and PAD as feature vectors to classify the OCTA images. While analyzing avascular density in OCTAs, we considered densities in three circular parafoveal regions of diameter 2 mm, 4 mm and 6 mm and four parafoveal sectors, namely, nasal (N), superior (S), temporal (T), and inferior (I) of a circular zone of diameter 6 mm.

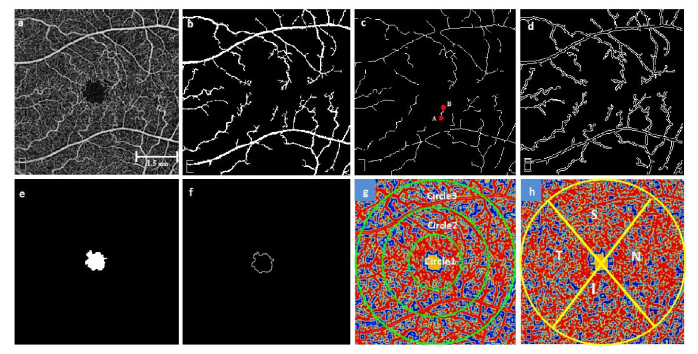
Figure 3 shows a flowchart providing an overview of the processes involved in extracting feature vectors and Fig. 4 illustrates the representative images of feature extraction. The rationale of each of these six OCTA parameters has been described in our recent publication [25]. Table 1 summarizes the demonstrated quantitative OCTA features.

Fig. 3.

A flow chart showing various features extracted from OCTA image.

Fig. 4.

Representative images for illustrating the feature extraction (a) OCTA raw image, (b) Segmented large blood vessel map, (c) Skeletonized blood vessels branches with identified endpoints (for a random vessel branch, A and B endpoints are shown with red dots), (d) Vessel perimeter map, (e) Segmented avascular region, (f) FAZ contour, (g,h) Contour maps created with normalized values of local fractal dimension in superficial and deep layers respectively. (g) Circular zones of diameter 2, 4 and 6mm, (h) Nasal, Superior, Temporal and Inferior regions.

Table 1. Methodology for extracting features.

Features	Approaches for feature extraction
BVT	Global thresholding, morphological functions and FD classification used for creating the vessel map (Fig. 4(b)). Vessel map skeletonized and each branch identified with endpoints (Fig. 4(c)). Distance metric used for measuring tortuosity [27]. $\text{Euclidean distance}=\sqrt{{({\text{x}}_1-{\text{x}}_2)}^2+{({\text{y}}_1-{\text{y}}_2)}^2}$(1) $\text{Geodesic distance}=\underset{{\text{t}}_0}{\overset{{\text{t}}_1}{{\displaystyle \int }}}\sqrt{{\left(\frac{\text{dx}(\text{t})}{\text{dt}}\right)}^2+{\left(\frac{\text{dy}(\text{t})}{\text{dt}}\right)}^2}\text{ dt}$(2) $\text{Tortuosity}=\frac{1}{\text{n}}{\displaystyle \sum }_{\text{i}=1}^{\text{n}}\left(\frac{\text{Geodesic distance of a vessel branch i}}{\text{Euclidean distance of a vessel branch i}}\right)$(3) where i is the ith branch and n is the number of branch.
BVD	Ratio of vascular area (calculated from Fig. 4(b)) and vascular length (calculated from Fig. 4(c)) was defined as the mean diameter of the blood vessels [23]. $Mean vessel width=\frac{{{\displaystyle \sum }}_{i=1,\hspace{0.17em}j=1}^{n}B\left(i,\hspace{0.17em}j\right) }{{{\displaystyle \sum }}_{i=1,\hspace{0.17em}j=1}^{n}S\left(i,\hspace{0.17em}j\right)}$(4) where B (i,j) represents vessel pixels and S(i,j) represents skeleton pixels.
VPI	Vessel perimeter map (Fig. 4(d)) obtained from vessel map. Ratio of perimeter area and total image area was defined as VPI [23]. $\text{Vessel perimeter index}=\frac{{{\displaystyle \sum }}_{\text{i}=1,\hspace{0.17em}\text{j}=1}^{\text{n}}\text{P}\left(\text{i},\hspace{0.17em}\text{j}\right)}{{{\displaystyle \sum }}_{\text{i}=1,\hspace{0.17em}\text{j}=1}^{\text{n}}\text{I}\left(\text{i},\hspace{0.17em}\text{j}\right)}$(5) where P (i,j) represents perimeter pixels and I(i,j) represents all the pixels in vessel perimeter map.
FAZ Area	FAZ demarcated from OCTA image (Fig. 4(e)) and area calculated using following equation [23], $\text{FAZ}=(\text{Area of single pixel}\left(\text{in}\hspace{0.17em}\mathrm{\mu }{\text{m}}^2\right)\times {\displaystyle \sum }_{\text{i}=1,\hspace{0.17em}\text{j}=1}^{\text{n}}\text{A}\left(\text{i},\hspace{0.17em}\text{j}\right)$(6) where A (i,j) represents the pixels occupied by the segmented avascular region.
FAZ contour irregularity	FAZ contour segmented (Fig. 4(f)) and the irregularity was calculated using following equation [23], $\text{Contour irregularity}=\frac{{{\displaystyle \sum }}_{\text{i}=1,\hspace{0.17em}\text{j}=1}^{\text{n}}\text{O}\left(\text{i},\hspace{0.17em}\text{j}\right)}{{{\displaystyle \sum }}_{\text{i}=1,\hspace{0.17em}\text{j}=1}^{\text{n}}\text{R}\left(\text{i},\hspace{0.17em}\text{j}\right)}$(7) where O (i,j) represents the FAZ contour pixels and R (i,j) represents the pixels occupied by the perimeter of the reference circle.
PAD	Local fractal dimension (LFD) with moving window of size of 3 × 3, 5 × 5, 7 × 7, 9 × 9 and 11 × 11 pixels were calculated using following equation [28], $\text{FD}=\frac{\text{log}({\text{N}}_{\mathrm{s}})}{\text{log}(\text{s})}$(8) where $N_s$ is the number of boxes of magnification s needed to enclose the image. Normalized LFD value close to 1 indicates large vessels while 0 indicates avascular regions [28].

2.4 Classification

We tested three classifiers, i.e., discriminant analysis, KNN, and SVM, to classify the OCTA images and compared their performances. We conducted two types of classification of OCTA images for all three classifiers. First, we implemented the algorithms to identify SCR patients and control subjects. Second, we classified the mild and severe stages of SCR.

For SCR vs. control classification, we used a ‘hold out’ validation technique. The holdout method divides the data into two mutually exclusive subsets, i.e., a training set and a test set. It is standard to designate approximately two-third of the data (60% ~ 70%) as the training set and the remaining data (30% ~ 40%) as the test set [29, 30]. We selected 40% of data randomly (‘hold out’ 40%) for test phase and the rest 60% for training the classifiers. In our previous study, the features showed sensitivity towards SCR patient data, so a basic ‘hold out’ validation was practical and sufficient for classification.

For the mild vs. severe stage classification, there were only 6 SCD patients (12 OCTA images) out of 35 (70 OCTA images) with stage III or higher retinopathy. Therefore, we used a more robust k-fold cross validation technique [29–32]. In this validation technique, the data set is randomly split into k mutually exclusive subsets where the subsets are almost equal size. The classifier is trained and tested k times. The final accuracy is the average of the k iterations. The cross validation limits overfitting and multiple runs of the algorithm using different splits confirm the robustness and repeatability of the classification [29–31]. ‘Leave P out’ is a simple type of cross validation where each learning set is created from M samples by taking all the samples except P (P = 1, 2, 3… M). The test set consists of the P samples left out. This cross-validation procedure does not waste much data as only limited amount of samples are removed from the training set but it is often computationally costly [29–31]. However, as our database was smaller, this was more practical approach and did not affect the computation time significantly. Since we had only 12 OCTA data for severe stage SCR patients, we tested our classifiers using P = 1 to 6. The results were similar, but P = 4 produced the best average performance.

The automated algorithm was implemented in MATLAB hosted in a 4-core desktop computer with a Windows-7 64-bit operating system, Core i7-4770 CPU at 3.4 GHz (Intel, Santa Clara, CA, USA), and 16 GB of RAM. For discriminant analysis, we used the MATLAB function ClassificationDiscriminant.fit. This function employs a quadratic discriminant classifier which is more robust when the two classes of data could have variable covariance. For KNN, we used the ClassificationKNN.fit function with a standardized Euclidean distance metric and set k = 1 as default in Matlab. The 1- nearest neighbor classifier is independent of tuning parameters and has a low risk of overfitting [33]. For SVM we employed a one versus one class decision in an error-correcting output code multiclass (ECOC) model [34, 35]. We used svmtrain and svmclassify functions in Matlab with Gaussian radial basis function (RBF) kernel with sigma = 1. The RBF kernel is accepted as a reliable method for nonlinear data [29, 30]. The average time for processing a single OCTA image and extracting the feature vectors was ~5.2 seconds. The whole classification process for SCR vs. control and mild vs. severe stage took ~2.6 seconds and ~4.7 seconds respectively including the training of the data set with 6 feature vectors and classifying the test set.

The performances of the three classification algorithms were assessed by calculating three comparison metrics, i.e., sensitivity, specificity and accuracy, from the classification matrix. Sensitivity and specificity show the ratio of the cases (control vs. disease or mild vs. severe stage) correctly identified by the classifiers. However, they don’t represent all aspects of the performance. So, accuracy metric was also measured which gives more balanced and comprehensive representation of classification performance. Following equations were used to calculate the sensitivity, specificity and accuracy [36].

$$\text{Sensitivity}=\frac{\mathrm{A}}{\mathrm{A}+\mathrm{C}}$$ (9)

$$\text{Specificity}=\frac{\mathrm{D}}{\mathrm{B}+\mathrm{D}}$$ (10)

$$\text{Accuracy}=\frac{\mathrm{A}+\mathrm{D}}{\mathrm{A}+\mathrm{B}+\mathrm{C}+\mathrm{D}}$$ (11)

where A = True positive, B = True negative, C = False negative, D = False positive.

3. Results

Table 2 demonstrates the performance of the SVM classifier in terms of sensitivity, specificity, and accuracy (the highest percentage possible is 100%) [37]. The six features are conceptually different and they measure different aspects of the OCTA image texture. Therefore, we speculated that the classification performance could be improved by comprehensive involvement of multiple features. Combined feature analysis have been used in colorectal cancer histology [38]. We used each of the single parameters and trained an SVM classifier to identify control and two stages of SCR. The performance of the single feature was then compared to that of combined features. Although features like BVD, FAZ area, contour irregularity and PAD show acceptable classification accuracy (~90%), increased accuracy was observed by compiling all these six quantitative features. The comprehensive features demonstrate 100% accuracy for SCR vs. control and 97% accuracy for mild vs. severe classification. We also observe 100% sensitivity and 100% specificity for SCR vs. control classification which indicates that the SVM classifier could identify SCR and control samples in 100% cases. For mild vs. severe stages the percentages were 97% and 95%, respectively. We performed a Pearson’s correlation analysis of the six features and found low correlation between the feature subsets. This supports that different features reflect different aspects of the OCTA images and combined features could be more reliable for SCR classification.

Table 2. Performance comparison between single and combined features.

Parameters	Sensitivity (%)		Specificity (%)		Accuracy (%)
	SCR vs. control	Mild vs. Severe	SCR vs. control	Mild vs. Severe	SCR vs. control	Mild vs. Severe
BVT	91	93	85	90	87	93
BVD	87	93	80	87	82	92
VPI	81	80	78	78	80	80
FAZ area	94	91	92	89	94	91
FAZ contour irregularity	91	90	86	88	89	90
PAD	92	90	89	87	91	89
All 6 parameters	100	97	100	95	100	97

We also incorporated the combined features to train two other classification algorithms, KNN and discriminant analysis. The detailed comparison of classification performance can be seen in Table 3. For SCR vs. control, all three classifiers perform well with an average accuracy of 95% using the quantitative features. For mild SCR vs. severe SCR classification, SVM shows better performance compared to the other two classifiers. Among all 3 classifiers, SVM shows the best performance with 100% sensitivity, 100% specificity and 100% accuracy for SCR vs. control classification and 97% sensitivity, 98% specificity and 97% accuracy for mild vs. severe stage classification.

Table 3. Performance analysis of three classifiers (using all 6 parameters).

Classifiers	Sensitivity (%)		Specificity (%)		Accuracy (%)
	SCR vs. control	Mild vs. Severe	SCR vs. control	Mild vs. Severe	SCR vs. control	Mild vs. Severe
Support vector machine	100	97	100	95	100	97
K-nearest neighbor	95	96	93	92	93	95
Discriminant analysis	93	88	92	86	92	88

4. Discussion

In the study, we have demonstrated automated algorithms for computer-aided SCR classification with six OCTA features, including BVT, BVD, VPI, FAZ area, FAZ contour irregularity, PAD. All of the classification algorithms (discriminant analysis, KNN and SVM) showed good performance with decent sensitivity and specificity for SCR vs. control and had an average accuracy of 95%. However, SVM showed superior results with 100% accuracy in detecting SCR patients from optimized feature vectors. For mild vs. severe stage classification, SVM shows better performance than discriminant analysis and KNN algorithm. A relatively lower specificity values for the discriminant analysis and KNN algorithm than SVM may be due to the smaller population of severe stage SCR patients in the database. However, SVM still shows a 97% accuracy detecting mild vs. severe SCR patients. The automated algorithm establishes the feasibility of the OCTA parameters as quantitative features.

For both types of classification, we quantitatively compared the performance of three classifiers. Discriminant analysis and KNN are two most common and basic machine learning algorithms [30, 31, 38, 39]. We wanted to compare these basic algorithms to SVM which is known to be robust for small data set, and has been a widely used algorithm in other research fields [31, 39]. The limitation of discriminant analysis is that it assumes the population to have normality (probability distribution function is normally distributed) and same covariance. Therefore, it is challenging to classify nonlinear and low amount of data points using this algorithm. For this reason, it did not perform so well in mild vs. severe classification. In case of control vs. SCR, the features did not exactly have normality but had smaller standard deviation. So discriminant analysis performed moderately. In case of KNN, a major challenge is tuning the value of K and the distance metric for classification. KNN algorithm is highly sensitive to this optimization. KNN is also very sensitive to outliers and less intuitive with low data points. In mild vs. severe classification, with lower data points, even a few outliers in feature vectors resulted in lower performance of KNN. In contrary, SVM works well even in case of nonlinear data points and small image data sets as it demonstrates less model assumption, less outlier sensitivity and less nearby point dependency [31, 34, 38, 40]. Along with our cross validation technique SVM limits the tendency of overfitting data more effectively compared to KNN and discriminant analysis [34, 40]. We used a radius basis function (RBF) kernel which is very practical in this kind of cases. Thus we observed the best classification performance by SVM in both control vs. SCR and mild vs. severe classification. Our ‘hold 4 out’ validation technique to choose training and test sets from SCR data in each iteration is also practical for small data sets and ensures robust and repeatable classification performance.

For performance comparison, we used each of the quantitative features for classification of control and SCR stages. We can observe that BVT, FAZ area, contour irregularity and PAD shows decent performance as features to train an SVM classifier. In our previous study, these features also showed the most sensitivity to SCR. So as feature vectors, they were also successful to classify among control, mild and severe SCR stages (about 90% sensitivity and accuracy). However, considering the robustness and reliability of computer-aided classification, using all of the quantitative features to train and test the classifiers demonstrated better results as can be seen in Table 2. It’s observed that classification sensitivity, specificity, and accuracy are improved due to the comprehensive involvements of multiple OCTA features.

For computer-aided diagnosis applications, an essential aspect of the process is the computation time. Especially in classification applications, the time needed for feature extraction, training and testing the algorithms often creates a challenge for practical implementation. Our automated algorithm shows significant fast processing time which can make it a valuable tool for computer-aided diagnosis. For a single OCTA image, it takes only an average of 5.2 seconds to extract all the six features. It takes 2.6 seconds for SCR vs. control and 4.7 for mild vs. severe stage classification. These time parameters include the time required to train and test the classifiers. The fast computation time of the algorithm will provide clinicians an effective and efficient diagnostic tool.

5. Conclusion

In conclusion, we demonstrate computer-aided SCR classification using six quantitative OCTA parameters. This method can automatically differentiate and classify SCR vs control and mild vs severe SCR eyes. Three classification algorithms were quantitatively compared by calculating sensitivity, specificity and accuracy metrics. It was also observed that combined features show improved classification performance, compared to single feature. SVM performs the best to classify SCR patients and their stages. This study establishes the feasibility of using quantitative OCTA biomarkers as feature vectors to achieve objective and automated SCR classification. We anticipate that, in coordination with affordable internet technology, the computer-aided SCR classification promises telemedicine screening to improve access to eye care for patients in rural and underserved areas.

Disclosures

The authors declare that there are no conflicts of interest related to this article.

Funding

NIH grants R01 EY023522, R01 EY024628, P30 EY001792; by unrestricted grant from Research to Prevent Blindness; by Richard and Loan Hill endowment; by Marion H. Schenck Chair endowment.