Dynamic approach to predict pH profiles of biologically relevant buffers

Abstract

Recently, dynamic approach has been applied to determine the steady state concentrations of multiple ionic species present in complex buffers at equilibrium. Here, we have used the dynamic approach to explicitly model the pH profiles of biologically relevant phosphate buffer and universal buffer (a mixture of three tri-protic acids such as citric acid, boric acid and phosphoric acid). The results from dynamic approach are identical to that of the conventional algebraic approach, but with an added advantage that the dynamic approach, allow for the modelling of complex buffer systems relatively easy compared to that of algebraic method.

Graphical abstract

Highlights

• •Accurate model proposed for Phosphate and Universal buffer using dynamic approach.
• •Optimization of pKa values in phosphate and universal buffer using dynamic approach.
• •A method that than be easily extended to predict pH of complex bio-fluids if concentration of metabolites and its pKa values are known.

1. Introduction

Buffer preparation is an integral part of several in-vitro and in-vivo experiments performed in biological studies. Buffer by definition is a mixture of weak acid and its conjugate base, or a mixture of weak base and its conjugate acid. The pK_a of the weak acid or the pK_b of the weak base defines the buffering capacity of the buffers used for in the experiments. Simple buffers are prepared by titrating specified quantity of acid/base (mono-, di- or tri- acidic/alkaline) against alkali/acid till the desired pH is achieved. It is necessary that the final pH should be within the buffering capacity of the acid/base being considered, for the buffer to be effective. Biologically relevant buffers such as phosphate buffers are prepared by titrating equi-molar concentration of mono hydrogen phosphate against dihydrogen phosphate or vice-versa till a desired pH is reached. Complex buffer such as universal buffer are prepared by titrating a mixture of two or three tri-protic acids with an alkali or tri-sodium salt of phosphoric acid [1].

Two mathematical approaches namely, the algebraic [2], [3] and the dynamic approach [4], [5], [6] are available to predict the pH profiles of complex buffer systems. In this work, we explicitly derive the analytical expression for phosphate and universal buffer using algebraic as well as differential dynamic approach. The derived models were used to back-predict the pH profiles of phosphate and universal buffer solutions reported earlier [7]. The theoretical predictions are in good agreement with the experimental data, validating the accuracy of the proposed models.

2. Theory

Consider the volumetric titration of a weak mono-protic acid ($\mathit{HA}$) in the presence of strong alkali such as $\mathit{NaOH}$. At the outset, the weak acid exists in the form of both unionized form $[\mathit{HA}]$ and its ionized form $[A^{-}]$. The equilibrium between these two states can be written as (Eq. (1)),

$$\mathit{HA}\begin{array}{c}{k}_1\\ \iff \\ k_{-1}\end{array}{H}^{+}+A^{-}$$ (1)

$k_1$, $k_{-1}$ are the kinetic rates for the dissociation and association of the weak acid, respectively. The irreversible dissociation of alkali during the titration is given by (Eq. (2)),

$$\mathit{NaOH}\stackrel{k_2}{\to }{\mathit{Na}}^{+}+{\mathit{OH}}^{-}$$ (2)

$k_2$ is the kinetic rate for the irreversible dissociation of the alkali. Unlike, weak acid, the dissociation of the strong base/acid are represented through irreversible reactions. Finally the dissociation of water is given by (Eq. (3)),

$$H_{2}O\begin{array}{c}{k}_w\\ \iff \\ k_{-w}\end{array}{H}^{+}+{\mathit{OH}}^{-}$$ (3)

$k_w$,$k_{-w}$ are the forward and reverse kinetic rates for the dissociation of water, respectively. The pH profile of the weak acid upon addition of alkali results in a typical weak acid-base titration curve containing buffering region (where, pH=pK_a) and equivalence point [8], [2], [3]. To predict the pH profile of a titration, an analytical equation that relates pH with the concentration of the alkali is necessary [9]. The derivation for such titrations are available in several literatures, text-books and online resources [10] (please refer supporting information). The first step in the derivation involves, expression of the mole fractions of [HA] and [A^-] in terms of total acid [A_T] and the equilibrium constant K₁, using law of mass balance equation [HA]+[A^-]=[A_T]. The second step involves, assumption of charge neutrality of the solution, i.e, [H⁺]+[Na⁺] =[OH^-]+[A^-]. Re-expression of all variables in the charge balance equation, in terms of [H⁺] would result in a polynomial equation. Based on the order of the polynomial equation, multiple roots are available. Choosing the correct root value that is physically relevant would yield the [H⁺] ion concentration. The negative logarithm to the base 10 of [H⁺] is defined as the pH value (pH=-log₁₀ [H⁺]). By varying [Na⁺], the titrated alkali concentration, different polynomials are obtained. Each polynomial equation is solved separately to determining the pH profile of the titration curve.

Alternatively, pH can also be predicted using dynamic approach, where we first assume a kinetic model and then frame a set of differential equation based on the model [6] (please refer Supporting information).

$$\frac{d\left[\mathit{HA}\right]}{\mathit{dt}}=-k_1\left[\mathit{HA}\right]+k_{-1}\left[A^{-}\right]\left[H^{+}\right]$$ (4)

$$\frac{d\left[A^{-}\right]}{\mathit{dt}}=+k_1\left[\mathit{HA}\right]-k_{-1}\left[A^{-}\right]\left[H^{+}\right]$$ (5)

$$\frac{d\left[H^{+}\right]}{\mathit{dt}}=+k_1\left[\mathit{HA}\right]-k_{-1}\left[A^{-}\right]\left[H^{+}\right]+k_w-k_{-w}\left[H^{+}\right]\left[{\mathit{OH}}^{-}\right]$$ (6)

$$\frac{d\left[{\mathit{OH}}^{-}\right]}{\mathit{dt}}=+k_w-k_{-w}\left[H^{+}\right]\left[{\mathit{OH}}^{-}\right]$$ (7)

In the above differential equations from (4), (5), (6), (7); [HA] and [A^-] are the unionized and the ionized species of the weak acid, respectively. [H⁺] is the proton generated by dissociation of acid as well as water. [OH^-] is the hydroxyl ion generated from dissociation of alkali as well as water. [NaOH] is the alkali component (sodium hydroxide) used in the titration. Since, [NaOH] dissociates completely to [Na⁺] and [OH^-], immediately after it's addition to the solution, the dissociated [OH^-] arising from [NaOH] can be directly added to the initial concentration of [OH^-], present at the onset of the titration. Thereby, the rate equation for [NaOH] can be explicitly excluded from the above model.

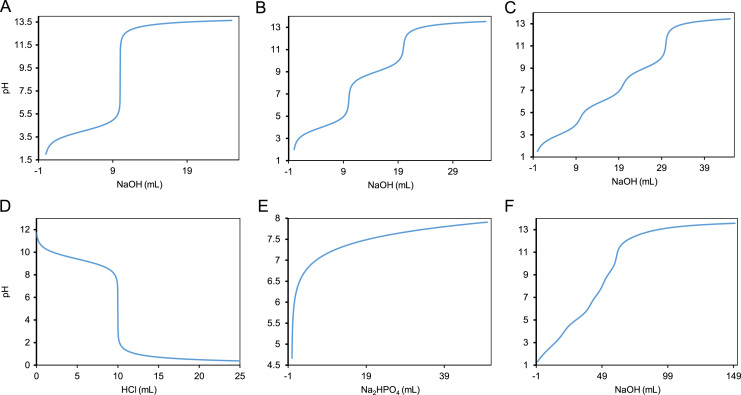
In order to obtain a steady-state concentration, the above set of coupled differential equations are integration over a long period of time, such that, the equilibrium state had been reached. The [H⁺] concentration obtained after equilibrium is achieved can be used to calculate the pH profile of the titration. The simulations of mono-protic, di-protic, tri-protic, phosphate buffer and universal buffer titrated with NaOH is shown in Fig. 1. Additionally, the titration of amino-hydroxyl compound with HCl is also presented in Fig. 1. The simulations carried out using algebraic as well as dynamic approach generated identical results. For the simulation of mono-protic acid, the rate constants $k_1$, $k_{-1}$,$k_w$, $k_{-w}$, were set to 10⁻⁴, 1.0, 10^–14, 1.0 s⁻¹, respectively. The matlab [11] codes for simulation of mono-protic acid is provided in the supporting information. The simulation of di-protic acid was carried out using rate constants, $k_1$, $k_{-1}$, $k_2$, $k_{-2}$,$k_w$, $k_{-w}$, whose values set to 10⁻⁴, 1.0, 10⁻⁹, 1.0, 10^–14,1.0 s⁻¹, respectively. The $k_2$, $k_{-2}$ are the $k_{\mathit{on}}$, $k_{\mathit{off}}$ rate constants for the second ionisable moiety of the di-protic acid. The simulation of tri-protic acid was carried out using rate constants, $k_1$, $k_{-1}$, $k_2$, $k_{-2}$, $k_3$, $k_{-3}$,$k_w$, $k_{-w}$, whose values set to 10⁻³, 1.0, 10⁻⁶, 1.0, 10⁻⁹, 1.0, 10^–14,1.0 s⁻¹, respectively. The $k_3$, $k_{-3}$ are the $k_{\mathit{on}}$, $k_{\mathit{off}}$ rate constants for the third ionisable moiety of the tri-protic acid. The simulation of mono-hydroxyl alkali was carried out using rate constants, $k_{b1}$, $k_{-b1}$,$k_w$, $k_{-w}$, whose values set to 10^−9.24, 1.0, 10^–14,1.0 s⁻¹, respectively. The $k_{b1}$, $k_{-b1}$ are the $k_{\mathit{on}}$, $k_{\mathit{off}}$ rate constants for the dissociation of alkali component. The matlab codes for simulation of mono-alkaline species is provided in the supporting information.

Fig. 1.

The simulation of pH profile obtained for titration of mono-protic (A), di-protic (B), tri-protic (C), mono-alkaline (D), Phosphate buffer (E), Universal buffer (F). NaOH was considered as a titrant for (A), (B), (C), (F). HCl was considered as titrant for (D). Na₂HPO₄ was considered as titrant for (E). For simulation, pKa was set to 4 for mono-protic acid, 4,9 for di-protic acid, 3,6,9 for tri-protic acid, 4.6 or pK_b=9.245 for mono-alkaline, 2.12,7.21,12.32 for phosphate buffer. For universal buffer the pKa values were set to 2.12, 7.21, 12.32 for phosphoric acid, 3.08, 4.72, 5.4 for citric acid, 9.23, 12.4, 13.3 for Boric acid. The simulation of phosphate buffer assumes titration of NaH₂PO₄ with incremental volume of Na₂HPO₄. Both the algebraic and dynamic approach yielded identical profiles for all the simulations.

2.1. Phosphate buffer

2.1.1. Kinetic model for phosphate buffer

Phosphoric acid is a tri-protic acid with three pK_a values. Preparation of phosphate buffer involves titration of equi-molar concentration of mono hydrogen phosphate into di-hydrogen phosphate or vice versa. We assume the following kinetic model to predict the pH profile of the phosphate buffer,

$$H_3{\mathit{PO}}_4\begin{array}{c}{k}_1\\ \iff \\ k_{-1}\end{array}{H}^{+}+{H_2{\mathit{PO}}_4}^{-}$$ (8)

$${H_2{\mathit{PO}}_4}^{-}\begin{array}{c}{k}_2\\ \iff \\ k_{-2}\end{array}{H}^{+}+{H{\mathit{PO}}_4}^{2-}$$ (9)

$${H{\mathit{PO}}_4}^{2-}\begin{array}{c}{k}_3\\ \iff \\ k_{-3}\end{array}{H}^{+}+{{\mathit{PO}}_4}^{3-}$$ (10)

In the above Eqs., (8), (9), (10), [H₂PO₄^-], [HPO₄^2-], [PO₄^3-], represent the mono-, di-, trivalent phosphate species generated by dissociation of the phosphoric acid [H₃PO₄].

$$\mathit{Na}{H}_2{\mathit{PO}}_4\stackrel{k_4}{\to }{\mathit{Na}}^{+}+{H_2{\mathit{PO}}_4}^{-}$$ (11)

$${\mathit{Na}}_{2}H{\mathit{PO}}_4\stackrel{k_5}{\to }{2\mathit{Na}}^{+}+{H{\mathit{PO}}_4}^{2-}$$ (12)

$$H_{2}O\begin{array}{c}{k}_w\\ \iff \\ k_{-w}\end{array}{H}^{+}+{\mathit{OH}}^{-}$$ (13)

In the above Eqs. (11), (12), (13), $[\mathit{Na}{H}_2{\mathit{PO}}_4]$ is the acid component added in the form of mono-sodium salt of phosphoric acid. $[{\mathit{Na}}_{2}H{\mathit{PO}}_4]$ is the alkali component added in the form of di-sodium salt of phosphoric acid. [H⁺] is the proton generated during the dissociation of acid as well as water; and [OH^-] is the hydroxyl ion generated by dissociation of alkali as well as water. $k_1$, $k_2$, $k_3$, $k_w$ are the forward kinetic rates and $k_{-1}$, $k_{-2}$, $k_{-3}$, $k_{-w}$ are the reverse kinetic rates for the equilibriums in Eqs. (8), (9), (10), (13), respectively. $k_4$, $k_5$, in Eqs. (11), (12) are the irreversible dissociation rates of $[\mathit{Na}{H}_2{\mathit{PO}}_4]$, $[{\mathit{Na}}_{2}H{\mathit{PO}}_4]$, respectively. The simulation of phosphate buffer was carried out using rate constants, $k_1$, $k_{-1}$,$k_2$, $k_{-2}$, $k_3$, $k_{-3}$,$k_w$, $k_{-w}$, whose values set to 10^−2.12, 1.0, 10^−7.21, 1.0, 10^–12.32, 1.0, 10^–14,1.0 s⁻¹, respectively. The irreversible dissociation rates of both mono and di-sodium phosphate salts, $k_4$, $k_5$ were set to 10² s⁻¹ (Fig. 1).

2.1.1.1. Algebraic method for phosphate buffer

The charge neutrality equation for such a system can be written as (Eq. (14)),

$$\left[H^{+}\right]+2{\left[N{a}_{2}HP{O}_4\right]}_0+{\left[Na{H}_{2}P{O}_4\right]}_0=\left[O{H}^{-}\right]+\left[H_{2}P{O}_{4^{-}}\right]+2\left[HP{O}_4^{2-}\right]+3\left[P{O}_4^{3-}\right].$$ (14)

Since, ${[\mathit{Na}{H}_2{\mathit{PO}}_4]}_0$ and ${[{\mathit{Na}}_{2}H{\mathit{PO}}_4]}_0$, the mono-, di-sodium salt of phosphate, dissociate completely, its concentration can be directly substituted in to the above equation. Further, ${[\mathit{Na}{H}_2{\mathit{PO}}_4]}_0$ and ${[{\mathit{Na}}_{2}H{\mathit{PO}}_4]}_0$, represent the acidic and alkali components of the titration. By re-expressing all the other components such as [ OH^-], [H₂PO₄^-], [HPO₄^2-], [PO₄^3-], in terms of [H⁺], the above equation simplifies to a polynomial of order 5 in [H⁺] (Eq. (15)).

$${H^5+\left(B_T+K_1\right)H}^4+\left(B_T*K_1-A_T*K_1-K_W+K_1*K_2\right)*H^3+{(B}_T*K_1*K_2-{2A}_T*K_1*K_2-K_1*K_W+K_1*K_2*K_3)*H^2+{(B}_T*K_1*K_2*K_3-3*A_T*K_1*K_2*K_3-K_1*K_2*K_W)*H-K_1*K_2*K_3*K_W=0$$ (15)

$K_1$, $K_2$, $K_3$ and $K_W$ are the equilibrium constants obtained from the equilibrium conditions, represented by Eqs., (8), (9), (10), (13), respectively. The ratio of forward kinetic rate to reverse kinetic rate yields the equilibrium constants; i.e., $K_1=\frac{k_1}{k_{-1}}$ ,$K_2=\frac{k_2}{k_{-2}}$, $K_3=\frac{k_3}{k_{-3}}$. By solving the polynomial, Eq. (15), for a given $A_T$ and $B_T$, the concentration of ${[\mathit{Na}{H}_2{\mathit{PO}}_4]}_0$ and ${[{\mathit{Na}}_{2}H{\mathit{PO}}_4]}_0$, and selecting a physically relevant root, the pH can be determined. By varying A_T and B_T, in Eq. (15), the pH profile of a complete titration can be obtained. (Matlab code to symbolically derive Eq. (15) is available in the supporting information).

2.1.1.2. Dynamic approach for phosphate buffer

To predict the pH for a titration curve using differential approach, we frame the following system of differential equations based on the kinetic model (Eqs. (8), (9), (10), (11), (12), (13)),

$$\frac{d\left[H_3{\mathit{PO}}_4\right]}{\mathit{dt}}=-k_1\left[H_3{\mathit{PO}}_4\right]+k_{-1}\left[{H_2{\mathit{PO}}_4}^{-}\right]\left[H^{+}\right]$$ (16)

$$\frac{d\left[{H_2{\mathit{PO}}_4}^{-}\right]}{\mathit{dt}}=+k_1\left[H_3{\mathit{PO}}_4\right]-k_{-1}\left[{H_2{\mathit{PO}}_4}^{-}\right]\left[H^{+}\right]-k_2\left[{H_2{\mathit{PO}}_4}^{-}\right]+k_{-2}\left[{H{\mathit{PO}}_4}^{2-}\right]\left[H^{+}\right]$$ (17)

$$\frac{d\left[{H{\mathit{PO}}_4}^{2-}\right]}{\mathit{dt}}=k_2\left[{H_2{\mathit{PO}}_4}^{-}\right]-k_{-2}\left[{H{\mathit{PO}}_4}^{2-}\right]\left[H^{+}\right]-k_3\left[{H{\mathit{PO}}_4}^{2-}\right]+k_{-3}\left[{{\mathit{PO}}_4}^{3-}\right]\left[H^{+}\right]$$ (18)

$$\frac{d\left[{{\mathit{PO}}_4}^{3-}\right]}{\mathit{dt}}=+k_3\left[{H{\mathit{PO}}_4}^{2-}\right]-k_{-3}\left[{{\mathit{PO}}_4}^{3-}\right]\left[H^{+}\right]$$ (19)

$$\frac{d\left[H^{+}\right]}{\mathit{dt}}=+k_1\left[H_3{\mathit{PO}}_4\right]-k_{-1}\left[{H_2{\mathit{PO}}_4}^{-}\right]\left[H^{+}\right]+k_2\left[{H_2{\mathit{PO}}_4}^{-}\right]-k_{-2}\left[{H{\mathit{PO}}_4}^{2-}\right]\left[H^{+}\right]+k_3\left[{H{\mathit{PO}}_4}^{2-}\right]-k_{-3}\left[{{\mathit{PO}}_4}^{3-}\right]\left[H^{+}\right]+k_w-k_{-w}\left[H^{+}\right]\left[{\mathit{OH}}^{-}\right]$$ (20)

$$\frac{d\left[{\mathit{OH}}^{-}\right]}{\mathit{dt}}=+k_w-k_{-w}\left[H^{+}\right]\left[{\mathit{OH}}^{-}\right]$$ (21)

The contribution of the dissociation of mono-sodium salt, [NaH₂PO₄]₀ and di-sodium salt, [Na₂HPO₄]₀ are added directly to the initial concentrations of [H₂PO₄^-] and [HPO₄^2-], respectively. The above set of coupled differential equations (Eqs.(16), (17), (18), (19), (20), (21)) can be numerically integrated for a given initial condition/concentration set at 0, [NaH₂PO₄]₀, [Na₂HPO₄]₀, 0, 10⁻⁷, 10⁻⁷, respectively. [NaH₂PO₄]₀, [Na₂HPO₄]₀, are the initial concentrations of mono-sodium phosphate and di-sodium phosphate salts, respectively, which constitutes the acidic and alkali components present in the mixture. The concentrations of [NaH₂PO₄]₀ and [Na₂HPO₄]₀, were varied for each simulation to obtain the entire pH profile of the titration data. The simulation of phosphate buffer using algebraic and dynamic approach is shown in Fig. 1(E).

2.2. Universal buffer

2.2.1. Kinetic model for universal buffer

Universal buffer contains a mixture of three tri-protic acids namely, phosphoric acid, citric acid and boric acid. The preparation of universal buffer involves, preparing a mixture of citric and boric acid at appropriate concentrations and titrating it against tri-sodium salt of phosphoric acid to a desired pH value.

We assumed the following kinetic model for the universal buffer:

$$H_3{\mathit{PO}}_4\begin{array}{c}{k}_1\\ \iff \\ k_{-1}\end{array}{H}^{+}+{H_2{\mathit{PO}}_4}^{-}$$ (22)

$${H_2{\mathit{PO}}_4}^{-}\begin{array}{c}{k}_2\\ \iff \\ k_{-2}\end{array}{H}^{+}+{H{\mathit{PO}}_4}^{2-}$$ (23)

$${H{\mathit{PO}}_4}^{2-}\begin{array}{c}{k}_3\\ \iff \\ k_{-3}\end{array}{H}^{+}+{{\mathit{PO}}_4}^{3-}$$ (24)

$${\mathit{Na}}_3{\mathit{PO}}_4\stackrel{k_4}{\to }{\mathit{Na}}^{3+}+{{\mathit{PO}}_4}^{3-}$$ (25)

$$H_{3}C\begin{array}{c}{k}_5\\ \iff \\ k_{-5}\end{array}{H}^{+}+{H_{2}C}^{-}$$ (26)

$${H_{2}C}^{-}\begin{array}{c}{k}_6\\ \iff \\ k_{-6}\end{array}{H}^{+}+{\mathit{HC}}^{2-}$$ (27)

$${\mathit{HC}}^{2-}\begin{array}{c}{k}_7\\ \iff \\ k_{-7}\end{array}{H}^{+}+C^{3-}$$ (28)

$$H_{3}B\begin{array}{c}{k}_8\\ \iff \\ k_{-8}\end{array}{H}^{+}+{H_{2}B}^{-}$$ (29)

$${H_{2}B}^{-}\begin{array}{c}{k}_9\\ \iff \\ k_{-9}\end{array}{H}^{+}+{\mathit{HB}}^{2-}$$ (30)

$${\mathit{HB}}^{2-}\begin{array}{c}{k}_{10}\\ \iff \\ k_{-10}\end{array}{H}^{+}+B^{3-}$$ (31)

$$H_{2}O\begin{array}{c}{k}_w\\ \iff \\ k_{-w}\end{array}{H}^{+}+{\mathit{OH}}^{-}$$ (32)

In the above Eqs. (22), (23), (24), (25), (26), (27), (28), (29), (30), (31), (32), [H₂PO₄^-], [HPO₄^2-], [PO₄^3-], are the mono-, di-, tri-, anionic species generated from phosphoric acid [H₃PO₄], respectively. Na₃PO₄ is the alkali component added in the form of tri-sodium salt of phosphoric acid. [H₂C^-], [HC^2-], [C^3-], are the mono-, di- and tri-, anionic species generated from citric acid [H₃C], respectively. [H₂B^-], [HB^2-], [B^3-], are the mono-, di- and tri-, anionic species generated from boric acid [H₃B], respectively. [H⁺], is the proton generated by dissociation of acids as well as water and [OH^-], is the hydroxyl ion generated by dissociation of alkali as well as water. Except for Eq. (25), which is irreversible and leads to complete dissociation of [Na₃PO₄]₀ with rate constant, $k_4$, in solution, all the other reactions are reversible by nature. $k_1$, $k_2$, $k_3$, $k_5$, $k_6$, $k_7$, $k_8$, $k_9$, $k_{10}$,$k_w$, are the forward kinetic rates and $k_{-1}$, $k_{-2}$, $k_{-3}$, $k_{-5}$, $k_{-6}$, $k_{-7}$, $k_{-8}$, $k_{-9}$, $k_{-10}$,$k_{-w}$, are the reverse kinetic rates for the equilibriums in Eqs. (25), (27), (28), (30)–(33), (35), (36), respectively. The simulation of universal buffer was carried out using rate constants, $k_1$, $k_{-1}$, $k_2$, $k_{-2}$, $k_3$, $k_{-3}$, $k_4$, $k_5$, $k_{-5}$, $k_6$, $k_{-6}$, $k_7$, $k_{-7}$, $k_8$, $k_{-8}$, $k_9$, $k_{-9}$,$k_{10}$, $k_{-10}$, $k_w$, $k_{-w}$, whose values set to 10^−2.12, 1.0, 10^−7.21, 1.0, 10^–12.32, 1.0, 10² ,10^−3.08, 1.0, 10^−4.74, 1.0, 10^−5.4, 1.0, 10^−9.23, 1.0, 10^–12.4, 1.0, 10^–13.3, 1.0, 10^–14, 1.0 s⁻¹, respectively. The rate constants $k_1$ through $k_{-3}$, corresponds to kinetic dissociation of phosphoric acid, $k_5$ through $k_{-7}$, corresponds to kinetic dissociation of citric acid, $k_8$ through $k_{-10}$, corresponds to kinetic dissociation of boric acid. The rate constant, $k_4$, represents the irreversible dissociation of tri-sodium phosphate, which was considered to be the sole alkali component of the titration (Fig. 1).

Alternatively, universal buffer can also be prepared by titrating a mixture of phosphoric, citric and boric acid with NaOH. The kinetic model for such a system will differ by inclusion of dissociation of [NaOH]₀ instead of [Na₃PO₄]₀. The simulation of universal buffer system with NaOH as alkali titrant is shown in Fig. 1(F). In the present work, we will be considering universal buffer which is prepared by titrating mixture of citric and boric acid with Na₃PO₄, as the sole alkali component.

2.2.1.1. Algebraic model used for universal buffer

The charge neutrality equation for the above kinetic model is given by Eq. (33),

$$\left[H^{+}\right]+3\left[N{a}_{3}P{O}_4\right]=\left[O{H}^{-}\right]+\left[H_{2}P{O}_4^{-}\right]+2\left[HP{O}_4^{2-}\right]+3\left[P{O}_4^{3-}\right]+\left[H_2{C}^{-}\right]+2\left[H{C}^{2-}\right]+3\left[C^{3-}\right]+\left[H_2{B}^{-}\right]+2\left[H{B}^{2-}\right]+3\left[B^{3-}\right]$$ (33)

By re-expressing all the components such as [OH^-], [H₂PO₄^-], [HPO₄^2-], [PO₄^3-], [H₂C^-], [HC^2-], [C^3-], [H₂B^-], [HB^2-], [B^3-] in terms of [H⁺] the above equation simplifies to a polynomial equation of order 11 expressed in [H⁺]. The explicit derivation using matlab symbolic functions is available in the supporting information. By solving the polynomial equation and selecting the physically relevant root, the pH can be determined.

2.2.1.2. Dynamic approach for universal buffer

Dynamic approach requires the following set of differential equations based on the above kinetic model,

$$\frac{d\left[H_3{\mathit{PO}}_4\right]}{\mathit{dt}}=-k_1\left[H_3{\mathit{PO}}_4\right]+k_{-1}\left[{H_2{\mathit{PO}}_4}^{-}\right]\left[H^{+}\right]$$ (34)

$$\frac{d\left[{H_2{\mathit{PO}}_4}^{-}\right]}{\mathit{dt}}=+k_1\left[H_3{\mathit{PO}}_4\right]-k_{-1}\left[{H_2{\mathit{PO}}_4}^{-}\right]\left[H^{+}\right]-k_2\left[{H_2{\mathit{PO}}_4}^{-}\right]+k_{-2}\left[{H{\mathit{PO}}_4}^{2-}\right]\left[H^{+}\right]$$ (35)

$$\frac{d\left[{H{\mathit{PO}}_4}^{2-}\right]}{\mathit{dt}}=k_2\left[{H_2{\mathit{PO}}_4}^{-}\right]-k_{-2}\left[{H{\mathit{PO}}_4}^{2-}\right]\left[H^{+}\right]-k_3\left[{H{\mathit{PO}}_4}^{2-}\right]+k_{-3}\left[{{\mathit{PO}}_4}^{3-}\right]\left[H^{+}\right]$$ (36)

$$\frac{d\left[{{\mathit{PO}}_4}^{3-}\right]}{\mathit{dt}}=+k_3\left[{H{\mathit{PO}}_4}^{2-}\right]-k_{-3}\left[{{\mathit{PO}}_4}^{3-}\right]\left[H^{+}\right]$$ (37)

$$\frac{d\left[H_{3}C\right]}{\mathit{dt}}=-k_5\left[H_{3}C\right]+k_{-5}\left[{H_{2}C}^{-}\right]\left[H^{+}\right]$$ (38)

$$\frac{d\left[{H_{2}C}^{-}\right]}{\mathit{dt}}=+k_5\left[H_{3}C\right]-k_{-5}\left[{H_{2}C}^{-}\right]\left[H^{+}\right]-k_6\left[{H_{2}C}^{-}\right]+k_{-6}\left[{\mathit{HC}}^{2-}\right]\left[H^{+}\right]$$ (39)

$$\frac{d\left[{\mathit{HC}}^{2-}\right]}{\mathit{dt}}=k_6\left[{H_{2}C}^{-}\right]-k_{-6}\left[{\mathit{HC}}^{2-}\right]\left[H^{+}\right]-k_7\left[{\mathit{HC}}^{2-}\right]+k_{-7}\left[C^{3-}\right]\left[H^{+}\right]$$ (40)

$$\frac{d\left[C^{3-}\right]}{\mathit{dt}}=+k_7\left[{\mathit{HC}}^{2-}\right]-k_{-7}\left[C^{3-}\right]\left[H^{+}\right]$$ (41)

$$\frac{d\left[H_{3}B\right]}{\mathit{dt}}=-k_8\left[H_{3}B\right]+k_{-8}\left[{H_{2}B}^{-}\right]\left[H^{+}\right]$$ (42)

$$\frac{d\left[{H_{2}B}^{-}\right]}{\mathit{dt}}=+k_8\left[H_{3}B\right]-k_{-8}\left[{H_{2}B}^{-}\right]\left[H^{+}\right]-k_9\left[{H_{2}B}^{-}\right]+k_{-9}\left[{\mathit{HB}}^{2-}\right]\left[H^{+}\right]$$ (43)

$$\frac{d\left[{\mathit{HB}}^{2-}\right]}{\mathit{dt}}=+k_9\left[{H_{2}B}^{-}\right]-k_{-9}\left[{\mathit{HB}}^{2-}\right]\left[H^{+}\right]-k_{10}\left[{\mathit{HB}}^{2-}\right]+k_{-10}\left[B^{3-}\right]\left[H^{+}\right]$$ (44)

$$\frac{d\left[B^{3-}\right]}{\mathit{dt}}=+k_{10}\left[{\mathit{HB}}^{2-}\right]-k_{-10}\left[B^{3-}\right]\left[H^{+}\right]$$ (45)

$$\frac{d\left[H^{+}\right]}{\mathit{dt}}=+k_1\left[H_3{\mathit{PO}}_4\right]-k_{-1}\left[{H_2{\mathit{PO}}_4}^{-}\right]\left[H^{+}\right]+k_2\left[{H_2{\mathit{PO}}_4}^{-}\right]-k_{-2}\left[{H{\mathit{PO}}_4}^{2-}\right]\left[H^{+}\right]+k_3\left[{H{\mathit{PO}}_4}^{2-}\right]-k_{-3}\left[{{\mathit{PO}}_4}^{3-}\right]\left[H^{+}\right]+k_5\left[H_{3}C\right]-k_{-5}\left[{H_{2}C}^{-}\right]\left[H^{+}\right]+k_6\left[{H_{2}C}^{-}\right]-k_{-6}\left[{\mathit{HC}}^{2-}\right]\left[H^{+}\right]+k_7\left[{\mathit{HC}}^{2-}\right]-k_{-7}\left[C^{3-}\right]\left[H^{+}\right]+k_8\left[H_{3}B\right]-k_{-8}\left[{H_{2}B}^{-}\right]\left[H^{+}\right]+k_9\left[{H_{2}B}^{-}\right]-k_{-9}\left[{\mathit{HB}}^{2-}\right]\left[H^{+}\right]+k_{10}\left[{\mathit{HB}}^{2-}\right]-k_{-10}\left[B^{3-}\right]\left[H^{+}\right]+k_w-k_{-w}\left[H^{+}\right]\left[{\mathit{OH}}^{-}\right]$$ (46)

$$\frac{d\left[{\mathit{OH}}^{-}\right]}{\mathit{dt}}=+k_w-k_{-w}\left[H^{+}\right]\left[{\mathit{OH}}^{-}\right]$$ (47)

Since, [Na₃PO₄]_0, the only alkali component present in the system, dissociates completely into solution as phosphate ion, the contribution of the dissociation of [Na₃PO₄]₀ can be directly added to the initial concentration of [PO₄^3-]. During numerical integration, the initial concentrations/conditions for each species starting from Eqs. (34), (35), (36), (37), (38), (39), (40), (41), (42), (43), (44), (45), (46), (47) are set to 0, 0, 0, [Na₃PO₄]₀, [H₃C]₀, 0, 0, 0, [H₃B]₀, 0, 0, 0, 10⁻⁷, 10⁻⁷ respectively. [Na₃PO₄]₀, [H₃C]₀, [H₃B]₀, are the total concentrations of tri-sodium phosphate, citric acid and boric acid, respectively, present in the mixture. The concentration of [Na₃PO₄]₀, was varied for each experiment to simulate the experimental data.

3. Results

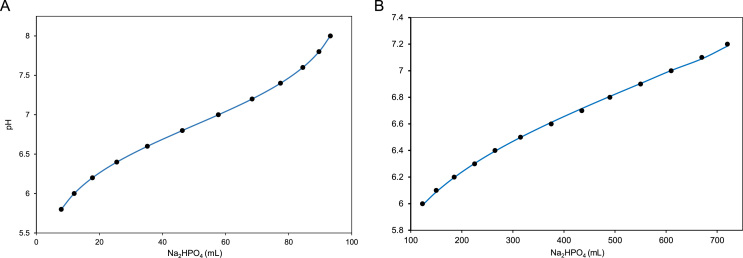
Experimental pH profiles for the standard phosphate buffer within the pH range 6–7.2 (Table 1) and 5.8–8 (Table 2) are available in molecular biology protocols [7]. In this experimental protocol, 0.1/1.0 M solution of mono sodium phosphate was mixed with 0.1/1.0 M di-sodium phosphate at specified ratios to prepare buffer solutions of desired pH [7]. At the outset, we tried to simulate the pH profile that would closely resemble the experimental pH profile, using the standard pK_a of phosphoric acid, i.e. 2.1, 7.2, 12.0. The simulated profile and the experimental profile showed discrepancy due to the fact that the standard values obtained from literature need not necessarily correlate with the optimized set of pK_a values that pertains to the experimental condition. In order to minimize the difference between the experimental and simulation we directly fitted the experimental data to the phosphate model by varying the pK_a values. In-house written matlab codes were used to perform the optimization of pK_a values. The curve fitting yielded an optimized pK_a values of 2.239, 6.864, 11.627 for phosphoric acid in a phosphate buffer prepared using 0.1 M stock solution. Similarly the optimized, pK_a values of 2.15, 6.8537 and 8.768 were obtained for phosphoric acid in a phosphate buffer prepared using 1 M stock solution. The pH profiles optimized using dynamic approach were in excellent agreement with the experimental values with a maximum deviation of 0.001 pH units at pH 7.6 and 0.015 pH units at pH 7.2 for 0.1 M and 1 M buffer solution, respectively (Fig. 2).

Table 1.

The pH profile of the 1 M phosphate buffer prepared by mixing different ratios of 1 M NaH₂PO₄ and 1 M Na₂HPO₄, The experimental values are model fitted using dynamic approach and the back-calculated pH values based on optimized pKa values are tabulated below.

Solution "A" (mL)	Solution "B" (mL)	1 M Phosphate buffer (pH)
(1 M NaH2PO4)	(1 M Na2HPO4)	Experimental	Back calculated
877	123	6.0	5.989
850	150	6.1	6.088
815	185	6.2	6.196
775	225	6.3	6.302
735	265	6.4	6.395
685	315	6.5	6.498
625	375	6.6	6.611
565	435	6.7	6.716
510	490	6.8	6.807
450	550	6.9	6.905
390	610	7.0	7.003
330	670	7.1	7.102
280	720	7.2	7.188

Table 2.

The pH profile of the 0.1 M phosphate buffer prepared by mixing different ratios of 0.1 M NaH₂PO₄ and 0.1 M Na₂HPO₄, The experimental values are model fitted using dynamic approach and the back-calculated pH values based on optimized pKa values are tabulated below.

Solution "A" (mL)	Solution "B" (mL)	0.1 M Phosphate buffer (pH)
( 0.1 M NaH2PO4)	( 0.1 M Na2HPO4)	Experimental	Back calculated
6.80	93.20	8.00	8.000
10.40	89.60	7.80	7.799
15.50	84.50	7.60	7.601
22.60	77.40	7.40	7.399
31.60	68.40	7.20	7.200
42.30	57.70	7.00	7.000
53.70	46.30	6.80	6.800
64.80	35.20	6.60	6.600
74.50	25.50	6.40	6.399
82.20	17.80	6.20	6.201
88.00	12.00	6.00	6.000
92.10	7.90	5.80	5.800

Fig. 2.

The experimental (•) and model fitted (—) pH profile of phosphate buffer prepared by mixing different volumes of equimolar concentrations of NaH₂PO₄ and Na₂HPO₄. (A) Shows the pH profile of 0.1 M phosphate buffer prepared by mixing mono and di sodium salt of phosphate. The experimental data was fitted to phosphate buffer model and optimized pKa values such as 2.239, 6.864, and 11.627 were obtained. (B) Shows the pH profile of 1 M phosphate buffer prepared by mixing mono and di sodium salt of phosphate. The experimental data was fitted to phosphate buffer model and optimized pKa values such as 2.15, 6.8537 and 8.768 were obtained.

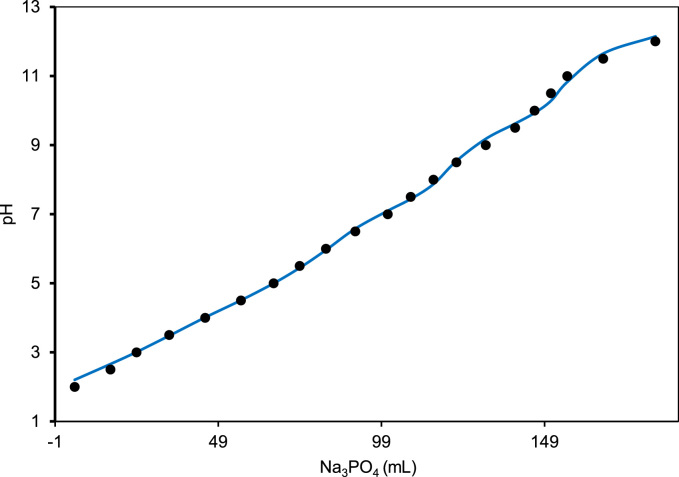
Titrated pH profile for universal buffer within the pH range 2–12 (Table 3) is obtained from earlier literature [1]. As seen for phosphate buffer, the simulated pH profile of universal buffer also showed discrepancy with the experimental value when standard pK_a values (Citric acid: 3.1, 4.7, 5.4; Boric acid: 9.2, 12.4, 13.3) were used, owing to the fact that pK_a values are sensitive to ionic concentration and temperature [1]. To minimize the difference between the simulated profile and the experimental data, we optimized the pK_a values through curve fitting using dynamic model. The optimized pK_a values for phosphoric acid were 3.259, 7.029, 12.233. The optimized pK_a values for citric acid were, 2.628, 4.431, 5.620, and the optimized pK_a values for boric acid were and 9.770, 12.507, 12.92. The fitted pH profile using optimized pK_a values for phosphoric, citric and boric acid agreed well with the experimental data with a maximum deviation of only 0.22 pH unit for pH 10.5 (Fig. 3).

Table 3.

The pH profile of the universal buffer prepared by mixing different ratios of 0.2 M Boric Acid+0.05 M Citric Acid and 0.1 M Na₃PO4, The experimental values are model fitted using dynamic approach and the back-calculated pH values based on optimized pKa values are tabulated below.

Solution "A" (mL)	Solution "B" (mL)	Universal buffer (pH)
(0.2 M Boric Acid+0.05 M Citric Acid)	0.1 M Na3PO4	Experimental	Back calculated
195	5	2.0	1.918
184	16	2.5	2.607
176	24	3.0	2.988
166	34	3.5	3.475
155	45	4.0	4.010
144	56	4.5	4.510
134	66	5.0	5.000
126	74	5.5	5.449
118	82	6.0	5.963
109	91	6.5	6.580
99	101	7.0	7.101
92	108	7.5	7.441
85	115	8.0	7.874
78	122	8.5	8.540
69	131	9.0	9.181
60	140	9.5	9.622
54	146	10.0	9.933
49	151	10.5	10.279
44	156	11.0	10.809
33	167	11.5	11.597
17	183	12.0	12.047

Fig. 3.

The experimental (•) and model fitted (—) pH profile of universal buffer prepared by titrating Na₃PO₄ (0.1 M) against a mixture of citric acid (0.05 M) and boric acid (0.2 M). The optimized pKa values for phosphoric acid were 3.259, 7.029, 12.233, citric acid were 2.628, 4.431, 5.620 and boric acid were 9.770, 12.507, 12.920.

4. Discussion

It is natural for the simulated pH profiles to deviate from the experimental pH profiles, when standard pK_a values are used in the calculation. Appropriate correction factors are to be incorporated to the standard pK_a values before any comparison is made between the simulation and the experimental pH profiles. Such discrepancies arise largely due to the dependence of pK_a on physical factors such as ionic strength and temperature. The explicit expression for pK_a is given as pK_a=–log₁₀(K_A); where K_A is the equilibrium constant of the dissociation process [12]. In general, the K_A is calculated from the ratio of concentrations of product to reactants, i.e. $K_A=\frac{\prod _{i=1}^m[P_i]}{\prod _{j=1}^n[R_j]}$. Here, P_i are the products of the reaction, R_j are the reactants of the reaction; n and m are the number of reactants and products involved in the reaction, respectively. $\prod _{i=1}^m$, $\prod _{j=1}^n$represents the multiplication of each terms whose index goes from i=1 to m or j=1 to n for reactant and products, respectively. Practically, due to ionic nature of the P_i and R_i, the concentrations [P_i] and [R_i], ought to be replaced with activities $\left\{P_i\right\}$ and $\left\{R_i\right\}$[13], which are represented as the multiplication of activity coefficient (γ_Pi) with the respective concentrations ([P_i]) i.e. $\left\{P_i\right\}$ = γ_Pi [P_i] and $\left\{R_i\right\}$ = γ_Ri [R_i]. To obtain accurate pK_a values which compares well with the experimental results for the simulations, ${K_A}^{\ominus }$, the thermodynamic equilibrium constant, should be used instead of K_A. The mathematical expression that relates ${K_A}^{\ominus }$ with K_A is, ${K_A}^{\ominus }=\frac{\prod _{i=1}^m[{\mathit{\gamma }}_{P_i}]}{\prod _{j=1}^n[{\mathit{\gamma }}_{R_j}]}\times \frac{\prod _{i=1}^m[P_i]}{\prod _{j=1}^n[R_j]}={\mathit{\gamma }\mathit{K}}_A$. If $\mathit{\gamma }$, the cumulative activity coefficient, can be determined experimentally, then the correction factor due to ionic strength at high concentrations can be easily incorporated in to the pK_a value. In the case of phosphate buffer, the standard pKa value for the dissociation of di-anionic phosphate to tri-anionic phosphate is around 12.0; whereas, the optimized pKa value for 0.1 M and 1 M phosphate buffer were, 11.6 and 8.8, respectively. A significant decrease of ~2.8 pH units observed for the optimized pKa value in the case of 1 M phosphate buffer, in comparison with the standard value, is largely due to the increased ionic effect seen at high concentration of the buffer solutions.

In addition to ionic activity, temperature also affects the value of thermodynamic equilibrium constant, ${K_A}^{\ominus }$[14]. The relationship between temperature T and ${K_A}^{\ominus }$ is given by ${\mathit{\Delta }G}^{\ominus }=-\mathit{RT}\ln {K_A}^{\ominus }$[10]. Where, ${\mathit{\Delta }G}^{\ominus }$, is the Gibbs free energy, R is the Gas constant. Temperature dependent correction factors are also needed be incorporated in to pK_a, when ${\mathit{\Delta }G}^{\ominus }$ and T are known. By making appropriate corrections to pK_a based on ionic activity and temperature effect, pH profiles that closely resembles the experimental values can be realized. In our case, we directly fitted the experimental data to the buffer models based on dynamic approach to obtain optimized pK_a values, circumventing the need for calculating the correction factors due to ionic and temperature effect. The optimized pK_a values are infact a self-corrective pK_a that implicitly takes into account the combined effects of ionic strength and temperature.

During numerical simulation of pH profile using dynamic approach, in addition to using optimized pK_a values, it is also necessary to evolve the system of differential equations for a longer period of time. If we let the differential equations to evolve for a shorter time period, the resulting solutions will only represent a pre-steady state condition which is still dynamically varying with time rather than the final equilibrium state. Hence, it is quint essential to evolve the system of differential equations for a longer period of time (e.g.>10¹⁵ s) so as to attain accurate pH values at equilibrium condition.

Conflict of interest

The authors declare no conflict of interest.

Appendix A. Supplementary material

Supplementary material: Supporting Information contains the explicit derivation of equations to predict pH profiles for mono-protic acid. Matlab codes to derive the symbolic expression for mono-protic acid, Di-protic acid, phosphate buffer and universal buffer using algebraic method. Matlab code to simulate the pH profiles for mono-protic acid, mono-alkaline compound using algebraic method is provided. Matlab code to predict the pH profiles for mono-protic acid using dynamic approach is also provided. Matlab code to perform curve-fit for the experimental phosphate buffer data is provided.

.