Abstract
Purpose
X‐ray scatter is a significant barrier to image quality improvements in cone‐beam computed tomography (CBCT). A moving blocker‐based strategy was previously proposed to simultaneously estimate scatter and reconstruct the complete volume within the field of view (FOV) from a single CBCT scan. A blocker consisting of lead stripes is inserted between the X‐ray source and the imaging object, and moves back and forth along the rotation axis during gantry rotation. While promising results were obtained in our previous studies, the geometric design and moving speed of the blocker were set empirically. The goal of this work is to optimize the geometry and speed of the moving block system.
Methods
Performance of the blocker was examined through Monte Carlo (MC) simulation and experimental studies with various geometry designs and moving speeds. All hypothetical designs employed an anthropomorphic pelvic phantom. The scatter estimation accuracy was quantified by using lead stripes ranging from 5 to 100 pixels on the detector plane. An iterative reconstruction based on total variation minimization was used to reconstruct CBCT images from unblocked projection data after scatter correction. The reconstructed image was evaluated under various combinations of lead strip width and interspace (ranging from 10 to 60 pixels) and different moving speed (ranging from 1 to 30 pixels per projection).
Results
MC simulation showed that the scatter estimation error varied from 0.8% to 5.8%. Phantom experiment showed that CT number error in the reconstructed CBCT images varied from 13 to 35. Highest reconstruction accuracy was achieved when the strip width was 20 pixels and interspace was 60 pixels and the moving speed was 15 pixels per projection.
Conclusions
Scatter estimation can be achieved in a large range of lead strip width and interspace combinations. The moving speed does not have a very strong effect on reconstruction result if it is above 5 pixels per projection. Geometry design of the blocker affected image reconstruction accuracy more. The optimal geometry of the blocker has a strip width of 20 pixels and an interspace three times the strip width, which means 25% detector is covered by the blocker, while the optimal moving speed is 15 pixels per projection.
Keywords: cone‐beam CT , imaging artifacts, moving blocker, optimization, scatter correction
1. Introduction
Cone‐beam computed tomography (CBCT) mounted on the gantry of a linear accelerator has recently become an instrumental part of volumetric image guidance in radiation therapy.1, 2, 3, 4 However, due to the broad beam geometry used in these systems, the presence of scatter contamination within the projection data decreases image quality by introducing image artifacts, reducing contrast, and limiting CT number accuracy, especially for sites requiring a large field of view (FOV). Previous studies have shown that the scatter‐to‐primary ratio (SPR) of photons in CBCT is high, even exceeding 100% for a large cone angle and large imaging object.5, 6 A method is needed to reduce the effects of scatter, improve image quality and maximize the usefulness of on‐board CBCT imaging systems such as dose calculation in adaptive therapy strategies.7, 8
Various strategies have been proposed to estimate the scatter signal in projection images including analytical calculation,9, 10, 11, 12, 13, 14, 15, 16, 17 Monte Carlo (MC) simulation18, 19, 20, 21, 22, 23 and beam blocker‐based techniques.24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40 Analytical calculation methods employ a kernel to decompose a measured projection into the scatter and primary components. These methods are fast and yield improved image quality, but their efficacy may be affected by heterogeneous media if a simple scatter kernel is used. Scatter kernels are different for different media because of the difference in scatter attenuation (scatter photons attenuated by surrounding medium) and the difference in contributions from high‐order scattering (multiple scattering in surrounding medium) in different geometries.11 For more accurate scatter estimation in this situation, an adaptive scatter kernel superposition may be employed.14 MC simulation provides good scatter estimation, but low computational efficiency prevents its routine application. Baer and Kachelrieß developed a hybrid scatter correction method, based on both MC simulations and a convolution‐based scatter correction algorithm.23
In beam blocker‐based methods, a blocker is used to hinder the X‐ray beams between a source and an object; the detected signal under the blocked region is attributed to scatter. As scatter is a low‐frequency smooth signal,19 its presence in unblocked regions can be estimated through interpolation from the scatter in blocked regions. These methods can be divided into two major schemes: stationary blockers and moving blockers. For stationary blockers, most methods require dual scanning,24, 25, 26 full fan27or a small imaging FOV.26, 28 The dual scanning scheme has been tested to avoid missing information caused by the blocker. A prior image‐based method measured the scatter distribution with partially blocked projection data taken on the initial treatment day using a blocker.24 The estimated scatter distribution was used to correct subsequent CBCT scans of the same patient. This approach needs an extra scan to generate the prior image and its accuracy depends on image registration techniques. The stationary blocker technique proposed by Lee et al. depends on data redundancy in the projection data acquired in full‐fan scan geometry.28 It is not applicable to the half‐fan acquisition geometry for imaging a large object, where the scatter artifact is more prominent as compared to a small object. Other stationary blocker approaches, such as the collimator‐shadow continuation method, measure the scatter signal from the blocked edge of the detector panel. This method has limited accuracy in estimating the scatter signal away from the detector boundary and involves a reduction in the maximum longitudinal FOV due to the z‐collimators impinging on the detector.29 Another stationary blocker approach, using peripheral detection of scatter and compressed sensing scatter retrieval, has been proposed for scatter estimation. Although the proposed method refined the scatter estimation with sophisticated optimization algorithm, the imaging volume is still reduced due to the stationary blocker and the performance largely depends on the precomputed scatter model.30 In recent years, a scatter correction method using primary modulation technique was proposed and developed.31, 32, 33, 34, 35, 36, 37 A calibration sheet with spatially variant attenuating materials is inserted between the X‐ray source and the object. Part of the primary distribution is modulated by the attenuation pattern of the modulator, and it is separated from the scatter. This method is computationally efficient, provides scatter correction using a single scan acquisition and can be applied to C‐arms devices.36, 37 However, the performance of the primary modulation method depends on optimized system parameters and materials of the primary modulator.32, 33, 34 For the moving blocker, most studies involve primary signal interpolation.38, 39, 40 Interpolation can generate an accurate estimate of the scatter signal because of its smoothness within a projection.25, 29 However, interpolating the primary signal may introduce large errors into reconstruction since high‐frequency signals such as sharp boundaries or edges are often present. Recently, a scatter estimation method in CBCT with striped ratio grids was proposed, preliminary investigation shows that striped ratio grids is able to improve the performance of the conventional anti scatter grid.41
We have proposed a scatter correction strategy based on a moving blocker system.42 Scatter signals in unblocked regions were estimated by interpolating the measured scatter signals in blocked regions. Instead of estimating the missing primary signal of the blocked region through interpolation, only the primary signal in the unblocked regions was used to reconstruct the CBCT image. This method can simultaneously estimate the scatter signal and reconstruct the complete volume within the FOV from a single scan. This method is not limited to full‐fan scan geometry or small FOV size, but can be applied to half‐fan scan geometry and large FOV size. Our previous work has demonstrated the effectiveness of the moving blocker strategy by constructing a moving blocker system and integrating it into a LINAC on‐board kV CBCT system.43 While the experimental work showed that the proposed moving blocker system can successfully estimate the scatter signal and obtain the entire volume within the FOV of a flat panel imager, the geometry and the moving speed of the blocker were set empirically.
In this study, we systematically investigated how variations in the design and the speed of the moving blocker affect imaging performance. We used MC simulation to generate projections of a pelvis phantom using CBCT geometry, and conducting physical experiments to integrate a moving blocker system into a LINAC on‐board kV CBCT system using a pelvis protocol (120 kVp and 80 mA/20 ms per projection) which is used on a Elekta machine in our clinic for patient setup purpose. The effective dose for one scan with this protocol is 4.95 mSv.44 We evaluated the performance in scatter estimation and image reconstruction accuracy under various combinations of width and separation of the lead strips at different moving speeds. Scatter estimation accuracy was quantified as a relative mean squared error by comparing the interpolated scatter to the MC simulated scatter. The reconstruction accuracy for each condition was quantified as a CT number error in comparison to a CBCT image reconstructed from unblocked full projections and scatter‐free data.
2. Materials and methods
2.A. Blocker design
The design of the lead strips and the geometric setup of the moving blocker for CBCT imaging are illustrated in Fig. 1. The blocker consisted of equally spaced lead strips of 3.2 mm in thickness. In our study, various combinations of strip width and interspace were investigated. The lead strips of the blocker were aligned perpendicularly to the gantry rotation axis z on a 3 mm thick acrylic board (120 × 180 mm) and moved back and forth along axis z, as indicated in Fig. 1(c).
Figure 1.
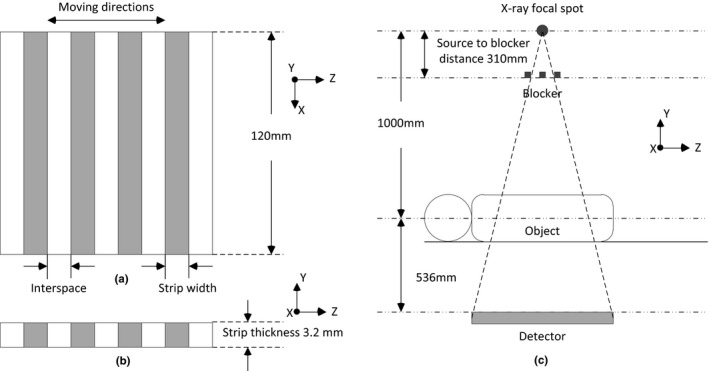
Illustration of the blocker and its location in an on‐board imaging system. (a) Anterior view of the blocker. (b) Cross section view of the blocker. (c) A blocker is inserted between the X‐ray source and the imaging object and moves back and forth along the gantry rotation axis z during CBCT acquisition. The source‐to‐blocker distance is 310 mm, the source‐to‐axis distance is 1000 mm while the source‐to‐detector distance is 1536 mm.
2.B. Simulation Studies
The MC simulation toolkit used in this study is called gDRR45 and is based on the physics relative to the kV CBCT energy range, namely the Rayleigh scatter, the Compton scatter, and the photoelectric effect. An effective source model was used to generate source photons representing the beam by a poly‐energetic spectrum. The accuracy of photon transport in this package has been previously demonstrated by comparing simulation results with those from EGSnrc,46 and indirectly by comparing the computed radiation dose with the measurements.47
The spectrum used in our study was poly‐energetic at 125 kVp and the number of photons was 5.0e + 9 per projection. Based on the study of Xu et al.,21 for pelvis phantom at half‐fan mode, the error in the simulation of scatter is about 3%. A point source was employed while the focal spot size of X‐ray source was neglected and the X‐ray source model was validated according to a Varian scanning protocol. The source‐to‐blocker distance was 310 mm, the source‐to‐detector distance was 1536 mm and the source‐to‐axis distance was 1000 mm [Fig. 1(c)]. The MC‐simulated projection was 512 × 512 with a pixel size of 0.8 × 0.8 mm2. The lead strip width and the interspace varied from 0.8 to 16 mm, corresponding to 5 pixels to 100 pixels projected at the detector panel plane.
2.B.1. Scatter estimation
The MC simulated scatter data was first smoothed by the noise removal strategy proposed by Jia et al.45 For one projection image, the scatter signal detected in the blocked region was used to estimate the scatter component in the unblocked region using cubic B‐Spline interpolation since the scatter is mostly low‐frequency signal.25, 29 To study the penumbra effects of the strips, a ray‐tracing technique was employed.48, 49, 50 In our scatter estimation study by MC simulation, we only considered the penumbra effects introduced by lead strip thickness. Two pixels adjacent to the each edge of the strip were excluded. To quantitatively evaluate the accuracy of the scatter estimation, we computed the relative root mean squared error of scatter (rRMSE) in unblocked regions of the detector by comparing the interpolated scatter to the MC simulated scatter:
| (1) |
where and denote the interpolated scatter and the MC simulated scatter at the detector pixel (u,v) in the unblocked region, respectively. indicates the projection angle.
2.B.2. CBCT reconstruction (scatter free)
For the reconstructed images from partially unblocked projections, we first focused on the influence of geometry and blocker moving speed. Scatter estimation inaccuracy was considered in the next section. These partially unblocked projections were based on the simulated scatter‐free data and generated by simulating the blocker motion during CBCT. Scatter‐free data were primary logarithm‐transformed projection data (i.e., line integral) of the pelvis phantom simulated by analytical method.48, 49 A total of 660 views were simulated over a 360° arc. The projection data of each view consisted of 512 × 512 pixels with an individual detector element size of 0.8 × 0.8 mm2. After the noise‐free line integrals l(u,v,θ) were calculated, the noisy primary signal I’(u,v,θ) was generated at each detector pixel (u,v) according to the following noise model:51, 52
| (2) |
where I 0 is the incident X‐ray intensity and is the background electronic noise variance. The X‐ray source was modeled as monochromatic. I 0 was chosen as 1 × 106 (number of photons) and was chosen as 10 empirically.42
A standard total variation regularized iterative reconstruction algorithm42, 53, 54 was adopted to reconstruct the CBCT image, where the projection data under the blocker was excluded during the updating. The algorithm was formulated by a constrained optimization model under the framework of compressed sensing. The number of iterations for the steepest gradient descent step is set to 10 and the number of iterations for the algebraic reconstruction step is set to 20 empirically in this study.42, 55
Qualitative and quantitative comparisons were performed between reconstructions with and without a blocker using anthropomorphic pelvis phantoms. The reconstructed images were generated with 256 × 256 × 140 voxels, with a voxel size of 2 × 2 × 2 mm3. All of reconstructed images were converted to Hounsfield units (HU). The root mean square error (RMSE) was used as a quantitative measure. Denoting the reconstructed image of partially unblocked projections as V , and the ideal reconstruction as V 0 , the RMSE is defined as
| (3) |
where are the coordinates of the reconstructed image. The ROI was chosen as the whole pelvis region of each slice where the background is excluded through a simple threshold‐based segmentation, and the central 100 (out of 140) slices were used for calculation.
2.B.3. CBCT reconstruction (scatter corrected)
We could ideally use MC to simulate the projection data for all geometric design combinations of the blocker and then reconstruct CBCT images. However, in order to investigate CBCT reconstruction after scatter correction in a more efficient way, we used a residual interpolation technique in our MC simulation study. In the unblocked region, the estimated scatter signal S’ was compared to the simulated scatter signal S . The scatter estimation error is S ‐ S’ . The relative error of log‐transformed projection signals (i.e., line integrals) introduced by scatter estimation error is:
| (4) |
where denote the detector coordinates and θ denotes the gantry angle; I 0 is the incident X‐ray intensity and P is the primary signal generated by MC simulation. The extreme values of such as those below 0.8 and beyond 1.2, were excluded empirically. Additionally, relative values in the unblocked region were interpolated to the blocked regions to obtain the whole relative value map.
To improve the efficiency, CBCT projection data were simulated at sparse angles. The relative value map was then interpolated to other projection angles. As reported by Xu et al., for the pelvis phantom using the same scanning geometry, when the simulated projection number is more than 15, the error of estimated scatter signal caused by interpolation among different projection views is less than 1%.21 In this study, we chose projection number 36 to obtain sufficiently accurate scattered signals. The 36 projections were evenly distributed over a 360⁰ arc. Therefore, we got 36 relative value maps (). For each scan, we acquired 660 projections in the physical experiment. Thus we estimated 660 relative error maps by interpolating the 36 maps obtained from MC simulation.
The log‐transformed projection measurements influenced by the scatter estimation error can be expressed from in Eq. (2) and in Eq. (4) as:
| (5) |
CBCT Images with scatter correction were reconstructed from projection data.
In this step, we considered the penumbra effects introduced by lead strip thickness and blocker movement. The lead strip thickness (3.2 mm) leads to 2‐pixel penumbra of each strip edge. The number of affected pixels was different for different blocker moving speed. For example, if the blocker moving speed is 10 pixels per projection (8.8 mm s−1) and the exposure time is 20 ms (section 2.C.2), each strip edge leads to 2‐pixel moving penumbra according to the distance of blocker to detector plane. The total penumbra around each strip edge is 4 pixels for blocker moving speed at 10 pixels per projection. If the moving blocker speed is 20 or 30 pixels per projection (17.6 or 26.4 mm s−1), the total penumbra around each strip edge is 5 or 6 pixels. In the MC simulation studies, the total penumbra around each strip edge was set to be 4, 6, and 8 pixels for blocker moving speeds below 10, 10–20, and 20–30 pixels per projection, respectively. In physical experiments, 8 pixels were excluded around each strip edge for simplicity. The regions adjacent to the edges of the strip were excluded in scatter estimation and reconstruction. For example, if the blocker had a strip width of 1.6 mm and an interspace of 3.2 mm, it would correspond to each blocked region with 10‐pixel‐wide, and each unblocked region with 20‐pixel‐wide at the detector plane. If the blocker moving speed was 15 pixels per projection (13.2 mm s−1), 6 pixels around the strip edge were excluded (Fig. 2). Therefore, we obtained a 4‐pixel‐wide blocked region for scatter estimation and a 14‐pixel‐wide unblocked region for reconstruction after scatter correction. We also used Eq. (3) to compare the CBCT reconstructed image after scatter correction to image reconstructed from non‐blocked and scatter‐free projections.
Figure 2.
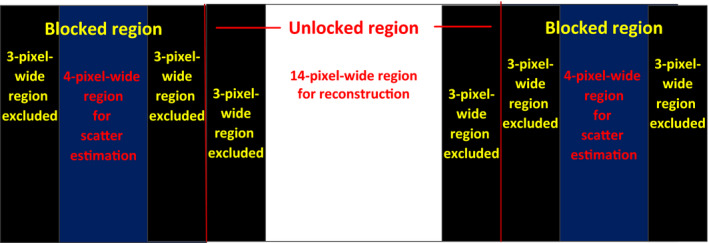
Part of the detector plane to illustrate of the excluded pixels for eliminating penumbra. The blocker has a strip width of 1.6 mm and an interspace of 3.2 mm, corresponding to a 10‐pixel‐wide blocked region and a 20‐pixel‐wide unblocked region at detector plane. The blocker moving speed is 15 pixels per projection (13.2 mm s−1), 6‐ pixel‐wide region around the strip edge were excluded.
2.C. Experimental studies
2.C.1. Setup of the moving blocker system
In the experimental study, all CBCT scans were acquired on the XVI system of an Elekta Agility accelerator. The parameters of the moving blocker system and imaging system are summarized in Table 1. A beam attenuation blocker was inserted between the X‐ray source and the object to measure the scatter signal [Fig. 1(c)]. In our experiment, the motion control equipment was connected to move the blocker back and forth along the rotation axis during CBCT acquisition. The moving blocker system installed on the arm of the kV source is shown in Fig. 3(a). The moving blocker system used in this study is similar to that used in our previous study.43 The system is composed of a lead‐strip blocker [labeled (A) in Fig. 3(a)], a linear motion guide actuator [labeled (B) in Fig. 3(a)] (KR20, THK CO., LTD. Tokyo, Japan), and a bipolar stepper motor with a controller [labeled (C) in Fig. 3(a)] (PD42‐3‐1141, TRINAMIC, Hamburg, Germany). Three blockers, consisting of equally spaced lead strips embedded on a 3 mm thickness acrylic board (120 × 180 mm), were used as shown in Fig. 3(b). The lead strips were 3.2 mm in thickness, 3.2 mm in width and were placed with a 3.2 (A1), 6.4 (A2) and 9.6 (A3) mm pitches, respectively, for the three blockers. At the detector plane, the three blockers corresponded to each blocked region of 20 pixels width and each unblocked region of 20, 40, 60 pixels width, respectively. The choice of these blockers was based on the MC simulation results and the manufacture possibility. The lead strips of the blocker were aligned perpendicularly to the rotation axis, and consistently covered the entire FOV at a source‐to‐blocker distance of 310 mm [Fig. 1(c)]. For the linear motor used in this work, the maximum linear motion speed is 30 mm s−1, corresponding to a motion speed of 34 pixels per projection at the detector plane. Considering speed variation, direction changes and system stability, the linear motion speed of the blocker was set as 7, 13.2, and 20.2 mm s−1, which corresponded to a speed of 8, 15, or 23 pixels per projection at the detector plane in our experiment (Supplementary Video S1).
Table 1.
Parameters of the physical experiment
| Moving blocker parameters: | |
| Strip thickness | 3.2 mm |
| Strip width | 20 pixels (3.2 mm) |
| Gap width | 20, 40, 60 pixels (3.2, 6.4, 9.6 mm) |
| Imaging parameters: | |
| X‐ray energy | 120 kVp |
| Projection size | 512 × 512 pixels |
| Pixel size | 0.8 × 0.8 mm2 |
| Source to detector distance | 1536 mm |
| Source to blocker distance | 310 mm |
| Source to rotation axis distance | 1000 mm |
| Number of views | 660 |
| Rotation | Circular, 360⁰ |
| Scan mode | Half fan |
| Imaging panel offset | 115 mm |
| FOV | Medium |
| Bow‐tie filter | No |
| Reconstruction parameters: | |
| Reconstruction voxel size | 2 × 2 × 2 mm3 |
| Reconstruction volume size | 256 × 256 × 140 |
Figure 3.

(a) A customized moving blocker system mounted on an Elekta Synergy XVI system. Components of the moving blocker system are labeled as (a) a lead‐strip blocker (3.2 mm lead strip width and 3.2 mm interspace); (b) a linear motion guide actuator (KR20, THK); (c) a bipolar stepper motor with controller(PD1141, TRINAMIC). (b) Three customized blockers, lead strips were 3.2 mm in thickness and 20 pixels (3.2 mm) in width. Interspace was 20 pixels (3.2 mm) for A1, 40 pixels (6.4 mm) for A2 and 60 pixels (9.6 mm) for A3.
2.C.2. Measured phantom data
To evaluate the performance of the moving blocker system, an anthropomorphic pelvis phantom CIRS 801‐P (Computerized Imaging Reference Systems Inc., Norfolk, VA, USA) was used for CBCT acquisition. The pelvis phantom is a realistic tissue‐equivalent model designed for imaging and dosimetry applications.
Data acquisitions were performed on the integrated moving blocker CBCT system as described in Section 2.C.1. A 360⁰ arc rotation, medium FOV protocol was used to acquire CBCT of the anthropomorphic pelvis phantom with a M20 collimator (medium FOV) and a F0 filter (no bowtie filter). The X‐ray tube settings for this pelvis protocol were 120 kVp and 80 mA/20 ms. For each scan, approximately 660 projections were acquired in about 2 min. Each projection data contained 512 × 512 pixels with a pixel size of 0.8 × 0.8 mm2. Projection data were acquired using half‐fan with an imaging panel offset of 115 mm at a source‐to‐detector distance of 1536 mm (Table 1). A regular CBCT scan without the moving blocker was also acquired.
During CBCT acquisition of the moving blocker, the detected signal in the blocked region was used to estimate the scatter fluence in the unblocked region using cubic B‐Spline interpolation. To avoid the penumbra effect of the strips, 8 pixels were excluded around the strip edge. Therefore, the central 12‐pixel‐wide part of each blocked region was used for scatter estimation. Before interpolation, a 3 × 3 median filter was applied to exclude extremity values of the measured scatters and a 2D 9‐pixel moving average filter was used to further smooth the interpolated scatter maps.28 A primary signal was obtained in the unblocked region by subtracting the estimated scatter signal. The central 12‐, 32‐, 52‐pixel‐wide part of each unblocked region was used for reconstruction when using the three different blockers.
A line integral of each ray in the unblocked region was then calculated by logarithmic transformation. To obtain line integrals, an air scan was acquired with the moving blocker system, and the signal detected in the unblocked region was interpolated into the blocked region to obtain the air scan for the full FOV. About 660 interpolated projections were averaged every 10 degrees. Thirty six normalization maps could be obtained. Image reconstruction was then performed on the corrected partial unblocked projection data.
We selected three small ROIs in the reconstructed CBCT images to quantify reconstruction accuracy. The inaccuracy of CT number in CBCT was quantified by in the selected ROIs using the following equation:
| (6) |
Where is the index of the ROI, is the mean reconstructed value in HU inside the ROI, and is the corresponding value measured in the ground‐truth image.
3. Results
3.A. MC simulation study
3.A.1. Scatter estimate error
The MC simulation results on the scatter estimation error of three angles, employing different blockers are shown in Fig. 4. For simplicity, we used B and G to refer to the blocker strip width (B) and gap width (G). For example, B20G60 referred to a blocker with a strip width of 3.2 mm and a gap width of 6.4 mm, corresponding to each blocked region of 20‐pixel‐wide and each unblocked region of 60‐pixel‐wide at the detector plane. Similarly, we used pixels per projection instead of mm/s to describe the blocker moving speed. For example, a blocker moving at a speed of 8.8 mm s−1 corresponded to 10 pixels per projection at the detector plane. The conversion between these two speed units was easy to accomplish since we knew the source‐to‐blocker distance, the source‐to‐detector distance, the pixel size and the time of one rotation.
Figure 4.
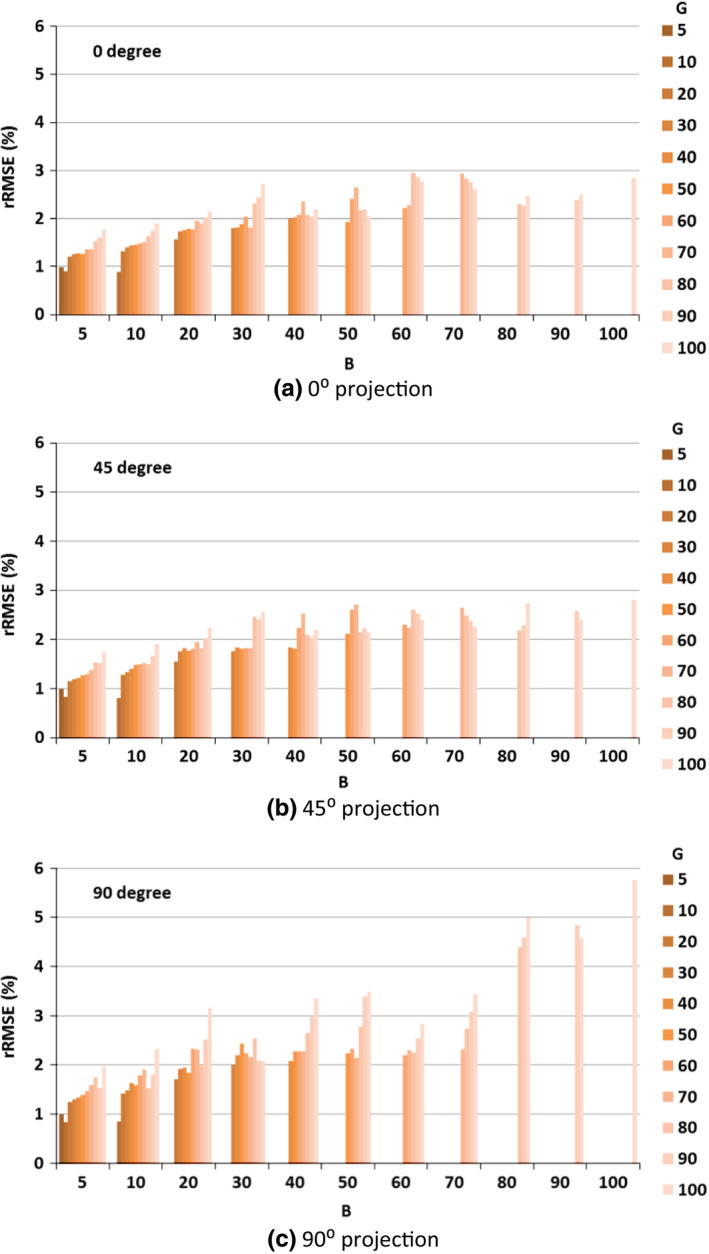
Scatter estimation error in the unblocked regions of detector panel, as both strip width and interspace varied from 5 to 100 pixels (as projected at the detector plane). (a) 0° projection (frontal); (b) 45° projection; (c) 90° projection (lateral).
The scatter estimation error in the unblocked regions of the detector was quantified by rRMSE as described in Eq. (1). Both lead strips width and interspace varying from 0.8 to 16 mm corresponded to 5 pixels to 100 pixels at the projected detector panel plane. The scatter estimation error varied from 0.8% to 5.8% with different combinations of lead strip width and interspace. The scatter estimation errors increased with increases in interspace or strip width (Fig. 4).
3.A.2. CBCT reconstruction (scatter free)
From the scatter estimation results (Section 3.A.1), we found that the error increased with an increase in interspace or strip width. For reconstruction error investigation, we only considered the situations of scatter estimation error lower than 2%. Additionally, considering the penumbra effect introduced by the strip thickness and blocker movement, excessively narrow strips may cause the whole blocked region to be affected by the penumbra, the blocker width of 5 pixels was not studied anymore. Therefore, from the reminder of this paper, we only studied the blockers of strip width 10/20 pixels (1.6/3.2 mm) and the interspace of 10–60 pixels (1.6–9.6 mm).
Axial (top row) and coronal slices (bottom row) of each reconstruction image of the simulated pelvis phantom are illustrated in Fig. 5. Slices of the image reconstructed from simulated full and scatter free projections as benchmarks are shown in Figs. 5(a) and 5(f). The RMSE of CBCT reconstruction from the projections of blocker B10G50 with a moving speed of 10 pixels per projection was 7.5 [Figs. 5(b) and 5(g)]. The CBCT reconstruction from the projections of blocker B20G20 with a moving speed of 20 pixels per projection has more artifacts (RMSE = 19.8, Figs. 5(c) and 5(h)). The CBCT reconstruction from the projections of blocker B20G20 with a moving speed of 1 pixel per projection, was even worse due to the artifacts (RMSE = 45.8, Figs. 5(d) and 5(i)). The difference images (Fig. 6) show that the errors caused by the partially blocked projections were different when using different blockers or moving at different speed. For blocker B10G10 with a moving speed of 20 pixels per projection, the reconstruction was missing some parts of the image, named reconstruction failure in this paper [Figs. 5(e) and 5(j)].
Figure 5.

Axial (top row) and coronal slices (bottom row) of the reconstruction from simulated data. (a) and (f): Benchmark, simulated non blocker image; (b) and (g): B10G50, speed 10 pixels per projection ( RMSE = 7.5); (c) and (h): B20G20, speed 20 pixels per projection ( RMSE = 19.8); (d) and (i): B20G20, speed 1 pixels per projection ( RMSE = 45.8); (e) and (j): B10G10, moving speed 20 pixels per projection ( RMSE = 202). Display window [−800, 1000] HU.
Figure 6.

Difference images between the reconstructed images from partially unblocked projections and reconstructed images from full projections. (a), (b) and (c): difference images between Figs. 5(b)–5(d) and Fig. 5(a); (d), (e) and (f): difference images between Figs. 5(g)–5(i) and Fig. 5(f); Display window [−350, 350] HU.
The RMSE of the CT number in the CBCT images reconstructed from partially unblocked projection datasets is reported in Fig. 7. The reconstruction accuracy improved as the interspace increased for a fixed strip width. The reconstruction error was higher for slower moving speed (1, 2, and 5 pixels per projection). For a blocker of fixed geometry, the best reconstruction was achieved at a moving speed of about 15 pixels per projection. Six reconstruction failures were observed in our simulation. All of them occurred when the moving speed was an integer multiple of the sum of the strip width and interspace (failure scenarios are not shown in Fig. 7). For a B10G10 blocker at a moving speed of 20 pixels per projection, this situation equaled the application of a stationary B10G10 blocker during the scan. Some parts of the object were constantly blocked during the whole scan and could not be reconstructed successfully [Figs. 5(e) and 5(j)].
Figure 7.
CBCT image reconstruction error when different moving blockers were applied; no scatter was presented. The blocker lead strip width was 10 and 20 pixels, the gap width was 10, 20, 30, 40, 50 and 60 pixels, and the blocker moving speed was from 1 pixel per projection to 30 pixels per projection. (We did not show the scenarios where RMSE is above 60).
3.A.3. CBCT reconstruction after scatter correction
In the second step, we compared CBCT reconstruction following scatter correction to those of the simulated scatter‐free images. Axial (top row) and coronal slices (bottom row) are illustrated for each reconstruction image of the anthropomorphic pelvis phantom (Fig. 8). Figs. 8(a) and 8(f) are same as Figs. 5(a) and 5(f). The reconstructed CBCT from the projections of blocker B10G50 with a moving speed of 10 pixels per projection after scatter correction are reported in Figs. 8(b) and 8(g). By comparing Figs. 5(g) and 8(g), we noticed artifacts (yellow arrow) introduced by the scatter residual.
Figure 8.
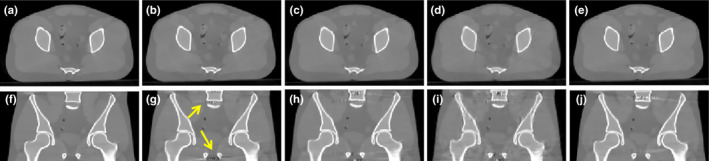
Axial (top row) and coronal slices (bottom row) of the reconstruction from simulated data. (a) and (f): Benchmark, simulated non blocker and scatter free image; (b) and (g): B10G50, speed 10 pixels per projection( RMSE = 28.9); (c) and (h): B20G20, speed 20 pixels per projection( RMSE = 30.7); (d) and (i): B20G20, speed 1 pixels per projection( RMSE = 54.5); (e) and (j): B20G60, moving speed 20 pixels per projection( RMSE = 28.2). Display window [−800, 1000] HU.
The RMSE of the CT number in the CBCT images reconstructed from partially unblocked projection datasets after scatter correction is illustrated in Fig. 9. In this step, we only investigated a strip width of either 10 or 20 pixels, with an interspace varying from 10 to 60 pixels. For a strip width of 10 pixels, the RMSE was almost below 40 [Fig. 9(a)]; for a strip width of 20 pixels, the RMSE was always below 70 except when the moving speed was an integer multiple of the sum of the strip width and interspace [Fig. 9(b)]. After introducing a scatter estimation error, the RMSE increased about 15 HU as compared to scatter‐free reconstruction images. The smallest RMSE was achieved when using blocker B10G30 at the speed of 15 pixels per projection.
Figure 9.
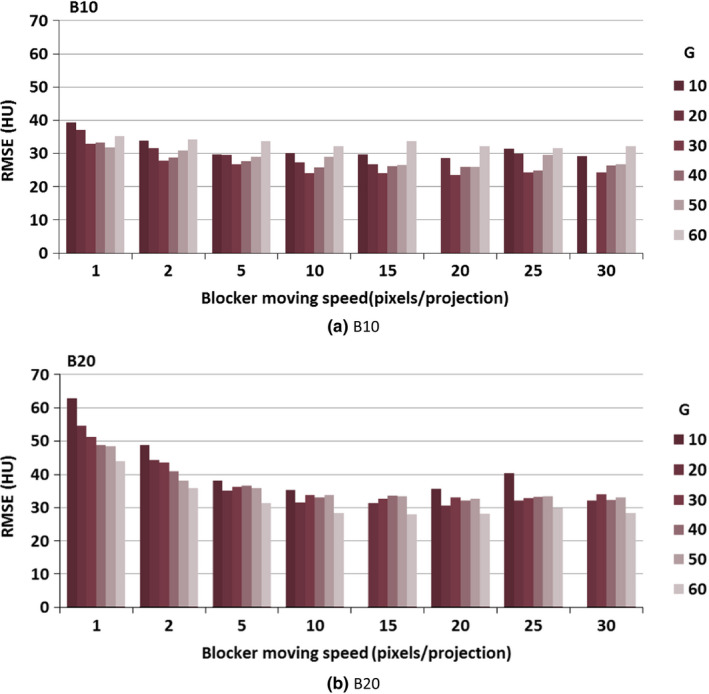
CBCT image reconstruction error upon application of different moving blockers. Simulations of the blocker lead strip width was 10 and 20 pixels, the gap width was from 10 to 60 pixels, and the blocker moving speed was from 1 to 30 pixels per projection. (We did not show the scenarios where RMSE was above 70).
By comparing Figs. 9(a) and 9(b), we did not find a major difference in RMSE between a strip width of 10 pixels and 20 pixels; the average difference was 5 HU. When the moving speed was over 5 pixels per projection, the RMSE did not change dramatically.
3.B. Physical experiments
Since the average RMSE difference between a strip width of 10 pixels and 20 pixels was only 5 HU, and considering the physical properties of lead and practicality to make a lead strip with straight edges, physical blockers were all made with strip width of 20 pixels (3.2 mm) for the experiment.
We conducted the physical experiments on an anthropomorphic pelvic phantom using three physical blockers at three moving speeds. Axial (top row) and coronal slices (bottom row) of each reconstruction image of the anthropomorphic pelvis phantom are illustrated in Fig. 10. Figs. 10(a) and 10(f) are same as Figs. 5(a) and 5(f). CBCT reconstruction from scatter contaminated projections are reported in Figs. 10(b) and 10(g) while those from scatter‐corrected projections are shown in Figs. 10(c) and 10(h); these are partially unblocked projections acquired with the moving blocker system B20G20 at a speed of 8 pixels per projection; Figs. 10(d) and 10(i) indicate CBCT reconstruction from scatter‐corrected, partially unblocked projections acquired with the moving blocker system B20G60 at a speed of 15 pixels per projection. Figs.10(e) and 10(j) gave the CBCT reconstruction results acquired from a Varian OBI system using a clinical pelvis protocol. Scatter correction and the reconstruction were conducted by Varian software. All images are displayed at the same window level. The image without the blocker and scatter correction was seriously degraded by shading artifacts caused by scatter contamination and radar artifacts due to the lag effect [Figs. 10(b) and 10(g)]. The image is much darker than the scatter‐free reconstructed image and the contrast was reduced heavily, especially for the central soft tissues. Following scatter correction, intensity and contrast were recovered to allow the soft tissue organs to be distinguished. The central region can be easily distinguished in Fig. 10(d) as compared to Fig. 10(b). Horizontal profiles as indicated by a yellow dashed line in Fig. 10(b) were compared in Fig. 11. Following scatter correction, the image intensity of the reconstructed CBCT image approached the intensity of the image reconstructed from the simulated non blocker scatter‐free projections. Shading and lagging effects were also corrected. The use of the moving blocker B20G60 at a speed of 15 pixels per projection yielded better results as compared to the moving blocker B20G20 at a speed of 8 pixels per projection. The result provided by Varian has similar performance as ours [Fig. 11]. Visually, less noise exists in the reconstructed images by Varian than that in our images [Figs.10(d), 10(i) and 10(e), 10(j)].
Figure 10.
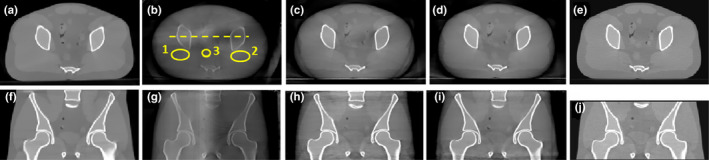
Axial (top row) and coronal slices (bottom row) of the anthropomorphic pelvis phantom. (a) and (f): Benchmark, simulated non blocker and scatter free image; (b) and (g): reconstruction from scatter‐contaminated projection data; (c) and (h): B20G20, speed 8 pixels per projection; (d) and (i): B20G60, speed 15 pixels per projection. (e) and (j): reconstruction provided by Varian OBI system, scatter corrected by asymmetric kernel approach provided in the software. The inferior‐superior length is different in the experiments of Elekta and Varian systems. Display window [−800, 1000] HU.
Figure 11.
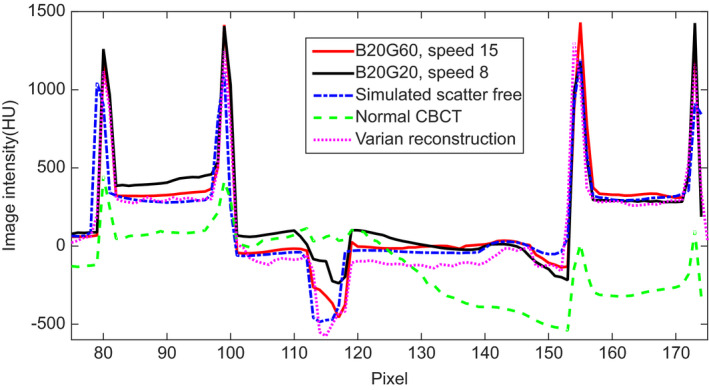
Comparison of the horizontal profile, as indicated by a dashed line in Fig. 10(b), for simulated non blocker and scatter free image, scatter contaminated CBCT, and scatter corrected CBCT images with two different moving blockers and with Varian software in Figs. 10(a)–10(e), respectively.
Table 2 summarizes the mean and standard deviation of CT number of ROIs delineated in Fig. 10(b), and the RMSE e between each CBCT reconstruction after scatter correction and the reconstruction from scatter free and non‐blocker projections. The RMSE e was reduced from 290 to less than 35 after scatter correction was performed in the partially unblocked projections acquired with the moving blocker system. From the results listed in Table 2., we found that all three blockers were effective in scatter correction at different moving speeds. Blocker B20G60 with a moving speed of 15 pixels per projection yielded the smallest RMSE e ; we consider this as the optimal moving blocker system design. From the standard deviation of CT number listed in Table 2, we found that the noise level in our scatter corrected images is higher than scatter free images. This is caused by residual scatter noise after correction. More details of this issue can be found in Zhu et al.'s work.56
Table 2.
Comparison of the CT number of three ROIs of the anthropomorphic pelvis phantom. For the proposed method, three blockers were used, they have the same strip width of 20 pixels (B20) and different gap width 20, 40, 60 pixels (G20, G40, G60), three moving speeds were used (8, 15, 23 pixels per projection)
| Blocker | Moving speed (pixels per projection) | ROI1 mean/stda | ROI2 mean/std | ROI3 mean/std | RMSE e |
|---|---|---|---|---|---|
| G20 | 8 | 102/44 | 106/45 | 54/12 | 35 |
| G20 | 15 | 89/40 | 98/45 | 51/13 | 30 |
| G20 | 23 | 100/43 | 104/46 | 55/12 | 34 |
| G40 | 8 | 74/39 | 96/56 | 42/8 | 26 |
| G40 | 15 | 72/43 | 93/50 | 40/11 | 25 |
| G40 | 23 | 73/38 | 103/55 | 35/5 | 25 |
| G60 | 8 | 76/41 | 102/43 | 31/7 | 22 |
| G60 | 15 | 76/40 | 95/44 | 12/6 | 13 |
| G60 | 23 | 64/30 | 94/47 | 21/7 | 19 |
| Varian scatter correction images | 62/32 | 75/17 | 5/9 | 15 | |
| No scatter correction images | ‐253/34 | ‐177/52 | ‐261/10 | 290 | |
| Simulated scatter free images | 88/13 | 79/12 | 3/5 |
Standard Variation.
The mean and standard deviation of CT number of ROIs obtained by MC simulation and physical experiments were compared in Table 3. Three blockers (B20G20, B20G40 and B20G60) were used at the moving speed of 15 pixels per projection. As we expected, B20G60 gives the best performance. RMSE e is smaller in MC simulation than that in physical experiment, because there are more system deviations and noise in real experiment.
Table 3.
Comparison of the CT number of three ROIs between MC simulation and physical experiment. Three blockers were used, they have the same strip width of 20 pixels (B20) and different gap width 20, 40, 60 pixels (G20, G40, G60), moving speed was 15 pixels per projection
| Blocker | MC simulation | Physical experiment | ||||||
|---|---|---|---|---|---|---|---|---|
| ROI1 mean/std | ROI2 mean/std | ROI3 mean/std | RMSE e | ROI1 mean/std | ROI2 mean/std | ROI3 mean/std | RMSE e | |
| G20 | 78/10 | 74/16 | 11/6 | 7.6 | 89/40 | 98/45 | 51/13 | 30 |
| G40 | 88/8 | 82/13 | 13/3 | 6.3 | 72/43 | 93/50 | 40/11 | 25 |
| G60 | 86/4 | 80/13 | 6/7 | 2.5 | 76/40 | 95/44 | 12/6 | 13 |
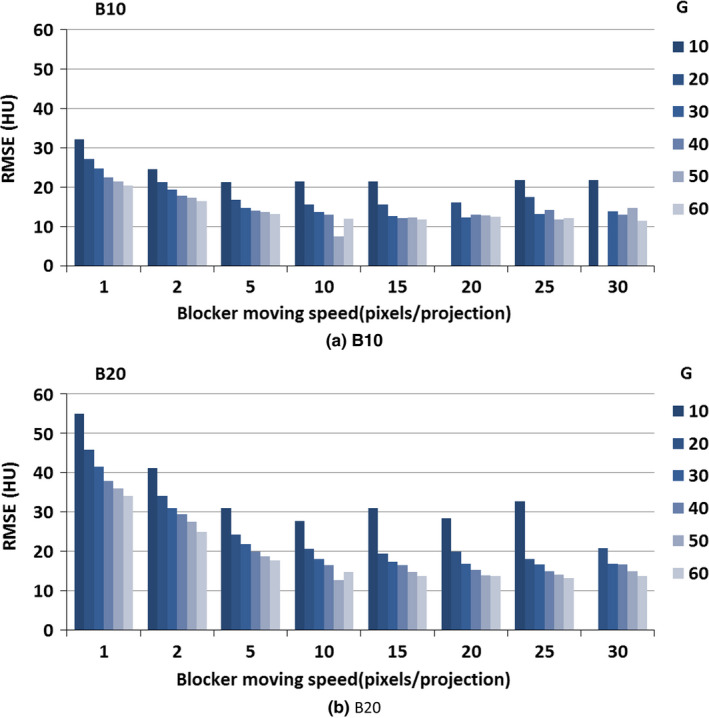
In the MC simulation, the moving speed of the blocker was set as a constant. However, in the real moving blocker system, speed is not a constant due to acceleration and deceleration as direction changes. In our experiment, the moving speed was reduced to about half of the set speed as direction changed, affecting 3~6 projections. We investigated CBCT reconstruction results by MC simulation when the blocker was moving at variable speed. We simulated a scenario where the blocker moving at an average speed of 15 pixels per projection with a variation range of 1~30 pixels per projection. Following scatter correction and reconstruction, the variable speed results were compared to those acquired at a constant speed of 15 pixels per projection. Speed variations did not deteriorate the reconstruction result (Table 4). In the real experiment, when the blocker changed moving directions, speed variations had little effect on reconstruction results.
Table 4.
Comparison of RMSE of the anthropomorphic pelvis phantom, different geometry design of blockers applied, blocker moving speed 15 pixels per projection, constant VS. various moving speed
| Blocker | B10 | B20 | ||
|---|---|---|---|---|
| Constant speed | Various speed | Constant speed | Various speed | |
| G10 | 29.7 | 31.1 | 67.0 | 48.6 |
| G20 | 26.8 | 24.2 | 31.4 | 33.5 |
| G30 | 24.1 | 21.6 | 32.7 | 28.9 |
| G40 | 26.2 | 28.6 | 33.6 | 33.4 |
| G50 | 26.6 | 17.9 | 33.4 | 27.0 |
| G60 | 33.7 | 44.0 | 28.0 | 40.0 |
4. Discussion and conclusion
In this work, we optimized the geometry and speed of a moving blocker system for CBCT scatter correction by conducting MC simulations and experiments. In our previous study, we verified the effectiveness of our proposed moving blocker system on scatter correction using both a Catphan phantom and a realistic pelvis phantom.43 In this study, we only investigated a large imaging volume for CBCT acquisition in a realistic pelvis phantom with a large cone angle characterized by scattering problems. First, we evaluated the scatter estimation accuracy when using different blockers. The scatter signal was simulated by MC calculation with various combinations of lead strip width and separation, ranging from 5 to 100 pixels at the detector plane. The scatter estimation error varied from 0.8% to 5.8% and increased with increased interspace and strip width.
Second, we investigated the effect on CBCT reconstruction introduced by partially blocked projections. We found that about 10~40 RMSE were introduced by partially blocked projections under different conditions. As expected, reconstruction was more accurate for wider interspace in a fixed strip width. Reconstruction may fail if the moving speed is an integer multiple of the sum of the strip width and interspace, equaling the application of a stationary blocker. In this situation, a certain region of the projections may have been constantly blocked throughout the whole acquirement procedure, and some voxels in the object could not be reconstructed successfully.
We combined the first two steps to study CBCT reconstruction after scatter correction by MC simulation with strip width of 10 and 20 pixels. When the moving speed was low (1, 2, 5 pixels per projection), CBCT reconstruction yielded a larger RMSE (Fig. 9). When the moving speed was over 10 pixels per projection, the moving speed did not impact reconstruction. We observed that the CBCT image reconstructed from the projections, acquired with a narrower‐strip‐wider‐interspace blocker, exhibited fewer artifacts (Fig. 7). A wider interspace can deliver more information for reconstruction, but may also decrease accuracy in scatter estimation. There should be a compromise between strip width and interspace. The smallest RMSE was acquired when blocker B10G30 was used at a speed of 15 pixels per projection (Fig. 9). The average difference in RMSE between strip widths of 10 and 20 pixels was about 5 HU. Based on our MC simulation results and considering the difficulty of making lead strips with a small width, we customized physical blockers with a 20 pixel strip width for experimental evaluation. The best reconstruction was acquired when blocker B20G60 was used at a speed of 15 pixels per projection.
In our work, the blocker moving speed was studied in relative speed (pixels per projection) in both simulation and experimental studies. The relative speed means how many pixels the blocker moved on the detector plane between two adjacent projections, which is a combination of four factors: absolute speed of the moving blocker (mm/s), rotation speed of the gantry (projections/s), distance from the blocker to detector and detector pixel size (mm). We can consider the relative speed (pixels per projection) as a general parameter. If the rotation speed of the gantry or distance from the blocker to detector changes, we only need adjust the absolute blocker moving speed to get the speed we need.
As seen in Table 2, the scatter corrected cone‐beam images have a relatively higher noise level than the simulated scatter free images. The increase in noise level mainly stems from the scatter noise which is left in the scatter corrected projections using our method. Because in our method, we considered scatter signal as low‐frequency signal, the detected signal in the blocked region was first smoothed and then interpolated to get the whole scatter field. The estimated scatter field is low frequency, so there will be some scatter noise left in the scatter corrected projections. The issue of uncorrected scatter noise is a general problem for all post‐processing scatter algorithms which correct for scatter after the scatter photons reach the detector.31, 32 Due to the randomness of the scattering event, the scatter noise cannot be totally suppressed. One possible way to achieve lower noise level is to increase mAs in practical applications. The dose to the patient does not increase because the blocker is inserted between the X‐ray tube and the patient.
The CBCT volume was reconstructed from 2D X‐ray projection images acquired over an arc using a flat‐panel detector (FPD) with an indirect detection of X‐ray photons. During the conversion of X‐ray photons to optical photons and optical photons to electric signal, a fraction of the signal was delayed, indicating this signal would be present in subsequent projections.57 In CBCT imaging (where a series of projection images is acquired), each projection is contaminated by a fraction of the previous X‐ray signal, generating image lag and/or ghosting. In pelvic imaging, the most prominent artifact introduced by image lag is a radar artifact and a corresponding gray value reduction on the right side of the phantom,58 resulting in an apparent left–right contrast [Figs. 10(b) and 10(g)]. Image quality also degraded from non‐idealities such as shading and streaking due to scatter and beam hardening, but the contrast between left and right mainly derived from image lag. Ren et al. simulated a synchronized‐moving‐grid system in CBCT which can correct both scatter fraction and lag effects.59 Although the motion pattern of the grid/blocker and the image reconstruction strategy were different in our study, the potential of using the moving grid/blocker for lag correction was the same as our moving blocker‐based scatter correction strategy. In our moving blocker system, measured signals from both blocked and unblocked regions of the FPD contained comparable amounts of lag signals. When the estimated signal from the blocked regions was subtracted from the unblocked signal during scatter correction, the lag effects were corrected to a certain extent. The contrast between left and right was reduced considerably and the radar artifact became almost invisible [Figs. 10(c), 10(d), 10(h), 10(i)].
Compared to results obtained by the moving blocker method, images reconstructed by Varian appear to be smoother (Fig. 10) with more accurate HU numbers in several ROIs (Table 2), but has lower overall HU in the uniform region (Fig. 11). These differences may be attributed to additional pre‐ and post‐processing steps employed by Varian clinical scanners, such as analytical beam hardening correction based on models of the beam spectrum, additional noise suppression technique and ring artifacts correction of the final images.14, 60, 61 These processing steps were not included in our current reconstruction. By incorporating these steps, the accuracy of HU numbers can be further improved in images reconstructed with the moving blocker technique. Moreover, since part of the X‐ray beam were blocked in our method, for example, 25% X‐ray beam were blocked if we use a blocker with interspace three times of the strip width, we can increase the mAs by 25% to reduce image noise while keep the imaging dose the same as a standard scan. The Varian kernel‐based method does not provide such a possibility for noise reduction without increasing patient dose.
The use of a moving blocker system for scatter correction in CBCT reconstruction is effective to a certain range of the blocker geometric design. Image reconstruction accuracy is affected more by blocker geometry design than moving speed. Based on the realistic experimental results, the optimal geometry of the blocker has a strip width of 20 pixels (3.2 mm) and an interspace three times the strip width, corresponding to 25% detector being covered by lead strips. The optimal moving speed is 15 pixels per projection.
Conflict of interest
The authors have no relevant conflicts of interest to disclose.
Supporting information
Video S1: Moving blocker system in CBCT.
Acknowledgments
This work was supported in part by the Cancer Prevention and Research Institute of Texas (RP130109), the American Cancer Society (RSG‐13‐326‐01‐CCE), US National Institutes of Health (R01 EB020366) and the National Natural Science Foundation of China (61401349).The authors thank Dr. Damiana Chiavolini for editing the manuscript. The authors also thank Mr. Jun Fu for his help on making protection circuit for the motor.
References
- 1. Jaffray DA, Siewerdsen JH, Wong JW, Martinez AA. Flat‐panel cone‐beam computed tomography for image‐guided radiation therapy. Int J Radiat Oncol Biol Phys. 2002;53:1337–1349. [DOI] [PubMed] [Google Scholar]
- 2. Létourneau D, Wong JW, Oldham M, et al. Cone‐beam‐CT guided radiation therapy: technical implementation. Radiother Oncol. 2005;75:279–286. [DOI] [PubMed] [Google Scholar]
- 3. Xing L, Thorndyke B, Schreibmann E, et al. Overview of image‐guided radiation therapy. Med Dosim. 2006;31:91–112. [DOI] [PubMed] [Google Scholar]
- 4. Zhang Y, Yin F‐F, Segars WP, Ren L. A technique for estimating 4D‐CBCT using prior knowledge and limited‐angle projections. Med Phys. 2013;40:121701. [DOI] [PubMed] [Google Scholar]
- 5. Siewerdsen JH, Jaffray DA. Cone‐beam computed tomography with a flat‐panel imager: magnitude and effects of X‐ray scatter. Med Phys. 2001;28:220–231. [DOI] [PubMed] [Google Scholar]
- 6. Ding GX, Duggan DM, Coffey CW. Characteristics of kilovoltage X‐ray beams used for cone‐beam computed tomography in radiation therapy. Phys Med Biol. 2007;52:1595. [DOI] [PubMed] [Google Scholar]
- 7. Ding GX, Duggan DM, Coffey CW, et al. A study on adaptive IMRT treatment planning using kV cone‐beam CT. Radiother Oncol. 2007;85:116–125. [DOI] [PubMed] [Google Scholar]
- 8. Yang Y, Schreibmann E, Li T, Wang C, Xing L. Evaluation of on‐board kV cone beam CT (CBCT)‐based dose calculation. Phys Med Biol. 2007;52:685. [DOI] [PubMed] [Google Scholar]
- 9. Seibert J, Boone J. X‐ray scatter removal by deconvolution. Med Phys. 1988;15:567–575. [DOI] [PubMed] [Google Scholar]
- 10. Boone JM, Seibert JA. An analytical model of the scattered radiation distribution in diagnostic radiology. Med Phys. 1988;15:721–725. [DOI] [PubMed] [Google Scholar]
- 11. Li H, Mohan R, Zhu XR. Scatter kernel estimation with an edge‐spread function method for cone‐beam computed tomography imaging. Phys Med Biol. 2008;53:6729. [DOI] [PubMed] [Google Scholar]
- 12. Rinkel J, Gerfault L, Esteve F, Dinten J. A new method for X‐ray scatter correction: first assessment on a cone‐beam CT experimental setup. Phys Med Biol. 2007;52:4633. [DOI] [PubMed] [Google Scholar]
- 13. Spies L, Evans P, Partridge M, Hansen V, Bortfeld T. Direct measurement and analytical modeling of scatter in portal imaging. Med Phys. 2000;27:462–471. [DOI] [PubMed] [Google Scholar]
- 14. Sun M, Star‐Lack J. Improved scatter correction using adaptive scatter kernel superposition. Phys Med Biol. 2010;55:6695–6720. [DOI] [PubMed] [Google Scholar]
- 15. Ohnesorge B, Flohr T, Klingenbeck‐Regn K. Efficient object scatter correction algorithm for third and fourth generation CT scanners. Eur Radiol. 1999;9:563–569. [DOI] [PubMed] [Google Scholar]
- 16. Grimmer R, Kachelrieß M. Empirical binary tomography calibration (EBTC) for the precorrection of beam hardening and scatter for flat panel CT. Med Phys. 2011;38:2233–2240. [DOI] [PubMed] [Google Scholar]
- 17. Sun M, Maslowski A, Davis I, Wareing T, Failla G, Star‐Lack J. Rapid scatter estimation for CBCT using the Boltzmann transport equation. In SPIE Medical Imaging (International Society for Optics and Photonics), 2014;90330Z–90339.
- 18. Boone JM, Seibert JA. Monte Carlo simulation of the scattered radiation distribution in diagnostic radiology. Med Phys. 1988;15:713–720. [DOI] [PubMed] [Google Scholar]
- 19. Jarry G, Graham SA, Moseley DJ, Jaffray DJ, Siewerdsen JH, Verhaegen F. Characterization of scattered radiation in kV CBCT images using Monte Carlo simulations. Med Phys. 2006;33:4320–4329. [DOI] [PubMed] [Google Scholar]
- 20. Zbijewski W, Beekman FJ. Efficient Monte Carlo based scatter artifact reduction in cone‐beam micro‐CT. IEEE Trans Med Imaging. 2006;25:817–827. [DOI] [PubMed] [Google Scholar]
- 21. Xu Y, Bai T, Yan H, et al. A practical cone‐beam CT scatter correction method with optimized Monte Carlo simulations for image‐guided radiation therapy. Phys Med Biol. 2015;60:3567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Bootsma G, Verhaegen F, Jaffray D. Efficient scatter distribution estimation and correction in CBCT using concurrent Monte Carlo fitting. Med Phys. 2015;42:54–68. [DOI] [PubMed] [Google Scholar]
- 23. Baer M, Kachelrieß M. Hybrid scatter correction for CT imaging. Phys Med Biol. 2012;57:6849. [DOI] [PubMed] [Google Scholar]
- 24. Zhu L, Xie Y, Wang J, Xing L. Scatter correction for cone‐beam CT in radiation therapy. Med Phys. 2009;36:2258–2268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Ning R, Tang X, Conover D. X‐ray scatter correction algorithm for cone beam CT imaging. Med Phys. 2004;31:1195–1202. [DOI] [PubMed] [Google Scholar]
- 26. Jin J‐Y, Ren L, Liu Q, et al. Combining scatter reduction and correction to improve image quality in cone‐beam computed tomography (CBCT). Med Phys. 2010;37:5634–5644. [DOI] [PubMed] [Google Scholar]
- 27. Niu T, Zhu L. Scatter correction for full‐fan volumetric CT using a stationary beam blocker in a single full scan. Med Phys. 2011;38:6027–6038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Lee H, Xing L, Lee R, Fahimian BP. Scatter correction in cone‐beam CT via a half beam blocker technique allowing simultaneous acquisition of scatter and image informationa). Med Phys. 2012;39:2386–2395. [DOI] [PubMed] [Google Scholar]
- 29. Siewerdsen J, Daly M, Bakhtiar B, et al. A simple, direct method for X‐ray scatter estimation and correction in digital radiography and cone‐beam CT. Med Phys. 2006;33:187–197. [DOI] [PubMed] [Google Scholar]
- 30. Meng B, Lee H, Xing L, Fahimian BP. Single‐scan patient‐specific scatter correction in computed tomography using peripheral detection of scatter and compressed sensing scatter retrieval. Med Phys. 2013; 40:011907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Zhu L, Bennett NR, Fahrig R. Scatter correction method for X‐ray CT using primary modulation: theory and preliminary results. IEEE Trans Med Imaging. 2006;25:1573–1587. [DOI] [PubMed] [Google Scholar]
- 32. Gao H, Fahrig R, Bennett NR, Sun M, Star‐Lack J, Zhu L. Scatter correction method for X‐ray CT using primary modulation: phantom studies. Med Phys. 2010;37:934–946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Gao H, Zhu L, Fahrig R. Modulator design for X‐ray scatter correction using primary modulation: material selection. Med Phys. 2010;37:4029–4037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Gao H, Zhu L, Fahrig R. Optimization of system parameters for modulator design in X‐ray scatter correction using primary modulation. In SPIE Medical Imaging (International Society for Optics and Photonics), 2010;76222A‐76229.
- 35. Ritschl L, Fahrig R, Knaup M, Maier J, Kachelrieß M. Robust primary modulation‐based scatter estimation for cone‐beam CT. Med Phys. 2015;42:469–478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Bier B, Muller K, Berger M, et al. Scatter correction for C‐Arm CT using primary modulation. In Proceedings of the 4th International Conference on Image Formation in X‐ray Computed Tomography (CT‐Meeting 2016). Bamberg, Germany: 2016;383–386. [Google Scholar]
- 37. Zhu L. Local filtration based scatter correction for cone‐beam CT using primary modulation. Medl Phys. 2016;43:6199–6209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Zhu L, Strobel N, Fahrig R. X‐ray scatter correction for cone‐beam CT using moving blocker array. In Medical imaging 2005 (International Society for Optics and Photonics), 2005;251–258.
- 39. Liu X, Shaw CC, Wang T, Chen L, Altunbas MC, Kappadath SC. An accurate scatter measurement and correction technique for cone beam breast CT imaging using scanning sampled measurement (SSM) technique. In Medical Imaging 2006 (International Society for Optics and Photonics), 2006;614234. [DOI] [PMC free article] [PubMed]
- 40. Yan H, Mou X, Tang S, Xu Q, Zankl M. Projection correlation based view interpolation for cone beam CT: primary fluence restoration in scatter measurement with a moving beam stop array. Phys Med Biol. 2010;55:6353. [DOI] [PubMed] [Google Scholar]
- 41. Hsieh S. Estimating scatter in cone beam CT with striped ratio grids: a preliminary investigation. Med Phys. 2016;43:5084–5092. [DOI] [PubMed] [Google Scholar]
- 42. Wang J, Mao W, Solberg T. Scatter correction for cone‐beam computed tomography using moving blocker strips: a preliminary study. Med Phys. 2010;37:5792–5800. [DOI] [PubMed] [Google Scholar]
- 43. Ouyang L, Song K, Wang J. A moving blocker system for cone‐beam computed tomography scatter correction. Med Phys. 2013;40:071903. [DOI] [PubMed] [Google Scholar]
- 44. Hälg RA, Besserer J, Schneider U. Systematic measurements of whole‐body imaging dose distributions in image‐guided radiation therapy. Med Phys. 2012;39:7650–7661. [DOI] [PubMed] [Google Scholar]
- 45. Jia X, Yan H, Cerviño L, Folkerts M, Jiang SB. A GPU tool for efficient, accurate, and realistic simulation of cone beam CT projections. Med Phys. 2012;39:7368–7378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Kawrakow I. Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version. Med Phys. 2000;27:485–498. [DOI] [PubMed] [Google Scholar]
- 47. Montanari D, Scolari E, Silvestri C, et al. Comprehensive evaluations of cone‐beam CT dose in image‐guided radiation therapy via GPU‐based Monte Carlo simulations. Phys Med Biol. 2014;59:1239. [DOI] [PubMed] [Google Scholar]
- 48. Siddon RL. Fast calculation of the exact radiological path for a three‐dimensional CT array. Med Phys. 1985;12:252–255. [DOI] [PubMed] [Google Scholar]
- 49. Jacobs F, Sundermann E, De Sutter B, Christiaens M, Lemahieu I. A fast algorithm to calculate the exact radiological path through a pixel or voxel space. J Comput Info Technol. 1998;6:89–94. [Google Scholar]
- 50. Han G, Liang Z, You J. A fast ray‐tracing technique for TCT and ECT studies. In Nuclear Science Symposium, 1999, Seattle, WA: IEEE; 1999;1515–1518. [Google Scholar]
- 51. Wang J, Li T, Lu H, Liang Z. Penalized weighted least‐squares approach to sinogram noise reduction and image reconstruction for low‐dose X‐ray computed tomography. IEEE Trans Med Imaging. 2006;25:1272–1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. La Riviere PJ. Penalized‐likelihood sinogram smoothing for low‐dose CT. Med Phys. 2005;32:1676–1683. [DOI] [PubMed] [Google Scholar]
- 53. Sidky EY, Kao C‐M, Pan X. Accurate image reconstruction from few‐views and limited‐angle data in divergent‐beam CT. J Xray Sci Technol. 2006;14:119–139. [Google Scholar]
- 54. Sidky EY, Pan X. Image reconstruction in circular cone‐beam computed tomography by constrained, total‐variation minimization. Phys Med Biol. 2008;53:4777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Yu H, Wang G. Compressed sensing based interior tomography. Phys Med Biol. 2009;54:2791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Zhu L, Wang J, Xing L. Noise suppression in scatter correction for cone‐beam CT. Med Phys. 2009;36:741–752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Siewerdsen J, Jaffray D. Cone‐beam computed tomography with a flat‐panel imager: effects of image lag. Med Phys. 1999;26:2635–2647. [DOI] [PubMed] [Google Scholar]
- 58. Stankovic U, Ploeger LS, Sonke J‐J, Van Herk M. Clinical introduction of image lag correction for a cone beam CT system. Med Phys. 2016;43:1057–1064. [DOI] [PubMed] [Google Scholar]
- 59. Ren L, Yin F‐F, Chetty IJ, Jaffray DA, Jin J‐Y. Feasibility study of a synchronized‐moving‐grid (SMOG) system to improve image quality in cone‐beam computed tomography (CBCT). Med Phys. 2012;39:5099–5110. [DOI] [PubMed] [Google Scholar]
- 60. Star‐Lack J, Sun M, Kaestner A, et al. Efficient scatter correction using asymmetric kernels. In SPIE Medical Imaging (International Society for Optics and Photonics), 2009;72581Z–72512.
- 61. Star‐Lack J, Starman J, Munro P, et al. SU‐FF‐I‐04: a fast variable‐intensity ring suppression algorithm. Med Phys. 2006;33:1997–1997. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Video S1: Moving blocker system in CBCT.


