Magnesium isotope evidence that accretional vapour loss shapes planetary compositions

Abstract

It has long been recognised that Earth and other differentiated planetary bodies are chemically fractionated compared to primitive, chondritic meteorites and by inference the primordial disk from which they formed. An important question has been whether the notable volatile depletions of planetary bodies are a consequence of accretion¹, or inherited from prior nebular fractionation². The isotopic compositions of the main constituents of planetary bodies can contribute to this debate^3–6. Using a new analytical approach to address key issues of accuracy inherent in conventional methods, we show that all differentiated bodies have isotopically heavier magnesium compositions than chondritic meteorites. We argue that possible magnesium isotope fractionation during condensation of the solar nebula, core formation and silicate differentiation cannot explain these observations. However, isotopic fractionation between liquid and vapour followed by vapour escape during accretionary growth of planetesimals generates appropriate residual compositions. Our modelling implies that the isotopic compositions of Mg, Si and Fe and the relative abundances of the major elements of Earth, and other planetary bodies, are a natural consequence of substantial (~40% by mass) vapour loss from growing planetesimals by this mechanism.

Magnesium is a fundamental building block of the terrestrial planets, constituting ~15% of Earth’s mass. Compared to the ‘solar’ composition of the primordial disk, it is well established that the Earth is depleted in Mg by ~20% relative to more cosmochemically refractory elements (e.g. Al), consistent with increasing terrestrial depletions of elements with higher volatility (e.g. ref [7]). Mass-dependent isotopic fractionations of other major elements, Si and Fe, have been used to argue for compositional modification by accretional vapour loss^3,6. Yet contrasting conclusions have been derived from similar observations in studies that point to fractionations occurring for these elements during planetary differentiation^8,9. In this respect, the isotopic composition of Mg may be better suited to interrogate chemical fractionation in the Solar System⁵. However, detecting mass-dependent isotopic differences between primitive chondrites and differentiated bodies poses significant analytical challenges because only small (<<1‰/amu) fractionations typically occur during the high temperature processes (>1300 K) that shape planetary evolution. Indeed, various comparisons of terrestrial and chondritic Mg isotope ratios have reached opposing conclusions as to whether or not the Earth is chondritic^5,10–17. Much of the divergent opinion appears to stem from difficulties in achieving sufficiently accurate measurements¹⁸.

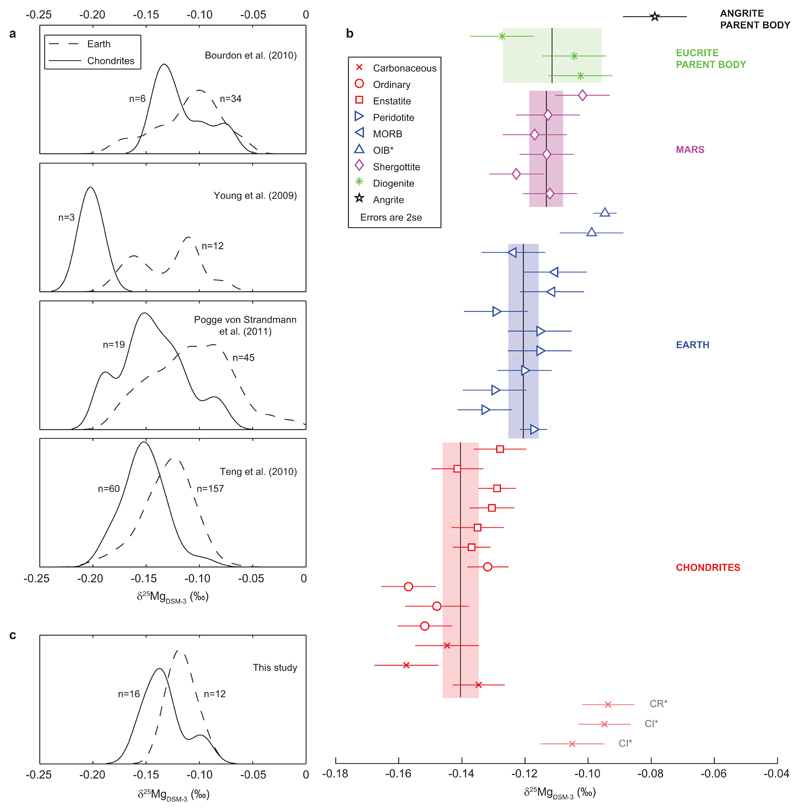
In Figure 1a we illustrate that a number of different studies report chondritic ²⁵Mg/²⁴Mg ~0.03-0.05‰ lower than the Earth^5,10–12, but in only one case do the authors actually argue that the Earth is non-chondritic⁵. Reliable resolution of such small isotopic differences requires tight control on analytical artefacts. Of particular concern is that samples and standards behave slightly differently during analysis, despite prior purification. Unlike the traditional sample-standard bracketing approach, the method of double-spiking explicitly corrects such behaviour, but it is not standard for elements with only three stable isotopes, like magnesium. We have, therefore, developed a new approach of “critical mixture double spiking” to overcome this problem¹⁹ (see Methods for details). Based on propagation of conservative estimates of systematic error, this method has a limiting accuracy <0.005‰/amu¹⁹. Repeat measurements of solution standards and geological reference materials indicate that we can achieve reproducibilities of ±0.010‰ (2se) for octuple measurements.

Figure 1.

Magnesium isotope compositions. a) Probability density plots of Mg isotope compositions from previous standard-sample bracketing work, highlighting the results of individual studies⁵,¹⁰–¹² that presented numerous analyses of both terrestrial and chondritic samples using the same methodology. These data show systematic subtle differences (0.02-0.05‰) between the Earth and primitive meteorites. Typically authors refrained from interpreting such small differences. b) Samples from this study (measured by critical mixture double spiking) ordered according to sample-type. Lines and shaded bars indicate means and 2se. Samples displayed with pale symbols are excluded from means (see main text). c) Earth and chondrite analyses from b) shown as probability plot to compare with a).

We have measured the Mg isotope compositions of a range of terrestrial rocks and primitive and differentiated meteorites using critical mixture double spiking (Table 1). As shown in Figure 1b,c, our new data substantiate that chondrites have ²⁵Mg/²⁴Mg ~0.02‰ lower than the differentiated Earth, Mars, eucrite and angrite parent bodies.

Table 1.

Magnesium isotope compositions of chondrites, terrestrial (ultra-)mafics, and achondrites.

Sample	Type	δ25Mg (‰)	2se	n1
Orgueil	CI1	-0.105	0.010	8
Ivuna	CI1	-0.095	0.008	12
Al Rais	CR2	-0.094	0.008	12
Renazzo	CR2	-0.135	0.008	12
Kainsaz	CO3	-0.158	0.010	8
Murchison	CM2	-0.145	0.010	8
Parnallee	LL3	-0.152	0.009	11
Dhurmsala	LL6	-0.148	0.010	8
Ceniceros	H3	-0.157	0.009	11
Zag	H3	-0.132	0.007	19,2
Khairpur	EL6	-0.137	0.006	23,2
Hvittis	EL6	-0.135	0.008	12
Yilmia	EL6	-0.130	0.007	16
St Mark's	EH5	-0.129	0.006	23,2
Abee	EH4	-0.142	0.008	12
Indarch	EH4	-0.128	0.008	12
Mean Chondrites2		-0.140	0.006
JP-1	Dunite	-0.117	0.004	43,5
BZ116	Sp Hz	-0.133	0.009	11
Vi 313-102	Gt Lz	-0.130	0.010	8
BZ143	Sp Lz	-0.120	0.009	11
BZ-29	Sp Lz	-0.115	0.010	8
Vi 314-56	Sp Lz	-0.115	0.010	8
BZ251	Plg Lz	-0.129	0.010	8
2370-1	MORB	-0.111	0.010	8
DS12-29	MORB	-0.110	0.010	8
9/30a(1)	MORB	-0.124	0.010	8
BIR-1	OIB	-0.099	0.010	8
BHVO-2	OIB	-0.095	0.004	60,3
Mean Earth3		-0.121	0.005
ALHA 77005	Lz Sherg	-0.112	0.009	11
DaG 476	Bas Sherg	-0.123	0.009	11
EETA 79001	Bas Sherg	-0.113	0.009	11
RBT 04262	Ol Sherg	-0.117	0.010	8
Zagami	Bas Sherg	-0.113	0.010	8
LAR 06319	Ol Sherg	-0.102	0.009	11
Mean Mars		-0.113	0.006
Johnstown	Diogenite	-0.102	0.010	8
Shalka	Diogenite	-0.104	0.010	8
Tatahouine	Diogenite	-0.127	0.010	8
Mean Diogenites		-0.111	0.016
d'Orbigny	Angrite	-0.079	0.010	8

¹Total number of analyses. If a comma is present, the number behind the comma refers to the number of digestions. Each digestion was passed through chemistry once.

²The two CI1 chondrites (Ivuna, Orgueil) and one CR2 (Al Rais) were excluded from the mean.

³The two Ocean Island Basalts (BHVO-2 and BIR-1) were excluded from the mean.

Sp Hz = Spinel Harzburgite, Gt Lz = Garnet Lherzolite, Plg = Plagioclase, MORB = Mid-Ocean Ridge Basalt, OIB = Ocean Island basalt, Bas Sherg = Basaltic Shergottite, Ol = Olivine-phyric.

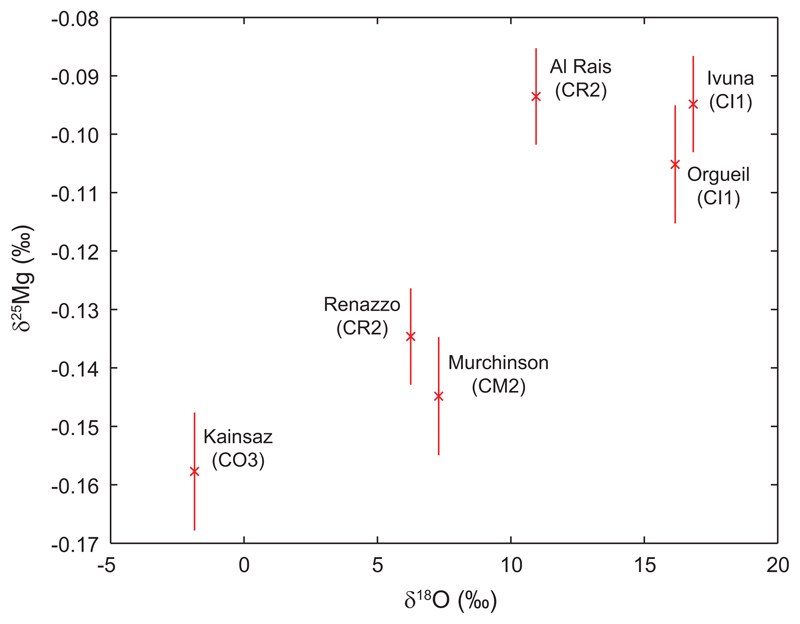
Visual (Figure 1b) and statistical (see Methods) inspection shows some data scatter. For terrestrial samples this is mostly due to two ocean island basalts (OIB), whose sources likely contain recycled components, originally fractionated at Earth’s surface. However, we focus on analyses of mantle peridotites to estimate the composition of bulk Earth more robustly. Mg isotope variability among chondrites is foremost within the carbonaceous group. This scatter is readily explained by variable parent body aqueous alteration, as their ²⁵Mg/²⁴Mg vary systematically with oxygen isotope compositions²⁰ and petrographic class (Extended Data Figure 1) in the sense anticipated from terrestrial weathering²¹. Removing these anomalous samples, we document a statistically significant difference in Mg isotope compositions between chondrites and the variably-sized, differentiated bodies of Earth, Mars and the eucrite parent body (p_ANOVA 1.5×10^-6). If enstatite chondrites are considered separately from other chondrites (p_t-test 0.017), their mean ²⁵Mg/²⁴Mg is also significantly lighter than differentiated bodies (~0.013‰; p_ANOVA 7.8×10^-4). In contrast, the differentiated bodies are statistically indistinguishable from each other (p_ANOVA 0.16).

The lack of systematic differences in ²⁵Mg/²⁴Mg between melt-depleted harzburgites, fertile lherzolites and mid-ocean ridge basalts reaffirm, at higher precision, previous observations¹² that Mg isotopes do not fractionate discernibly during (ultra)mafic silicate differentiation (Figure 1, Table 1 and Extended Data Figure 2). Silicate differentiation is, therefore, not responsible for the relatively heavy Mg isotope compositions of our samples of differentiated planetary bodies.

Although the difference in ²⁵Mg/²⁴Mg between Earth and primitive meteorites is small, bulk perturbation of such an abundant element requires the operation of planetary scale processes. Core formation cannot account for this observation, because unlike Fe and Si, Mg only becomes siderophile at temperatures too high for significant isotopic fractionation²². Vapour fractionation typically produces larger isotopic differences than magmatic processes. Such fractionation may have occurred during initial condensation of solids from the cooling proto-solar nebula, as has been invoked to explain variability between meteoritic and planetary silicon isotope compositions⁴. Yet, such a model predicts the low Mg/Si enstatite chondrites should have the lowest ²⁵Mg/²⁴Mg of the primitive meteorites. This is inconsistent with our observations, in which enstatite chondrites have the isotopically heaviest Mg of the anhydrous chondrites and the Earth, moreover, is distinct from chondrites.

Instead, we propose that differentiated planetary bodies obtained their relatively heavy Mg isotope compositions by vapour-melt fractionation following impacts during accretionary growth of planetesimals. Loss of vapour, which was subsequently swept into the Sun or blown beyond the zone of accretion, would leave residual planetary bodies isotopically heavy. Vapour loss is most effective for bodies <~0.1 Earth masses (M_⊕) as escape velocities of larger bodies are mostly too high to be exceeded by silicate vapour molecules (see Supplementary Information). We posit that vapour loss signatures were abundantly imparted to small bodies in the inner Solar System, as evidenced by our analyses of silicate achondrites (Figure 1b). Larger bodies like Earth dominantly accreted from such vapour depleted planetesimals, thereby inheriting their signatures.

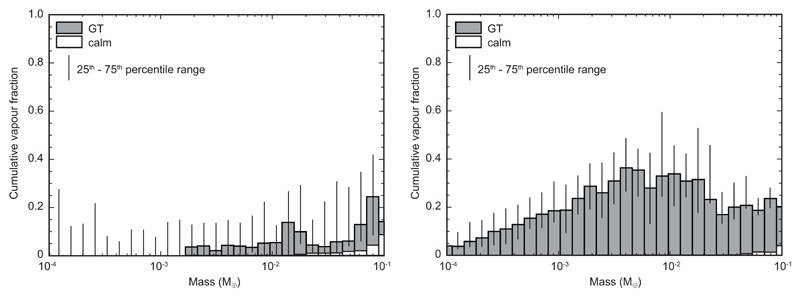
Although small bodies can readily lose vapour, low mutual impact velocities limit the amount of vapour produced directly during these early stages of accretion. To investigate this quantitatively, we have post-processed the results of previously published, high-resolution N-body simulations²³ (see Methods for details) using a parameterisation of impact-induced vaporisation⁴. In this model, cumulative vapour produced increases from <1 to ~20% of a body’s final mass for bodies from 10^-4 to 10^-1 M_⊕ (Figure 2a). As an alternative approach we have calculated vapour mass loss by direct outflow of silicate vapour from the surface of impact-generated magma ponds/oceans (see Supplementary Information for details). Although magma oceans may have been produced by radiogenic heating (e.g. ²⁶Al decay), we conservatively focussed on converting impact velocities of the same N-body simulations to energy available for melting/vapour outflow. We obtain cumulative vapour mass losses of ~4-36% for bodies with 10^-4 to 10^-1 M_⊕ final masses (Figure 2b). Given the higher mass losses from smaller bodies in the second, magmatic scenario we focus on this process.

Figure 2.

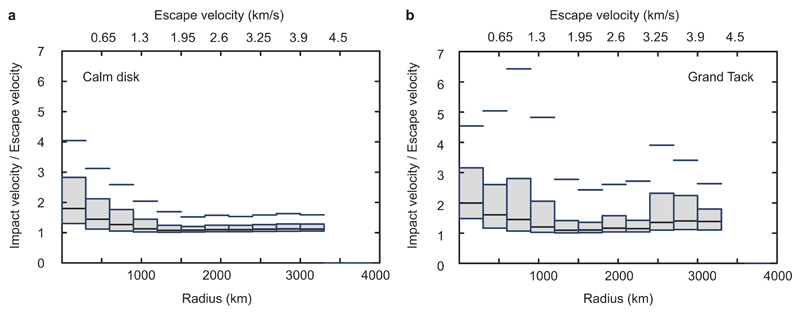
Median cumulative vapour fractions produced as a function of final planetary mass (in Earth masses M_⊕) determined from high-resolution N-body simulations of planetary accretion²³. The N-body simulations encompassed two scenarios: a calm disk without gas drag (“calm”) and a disk that is disturbed by a Grand Tack motion of Jupiter³⁰ (“GT”). a) Vapour loss fractions calculated for impact vaporisation parameterised to impact velocity⁴. b) Vapour loss fractions produced by direct outflow above exposed magma ponds/oceans. In a Grand Tack scenario, Jupiter’s motions cause higher eccentricities and hence higher impact velocities for such small bodies, which explains their high vapour fractions.

The outflow velocities of vapour above the magma ponds/oceans are sufficiently high that this mechanism is not mass discriminative. This implies that isotopic fractionation only occurs during production of vapour at the surface of the magma pond/ocean. We treat this as an equilibrium process between a molten surface and transient atmosphere, as vapour-liquid chemical equilibrium is attained rapidly²⁴. Furthermore, kinetic isotope fractionation in this scenario can be ruled out empirically from consideration of marked effects on K isotope ratios that are unobserved in nature²⁵ (see Methods).

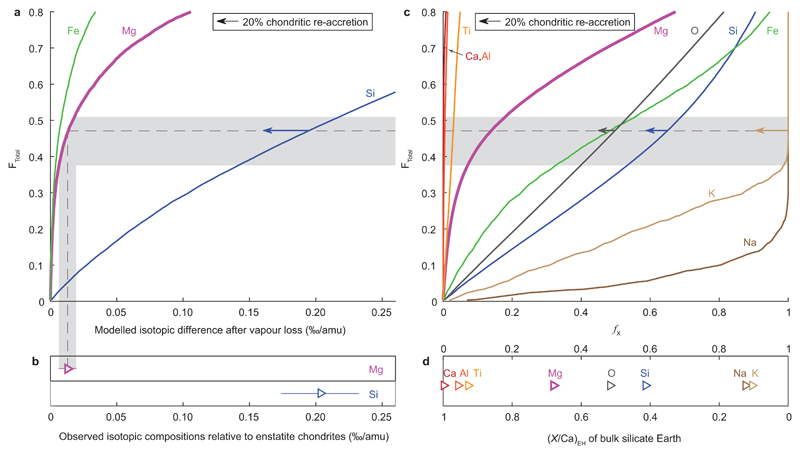
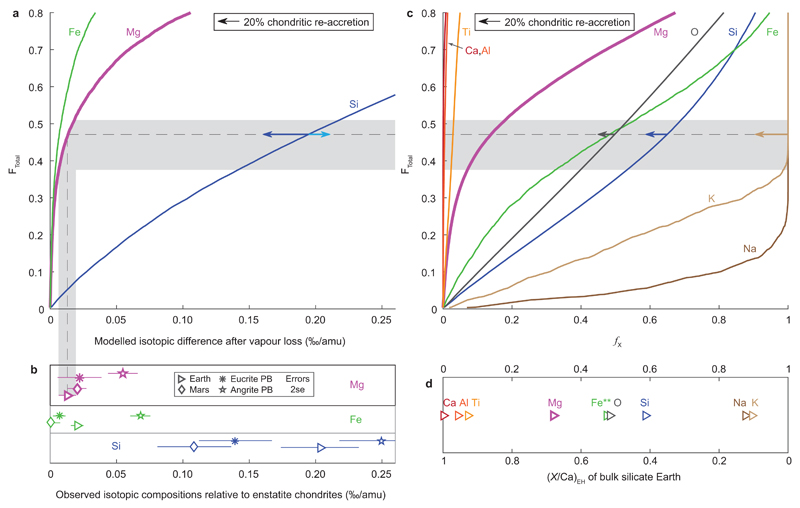
We have modelled Mg, Si and Fe equilibrium isotope fractionation between a liquid and vapour with compositions calculated using thermodynamic data for a nine-component system of major and minor elements of variable volatility (see Methods for details). To obtain a residual planetesimal with a Mg isotope composition ~0.02‰ higher than our average chondritic value, our model predicts ~0.30‰ and ~0.013‰ super-chondritic ³⁰Si/²⁸Si and ⁵⁶Fe/⁵⁴Fe (Figure 3a). These values are largely compatible with the Earth (Figure 3) and several other bodies (Extended Data Figure 3), despite some currently rather poorly constrained input parameters (see Methods); refinement of these values may resolve these minor mismatches. Starting more specifically with an enstatite chondrite composition, as thought most isotopically appropriate for Earth (e.g. ref [26]), ~47% of the body is vaporised and lost, which removes ~14% of the initial Mg mass together with ~65% Si, ~48% Fe and >99.9% of Na and K (Figure 3c). Similar total mass losses were deduced previously for Earth²⁷ from the volatilities of major constituents based on a comparison to vaporisation experiments. The total mass losses inferred from these chemical constraints (Figure 3) are reassuringly similar to those calculated from our physical model of vapour loss (Figure 2b).

Figure 3.

Comparison between modelled compositions of a vapour depleted liquid and observed terrestrial compositions. a) Changes in isotope compositions (‰/amu) against total relative vapour loss (F_Total, in mole fractions) calculated in our model. b) Observed terrestrial Mg (this study), and Si (from [4] and references therein) isotope compositions relative to enstatite chondrites (EH). Errors are 2se. c) Loss (mole fraction) of a given element (X), f_X, versus F_Total. d) Molar element/Ca of the terrestrial mantle⁷, normalised to EH³¹. Shaded bands give error bounds for F_Total inferred from Mg isotope data and the intersection of different curves with this field indicates the range of terrestrial depletions predicted for our vapour loss model. Comparison of these values to those calculated for the Earth relative to an enstatite chondrite starting composition (b and d) is generally good, despite uncertainties in model input parameters (see Methods) and additional influences on observed values from nebular and core formation processes⁴,⁹. Left pointing arrows show the effect of post-volatile loss accretion of 20% chondrite (EH).

The predicted elemental losses modify the composition of enstatite chondrites into one similar to the Earth’s (Figure 3c,d), without requiring substantial, preferential collisional erosion of a putative crust formed by small degrees melts of an undifferentiated body²⁸. Our modelled vapour-loss modification resolves the conundrum that Earth’s isotopic anomalies suggest a close genetic link to enstatite chondrites despite vastly different elemental compositions²⁶. Close matches to Earth’s composition are also obtained, however, when starting with e.g. a CI chondrite composition (Extended Data Figure 4). While potassium depletion relative to chondrites in eucrite (>94%) and angrite (>99%) parent bodies²⁵ is comparable to our vapour depletion model results, it requires re-accretion of ~20% chondritic material to match terrestrial alkali abundances. This material can be derived from the distribution tail of bodies that escape melting and vapour loss.

Our vapour loss model quantitatively accounts for non-chondritic abundances and isotopic compositions of major elements as a natural consequence of planetary accretion and provides a viable mechanism for previous suggestions of the importance of evaporative losses in planetary evolution^3,6,27,29. This process inevitably results in dramatic loss of elements more volatile than Mg. Planetary compositions thus intrinsically reflect their history of collisional formation.

Methods

Chemical and analytical protocols, and data statistics

Powdered samples were digested in cleaned Savillex PFA beakers with 3:1 ultra-pure ~15.5M HNO₃ and ~28M HF. Prior to drying, ~0.5 ml 7M HClO₄ was added to prevent precipitation of insoluble fluorides. At this stage, insoluble chromites were visible in some peridotites. They were separated from the supernatant and further digested in high-pressure acid digestion vessels (Anton Paar Asher) before being re-combined with the rest of the digested sample. Similarly, graphite precipitates were removed from enstatite chondrites by transferring the samples into pre-cleaned BN crucibles that were placed in a muffle furnace at 600 °C, making use of the phase transition of graphite to CO₂ under these conditions. Following complete digestion, any remaining organic components were attacked with ~15.5M HNO₃ and 30% H₂O₂. Terrestrial samples generally weighed 2-15 mg, while larger meteorite samples were dissolved (~7-150 mg, majority 60-100 mg; see Extended Data Table 1) to obtain representative samples.

Magnesium was separated from the sample matrix with a Biorad AG50W-X12 cationic exchange resin and 2M HNO₃ eluent as described previously¹¹. Yields were monitored and were >99.85% for all analysed samples. Following separation, samples were dissolved in 0.3M HNO₃ and critically double spiked (see below) for analyses on a Thermo Finnigan Neptune (s/n 1020) multi-collector inductively coupled plasma mass spectrometer (MC-ICPMS). A Savillex PFA nebuliser (30-40 μl min^-1 uptake) aspirated the sample solution into an Elemental Scientific Inc. Apex HF introduction system prior to ionisation in the plasma. A combination of Jet sampler and H skimmer cones was used and Mg masses 24, 25 and 26 were collected in cups L4, centre and H4, respectively. The Neptune was further operated in medium resolution mode (M/ΔM ≥ 4000, 5-95% peak height definition) with an off-peak centre mass (²⁵Mg mass 24.979 instead of 24.986) to resolve any minor possible ¹²C¹⁴N⁺ interferences on ²⁶Mg⁺. However, these interferences should be insignificant as they were observed to be only ~15 ppm of the ²⁶Mg⁺ signal. This medium resolution mode also improved signal-to-noise ratios, reducing total background signals to <2×10^-13 A. A 10¹¹ Ω feedback resistor was used in the amplifier connected to the centre cup, while 10¹⁰ Ω resistors were used on L4 and H4. Total Mg intensities of ~2×10^-9 A were measured at total Mg concentrations of ~2.5 µg ml^-1 for 168 s integration (20 cycles of 8.4 s), consuming ~185 ng sample Mg per analysis in double-spiked samples.

A measurement sequence typically consisted of analysis of a mixture of double spike and DSM-3 reference standard followed by three sample – double-spike mixtures, repeating until all samples were measured before starting this series again to make duplicate analyses of samples. Normally, double-spike – sample mixture measurements were repeated four times per sequence, in which a total of 9-17 samples were measured. Sequences were repeated in different analysis sessions over the course of the study to yield at least 8 repeated analyses of each double-spike – sample mixture. All sample and standard analyses were preceded by a 240 s wash-out and an on-peak background measurement (168 s integration). The mean intensities of the latter were subtracted from the intensities of the sample or standard analysis that followed it. Additionally, three analyses of unspiked DSM-3 (the concentration matched to the double-spike – sample mixtures) were performed before, after and in the middle of the sequence of double-spike – sample (or standard) mixtures. A 15 minute wash-out was performed between these unspiked and spiked analyses because the Mg isotope composition of the background greatly changes as a consequence of switching between spiked and unspiked analyses, which makes critical mixture double spiking more prone to added variability due to background corrections. In our analyses, background corrections usually affected the reported isotope compositions by <0.0005‰, which is well below the uncertainties of 0.008-0.010‰. Sequences typically took ~10-20 hours.

Interferences by hydrides (i.e. ²⁴MgH⁺ on ²⁵Mg⁺ and ²⁵MgH⁺ on ²⁶Mg⁺), which are difficult to fully resolve, as well background Mg intensities were reduced by using a -1 kV extraction voltage instead of the default -2 kV. We observed that such a change in the extraction voltage reduces background ²⁴MgH⁺ and ²⁵MgH⁺ intensities by ~10 times, i.e. ~500 cps ²⁴MgH⁺ in medium resolution. Simultaneously, the change in extraction voltage lowers background Mg intensities by ~4-5 times, while sample sensitivity is only reduced by <20%. Applying an extraction weaker than -1 kV further decreases backgrounds, but increasingly lowers sensitivity. We interpret these effects as evidence that the background signals are dominantly produced by liberation (with/without hydride) of Mg deposited at the back of the skimmer cone. This hypothesis is substantiated by the fact that progressively increasing Mg background intensities can be lowered by brief cleaning of the back of the skimmer cone with a droplet of dilute HNO₃. Moreover, background Mg isotope compositions are extremely light after mass bias correction with the same instrumental fractionation factor as for sample Mg, suggesting additional mass fractionation. Finally, we observed that hydride intensities increase over background only ~75 fold when Mg intensities are increased ~25’000 fold by introducing sample Mg. We thus estimate that the largest relative hydride intensity contribution to Mg (²⁴MgH⁺/²⁵Mg⁺) is ~13 ppm. Since we externally normalise samples to intensity matched DSM-3 standards (see Critical mixture double spiking below), these hydride contributions are reduced to such small levels that they do not affect our reported isotope compositions.

Data in Table 1 are reported as relative differences of isotope ratios to the reference solution standard DSM-3³² in delta notation following IUPAC recommendations³³: ${\delta }^{25/24}Mg=\left({\left({}^{25}Mg/{}^{24}Mg\right)}_{Sample}/{\left({}^{25}Mg/{}^{24}Mg\right)}_{DSM-3}-1\right).$ The data are presented in per mil and represent means of repeated analyses. Reported uncertainties are standard error of the mean (2se) calculated as 2s/√n in which n is the number of repeated analyses for the corresponding sample. Instead of using the standard deviation (s) of a geological reference material (e.g. BHVO-2, 2s = 0.029‰, n = 60 from 3 digestions), we determined s by a homoscedastic approach, pooling over all standards and samples³⁴. That is, after determining the sums of the squared deviations of n repeated measurements from their m sample (and standard) means, these sums were themselves summed before dividing by the degrees of freedom (k): $s^2=\frac{1}{k}{{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^{n_i}\left(x_{ij}-{\overline{x}}_i\right)}}}^2$ with $k=\left({\displaystyle \sum _{i=1}^m{n}_i}\right)-m.$ We obtained 2s = 0.029‰ (k = 693) and have found justification in using this scheme because the n repeats of m samples and standards passed the null hypothesis of a Bartlett’s test, i.e. the m samples and standards come from normal distributions with the same variance.

Group means (e.g. Earth) and their 2se uncertainties are calculated directly from the relevant sample data in Table 1. Significances of group mean differences were determined with a one-way Analysis of Variance (one-way ANOVA) or a two sample Student’s t-test, again using the relevant data in Table 1. Within group differences were investigated with one-way ANOVA using sample repeat measurements.

Critical mixture double spiking

The analysis routine described above is broadly similar to previous studies performed by standard-sample bracketing. Our contribution to addressing previously observed inter-laboratory inconsistencies¹⁸ resides in the novelty of adding a double-spike prior to mass-spectrometric analysis. As detailed elsewhere¹⁹, this technique of “critical mixture double spiking” corrects for mass bias effects of residual matrix, eliminating the most plausible cause for the inter-laboratory inconsistencies. It helps ensure that analyses are not only precise, but also accurate to within the quoted precision. In practice, we dissolved ²⁵MgO and ²⁶MgO spikes (purchased from Oak Ridge National Laboratory, batch numbers 217201 and 158690, respectively) and mixed them to produce a double spike with ^24,25,26Mg abundances of 0.30%, 6.27%, 93.43%, approximating those for an accuracy optimised scenario (0%, 8.4%, 91.6%, respectively¹⁹). We calibrated this double-spike to reference solution standard DSM-3 following our suggested protocol¹⁹.

After ion exchange chemistry, we aliquoted a weight of separated Mg sufficient for at least 10 runs and mixed this with a weighed amount of double-spike estimated to yield a molar spike proportion of 0.5908 in the mixture. This is the critical mixing proportion for our double-spike composition. Prior to analysis, double-spike – sample mixtures were equilibrated at 100 °C for 2-3 h in closed Savillex PFA autosampler vials. Subsequently, all samples were analysed once by MC-ICPMS in a short sequence to determine their deviation from the critical spike proportion. At this stage, the mixtures were rarely within our acceptable bound of ±0.5% molar proportion from critical. Based on the documented sample and double-spike weights and the observed double-spike proportion, either sample or double-spike was added to the mixtures, followed by another short analysis sequence. At this stage most mixtures were found to be within 0.5% from critical.

An estimate of the instrumental mass bias is required for critical mixture double spiking¹⁹. We obtained this estimate from the unspiked DSM-3 analyses in the analysis sequence by dividing the measured ^25/24Mg by the reference ^25/24Mg of 0.12663³⁵. Although this can also be done on ^26/24Mg, we find that ^25/24Mg is a more reproducible indicator of mass bias because it is less affected by incomplete wash-out due to the smaller contrast between the unspiked and spiked ratios. These instrumental mass bias factors were linearly or quadratically interpolated based on the evolution of DSM-3 – double-spike mixtures to obtain a close mass bias approximation for the sample – double-spike mixtures. Once the mass bias estimate was obtained, the analyses were run through a double-spike inversion routine, followed by a normalisation of sample isotope compositions to DSM-3 isotope compositions (obtained from double-spike – DSM-3 mixtures) to correct for residual non-exponential mass fractionation in the instrument.

Our observations are that the mass bias rarely varies by >0.5‰/amu during a 20 h sequence and that this variation tends to be characterized by a smooth evolution. Therefore, we conservatively estimate that the interpolated mass bias is accurate to ≤0.25‰/amu. Combined with our criterion of double-spike proportions being ≤0.5% from critical, we calculate that our Mg isotope compositions should be accurate to better than 0.005‰ on ²⁵Mg/²⁴Mg¹⁹. Note that this accuracy estimate is distinct from the reported uncertainty, which is determined from the scatter of replicates.

We have also analysed USGS geological reference material BHVO-2 with a deviation from a critical spike proportion of -1% (overspiked) and +1% (underspiked). The means of these samples are -0.092±0.007‰ and -0.090±0.007‰, respectively. They are hence not significantly different at this level of precision, giving further confidence that our ±0.5% mixing bound is sufficiently tight for accurate results.

Previously published data measured on key reference samples scatter beyond their 2se uncertainties¹⁸. Assuming sample homogeneity, this scatter highlights the distinction between accuracy and precision, which cannot be assessed separately in the traditional standard-sample bracketing procedure used by those studies. Whilst some of the data may thus appear precise, they can still be inaccurate. In contrast, we have assessed that our new critical double spiking technique should be accurate within our quoted precision. Hence, application of our technique should reduce the scatter in potential future studies from that observed in Extended Data Figure 5 to within the error bounds of the isotope ratios found in this study, assuming sample homogeneity. Nonetheless, much of the literature data has δ^25/24Mg consistent with our critically double spiked measurements at a ±0.25‰ level (Extended Data Figure 5).

N-body collisional accretion simulations

Our N-body collisional accretion simulations have previously been published²³ and the reader is referred to the original publication for model details. These simulations were ideally suited for our investigations because they included growth of planetary bodies from ~10^-4 to ~10^-1 M_⊕ with imperfect accretion. We used two different modes of the high resolution simulations²³, which include i) a calm disk, and ii) the Grand Tack³⁰. Whilst we did not modify the simulations in any manner, we extracted additional information (notably impact parameters) to compute accretional vapour loss by two different mechanisms.

1. Impact vaporisation

This information was obtained following published vapour fraction equations (assuming molten basalt)⁴. The equations enabled determining vapour mass (M_vap) as a fraction of the impactor mass (M_imp) in each collision. The vapour mass fraction in each collision (f_vap) was calculated from the impact velocity and angle (v_imp and θ), which we have obtained from the N-body simulations (correcting for the expanded radii that were used in these simulations to increase the collision rate): $f_{vap}=M_{vap}\left(v_{imp}\text{sin}\theta \right)/M_{imp}.$ The vapour fraction in each collision was subsequently integrated over all collisions a body experienced, taking into account that each planetesimal has its own collisional history, to obtain the fraction of material that experienced impact induced volatilisation relative to the total mass of a body: $F=\left(1/M\right){\displaystyle \underset{0}{\overset{M}{\int }}{f}_{vap}\left(v_{imp}\text{sin}\theta \right)}dm.$ This equation is modified from the original⁴ by replacing the v_esc(m) term, which was a proxy for impact velocity, by the impact velocities (v_imp) obtained in our N-body simulations. This replacement resulted in higher volatilisation fractions in our study compared to Dauphas et al.⁴, particularly for the Grand Tack simulation in which higher impact velocities occur due to dynamical excitation by Jupiter’s migration. We obtained Figure 2 by binning the results for F in groups of masses (relative to Earth’s mass M_⊕) in each of the two simulation modes.

2. Vapour mass loss by direct outflow above exposed magma ponds

Summary: The overall picture is as follows. We use the impact information from the N-body collisional accretion simulations and let each impact generate a hemispheric pool of melt. Vapour forms above the melt pool, with a pressure determined by the melt pool temperature. The melt vapour escapes at a rate determined by its temperature and the gravity of the body. The melt pool is assumed to be convecting vigorously, keeping it isothermal, and it cools from the surface due to evaporation and radiative heat transfer. As the melt cools, the vapour pressure drops and the vapour mass loss rate decreases until it effectively stops.

This overall behaviour is described by an energy equation as follows:

$$m{C}_p\dot{T}=\dot{m}\left(\frac{GM}{R_s}+L_v\right)+A\sigma T_{eff}^4$$ (1)

where the left-hand side denotes the energy source (secular cooling of the melt pool) and the right-hand side denotes the energy sinks (evaporative cooling, gravitational potential energy and radiative heat transfer). Here m is the mass of the melt pool, C_p is its specific heat capacity, Ṫ is the cooling rate of the melt pool, ṁ is the vapour mass loss rate, M is the mass of the body, R_s is its radius, G is the gravitational coefficient, L_v is the latent heat of vaporization, σ is Stefan’s constant, T_eff is the effective radiating temperature of the melt pool and A is its surface area. We take C_p =1200 Jkg^-1K^-1 , L_v=5 MJ kg^-1 and the magma density and body bulk density to both be 3000 kgm^-3.

Below we describe the different energy sources and sinks, and our calculation methods, in more detail. We have deliberately tried to keep our approach relatively simple, but even so there are a large number of parameters, some of which are highly uncertain. That being the case, a more complicated model seems premature; our main aim is to demonstrate that vapour loss from melt ponds is a plausible mechanism for generating vapour mass loss, and thereby isotopic fractionation.

Mass loss rate: Atmospheres which have a gas thermal velocity comparable to the escape velocity of the body are vulnerable to loss by direct outflow³⁶. For Earth-mass bodies the thermal velocity required is implausibly high (except perhaps for close-in “roaster” planets that may occur in exoplanetary systems³⁷) but for small bodies this requirement is less restrictive. The resulting outflow can be described by the equations of mass and momentum conservation:

$$\frac{1}{\rho }\frac{d\rho }{dr}+\frac{1}{v}\frac{dv}{dr}+\frac{2}{r}=0$$ (2)

$$\frac{1}{\rho }\frac{dP}{dr}+v\frac{dv}{dr}=-\frac{GM}{r^2}$$ (3)

where r is the radial coordinate, P(T), ρ(T) and v are the pressure, density and radial velocity of the gas and we are assuming spherical geometry. For an ideal gas we have $R\prime T=P/\rho ={v_s}^2$ where R’ is the gas constant divided by the molar mass, T is the gas temperature and v_s is the sound speed. To close the system, we also need an energy equation. The simplest, which we will adopt here, is to assume an isothermal atmosphere with the temperature set by the melt pool surface temperature T. A more realistic description would be to assume a vapour-saturated atmosphere; Lehmer et al.³⁸ have shown that this latter system is actually well-approximated by the isothermal description.

Under these assumptions, the gas will accelerate outwards until it reaches the “sonic point” at which v=v_s. At this critical radius r_c the sonic velocity is half the local escape velocity, with

$$r_c=\frac{GM}{2R\prime T}=R_s{\left(\frac{v_{esc}}{2v_s}\right)}^2$$

and v_esc is the escape velocity at the body surface (r=R_s). The atmospheric mass loss rate is then given by $4\pi {r_c}^2\rho (r_c)v_s.$ Given the surface density, equations (2) and (3) may then be integrated outwards to calculate ρ(r_c) and thus the mass loss rate. For small bodies, r_c may be equal to or less than R_s, in which case the mass loss rate is $4\pi {R_s}^2\rho (R_s)v_s.$ In our case the gas density at the surface ρ(r_s) is set by the vapour pressure of the melt pool. Because only the melt pool is losing vapour, we replace 4πR_s² with A, the melt pool area, in our mass loss calculations. We assume a molar mass of 0.04 kg/mol, appropriate for MgO or SiO.

Driving mass loss requires energy because of two effects (equation 1): conversion of liquid to vapour takes latent heat, and removal of mass from the surface to large distances involves potential energy changes. We consider both these effects in more detail below.

Secular cooling and radiative heat transfer: Secular cooling of the melt pool provides the energy to drive mass loss. The melt pool is assumed isothermal (temperature T) due to vigorous convection. This temperature sets the gas vapour pressure at the surface. Here we take the vapour pressure to be given by the following empirical expression obtained from our thermodynamic liquid-vapour model (see below):

$$\text{ln}P=-4.0041{(\text{ln}T)}^3+88.788{(\text{ln}T)}^2-639.3\text{ln}T+1480.23$$

where P is in bars.

An important aspect of our model is that the effective radiating temperature of the melt pool T_eff is lower than the temperature T which sets the gas vapour pressure and defines the internal temperature of the melt. This effect is observed at terrestrial lava lakes, where the surface temperature is typically many hundreds of K cooler³⁹ than the measured subsurface magma temperature and that inferred from the gas equilibrium chemistry⁴⁰. A similar effect is found at Io, where the majority of a lava lake’s surface is at much lower temperature than the expected magma temperature⁴¹.

The reason for this effect is that there is a thin conductive skin on top of the convecting magma, which is at a lower temperature than the material beneath. To approximately describe this phenomenon, we set the heat flux conducted across this layer equal to the heat flux radiated from the top surface:

$$F=\frac{k(T-T_{eff})}{\delta }=\sigma T_{eff}^4$$

where k is the thermal conductivity and δ is the skin thickness. This allows us to solve for T_eff given T and δ. To calculate δ we assume the convecting melt pool can be described by isoviscous convection⁴²

$$\delta \approx 2{\left(\frac{\kappa \eta }{\rho g\alpha [T-T_{eff}]}\right)}^{1/3}$$

At high temperatures, the dominant energy sink in equation (1) is evaporative cooling, because radiative heat loss increases as T⁴, while mass loss (which depends on the vapour pressure) increases exponentially with T. Thus, the overall mass loss calculations are not particularly sensitive to the details of the radiative cooling calculations.

Here we take α=3x10^-5 K^-1, η=10³ Pa s. The thermal conductivity k is taken to be 3 Wm^-1 K^-1 which then specifies κ. For T=1400 K and a 1000 km radius body we find T_eff=853 K, which is roughly consistent with terrestrial lava lake measurements³⁹.

Melt pool volume and temperature: To calculate the melt pool volume and temperature we assume that the volume of material shocked to the maximum temperature (the isobaric core) is hemispherical and has a radius linearly proportional to the impactor radius: R_ic = f R_i, with f=3 following literature^4,43. Assuming that some fraction of the kinetic energy of the impactor is consumed within this volume, the temperature change associated with impact is then given by

$$\Delta T=\frac{1}{C_p}\left[{\left(\frac{R_i}{R_{ic}}\right)}^3\beta {v_{imp}}^2-L_m\right]$$ (4)

where L_m is the latent heat of fusion, v_imp is the impact velocity (given by the N-body simulations) and β is a factor to account for energy delivered beyond the isobaric core. Here we take β=0.5 to provide a conservative estimate of the initial melt temperature. Inspection of this equation shows that a minimum velocity of about 4.6 km/s is required to initiate significant mass loss.

We assume that the pre-impact target material is at the solidus, here taken to be 1400 K. The justification for doing so is that heating by ²⁶Al will melt bodies that formed early enough (to be conservative, we ignore at this stage that such melting induced by ²⁶Al heating could have led to vapour mass loss). Melt advection will rapidly cool the target to 1400 K, but subsequent cooling (by conduction or solid-state convection) will be much slower. We also impose a maximum melt temperature of 3500 K. This is approximately the temperature at which total silicate vaporization is achieved and the physics of mass loss will change. Imposing this cut-off will underestimate the total amount of mass loss.

Although the radius of the isobaric core is somewhat uncertain, varying f does not have a very large effect on our results, because of the trade-offs involved. A smaller isobaric core reduces the surface area and cooling timescale, but it increases the melt temperature (and thus the vapour pressure and the initial mass loss rate). By contrast, the difference between regular and Grand Tack accretion is dramatic. This is because the Grand Tack results in more dynamical excitation, and thus more energetic collisions.

Extended Data Figure 6 plots the median impact velocity normalized to the escape velocity as a function of body radius. The biggest difference between a calm disk (without gas drag) and Grand Tack accretion is that the normalized impact velocities for large bodies are much bigger in the latter. Since no vapour loss happens below a particular cut-off velocity (equation 4), it is clear that Grand Tack simulations will generate much more vapour loss. Increasing β to 1 causes only modest increases in the predicted mass loss for conventional accretion, because impact velocities are still general below the cut-off value.

Implementation: Each body undergoes mass growth by collision; each collision may also lead to some mass loss via vapour outflow. For each impact, we calculate the initial melt pool mass and temperature as outlined in the section Melt pool volume and temperature. The instantaneous mass loss rate is calculated using as described in the section Mass loss rate. Given the mass loss rate, the change in melt pool temperature is calculated according to equation (1). The temperature is updated accordingly and the cycle then repeats. The total mass lost is tracked.

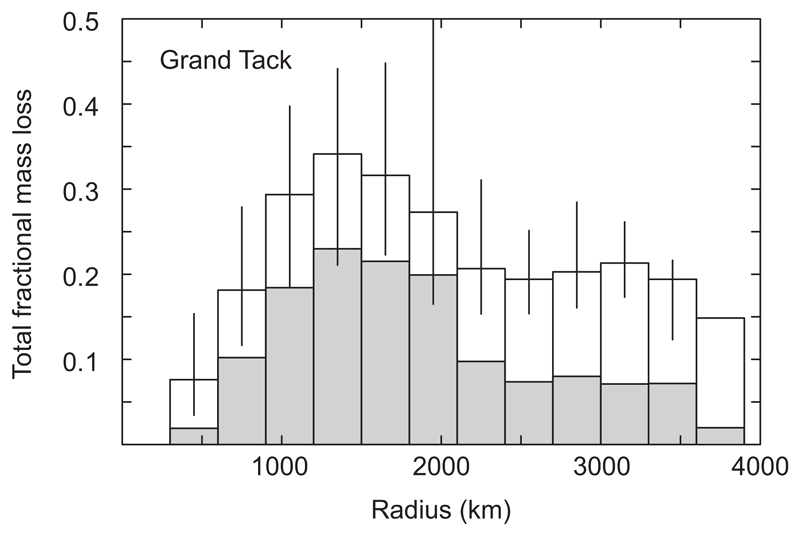
A disadvantage of our approach is that the pre-history of impactors striking a target body is not recorded. Since these impactors have likely undergone mass loss of their own, our approach may therefore underestimate the total fractional mass loss of the final body. To mitigate this problem, for the Grand Tack results we perform a two-step calculation. In the first step we calculate the total mass loss for each body neglecting inheritance effects. We use these results to determine the median mass loss over all bodies within a particular final mass range. The median prior fractional mass loss ϕ determined in this manner for the GT bodies is given by the following empirical formula:

$$\varphi =0.4\times {10}^{-5}{R}_s^{1.65}{e}^{-0.65\times {10}^{-5}{R}_s^{1.65}}$$

where R_s is in km. We then re-run the calculations, this time assuming that each impactor has experienced prior mass loss based on this median value. The results of both calculations are shown in Extended Data Figure 7.

For the conventional accretion simulations without gas present in the disk (“calm disk”) vapour loss is sufficiently small that we neglected this inheritance effect. Extended Data Figure 7 plots the median fractional mass loss for all bodies in the Grand Tack accretion simulations. The simulations for a calm disk result in very limited mass loss, and only for the largest (see Figure 2b in main text). By contrast, mass loss in the Grand Tack scenario is much more extensive.

Vapour-liquid Mg isotope fractionation models

We first consider a kinetic isotope fractionation scenario. For this, we modelled the elemental loss of Mg required to obtain ~0.02‰ heavier Mg isotope compositions by a Rayleigh distillation process with an experimentally determined kinetic isotope fractionation factor⁴⁴ (referred to as ${\alpha }^{25/24}M{g}_{g/liq}^{kin}$) of 0.9860. We obtained a relative mass loss of Mg by vaporization $(f_{Mg}^{vap})$ of 0.14% from $f_{Mg}^{vap}=1-e^{{\delta }^{25/24}Mg/\left({\alpha }^{25/24}M{g}_{g/liq}^{kin}-1\right)}.$ This is a very small mass loss, but we can expect much larger concomitant K mass losses, owing to its higher volatility. Although it is hard to quantify such K loss, we can estimate it from an equilibrium liquid-vapour model (see below), given that kinetic evaporative fluxes (J) from a molten surface are proportional to their saturation vapour pressures as well as the elemental mass⁴⁴. In the simplest scenario, i.e. assuming a single vaporisation event, we find 0.14% of Mg is vaporised at ~2700 K, at which temperature ~28% of K occurs as vapour (all as atomic K). Using a published⁴⁵ ${\alpha }^{40/39}{K}_{g/liq}^{kin}$ of 0.9892 we obtain that ⁴¹K/³⁹K fractionates by ~7‰. This compares to <2.7±1‰ observed fractionation in Solar System material²⁵, underscoring the implausibility of kinetic fractionation.

We also examine an equilibrium liquid-vapour fractionation model. Vapour production results in isotopically light vapour and heavy liquid compositions, thus evolving a vapour depleted bulk planetesimal to isotopically heavier compositions. The composition of silicate vapour in equilibrium with a molten planetesimal was calculated with a thermodynamic model involving equilibrium reactions between silicate liquid and vapour species for nine elements: O, Na, Mg, Al, Si, K, Ca, Ti and Fe. The model is modified from the MAGMA code by Fegley and co-workers^46,47. We followed the approach of these authors to non-ideal mixing in the silicate liquid (i.e. assuming ideal mixing of complex oxide and silicate pseudo-components), used their tabulated thermodynamic data, and, like them, we assumed ideal mixing in the gas. Our approach differs from theirs in that we let go of their constraint that oxygen-to-metal ratios in the gas must be identical to the original liquid. Instead, we used the ideal gas law to convert partial pressures of gas species to number of moles in order to enforce conservation of mass by simultaneously solving mass balance equations for the number of moles of each element. Hence, we have 66 equilibrium equations and nine mass balance equations to solve for activities of 75 species. The disadvantage of our approach is that the ideal gas law adds one freely adjustable parameter in the form of the volume the gas can expand into. We have chosen to fix this volume such that vapour fractions between ~0.001 and ~0.15 were obtained between 2500 K and 3500 K. Such fractions are of similar order of magnitude to the average vapour fraction produced in single collisions in the N-body simulations (note that an order of magnitude variation in the chosen volume leads to ~5 fold variation in the vapour fractions but these changes do not affect our conclusions because their effect is counterbalanced by the number of “collisions” that are run to obtain the observed Mg isotope composition; see below). To convert from activities of the liquid species to moles, which we need for the mass balance equations, we need one more variable, i.e. the total moles of all liquid species, bringing the number of unknowns to 76. However, there is the activity normalisation constraint: the activities (i.e. mole fractions) of liquid species must sum to 1. Hence, we have 76 constraints to solve for 76 variables. The code is easily expandable with extra elements and equilibrium reactions and is freely available from the authors upon request.

In our equilibrium liquid-vapour fractionation model, we used published reduced partition functions (β) to approximate equilibrium Mg, Si and Fe isotope fractionation factors between silicate liquid and atomic silicate vapour. Experimental calibrations of equilibrium isotope fractionation factors between vapour and liquid do not exist to date. As β are currently unavailable for silicate liquid, we approximated them with those for forsterite crystals for Mg⁴⁸ and Si⁴⁹ and fayalite crystals for Fe⁵⁰. We used further literature sources for β for other vapour species MgO_(g)⁴⁸, FeO_(g)⁵¹ and SiO_(g)^49,52. Relative abundances of species in mixed vapours, e.g. Mg(g) and MgO(g), were obtained from the thermodynamic model described above. A two-component mass balance relationship combining isotope compositions of the vapour (subscript g) and the remaining ‘liquid’ (subscript liq) were used to determine the offset relative to the original bulk composition (set to 0 for reference here) prior to loss of a vapour fraction $(f_g):\delta {}^{25/24}M{g}_{liq}=-f_g\delta {}^{25/24}M{g}_g/\left(1-f_g\right).$

We used this equilibrium vapour-liquid fractionation model to simulate vapour loss as various temperature events (i.e. planetary collisions). We initiated the model with a chondritic elemental composition (see main text) and isotope compositions of 0, as mentioned above. We removed 95% of the chondritic Fe assuming it segregated into a core which is not affected by vaporisation. We let a single “collision” affect 20% of the body and assumed that the body undergoes full chemical homogenisation between two events. After the first “collision”, the calculated isotopic and elemental compositions of the residual liquid were then used as initial values for the next “collision”, and so forth. The temperature used to calculate equilibrium vapour-liquid compositions and isotopic fractionation in any “collision” event was obtained by random selection of a temperature uniformly distributed between 2500 K and 3500 K.

Extended Data

Extended Data Figure 1.

Magnesium isotope compositions of carbonaceous chondrites plotted against their average literature oxygen isotope compositions⁵³. These mass-dependent oxygen isotope measurements reflect parent body hydrothermal alteration²⁰, so the correlation (R² = 0.78) between Mg and O isotopes (as well as with petrographic group⁵⁴; indicated in brackets under sample names) implies that the Mg isotope compositions of some carbonaceous chondrites have been altered by hydrothermal processes. The most altered samples, to the upper right of this diagram, are excluded from our chondrite Mg isotope means.

Extended Data Figure 2.

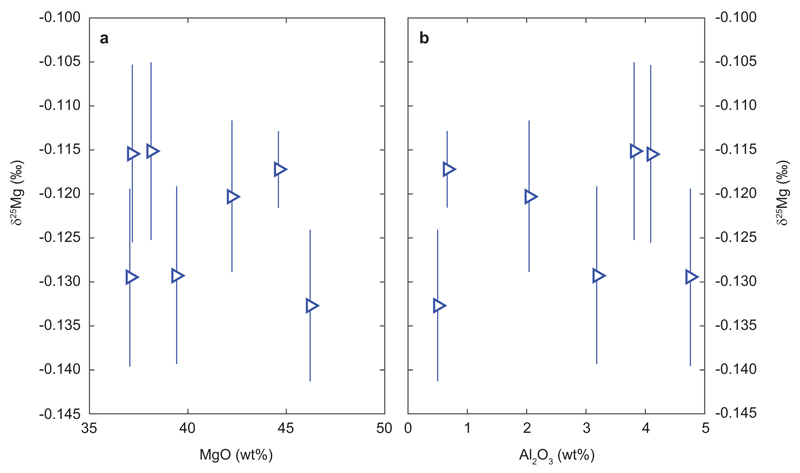
Magnesium isotope compositions of peridotites plotted against whole rock MgO (panel a) and Al₂O₃ (panel b) contents. The absence of correlations of Mg isotope compositions with MgO or Al₂O₃ indicates absence of discernible Mg isotope fractionation during partial melting.

Extended Data Figure 3.

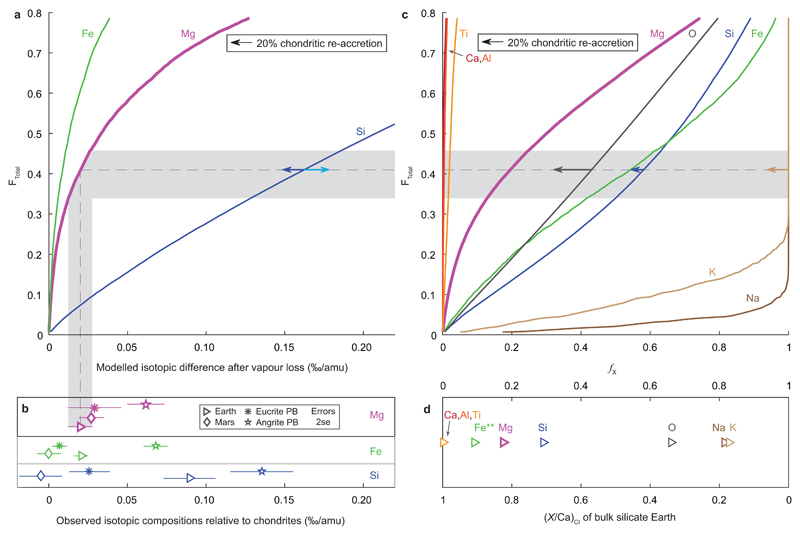
Comparison between modelled compositions of a vapour depleted liquid and observed planetary compositions. As Figure 3 in main text, but additionally including observed isotope compositions for Mars, and eucrite and angrite parents bodies as well as including elemental and isotopic Fe observations (panels b and d; Fe isotope data from [55] and references therein, all other references as in Figure 3). Comparison of observed Fe contents and isotope ratios are complicated by core formation because most Fe enters the core. In our model we assume that the iron in the core has not been affected by vaporisation, inferred to occur later. For instance, the effect of ~48% Fe loss (panel c) on the current bulk silicate Earth Fe content is dependent on the fraction of Fe that entered the core prior to collisional vaporisation and the oxygen fugacity evolution of the growing Earth. For reference, the datum labelled Fe** in panel d is therefore the Fe/Ca of the bulk Earth (calculated from [56]) instead of the Fe/Ca of the bulk silicate Earth. Similarly, Si can also enter the core, although its quantity is likely <3 wt%⁵⁷. Right pointing arrows in b) and d) indicate the effect of 3 wt% Si in the core (3000 K assumed for metal-silicate Si isotope fractionation factor⁵⁸).

Extended Data Figure 4.

Comparison between modelled compositions of a vapour depleted liquid and observed planetary compositions. Similar to Extended Data Figure 3, but for model runs with a CI chondrite initial composition. Observed Mg and Fe isotope compositions (panel b) are presented relative chondrite mean, while Si isotope observations are relative to a mean of carbonaceous and ordinary chondrites⁵⁹, because those chondrites have undistinguishable Si isotope compositions, yet are distinctly different from enstatite chondrites (see [4] and references therein).

Extended Data Figure 5.

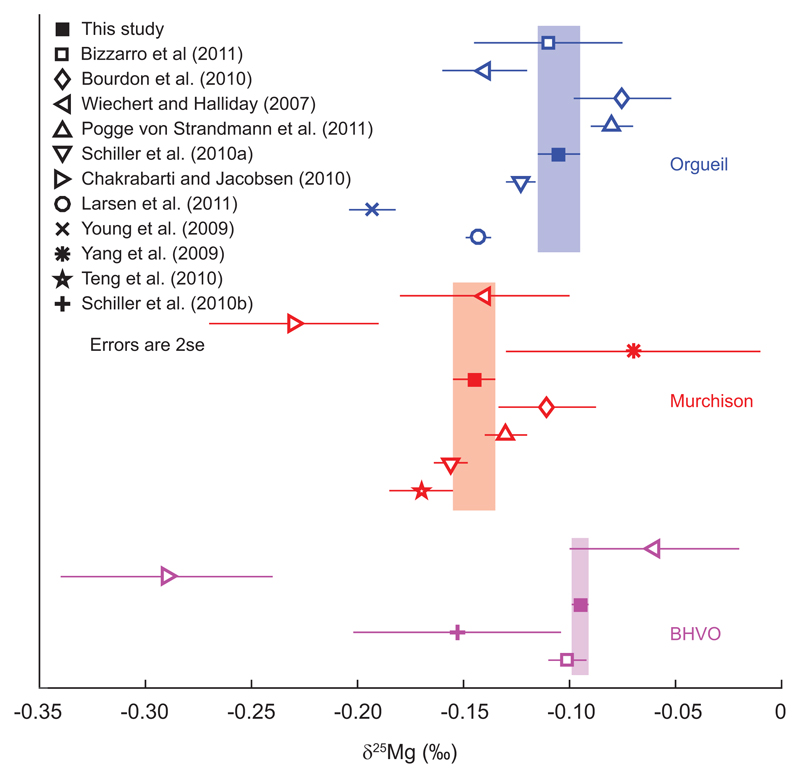
Magnesium isotope compositions of reference samples analysed in multiple studies. The shaded areas show the mean and 2se of the isotope compositions observed in this study. Note that the plotted composition of Murchison for Bourdon et al.¹⁰ is a mean of the two replicates presented in their Table 1. The value for BHVO of Chakrabarti and Jacobsen¹⁶ is BHVO-1, all others are BHVO-2.

Extended Data Figure 6.

Variation in velocity of individual impacts (normalized by target body escape velocity) as a function of target body radius. Central line denotes median value, shaded box encompasses region spanning 25^th-75^th percentiles, upper lines denote 90th percentile. Bulk density assumed to be 3000 kg m^-3.

Extended Data Figure 7.

Fractional mass loss in Grand Tack simulation as a function of final body radius for direct vapour outflow model to illustrate results both with (white boxes, as Figure 2b) and without (shaded boxes) the inclusion of inheritance effects (see Methods). Boxes denote the median value, bars denote the 25^th and 75^th quartiles.

Extended Data Table 1.

Sample sources and weights of digested sample from which aliquots were taken for Mg isotope analysis in this study. NHM is Natural History Museum, London, UK. NASA is National Aeronautics and Space Administration. ¹Aliquot from a homogenised powder of several grams.

Meteorites	Source	Sample weight digested (mg)	Identification number
Orgueil	NMH	98.14	BM 36104
Ivuna	NHM	11.6	BM 1991, M5
Al Rais	NHM	4.6	BM 1971, 289
Renazzo	NHM	4.4	BM 41105
Kainsaz	NMH	69.34	BM 1988,M24
Murchison	NMH	86.92	BM 1970,6
Parnallee	NMH	6.37	BM 34792
Dhurmsala	NHM	12.69	BM 96262
Ceniceros	NMH	46.93	BM 1989,M31
Zag	Meteorite dealer	7.181	-
Khairpur	NMH	69.39	BM 51366
Hvittis	NHM	45.8	BM 86754
Yilmia	NHM	29.8	BM 1972, 132
St Mark’s	NMH	60.37	BM 1990, 339
Abee	NHM	66.7	BM 1997, M7
Indarch	NHM	97.0	BM 1921, 23
ALHA 77005	NASA	71.99	ALHA77 005, 234
DaG 476	Meteorite dealer	91.78	-
EETA 79001	NASA	121.19	EETA79 001, 665
RBT 04262	NASA	89.09	RBT 04 262, 61
Zagami	Meteorite dealer	61.00	-
LAR 06319	NASA	95.58	LAR 06 319, 59
Johnstown	NHM	133.31	BM 1959,828
Shalka	NHM	155.58	BM 33761
Tatahouine	NHM	112.89	BM1931,490
d’Orbigny	Meteorite dealer	15.281	-
Terrestrial			Location
BZ116	ref 51	7.891	Bozu section, Horoman peridotite, Japan
Vi 313-102	ref 52	23.971	Vitim volcanic field, Russia
BZ143	ref 51	4.231	Bozu section, Horoman peridotite, Japan
BZ-29	ref 53	12.971	Zabargad Island, Egypt
Vi 314-56	ref 52	10.391	Vitim volcanic field, Russia
BZ251	ref 51	11.931	Bozu section, Horoman peridotite, Japan
2370-1	ref 54	3.39	9-10°N East Pacific Rise
DS12-29	ref 55	3.92	26°S Mid-Atlantic Ridge
9/30a(1)	ref 56	2.07	57°E South-West Indian Ridge