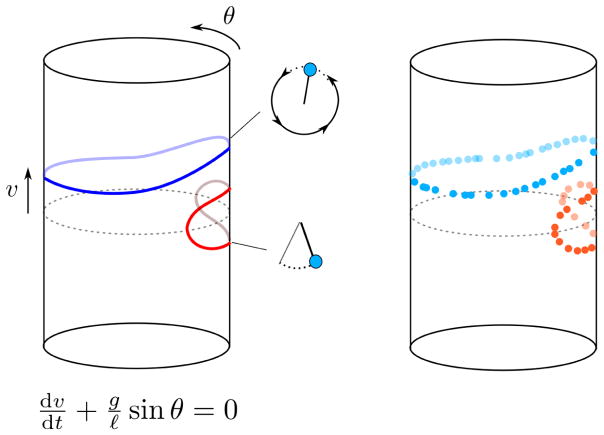
Figure 1. The phase space of a simple pendulum without friction.

The phase space of a simple pendulum is a two-dimensional cylinder, where the periodic coordinate corresponds to the angle (θ) of the pendulum with respect to the vertical, and the longitudinal coordinate to its angular velocity (v). Each point in this space specifies a unique combination of the position and velocity and uniquely determines the subsequent evolution. For small angular velocities, the pendulum oscillates back and forth around the equilibrium point. For large velocities, the pendulum describes a circular motion. These two regimes are represented by qualitatively different trajectories in the phase space which cannot be continuously deformed into each other (in mathematical terms, they are homotopically inequivalent). By just looking at the shape of the trajectories in the phase space, we can extract information about a dynamical system. The dynamics of the simple pendulum is fully described by a differential equation depending on the length of the pendulum (ℓ) and the acceleration of gravity (g). In biological systems the mathematical equations describing trajectories in the phase space are usually unknown, but current technologies allow to reconstruct trajectories from high-throughput measurements.