Cellular Contraction Can Drive Rapid Epithelial Flows

Abstract

Single, isolated epithelial cells move randomly; however, during wound healing, organism development, cancer metastasis, and many other multicellular phenomena, motile cells group into a collective and migrate persistently in a directed manner. Recent work has examined the physics and biochemistry that coordinates the motions of these groups of cells. Of late, two mechanisms have been touted as being crucial to the physics of these systems: leader cells and jamming. However, the actual importance of these to collective migration remains circumstantial. Fundamentally, collective behavior must arise from the actions of individual cells. Here, we show how biophysical activity of an isolated cell impacts collective dynamics in epithelial layers. Although many reports suggest that wound closure rates depend on isolated cell speed and/or leader cells, we find that these correlations are not universally true, nor do collective dynamics follow the trends suggested by models for jamming. Instead, our experimental data, when coupled with a mathematical model for collective migration, shows that intracellular contractile stress, isolated cell speed, and adhesion all play a substantial role in influencing epithelial dynamics, and that alterations in contraction and/or substrate adhesion can cause confluent epithelial monolayers to exhibit an increase in motility, a feature reminiscent of cancer metastasis. These results directly question the validity of wound-healing assays as a general means for measuring cell migration, and provide further insight into the salient physics of collective migration.

Introduction

When cells migrate to close a wound or remodel tissue, they often move as collective groups or sheets (1). This collective cell migration is, at least partially, due to cell-cell adhesion and shows strikingly different behavior than the migration of individual cells (2). The standard in vitro technique for studying collective migration is the wound-healing assay, which involves observing groups of cells moving across a free surface created by either the removal of a barrier or by physically scratching away cells (2, 3). For example, these assays have been used to study the migratory potential of tumor cells (4, 5, 6, 7) or the re-epithelialization process (2, 8). Many previous studies have shown that after confluent epithelial cells are presented with a free surface, migration begins with the leading-edge destabilizing to form migration fingers that are guided by phenotypically different cells at their tips, known as leader cells (2, 9, 10, 11, 12). These leading cells exert large traction forces that allow them to pull on the cells behind them, thus driving the advance of the wound border (13). However, developmental processes in vivo, such as branching morphogenesis, lack defined leaders and are driven forward by multiple cells that dynamically rearrange their positions (10, 14).

Coordinated motion requires coordinated force. Although many experimental investigations have examined traction force distributions during wound healing (13, 15, 16, 17, 18), how single cells coordinate to drive collective migration remains unknown. Recently, there have been several physical theories proposed to describe collective migration, primarily aimed at explaining the complex motions that occur during wound-healing assays. Although these models use different theoretical frameworks, including discrete propelled point particles (19, 20), hybrid cellular models such as Dirichlet domains (21, 22) or the Cellular Potts Model (23, 24), and continuum-level approaches (25, 26, 27), they all consider the importance of single-cell forces and are primarily based on the notion that collective behavior arises from the constrained motion of adhered single cells. Because the models are posed in different mathematical representations, it is difficult, even for experts, to judge the similarities and differences between these models (28, 29), and there has yet to be a clear effort to identify whether any or all of these models can accurately predict how cellular or global perturbations alter collective behavior.

In this study, we directly investigated the correlation between the physical characteristics of individual cells and collective cell migration. For our experiments, we chose Madin-Darby canine kidney (MDCK) epithelial cells because they are the prototypical cell-line used in wound-healing experiments (2, 13, 15, 17, 30, 31, 32). Here, we study the behavior of MDCK type I and type II cells. We chose to look at these two cell types because they are both derived from the parental MDCK (NBL-2) strain; however, MDCK I cells spread more on surfaces and are more migratory (along with having other differences in cell junctions, morphology, and apical membrane proteins; see (33)). In addition, both of these cell types have been used extensively in the literature to study epithelial polarity and dynamics (33). To perturb cellular dynamics, we chose to alter the adhesive interaction between the cells and the substrate using fibronectin (FN) and poly-L-lysine (PL) coated substrates, because FN promotes integrin binding (34) and PL binds nonspecifically to anionic substances on the cell surface (35). We measured the motility and morphology of individual MDCK I cells on fibronectin (I-FN) or poly-L-lysine (I-PL), and individual MDCK II cells on fibronectin (II-FN) or poly-L-lysine (II-PL), and then quantified the collective migration of these cells on these same substrates using wound-healing assays. For clarity, we have assigned each cell-type/substrate combination a specific color that is used throughout the work presented here: I-FN (red), I-PL (green), II-FN (magenta), and II-PL (blue). Surprisingly, we find that cell speed at the single-cell level is not indicative of wound closure rates; i.e., cells that move slowly as individuals can migrate rapidly in collectives and vice versa. Guided by predictions from an existing mathematical model (25, 27), we show that this speed enhancement is attributable to an increase in single-cell intracellular contractile stress. In addition, for all cell/substrate combinations except II-PL, migration rates of wound borders do not depend on leader cells, and confluent epithelial dynamics cannot be predicted by appealing to results from the literature on jamming in active matter (22). Finally, we show that changes in single-cell intracellular contractile stress and adhesion can increase motility in confluent epithelial monolayers, transitioning a stationary epithelium into a dynamic, migratory population, consistent with a mathematical model that considers single-cell physics, contraction, and adhesion. Taken together, our study links single-cell force production to multicellular motion, shedding light on the fundamental mechanisms of collective cell migration (26, 27).

Materials and Methods

Cell culture

MDCK type I and type II epithelial cells were a generous gift from J. Wilson (University of Arizona, Tucson, AZ). The cells were cultured in Dulbecco’s modified Eagle’s media (Cellgro) supplemented with 10% fetal bovine serum (Omega) and 1% antibiotics solution (penicillin (10,000 units/mL) + streptomycin (10,000 μg/mL); Gibco) at 37°C and 5% CO₂.

Single-cell measurements

Low-density (2500 cells/cm²) MDCK I and MDCK II cells were grown in sterile, two-chamber dishes (Lab-Tek II). The dish surfaces were coated with either 2 μg/mL FN solution (Sigma-Aldrich) for at least 1 h at 37°C (2), or 5 × 10^−6% PL (Sigma-Aldrich), diluted in PBS and allowed to dry at room temperature. The dishes were then rinsed with sterile 1× PBS and the cells were cultured for 12–24 h in the incubator at 37°C, with 5% CO₂ and 90% relative humidity. The cells were imaged using a Zeiss Axio Observer inverted, wide-field microscope using a 20× air, 0.8 numerical aperture (NA) objective equipped with a Hamamatsu ORCA Flash 4.0 CMOS camera. The microscope was equipped with a CO₂ Module S (Zeiss) and TempModule S (Zeiss) stage-top incubator (Pecon) that was set to 37°C, with 5% CO₂ for long-time imaging. Images were captured every 3 min for 12 h using differential interference contrast (DIC) microscopy. Individual cells were tracked using a custom-written MATLAB algorithm to segment the images. The center of mass of each cell was then determined in each frame and the velocity was computed as the change in center of mass position between frames. Only cells that were accurately tracked for at least 50 frames were analyzed. The persistence time, P, was computed by fitting the mean-squared displacement, MSD, for each cell to the following formula (36): MSD(τ) = c (exp(−τ/P) + τ/P – 1), where c is a constant.

Wound-healing measurements

The epithelial cells were grown to confluency (160,000 cells/cm² for MDCK I cells and 200,000 cells/cm² for MDCK II cells) on either PL or FN coated slides, as described above. Scratch assays were performed by scraping a sterile scalpel across the bottom of the dish to create a “wound.” Cell debris was washed away by rinsing with sterile 1× PBS. The PBS was then removed from the dish and 2 mL growth media was added. Images were captured every 5 min for 14 h using the microscope system described above and a 20× air (0.8 NA). Wound edge detection and measurement of intralayer velocity fields were performed by automatically determining the wound edge by segmenting the images based on intensity. The average border velocity is given by the change in area of the wounded region divided by the perimeter of the wound edge. The intralayer velocity is the average magnitude of the velocity field of cells that are at least 150 pixels (45 μm) back from the wound edge, where the flow field is determined using an optical flow algorithm (37, 38). Wound edge velocity and intralayer velocities were measured for all frames of the images (168 frames per movie) and were found to be fairly uniform in time. Edge velocities were sometimes excluded from our analysis due to imprecise segmentation. Likewise, intralayer velocities were omitted from analysis in cases where the velocity field tracked motion of debris in the background.

Confluent epithelial monolayer measurements

Epithelial monolayers were grown to confluency (160,000 cells/cm² for MDCK I cells and 200,000 cells/cm² for MDCK II cells) on FN or PL coated dishes. Images were captured every 5 min for 14 h using a 20× (0.8 NA) objective. Intralayer flow fields were extracted using an optical flow algorithm (37, 38).

The displacements within the monolayer were determined using simulated tracer particles. We seeded the first frame of a time-lapse movie with 100 randomly distributed tracer particles. The trajectories of these particles were then simulated using a forward Euler method to integrate the positions of the particles given the extracted, time-dependent intralayer velocity fields. Overlaying the particles on the DIC images showed that the particles followed the motions of the cells (Movie S7).

Traction force microscopy

Silicone substrates for traction force microscopy (TFM) were prepared following the procedure in Mertz et al. (39). Briefly, silane (3-aminopropyl triethoxysilane) (Sigma-Aldrich) was vapor-deposited onto a 29-mm glass-bottom dish with a 14-mm microwell (In Vitro Scientific). Fluorescent beads were covalently attached to the surface by filling the dish with a fluorescent bead solution containing dark-red fluorescent (580/605) carboxylate-modified microspheres with a radius of 100 nm (Life Technologies), at a volume ratio of 1:3000 and 0.1 mg/mL of 1-ethyl-3-(3-dimethylaminopropyl) carbodiimide in borate buffer solution (pH ∼7.4). Silicone elastomer was then prepared by mixing a 1:1 weight ratio of CY52-276A and CY52-276B (Dow Corning Toray). The elastomer was vacuum degassed for ∼5 min to eliminate bubbles, the polymer was then spin-coated onto the microwell of the dish at 1000 Rpm for 60 s. The dish was cured overnight and resulted in a ∼30-μm-thick layer of silicone. Silane was then vapor-deposited again on top of the now cross-linked elastomer and a second layer of fluorescent beads was deposited at a volume ratio of 1:1000 and 0.1 mg/mL of 1-ethyl-3-(3-dimethylaminopropyl) carbodiimide in borate buffer. The dish was allowed to dry before being coated with FN (20 μg/mL; Sigma-Aldrich), which sat at room temperature for ∼20 min before being washed with PBS. We estimated the Young’s modulus, E, of the cured elastomer to be ∼3 kPa (39, 40).

Cells on top of the TFM substrates were maintained at 37°C and 5% CO₂ using a stage-top incubator and heated stage. Images for TFM experiments were captured with the microscope system described above, using a 40× (1.2 NA) water-immersion objective. As cells adhered to the surface, we acquired epifluorescence images of the stressed state of the top layer of fluorescent beads and the bottom bead layer, as well as a DIC image of the cells. Trypsin-EDTA (0.25%; Life Technologies) was then used to remove the cells from the surface, and a set of epifluorescence images of the top and bottom layers of beads was acquired. The trypsin treatment did not produce noticeable deformations of the substrate (Fig. S4).

The displacements between the stressed (with cells) and unstressed (without cells) state of the beads were calculated using the MATLAB algorithm described in Style et al. (40). The DIC images were segmented to identify cells. Because traction force measurements are known to smear the forces over distances that are larger than the cell (41), we dilated the segmented images, typically using a morphological dilation operation with a disk kernel of radius 15 pixels. At times, a slightly smaller or larger dilation kernel was used to prevent over- or under-representation of the traction force smearing. The average magnitude of the traction force was then computed over this region.

Results

Substrate effects on isolated MDCK cell motility

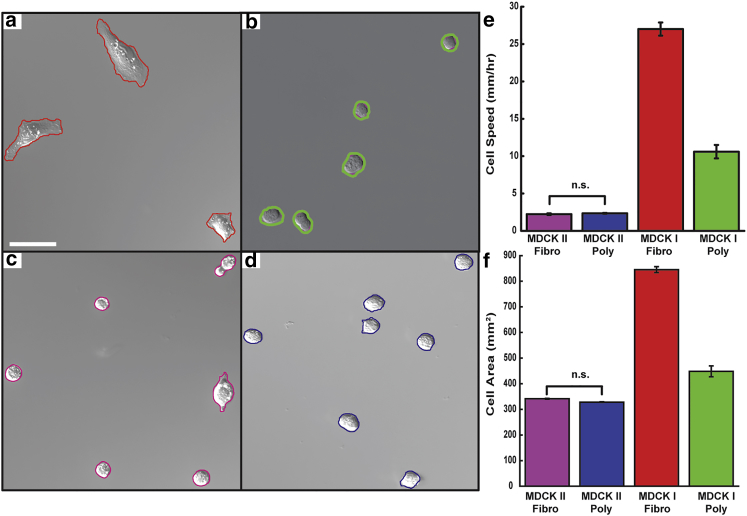
To determine how single-cell biophysics influences collective migration, we began by quantifying the motility of individual cells. Cells at low density were allowed to adhere to FN or PL coated surfaces and were then imaged at 3 min intervals for 12 h. Cell motility and morphology were characterized by segmenting DIC images and measuring cell centroids, areas, and perimeters (Fig. 1, a–d; Movies S1 and S2). Instantaneous velocities were computed from the change in centroid position between frames. We found that the I-FN cells were highly dynamic, with an average cell speed of 27 ± 1.0 μm/h, whereas on PL their speed decreased by ∼3-fold to 10 ± 0.4 μm/h. MDCK I cells were always more mobile than MDCK II cells, whose average speed of 2.3 ± 0.1 μm/h was not strongly affected by surface alterations (Fig. 1 e; Fig. S1).

Figure 1.

The motility and morphology of MDCK epithelial cells on coated surfaces. Cell contours of MDCK type I cells on (a) FN (red) and (b) PL (green) and MDCK type II cells on (c) FN (magenta) and (d) PL (blue) were automatically tracked from DIC images taken at 3 min intervals over 12 h time periods. Average cell speeds (e) and areas (f) were measured for each combination (p < 0.05, Tukey test unless otherwise specified; I-FN, n = 255; I-PL, n = 413; II-FN, n = 246; II-PL, n = 665). Error bars are mean ± SE; scale bar, 50 μm. To see this figure in color, go online.

The morphology of MDCK I and MDCK II cells were noticeably different. We found that MDCK II cells were less spread and more circular than MDCK I cells (Fig. 1 f; Fig. S1). In addition, substrate adhesion did not greatly alter cell shape or area for MDCK II cells (area ∼330 μm² on both surfaces) (Fig. 1 f; Fig. S1), but we found a marked difference in area for MDCK I cells, with an average cell area of 845 ± 12 μm² on I-FN and 448 ± 21 μm² on PL (Fig. 1 f).

Isolated cell speed is not indicative of wound-healing dynamics

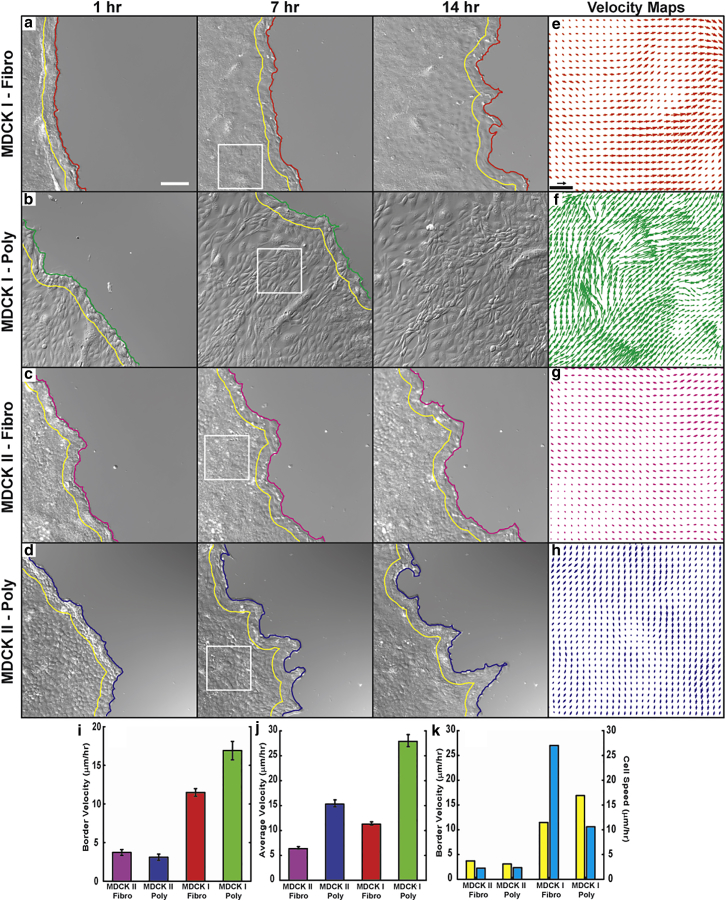
We performed scratch assays to investigate wound-healing dynamics using the same cell types and surface coatings. Wound border velocities were measured from segmented images of the wound region and intralayer cell velocity fields were determined using a gradient-based optical flow method (37, 38) (Fig. 2, a–h; Fig. S2, a and b; Movies S3 and S4). We expected to find that border and intralayer velocity measurements were correlated with one another and also with individual cell speed. For example, we expected that the I-FN cells would show the largest velocities in these assays. Surprisingly, this was not the case. Although the average border velocity for the I-FN cells was 11 ± 0.5 μm/h, the I-PL wounds exhibited an average border velocity of 21 ± 2 μm/h (Fig. 2 i). We found that the intralayer velocity fields had average speeds that were roughly comparable to the rate of the wound-border advance, with I-PL cells moving significantly faster than I-FN cells (Fig. 2 j). In other words, although wound closure and monolayer speeds on FN was inhibited nearly threefold compared with single-cell motility, these collective dynamics were enhanced on PL by a factor of two. This more dynamic velocity field also produced shorter velocity correlation lengths for the I-PL cells compared with the I-FN cells (Fig. S2 c).

Figure 2.

Wound-healing dynamics are affected by surface coating. The leading edge of wounded (a) I-FN (red), (b) I-PL (green), (c) II-FN (magenta), and (d) II-PL (blue) were tracked over 14 h periods. A region ∼150 μm behind the border (yellow lines) was used for intralayer velocity measurements. II-PL cells showed two distinct behaviors: slow, steady advance of the border (d), and retraction (Fig. S1a). Scale bar, 300 μm. Representative velocity fields from (a)–(d) are shown for (e) I-FN (red), (f) I-PL (green), (g) II-FN (magenta), and (h) II-PL (blue), with the white boxes in (a)–(d) indicating the corresponding time and location of these subregions. Scale bar, 50 μm; arrow represents a velocity of 30 μm/h. (i) Average border velocities for each scenario (p < 0.05, two-sample t-test for all cases unless otherwise specified; I-FN, n = 135; I-PL, n = 33; II-FN, n = 71; II-PL, n = 6). (j) Average intralayer velocities were measured for all cases (p < 0.05, Tukey test, unless otherwise specified; I-FN, n = 130; I-PL, n = 42; II-FN, n = 69; II-PL, n = 28). Error bars are mean ± SE. (k) Average border velocity (blue) does not correlate with isolated cell speed (yellow). To see this figure in color, go online.

Because the migration of the MDCK II cells were not strongly affected by substrate coating, we did not expect to find substantial differences between the wound-healing dynamics for MDCK II cells on these substrates. As expected, the II-FN cells had slower wound border speeds and intralayer velocities than either the I-FN or I-PL cells, with an average wound speed of 3.7 ± 0.4 μm/h and an average intralayer speed of 6.4 ± 0.2 μm/h (Fig. 2, i and j). However, on PL the wounded MDCK II cells exhibited two distinct types of motions. The first type was similar to that seen with the II-FN cells: a slow, relatively constant migration into the denuded region (Fig. 2, c and d). In the other phase, the border pulled inward, resulting in a negative average border velocity (Fig. S2, a and d). Despite the variation in the direction of the border advancement for II-PL, no difference in the velocity fields within the monolayer was measured (Fig. S2 e).

Although it would seem reasonable that cells that move faster when isolated would also move faster as a collective than cells that move slower when isolated, comparison across our four experimental conditions showed that there is no correlation between isolated cell speed and collective dynamics (Fig. 2 k).

Wound closure does not depend on leader cells or jamming

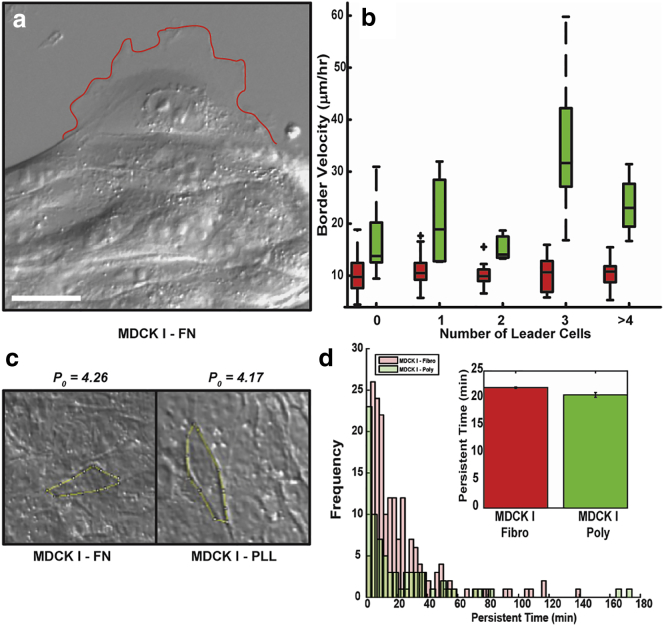
Many groups have described the importance of finger-like projections driven by leader cells to wound-healing dynamics (2, 9, 12, 13, 42), although others have mentioned glass-like dynamics and jamming of active matter (22, 43, 44, 45, 46). Our data allowed us to examine the effects of both of these mechanisms. Under most of our conditions, we rarely observed migration fingers, even when cells that resembled leaders were present near the border (Fig. 3 a). To determine whether the migration dynamics that we previously observed were dependent on the number of leader cells, we measured the average border velocity as a function of the number of leader cells in a field of view (Fig. 3 b; Fig. S2 k). We found that in all but one case (i.e., for the I-FN, I-PL, and II-FN cells), the frequency of leader cells did not influence wound closure rates (Fig. 3 b; Fig. S2 f); however, for the II-PL cells there was a correlation between the number of leader cells and wound border advance (Fig. S2 f). For this singular case, the presence of leader cells helped stabilize the border and drove finger-like projections that helped pull the collective into the denuded region, similar to what other groups have described (Movie S4) (2, 32). Because finger-like projections cause the border to be rougher (i.e., less straight), we also compared border shape to the wound velocity and found that there was not a statistically significant correlation (Fig. S3).

Figure 3.

Leader cells and single-cell speed are insufficient to explain wound dynamics. (a) Characteristic leader cell observed in our experiments, identified by the perimeter of the lamellipodium (red line) being two- to threefold larger than a typical cell on the boundary (12, 58). Scale bar, 20 μm. (b) The border velocity does not depend significantly on leader cell number for I-FN (red), I-PL (green), or II-FN, but does increase for MDCK II cells on PL (Fig. S1f). Box-and-whisker plots indicate the median, extrema, quartiles, and outliers for the indicated number of leader cells (n). (c) Cell perimeters are measured manually in ImageJ (59) (yellow contours) and used to compute the ratio of perimeter to the square root of cell area, p₀. The values of this parameter for the cells shown are 4.26 (I-FN) and 4.17 (I-PL). (d) Histogram of the persistence times computed by fitting mean-squared displacements from isolated cell movements for I-FN (red) and I-PL (green) to a persistent random walk model. Inset shows the corresponding average values for the persistence times. To see this figure in color, go online.

In dense colloidal or molecular systems, crowding of the constituent parts can lead to coordinated motions on length scales larger than the individual components (43). In these systems, density, temperature, and stress are the control parameters that dictate when jamming occurs (47). It has been suggested that confluent epithelial layers may behave in an analogous way to systems near the jamming transition (43). Recent work has suggested that the equivalent control parameters for cellular systems are the ratio of cell perimeter to the square root of the area (p₀), persistence of motion (average length of time that a cell moves in a given direction), and cell speed (22). Here, the ratio p₀ is measured in the confluent layer, where the cell speed and persistence of motion reflect parameters from isolated cells. This model predicts that a two-dimensional, jammed cellular system will have p₀ = 3.81, and that increases in any of these parameters should drive the system away from the jamming transition (22). Therefore, because our I-PL cells are more dynamic in wound-healing assays than the I-FN cells, they should be further from being a jammed system. However, the fact that they move slower when isolated is not consistent with being further away from the jamming transition. It could be that the other two control parameters account for the discrepancy. Therefore, we measured these two control parameters (Fig. 3, c and d). We found p₀ values of 4.15 ± 0.06 (I-FN) and 4.02 ± 0.04 (I-PL) and persistence times of 22 ± 2 min (I-FN) and 20 ± 4 min (I-PL) (Fig. 3, c and d). These findings show that neither of these systems is jammed, because p₀ > 3.81 for both cases. However, it also shows that even if this value of p₀ accurately reflects when a system is jammed, the jamming concept does not provide a useful framework to understand how these collective systems behave away from the jamming transition. For example, because there are only minor differences in p₀ and the persistence time between I-PL and I-FN cells but there are substantial differences in isolated cell speed, it suggests that the I-FN cells should be further from the jamming transition than the I-PL cells, and consequently, should move faster as a collective. Therefore, our data shows that the physics of jamming, at least as described by the model in (22), does not provide a useful conceptual framework for understanding systems that are not jammed, such as the collective motions of MDCK cells.

Intracellular contractile stress is indicative of wound-healing dynamics

Many of the computational models put forth for collective migration drive the active component of cell movements solely with a propulsive force, with some using leader cells to accentuate the dynamics (19, 20). These models would suggest that cell speed and/or leader cells should correlate with border velocity. If these factors do not drive wound-healing dynamics, then what does? One alternative is intracellular contractile stress, the importance of which was proposed in a continuum-level model for wound healing by Lee and Wolgemuth (25, 26, 27). This model considers four separate forces involved in collective migration, a propulsive force proportional to the isolated cell speed, intracellular contractile stress, and resistive forces due to adhesion between the cell and substrate and the cell and its neighboring cells. The contractile stress can be approximately measured using TFM (Fig. 4 a), with the average traction force f_o times the cell diameter (or square root of the cell area) being roughly equal to the contractile stress in the mathematical model (note that because this model is two-dimensional, stress has units of force/distance). To determine whether intracellular contraction stress correlated with the velocities in our epithelial monolayers, we used TFM to measure the average traction force, f_o (Fig. 4, a–c). Then, using cell areas determined from our wound-healing videos (163 ± 6 μm² for I-FN and 150 ± 6 μm² for I-PL), we computed the average intracellular contractile stress and found that it was ∼1.5 times lower for I-FN (0.2 nN/μm) than for I-PL cells (0.3 nN/μm) (Fig. 4 c). Interestingly, II-FN cells had a substantially larger contractile stress than II-PL (Fig. 4 c).

Figure 4.

Contractile stress correlates with wound closure rate. (a) Schematic representation of traction force microscopy. A cell (green lamellipodium and purple nucleus) is imaged on top of a flexible poly(dimethylsiloxane) substrate (tan) of height h ∼30 μm that has fluorescent beads (red) embedded in the top and bottom layers. Intracellular contraction transmits forces to the substrate that displace the top layer of fluorescent beads. (b) These displacements are used to compute the traction forces exerted by the cell on the substrate (40). Scale bar, 10 μm; arrow represents a traction force of 30 Pa. (c) The average magnitude of the traction stress was determined for all cell/substrate combinations. (p < 0.05, Tukey test unless otherwise specified; I-FN, n = 40; I-PL, n = 30; II-FN, n = 45; II-PL, n = 26). Error bars are mean ± SE. To see this figure in color, go online.

Contractile stress can explain epithelial dynamics

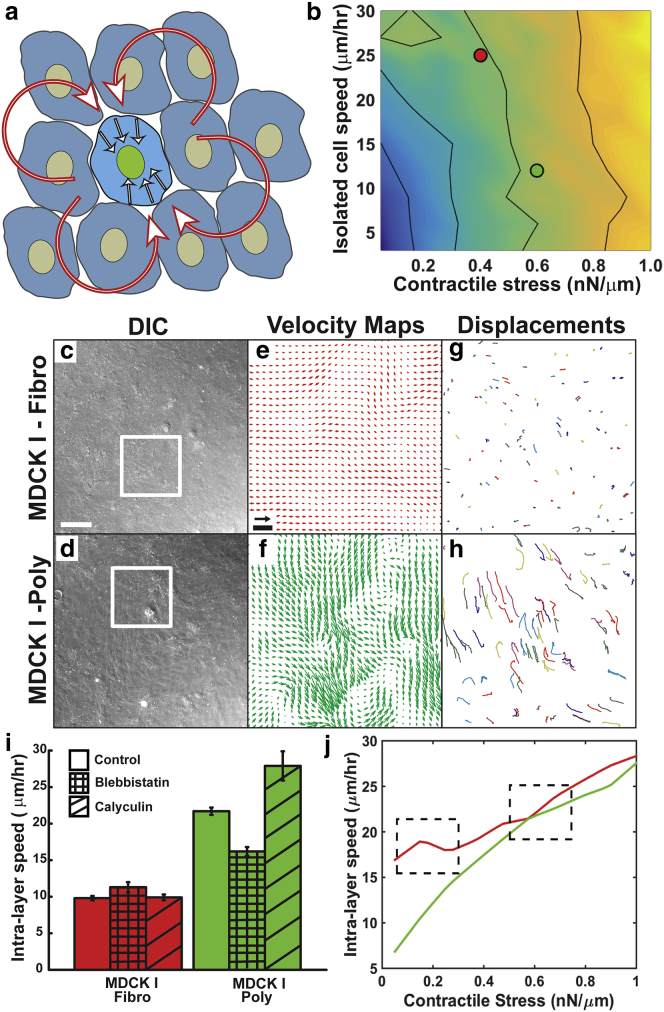
The Lee and Wolgemuth model suggests that contractile stresses generated by the cells can drive fluid-like flows in an epithelial monolayer. Contraction along a preferred axis tends to cause neighboring cells to move in a circulating pattern; i.e., there is a tendency for rotational flow about a contracting cell (Fig. 5 a). These flows torque the cells, driving the orientations of neighboring cells out of alignment and leading to large-scale motions, much like the complex fluid flows in dense suspensions of swimming bacteria (48, 49). To determine whether this model could account for how the slower isolated I-PL cells increased speed when in the collective, whereas the I-FN cells were slower in the collective than as individuals, we simulated a confluent layer of cells using the model described in (27). Simulations were run on a 400 × 400 μm periodic domain using an 80 × 80 grid, a time step of 0.002 h, and the parameters given in Table S1. We varied the isolated cell speed and contractile stress in the model over ranges of 3–30 μm/h and 0.05–1.0 nN/μm, respectively. Simulations are started with random orientations. Within 5 h, the initial random motion evolves into a spatiotemporally varying pattern of vortices and streams (Movie S5). Using these simulations, we computed the average speed in the monolayer over the last 7.5 h of each simulation for each pair of isolated cell speed and contractile stress values (Fig. 5 b). For the parameters that we used, we found that the model predicts that the contractile stress is the more dominant factor in controlling collective migration speed than the isolated cell velocity. Indeed, for isolated cell speed of 25 μm/h and contractile stress of 0.4 nN/μm (similar to I-FNs), we found an average confluent layer velocity of 19 μm/h, whereas for isolated speed of 12 μm/h and contractile stress of 0.6 nN/μm (similar to I-PLs), the model predicts an average intralayer speed of 22 μm/h (Fig. 5 b). Although these values do not exactly match our experiments, the model predicts the correct behavior semiquantitatively, with the I-FN parameters leading to intralayer speeds that are slower than the isolated cell speed, and I-PL parameters leading to intralayer speeds that are nearly twofold faster than the isolated cell speed.

Figure 5.

Cellular contraction and adhesion can produce highly dynamic confluent epithelia. (a) Schematic showing how intracellular contractile forces (white arrows) in one cell can drive flow of nearby cells. The flow field induced by the contraction of the cell center is shown as the red arrows. (b) Predictions from the continuum model for collective migration (25, 26, 27) on how isolated cell speed and contractile stress affect the average velocity of cells in a monolayer (colormap). The colormap ranges from 3 μm/h (blue) to 30 μm/h (yellow) and the black contours show 10, 15, 20, and 25 μm/h. The corresponding values of the isolated cell speed and contractile stress for I-FN (red dot) and I-PL (green dot) are shown. Confluent monolayers of I-FN (c) and I-PL (d) were imaged for 5 h. Scale bar, 70 μm. (e–g) Characteristic velocity fields from the subregions (white boxes) shown in (c)–(d). Velocity fields are color coded as described in the text. Scale bar, 50 μm; arrow represents a velocity of 35 μm/h. (g–h) Trajectories of simulated tracer particles were used to measure the displacements of cells in the monolayer. (i) Drug treatments on confluent layers of I-FN and I-PL cells. Blebbistatin treatment accentuates the speed of I-FN slightly slows I-PL down (crosshatched bars) compared with controls (open bars), whereas calyculin A speeds up I-PL but has little effect on I-FN (diagonal lines). (j) These results are consistent with the model that shows a monotonically increasing dependence of intralayer speed on contractile stress for parameters that correspond to I-PL cells (green line), but nonmonotonic behavior for parameters that correspond to I-FN cells (red line). Boxed regions surround the appropriate parameter regimes. To see this figure in color, go online.

These simulations were run on a continuous, periodic domain, which effectively represents an unwounded monolayer and not the wound-healing assays described previously. The model therefore predicts that confluent I-PLs should be much more dynamic than I-FNs. We examined collective motion in confluent layers for all four of our previously described scenarios (Fig. 5, c and d; Fig. S5; Movies S6 and S7).

The first and most notable observation from the time-lapse movies from these experiments is that the I-PL cells show dramatically different dynamics than the other three cases (Movies S6 and S7). Where the MDCK II and I-FN cells show small random movements, the I-PL cells undergo large-scale, highly coordinated motion. We quantified these dynamics by measuring the intralayer velocity fields and found that the confluent I-PL cells had significantly larger average velocities (22 ± 1 μm/h) within the monolayer when compared with I-FN cells (10 ± 0.3 μm/h), II-FN cells (7.4 ± 0.3 μm/h), or II-PL cells (11.4 ± 0.3 μm/h) (Fig. 5, e and f; Fig. S5; Movies S6 and S7). We also used the velocity fields to compute the velocity-velocity spatial correlation (Fig. S5 g) (32). The spatial correlation functions for the I-FN, II-FN, and II-PL cells were nearly identical and showed a rapid decrease in correlation with distance. Effectively, these cells were not overly coordinated, with correlation lengths of only 1–2 cell diameters. However, the spatial correlation for the I-PL cells was significantly different and showed larger correlation over longer distances (Fig. S5 g). To further quantify the dynamics within the monolayers, we simulated the motion of tracer particles driven by the extracted velocity fields (Fig. 5, g and h; Movie S8). Overlays of these tracer particles onto the original movies also confirm that the extracted velocity fields are accurate. As is apparent in the movies, the I-PL cells migrate over much larger distances than the other cells, showing a fourfold increase in displacement over a 5 h period compared with the I-FN cells. Substrate coating did not strongly affect the MDCK II cells, with only a small increase in the particle displacements for II-PL compared with II-FN (Fig. S5, e and f).

As a further test of our model, we used blebbistatin and calyculin A to either inhibit myosin II activity or accentuate it, thereby either decreasing or increasing contractile stress (50, 51). Confluent layers of I-FN and I-PL cells were imaged for 2 h and were then treated with either 50 μM blebbistatin or 10 nM calyculin A. The average intralayer speed was measured pretreatment and for 2 h posttreatment. Pretreatment, the average intralayer speeds agreed with our previous measurements on untreated confluent layers. Interestingly, we found that blebbistatin treatment, which should decrease contractile stress, increased intralayer speed to 11.3 ± 0.7 μm/h for I-FN cells, whereas calyculin A had no effect (intralayer speed of 9.9 ± 0.4 μm/h) (Fig. 5 I; Fig. S6). However, for I-PL cells, blebbistatin decreased intralayer speed to 16.2 ± 0.6 μm/h and calyculin A increased intralayer speed to 27.9 ± 2.0 μm/h (Fig. 5 i; Fig. S6). A DMSO control showed no alteration to the intralayer speed. Although the I-FN results seem to be counter to the predictions of our model, we examined the dependence of intralayer speed on the contractile stress for isolated cell speeds of 25 μm/h (I-FN) and 12 μm/h (I-PL). The model showed nonmonotonic dependence of intralayer speed with respect to contractile stress for isolated cell speeds of 25 μm/h when the contractile stress varied from 0.1 to 0.3 nN/μm, which is consistent with our drug treatment data for I-FN (Fig. 5 j; Fig. S6). For isolated cell speed of 12 μm/h, the intralayer speed monotonically increases with contractile stress (Fig. 5 j), which agrees well with our drug treatment experiments on I-PL.

Discussion

Although the dynamics of collective migration have been studied extensively of late (e.g., (2, 13, 16, 18, 31, 32, 42, 52)), how single-cell behavior is harnessed to produce these coordinated motions has been largely ignored. Here, we show that it is possible to link isolated, single-cell behavior to epithelial dynamics; however, neither the speed of isolated single cells nor the presence of notorious leader cells correlated with the velocities of the collective. Instead, the biophysical feature of a single cell that most strongly correlated with the magnitude of collective motion was the intracellular contractile stress, a result anticipated by the model of Lee and Wolgemuth (25, 26, 27).

Our results also call into question the usefulness of drawing an analogy between epithelial monolayers and physical systems near a jamming transition. If this analogy is correct, then a potential reason that MDCK I cells move slower as a collective than when isolated on FN is that the collective is closer to the jamming transition. Then, by the same reason, MDCK I cells on PL should be further from this transition. However, we found that in the context of recent work on epithelial cell jamming (22), increases and not decreases in isolated cell speed should drive this system toward jamming; consequently, I-PL should move even slower than I-FNs during collective migration. The jamming and glass transition literature also does not explain why the I-PLs would move faster as a collective than they do when isolated.

Our experiments on single-cell migration of MDCK I and II cells on either FN or PL substrates showed that even though these cell types are closely related, they respond differently to these substrates. MDCK I cells migrated significantly faster on FN than on PL, whereas the speed of MDCK II cells was barely altered. One explanation for the difference is that PL decreases cell adhesion for MDCK cells. Spread area is typically an indicator of substrate adhesion strength (53). Therefore, the decrease in area of MDCK I cells on PL compared with FN is indicative of a decrease in adhesion. Why this decrease in adhesion leads to larger traction forces is not clear. Although MDCK II cells did not show a significant decrease in spread area on PL, the large reduction in traction force may be attributable to a decrease in adhesion, which would also explain why II-PL wound-healing assays showed a retraction of the wound border. It is not clear why MDCK I and II cells would respond differently to FN and PL. Regardless of the actual changes in adhesion that are induced by FN and PL, our data conclusively rules out cell speed as the driving force behind wound healing. Because eukaryotic cells crawl by contracting, only a small fraction of the contractile stress is used to generate the propulsive force that pushes the cell across the substrate. Some recent models for epithelial dynamics treat the collective as a population of discrete, point-like cells driven by a propulsive force (19, 20), and therefore ignore the substantial contractile stresses inside the cells. In these models, collisions inhibit the motility of the individual, consequently causing the velocities in the collective to be substantially slower than the discrete cells would be in isolation. Our results provide evidence that these models are lacking crucial components of the driving physics.

We showed here that traction stresses from intracellular contraction are larger on PL coated slides than on FN coated slides. Our mathematical model includes both isolated cell speed and intracellular contraction. As shown in Fig. 5, both of these factors influence the speed of collective motions. Our model supports that intracellular contraction can be a dominant factor in collective movements, and that because of these contractile forces, collective motions can be faster than isolated cell speed. It is possible that other factors such as cell division or contact repulsion could also lead to more rapid motions in the collective. However, there was no noticeable difference in growth rates on PL compared with FN. In addition, because the spread area of MDCK I cells in the monolayers were nearly identical between the two substrates, this suggests that contact-related effects should also be approximately equal. Therefore, although we cannot rule out other possible mechanisms, our results show that intracellular contractile forces can explain the results presented here.

Another important consequence of this result is that it draws into question the use of wound-healing assays as a general measure of cell motility. In morphogenesis and early stage cancer invasion and metastasis, it remains unknown how migratory cell populations emerge from homogenous, seemingly stationary, multicellular systems (15, 54). Wound-healing assays have been a ubiquitous technique for investigating this question (3, 6, 55, 56, 57), mostly due to the simplicity of the assay and the ease of analysis. However, the principal assumption made when using these assays is that wound closure rates correlate with the migratory potential of the cells. Our results raise two issues. First, although wound-healing assays may be informative for cancers and developmental processes where collective migration is involved, they should not be used to study single-cell processes such as the metastases from leukemias, lymphomas, and most solid stromal tumors (54). Likewise, single-cell experiments are not informative for processes that involve collective migrations. Second, we also found that simple modifications of the interaction between the cell and the substrate can lead to drastically different behavior at the collective level, which suggests that conclusions drawn from in vitro assays that do not exactly reproduce the in vivo environment could be vastly misleading. However grim that consequence may be for in vitro experiments, our work has identified a key aspect of the biophysics of collective migration, which should provide some guidance as we stream, crawl, branch, and sprout our way toward a better understanding of coordinated cellular movements.

Author Contributions

D.K.V, A.E.H., and C.W.W. designed the research. D.K.V. and A.E.H. performed the research. D.K.V. analyzed the data. D.K.V. and C.W.W. performed simulations and wrote the article.

Editor: Stanislav Shvartsman.

Supporting Material

Movie S1. The Motility of Single MDCK Type I Cells on Fibronectin and Poly-L-Lysine

DIC images were acquired every 3 min using a 20× (0.8 NA) air objective. These movies span 4 h. Fibronectin appears in the left panel and poly-L-lysine appears in the right panel.

Movie S2. The Motility of Single MDCK Type II Cells on Fibronectin and Poly-L-Lysine

DIC images were acquired every 3 min using a 20× (0.8 NA) air objective. These movies span 4 h. Fibronectin appears in the left panel and poly-L-lysine appears in the right panel.

Movie S3. Collective Migration of MDCK Type I Cells during Wound-Healing Assays on Fibronectin and Poly-L-Lysine

DIC images were acquired every 5 min using a 20× (0.8 NA) air objective. The total movie duration is 4 h. Flow fields (green arrows) were measured using the following parameters: BoxSize = 10, BlurSize = 13, BlurSTD = 4, SmoothSize = 61, SmoothSTD = 30, and ArrowSize = 61. Fibronectin appears in the left panel and poly-L-lysine appears in the right panel.

Movie S4. Collective Migration of MDCK Type II Cells during Wound-Healing Assays on Fibronectin and Poly-L-Lysine

DIC images were acquired every 5 min using a 20× (0.8 NA) air objective. The total movie duration is 4 h. Flow fields (green arrows) were measured using the same parameters as in Movie S3. Fibronectin appears in the left panel and poly-L-lysine appears in the right panel.

Movie S5. Simulation of the Collective Migration Model for a Confluent Epithelium

The simulation uses the model parameters given in Table S1, with f_d = 0.6 nN/μm and V₀ = 10 μm/h.

Movie S6. Collective Migration of MDCK Type I Cells in Confluent Monolayers on Fibronectin and Poly-L-Lysine

DIC images were acquired every 5 min using a 20× (0.8 NA) air objective. The total movie duration is 5 h. Green arrows represent the extracted flow fields. For fibronectin-treated surfaces the parameters were set as in Movie S3. Due to the dramatic increase in speed on poly-L-lysine, we increased BlurSize and BlurSTD to 61 and 7, respectively. Fibronectin appears in the left panel and poly-L-lysine appears in the right panel.

Movie S7. Collective Migration of MDCK Type II Cells in Confluent Monolayers on Fibronectin and Poly-L-Lysine

DIC images were acquired every 5 min using a 20× (0.8 NA) air objective. The total movie duration is 5 h. Flow fields (green arrows) were measured using the same parameters as in Movie S3. Fibronectin appears in the left panel and poly-L-lysine appears in the right panel.

Movie S8. Recreation of Cell Movements using Extracted Velocities

Using the velocities measured in a confluent monolayer of MDCK type I cells on poly-L-lysine (Movie S6), we simulated the motion of tracer particles (red circles) and overlaid the positions onto the original movie. The movements of these particles follow the motions of the cells.