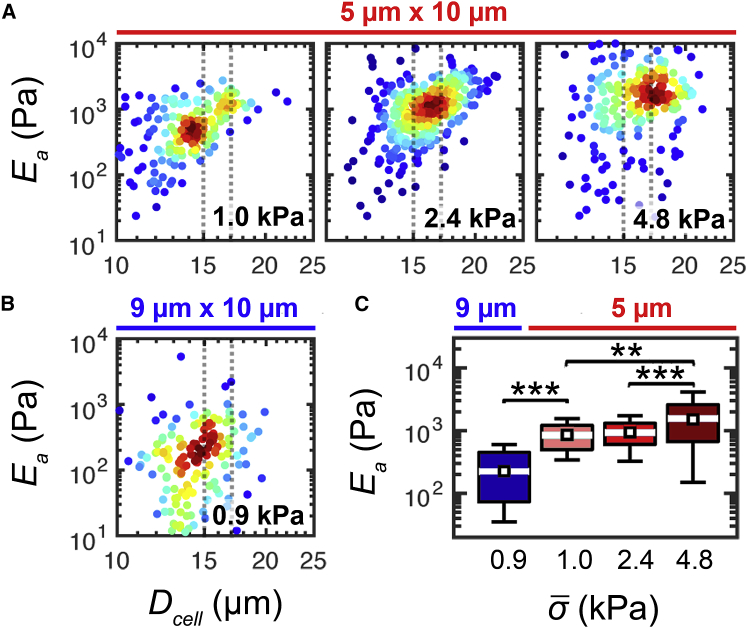
Figure 4.

Mechanotype of HL-60 cells depends on applied pressure and cell/pore-size ratio. (A) Density scatter plots show apparent elastic modulus, E_a, as a function of cell size. The cell diameter, D_cell, is measured in the microfluidic channel before the cell enters the constriction. Data represent the deformation response for HL-60 cells that are driven to deform through 5 × 10 μm constrictions with increasing applied pressure. The calibrated applied stress is shown on the bottom right corner of each plot. Dots represent single-cell data. Cell size, measured by q-DC, increases with applied pressure, as there is a higher probability that larger cells will transit at higher pressures; at lower pressures, larger cells have a higher probability of occluding constrictions. To compare data sets, we bin cells by the median cell diameter, as indicated by the gray dashed lines; the resultant size-binned data are shown in the boxplots in (C). (B) Density scatter plot illustrating the elastic modulus, E_a, as a function of cell size for HL-60 cells deforming through 9 × 10 μm constrictions. (C) Boxplots show the size-gated distributions of E_a for HL-60 cells with D_cell = 16 ± 1 μm. Cells are subject to varying applied stresses, $\overline{\sigma }$, and constriction geometries: white lines represent the median, boxes represent the interquartile ranges, whiskers represent the 10th and 90th percentiles, and white squares represent the bootstrapped median. N > 200 for each cell type. Statistical significance is determined using the Mann-Whitney U test: ^∗∗p < 0.01, ^∗∗∗p < 0.001. To see this figure in color, go online.