Fig. 4.

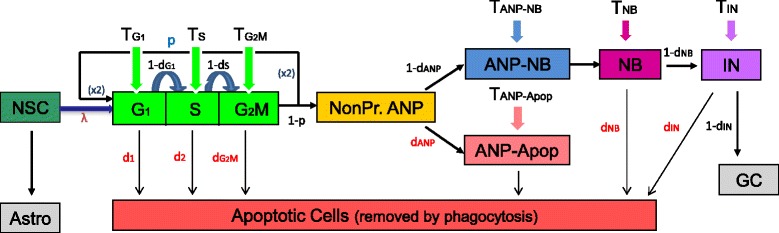
Hierarchical structure of the neurogenic cascade modeled by the Multitype Bellman-Harris branching process with different cell types as different compartments. Consider a collection of particles of I types, which proliferate according to the following rules: At time t=0, an ancestor particle of type i is born, which lives for a random time τ with cumulative distribution function (cdf) T _i and upon death, it produces a random number of progeny of all types, described by a vector (X ₁,...,X _I) with multivariate probability generating function h _i(s ₁,...,s _I) At time t=τ, each first-generation progeny particle of type j lives for a random time with cumulative distribution function (cdf) T _j and upon death, produces a random number of progeny of all types, described by vector of multivariate pgf h _j(s ₁,...,s _I), independently of other progeny particles. The cycle of life, death and progeny production is repeated indefinitely by each generation of particles. ʎ= intensity of influx of new ANPs from NSCs, X ₂ = cell doubling rate, D _i= cell death rate of the cell i, p = renewal probability of ANPs, T _i= duration time of cell in stage i. G1, S, G2M = stages of cell cycle. NonPr ANP = non-proliferating ANP. Astro = astrocyte