Abstract
We present *K-means clustering algorithm and source code by expanding statistical clustering methods applied in https://ssrn.com/abstract=2802753 to quantitative finance. *K-means is statistically deterministic without specifying initial centers, etc. We apply *K-means to extracting cancer signatures from genome data without using nonnegative matrix factorization (NMF). *K-means’ computational cost is a fraction of NMF’s. Using 1389 published samples for 14 cancer types, we find that 3 cancers (liver cancer, lung cancer and renal cell carcinoma) stand out and do not have cluster-like structures. Two clusters have especially high within-cluster correlations with 11 other cancers indicating common underlying structures. Our approach opens a novel avenue for studying such structures. *K-means is universal and can be applied in other fields. We discuss some potential applications in quantitative finance.
Keywords: Clustering, K-means, Nonnegative matrix factorization, Somatic mutation, Cancer signatures, Genome, eRank, Machine learning, Sample, Source code
1. Introduction and summary
Every time we can learn something new about cancer, the motivation goes without saying. Cancer is different. Unlike other diseases, it is not caused by “mechanical” breakdowns, biochemical imbalances, etc. Instead, cancer occurs at the DNA level via somatic alterations in the genome structure. A common type of somatic mutations found in cancer is due to single nucleotide variations (SNVs) or alterations to single bases in the genome, which accumulate through the lifespan of the cancer via imperfect DNA replication during cell division or spontaneous cytosine deamination [1], [2], or due to exposures to chemical insults or ultraviolet radiation [3], [4], etc. These mutational processes leave a footprint in the cancer genome characterized by distinctive alteration patterns or mutational signatures.
If we can identify all underlying signatures, this could greatly facilitate progress in understanding the origins of cancer and its development. Therapeutically, if there are common underlying structures across different cancer types, then a therapeutic for one cancer type might be applicable to other cancers, which would be a great news.2 However, it all boils down to the question of usefulness, i.e., is there a small enough number of cancer signatures underlying all (100+) known cancer types, or is this number too large to be meaningful or useful? Indeed, there are only 96 SNVs,3 so we cannot have more than 96 signatures.4 Even if the number of true underlying signatures is, say, of order 50, it is unclear whether they would be useful, especially within practical applications. On the other hand, if there are only a dozen or so underlying signatures, then we could hope for an order of magnitude simplification.
To identify mutational signatures, one analyzes SNV patterns in a cohort of DNA sequenced whole cancer genomes. The data is organized into a matrix Gis, where the rows correspond to the N = 96 mutation categories, the columns correspond to d samples, and each element is a nonnegative occurrence count of a given mutation category in a given sample. Currently, the commonly accepted method for extracting cancer signatures from Gis [5] is via nonnegative matrix factorization (NMF) [6], [7]. Under NMF the matrix G is approximated via G ≈ W H, where WiA is an N × K matrix, HAs is a K × d matrix, and both W and H are nonnegative. The appeal of NMF is its biologic interpretation whereby the K columns of the matrix W are interpreted as the weights with which the K cancer signatures contribute into the N = 96 mutation categories, and the columns of the matrix H are interpreted as the exposures to the K signatures in each sample. The price to pay for this is that NMF, which is an iterative procedure, is computationally costly and depending on the number of samples d it can take days or even weeks to run it. Furthermore, it does not automatically fix the number of signatures K, which must be either guessed or obtained via trial and error, thereby further adding to the computational cost.5
Some of the aforesaid issues were recently addressed in [8], to wit: (i) by aggregating samples by cancer types, we can greatly improve stability and reduce the number of signatures;6 (ii) by identifying and factoring out the somatic mutational noise, or the “overall” mode (this is the “de-noising” procedure of [8]), we can further greatly improve stability and, as a bonus, reduce computational cost; and (iii) the number of signatures can be fixed borrowing the methods from statistical risk models [9] in quantitative finance, by computing the effective rank (or eRank) [10] for the correlation matrix Ψij calculated across cancer types or samples (see below). All this yields substantial improvements [8].
In this paper we push this program to yet another level. The basic idea here is quite simple (but, as it turns out, nontrivial to implement – see below). We wish to apply clustering techniques to the problem of extracting cancer signatures. In fact, we argue in Section 2 that NMF is, to a degree, “clustering in disguise”. This is for two main reasons. The prosaic reason is that NMF, being a nondeterministic algorithm, requires averaging over many local optima it produces. However, each run generally produces a weights matrix WiA with columns (i.e., signatures) not aligned with those in other runs. Aligning or matching the signatures across different runs (before averaging over them) is typically achieved via nondeterministic clustering such as k-means. So, not only is clustering utilized at some layer, the result, even after averaging, generally is both noisy7 and nondeterministic! I.e., if this computationally costly procedure (which includes averaging) is run again and again on the same data, generally it will yield different looking cancer signatures every time!
The second, not-so-prosaic reason is that, while NMF generically does not produce exactly null weights, it does produce low weights, such that they are within error bars. For all practical purposes we might as well set such weights to zero. NMF requires nonnegative weights. However, we could as reasonably require that the weights should be, say, outside error bars (e.g., above one standard deviation – this would render the algorithm highly recursive and potentially unstable or computationally too costly) or above some minimum threshold (which would still further complicated as-is complicated NMF), or else the non-compliant weights are set to zero. As we increase this minimum threshold, the matrix WiA will start to have more and more zeros. It may not exactly have a binary cluster-like structure, but it may at least have some substructures that are cluster-like. It then begs the question: are there cluster-like (sub)structures present in WiA or, generally, in cancer signatures?
To answer this question, we can apply clustering methods directly to the matrix Gis, or, more, precisely, to its de-noised version (see below) [8]. The naïve, brute-force approach where one would simply cluster Gis or does not work for a variety of reasons, some being more nontrivial or subtle than others. Thus, e.g., as discussed in [8], the counts Gis have skewed, long-tailed distributions and one should work with log-counts, or, more precisely, their de-noised versions. This applies to clustering as well. Further, following a discussion in [11] in the context of quantitative trading, it would be suboptimal to cluster de-noised log-counts. Instead, it pays to cluster their normalized variants (see Section 2 hereof). However, taking care of such subtleties does not alleviate one big problem: nondeterminism!8 If we run a vanilla nondeterministic algorithm such as k-means on the data however massaged with whatever bells and whistles, we will get random-looking disparate results every time we run k-means with no stability in sight. We need to address nondeterminism!
Our solution to the problem is what we term *K-means. The idea behind *K-means, which essentially achieves determinism statistically, is simple. Suppose we have an N × d matrix Xis, i.e., we have N d-vectors Xi. If we run k-means with the input number of clusters K but initially unspecified centers, every run will generally produce a new local optimum. *K-means reduces and in fact essentially eliminates this indeterminism via two levels. At level 1 it takes clusterings obtained via M independent runs or samplings. Each sampling produces a binary N × K matrix ΩiA, whose element equals 1 if Xi belongs to the cluster labeled by A, and 0 otherwise. The aggregation algorithm and the source code therefor are given in [11]. This aggregation – for the same reasons as in NMF (see above) – involves aligning clusters across the M runs, which is achieved via k-means, and so the result is nondeterministic. However, by aggregating a large number M of samplings, the degree of nondeterminism is greatly reduced. The “catch” is that sometimes this aggregation yields a clustering with K′ < K clusters, but this does not pose an issue. Thus, at level 2, we take a large number P of such aggregations (each based on M samplings). The occurrence counts of aggregated clusterings are not uniform but typically have a (sharply) peaked distribution around a few (or manageable) number of aggregated clusterings. So this way we can pinpoint the “ultimate” clustering, which is simply the aggregated clustering with the highest occurrence count. This is the gist of *K-means and it works well for genome data.
So, we apply *K-mean to the same genome data as in [8] consisting of 1389 (published) samples across 14 cancer types (see below). Our target number of clusters is 7, which was obtained in [8] using the eRank based algorithm (see above). We aggregated 1000 samplings into clusterings, and we constructed 150,000 such aggregated clusterings (i.e., we ran 150 million k-means instances). We indeed found the “ultimate” clustering with 7 clusters. Once the clustering is fixed, it turns out that within-cluster weights can be computed via linear regressions (with some bells and whistles) and the weights are automatically positive. That is, we do not need NMF at all! Once we have clusters and weights, we can study reconstruction accuracy and within-cluster correlations between the underlying data and the fitted data that the cluster model produces.
We find that clustering works well for 10 out the 14 cancer types we study. The cancer types for which clustering does not appear to work all that well are Liver Cancer, Lung Cancer, and Renal Cell Carcinoma. Also, above 80% within-cluster correlations arise for 5 out of 7 clusters. Furthermore, remarkably, one cluster has high within-cluster correlations for 9 cancer types, and another cluster for 6 cancer types. These appear to be the leading clusters. Together they have high within-cluster correlations in 11 out of 14 cancer types. So what does all this mean?
Additional insight is provided by looking at the within-cluster correlations between signatures Sig1 through Sig7 extracted in [8] and our clusters. High within-cluster correlations arise for Sig1, Sig2, Sig4 and Sig7, which are precisely the signatures with “peaks” (or “spikes” – “tall mountain landscapes”), whereas Sig3, Sig5 and Sig6 do not have such “peaks” (“flat” or “rolling hills landscapes”); see Figs. 14 through 20 of [8]. The latter 3 signatures simply do not have cluster-like structures. Looking at Fig. 21 in [8], it becomes evident why clustering does not work well for Liver Cancer – it has a whopping 96% contribution from Sig5! Similarly, Renal Cell Carcinoma has a 70% contribution from Sig6. Lung Cancer is dominated by Sig3, hence no cluster-like structure. So, Liver Cancer, Lung Cancer and Renal Cell Carcinoma have little in common with other cancers (and each other)! However, 11 other cancers, to wit, B Cell Lymphoma, Bone Cancer, Brain Lower Grade Glioma, Breast Cancer, Chronic Lymphocytic Leukemia, Esophageal Cancer, Gastric Cancer, Medulloblastoma, Ovarian Cancer, Pancreatic Cancer and Prostate Cancer, have 5 (with 2 leading) cluster structures substantially embedded in them.
In Section 2 we (i) discuss why applying clustering algorithms to extracting cancer signatures makes sense, (ii) argue that NMF, to a degree, is “clustering in disguise”, and (iii) give the machinery for building cluster models via *K-means, including various details such as what to cluster, how to fix the number of clusters, etc. In Section 3 we discuss (i) cancer genome data we use, (ii) our application of *K-means to it, and (iii) the interpretation of our empirical results. Section 4 contains some concluding remarks, including a discussion of potential applications of *K-means in quantitative finance, where we outline some concrete problems where *K-means can be useful. Appendix A contains R source code for *K-means and cluster models.
2. Cluster models
The chief objective of this paper is to introduce a novel approach to identifying cancer signatures using clustering methods. In fact, as we discuss below in detail, our approach is more than just clustering. Indeed, it is evident from the get-go that blindly using nondeterministic clustering algorithms,9 which typically produce (unmanageably) large numbers of local optima, would introduce great variability into the resultant cancer signatures.10 On the other hand, deterministic algorithms such as agglomerative hierarchical clustering11 typically are (substantially) slower and require essentially “guessing” the initial clustering,12 which in practical applications13 can often turn out to be suboptimal. So, both to motivate and explain our new approach employing clustering methods, we first – so to speak – “break down” the NMF approach and argue that it is in fact a clustering method in disguise!
2.1. “Breaking down” NMF
The current “lore” – the commonly accepted method for extracting K cancer signatures from the occurrence counts matrix Gis (see above) [5] – is via nonnegative matrix factorization (NMF) [6], [7]. Under NMF the matrix G is approximated via G ≈ W H, where WiA is an N × K matrix of weights, HAs is a K × d matrix of exposures, and both W and H are nonnegative. However, not only is the number of signatures K not fixed via NMF (and must be either guessed or obtained via trial and error), NMF too is a nondeterministic algorithm and typically produces a large number of local optima. So, in practice one has no choice but to execute a large number NS of NMF runs – which we refer to as samplings – and then somehow extract cancer signatures from these samplings. Absent a guess for what K should be, one executes NS samplings for a range of values of K (say, Kmin ≤ K ≤ Kmax, where Kmin and Kmax are basically guessed based on some reasonable intuitive considerations), for each K extracts cancer signatures (see below), and then picks K and the corresponding signatures with the best overall fit into the underlying matrix G. For a given K, different samplings generally produce different weights matrices W. So, to extract a single matrix W for each value of K one averages over the samplings. However, before averaging, one must match the K cancer signatures across different samplings – indeed, in a given sampling X the columns in the matrix WiA are not necessarily aligned with the columns in the matrix WiA in a different sampling Y. To align the columns in the matrices W across the NS samplings, once often uses a clustering algorithm such as k-means. However, since k-means is nondeterministic, such alignment of the W columns is not guaranteed to – and in fact does not – produce a unique answer. Here one can try to run multiple samplings of k-means for this alignment and aggregate them, albeit such aggregation itself would require another level of alignment (with its own nondeterministic clustering such as k-means).14 And one can do this ad infinitum. In practice, one must break the chain at some level of alignment, either ad hoc (essentially by heuristically observing sufficient stability and “convergence”) or via using a deterministic algorithm (see footnote14). Either way, invariably all this introduces (overtly or covertly) systematic and statistical errors into the resultant cancer signatures and often it is unclear if they are meaningful without invoking some kind empirical biologic “experience” or “intuition” (often based on already well-known effects of, e.g., exposure to various well-understood carcinogens such as tobacco, ultraviolet radiation, aflatoxin, etc.). At the end of the day it all boils down to how useful – or predictive – the resultant method of extracting cancer signatures is, including signature stability. With NMF, the answer is not at all evident…
2.2. Clustering in disguise?
So, in practice, under the hood, NMF already uses clustering methods. However, it goes deeper than that. While NMF generically does not produce vanishing weights for a given signature, some weights are (much) smaller than others. E.g., often one has several “peaks” with high concentration of weights, with the rest of the mutation categories having relatively low weights. In fact, many weights can even be within the (statistical plus systematic) error bars.15 Such weights can for all practical purposes be set to zero. In fact, we can take this further and ask whether proliferation of low weights adds any explanatory power. One way to address this is to run NMF with an additional constraint that the weights (obtained via averaging – see above) should be higher than either (i) some multiple of the corresponding error bars16 or (ii) some preset fixed minimum weight. This certainly sounds reasonable, so why is this not done in practice? A prosaic answer appears to be that this would complicate the already nontrivial NMF algorithm even further, require additional coding and computation resources, etc. However, arguendo, let us assume that we require, say, that the weights be higher than a preset fixed minimum weight or else the weights are set to zero. As we increase , the so-modified NMF would produce more and more zeros. This does not mean that the resulting matrix WiA would have a binary cluster structure, i.e., that , where δAB is a Kronecker delta and G : {1, …, N} ↦ {1, …, K} is a map from N = 96 mutation categories to K clusters. Put another way, this does not mean that in the resulting matrix WiA for a given i (i.e., mutation category) we would have a nonzero element for one and only one value of A (i.e., signature). However, as we gradually increase , generally the matrix WiA is expected to look more and more like having a binary cluster structure, albeit with some “overlapping” signatures (i.e., such that in a given pair of signatures there are nonzero weights for one or more mutations). We can achieve a binary structure via a number of ways. Thus, a rudimentary algorithm would be to take the matrix WiA (equally successfully before or after achieving some zeros in it via nonzero ) and for a given value of i set all weights WiA to zero except in the signature A for which WiA = max(WiA|A = 1, …, K). Note that this might result in some empty signatures (clusters), i.e., signatures with WiA = 0 for all values of i. This can be dealt with by (i) ether simply dropping such signatures altogether and having fewer K′ < K signatures (binary clusters) at the end, or (ii) augmenting the algorithm to avoid empty clusters, which can be done in a number of ways we will not delve into here. The bottom line is that NMF essentially can be made into a clustering algorithm by reasonably modifying it, including via getting rid of ubiquitous and not-too-informative low weights. However, the downside would be an even more contrived algorithm, so this is not what we are suggesting here. Instead, we are observing that clustering is already intertwined in NMF and the question is whether we can simplify things by employing clustering methods directly.
2.3. Making clustering work
Happily, the answer is yes. Not only can we have much simpler and apparently more stable clustering algorithms, but they are also computationally much less costly than NMF. As mentioned above, the biggest issue with using popular nondeterministic clustering algorithms such as k-means17 is that they produce a large number of local optima. For definiteness in the remainder of this paper we will focus on k-means, albeit the methods described herein are general and can be applied to other such algorithms. Fortunately, this very issue has already been addressed in [11] in the context of constructing statistical industry classifications (i.e., clustering models for stocks) for quantitative trading, so here we simply borrow therefrom and further expand and adapt that approach to cancer signatures.
2.3.1. K-means
A popular clustering algorithm is k-means [12], [13], [14], [15], [16], [17], [18]. The basic idea behind k-means is to partition N observations into K clusters such that each observation belongs to the cluster with the nearest mean. Each of the N observations is actually a d-vector, so we have an N × d matrix Xis, i = 1, …, N, s = 1, …, d. Let Ca be the K clusters, Ca = {i|i ∈ Ca}, a = 1, …, K. Then k-means attempts to minimize18
| (1) |
where
| (2) |
are the cluster centers (i.e., cross-sectional means),19 and na = |Ca| is the number of elements in the cluster Ca. In (1) the measure of “closeness” is chosen to be the Euclidean distance between points in Rd, albeit other measures are possible.
One “drawback” of k-means is that it is not a deterministic algorithm. Generically, there are copious local minima of g in (1) and the algorithm only guarantees that it will converge to a local minimum, not the global one. Being an iterative algorithm, unless the initial centers are preset, k-means starts with a random set of the centers Yas at the initial iteration and converges to a different local minimum in each run. There is no magic bullet here: in practical applications, typically, trying to “guess” the initial centers is not any easier than “guessing” where, e.g., the global minimum is. So, what is one to do? One possibility is to simply live with the fact that every run produces a different answer. In fact, this is acceptable in many applications. However, in the context of extracting cancer signatures this would result in an exercise in futility. We need a way to eliminate or greatly reduce indeterminism.
2.3.2. Aggregating clusterings
The idea is simple. What if we aggregate different clusterings from multiple runs – which we refer to as samplings – into one? The question is how. Suppose we have M runs (M ≫ 1). Each run produces a clustering with K clusters. Let , i = 1, …, N, a = 1, …, K (here Gr : {1, …, N} ↦ {1, …, K} is the map between – in our case – the mutation categories and the clusters),20 be the binary matrix from each run labeled by r = 1, …, M, which is a convenient way (for our purposes here) of encoding the information about the corresponding clustering; thus, each row of contains only one element equal 1 (others are zero), and (i.e., column sums) is nothing but the number of mutations belonging to the cluster labeled by a (note that ). Here we are assuming that somehow we know how to properly order (i.e., align) the K clusters from each run. This is a nontrivial assumption, which we will come back to momentarily. However, assuming, for a second, that we know how to do this, we can aggregate the binary matrices into a single matrix . Now, this matrix does not look like a binary clustering matrix. Instead, it is a matrix of occurrence counts, i.e., it counts how many times a given mutation was assigned to a given cluster in the process of M samplings. What we need to construct is a map G such that one and only one mutation belongs to each of the K clusters. The simplest criterion is to map a given mutation to the cluster in which is maximal, i.e., where said mutation occurs most frequently. A caveat is that there may be more than one such clusters. A simple criterion to resolve such an ambiguity is to assign said mutation to the cluster with most cumulative occurrences (i.e., we assign said mutation to the cluster with the largest ). Further, in the unlikely event that there is still an ambiguity, we can try to do more complicated things, or we can simply assign such a mutation to the cluster with the lowest value of the index a – typically, there is so much noise in the system that dwelling on such minutiae simply does not pay off.
However, we still need to tie up a loose end, to wit, our assumption that the clusters from different runs were somehow all aligned. In practice each run produces K clusters, but (i) they are not the same clusters and there is no foolproof way of mapping them, especially when we have a large number of runs; and (ii) even if the clusters were the same or similar, they would not be ordered, i.e., the clusters from one run generally would be in a different order than the clusters from another run.
So, we need a way to “match” clusters from different samplings. Again, there is no magic bullet here either. We can do a lot of complicated and contrived things with not much to show for it at the end. A simple pragmatic solution is to use k-means to align the clusters from different runs. Each run labeled by r = 1, …, M, among other things, produces a set of cluster centers . We can “bootstrap” them by row into a (KM) × d matrix , where takes values . We can now cluster into K clusters via k-means. This will map each value of to {1, …, K} thereby mapping the K clusters from each of the M runs to {1, …, K}. So, this way we can align all clusters. The “catch” is that there is no guarantee that each of the K clusters from each of the M runs will be uniquely mapped to one value in {1, …, K}, i.e., we may have some empty clusters at the end of the day. However, this is fine, we can simply drop such empty clusters and aggregate (via the above procedure) the smaller number of K′ < K clusters. I.e., at the end we will end up with a clustering with K′ clusters, which might be fewer than the target number of clusters K. This is not necessarily a bad thing. The dropped clusters might have been redundant in the first place. Another evident “catch” is that even the number of resulting clusters K′ is not deterministic. If we run this algorithm multiple times, we will get varying values of K′. Malicious circle?
2.3.3. Fixing the “ultimate” clustering
Not really! There is one other trick up our sleeves we can use to fix the “ultimate” clustering thereby rendering our approach essentially deterministic. The idea above is to aggregate a large enough number M of samplings. Each aggregation produces a clustering with some K′ ≤ K clusters, and this K′ varies from aggregation to aggregation. However, what if we take a large number P of aggregations (each based on M samplings)? Typically there will be a relatively large number of different clusterings we get this way. However, assuming some degree of stability in the data, this number is much smaller than the number of a priori different local minima we would obtain by running the vanilla k-means algorithm. What is even better, the occurrence counts of aggregated clusterings are not uniform but typically have a (sharply) peaked distribution around a few (or manageable) number of aggregated clusterings. In fact, as we will see below, in our empirical genome data we are able to pinpoint the “ultimate” clustering! So, to recap, what we have done here is this. There are myriad clusterings we can get via vanilla k-means with little to no guidance as to which one to pick.21 We have reduced this proliferation by aggregating a large number of such clusterings into our aggregated clusterings. We then further zoom onto a few or even a unique clustering we consider to be the likely “ultimate” clustering by examining the occurrence counts of such aggregated clusterings, which turns out to have a (sharply) peaked distribution. Since vanilla k-means is a relatively fast-converging algorithm, each aggregation is not computationally taxing and running a large number of aggregations is nowhere as time consuming as running a similar number (or even a fraction thereof) of NMF computations (see below).
2.4. What to cluster?
So, now that we know how to make clustering work, we need to decide what to cluster, i.e., what to take as our matrix Xis in (1). The naïve choice Xis = Gis is suboptimal for multiple reasons (as discussed in [8]).
First, the elements of the matrix Gis are populated by nonnegative occurrence counts. Nonnegative quantities with large numbers of samples tend to have skewed distributions with long tails at higher values. I.e., such distributions are not normal but (in many cases) roughly log-normal. One simple way to deal with this is to identify Xis with a (natural) logarithm of Gis (instead of Gis itself). A minor hiccup here is that some elements of Gis can be 0. We can do a lot of complicated and even convoluted things to deal with this issue. Here, as in [8], we will follow a pragmatic approach and do something simple instead – there is so much noise in the data that doing convoluted things simply does not pay off. So, as the first cut, we can take
| (3) |
This takes care of the Gis = 0 cases; for Gis ≫ 1 we have Ris ≈ ln(Gis), as desired.
Second, the detailed empirical analysis of [8] uncovered what is termed therein the “overall” mode22 unequivocally present in the occurrence count data. This “overall” mode is interpreted as somatic mutational noise unrelated to (and in fact obscuring) the true underlying cancer signatures and must therefore be factored out somehow. Here is a simple way to understand the “overall” mode. Let the correlation matrix Ψij = Cor(Xis, Xjs), where Cor(·, ·) is serial correlation.23 I.e., Ψij = Cij/σiσj, where are variances, and the serial covariance matrix24
| (4) |
where are serially demeaned, while the means . The average pair-wise correlation between different mutation categories is nonzero and is in fact high for most cancer types we study. This is the aforementioned somatic mutational noise that must be factored out. If we aggregate samples by cancer types (see below) and compute the correlation matrix Ψij for the so-aggregated data (across the n = 14 cancer types we study – see below),25 the average correlation ρ is over whopping 96%. Another way of thinking about this is that the occurrence counts in different samples (or cancer types, if we aggregate samples by cancer types) are not normalized uniformly across all samples (cancer types). Therefore, running NMF, a clustering or any other signature-extraction algorithm on the vanilla matrix Gis (or its “log” Xis defined in (3)) would amount to mixing apples with oranges thereby obscuring the true underlying cancer signatures.
Following [8], factoring out the “overall” mode (or “de-noising” the matrix Gis) therefore most simply amount to cross-sectional (i.e., across the 96 mutation categories) demeaning of the matrix Xis. I.e., instead of Xis we use , which is obtained from Xis by demeaning its columns:26
| (5) |
We should note that using instead of Xis in (1) does not affect clustering. Indeed, g in (1) is invariant under the transformations of the form Xis → Xis + Δs, where Δs is an arbitrary d-vector, as thereunder we also have Yas → Yas + Δs, so Xis − Yas is unchanged. In fact, this is good: this means that de-noising does not introduce any additional errors into clustering itself. However, the actual weights in the matrix WiA are affected by de-noising. We discuss the algorithm for fixing WiA below. However, we need one more ingredient before we get to determining the weights, and with this additional ingredient de-noising does affect clustering.
2.4.1. Normalizing log-counts
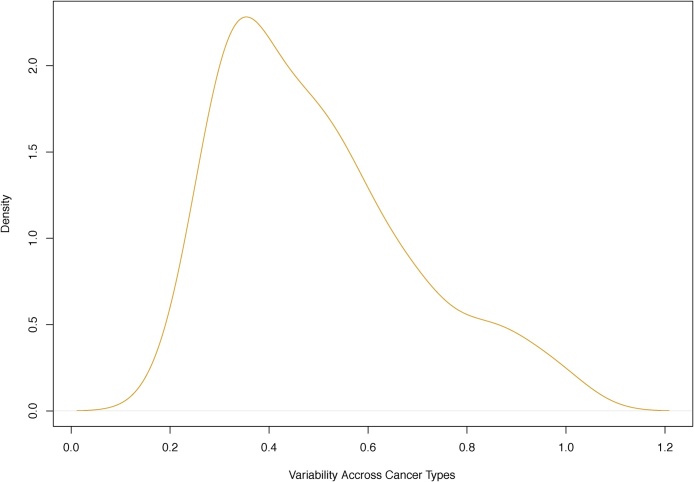
As was discussed in [11], clustering Xis (or equivalently ) would be suboptimal.27 The issue is this. Let be serial standard deviations, i.e., , where, as above, Cov(·, ·) is serial covariance. Here we assume that samples are aggregated by cancer types, so s = 1, …, d with d = n = 14. Now, are not cross-sectionally uniform and vary substantially across mutation categories. The density of is depicted in Fig. 1 and is skewed (tailed). The summary of reads:28 Min = 0.2196, 1st Qu. = 0.3409, Median = 0.4596, Mean = 0.4984, 3rd Qu. = 0.6060, Max = 1.0010, SD = 0.1917, MAD = 0.1859, Skewness = 0.8498. If we simply cluster , this variability in will not be accounted for.
Fig. 1.
Horizontal axis: serial standard deviation for N = 96 mutation categories (i = 1, …, N) of cross-sectionally demeaned log-counts across n = 14 cancer types (for samples aggregated by cancer types, so s = 1, …, d, d = n). Vertical axis: density using R function density(). See Section 2.4.1 for details.
A simple solution is to cluster normalized demeaned log-counts instead of . This way we factor out the nonuniform (and skewed) standard deviation out of the log-counts. Note that now de-noising does make a difference in clustering. Indeed, if we use (recall that ) instead of in (1) and (2), the quantity g (and also clusterings) will be different.
2.5. Fixing cluster number
Now that we know what to cluster (to wit, ) and how to get to the “unique” clustering, we need to figure out how to fix the (target) number of clusters K, which is one of the inputs in our algorithm above.29 In [8] it was argued that in the context of cancer signatures their number can be fixed by building a statistical factor model [9], i.e., the number of signatures is simply the number of statistical factors.30 So, by the same token, here we identify the (target) number of clusters in our clustering algorithm with the number of statistical factors fixed via the method of [9].
2.5.1. Effective rank
So, following [9], [8], we set31
| (6) |
Here eRank(Z) is the effective rank [10] of a symmetric semi-positive-definite (which suffices for our purposes here) matrix Z. It is defined as
| (7)(8)(9) |
where λ(a) are the L positive eigenvalues of Z, and H has the meaning of the (Shannon a.k.a. spectral) entropy [34], [35]. Let us emphasize that in (6) the matrix Ψij is computed based on the demeaned log-counts32 .
The meaning of eRank(Ψij) is that it is a measure of the effective dimensionality of the matrix Ψij, which is not necessarily the same as the number L of its positive eigenvalues, but often is lower. This is due to the fact that many d-vectors can be serially highly correlated (which manifests itself by a large gap in the eigenvalues) thereby further reducing the effective dimensionality of the correlation matrix.
2.6. How to compute weights?
The one remaining thing to accomplish is to figure out how to compute the weights WiA. Happily, in the context of clustering we have significant simplifications compared with NMF and computing the weights becomes remarkably simple once we fix the clustering, i.e., the matrix ΩiA = δG(i),A (or, equivalently, the map G : {i} ↦ {A}, i = 1, …, N, A = 1, …, K, where for the notational convenience we use K to denote the number of clusters in the “ultimate” clustering – see above). Just as in NMF, we wish to approximate the matrix Gis via a product of the weights matrix WiA and the exposure matrix HAs, both of which must be nonnegative. More precisely, since we must remove the “overall” mode, i.e., de-noise the matrix Gis, following [8], instead of Gis we will approximate the re-exponentiated demeaned log-counts matrix :
| (10) |
We can include an overall normalization by taking , or , or (recall that is the vector of column means of Xis – see Eq. (5)), etc., to make it look more like the original matrix Gis; however, this does not affect the extracted signatures.33 Also, technically speaking, after re-exponentiating we should “subtract” the extra 1 we added in the definition (3) (assuming we include one of the aforesaid overall normalizations). However, the inherent noise in the data makes this a moot point.
So, we wish to approximate via a product W H. However, with clustering we have , i.e., we have a block (cluster) structure where for a given value of A all WiA are zero except for i ∈ J(A) = {j|G(j) = A}, i.e., for the mutation categories labeled by i that belong to the cluster labeled by A. Therefore, our matrix factorization of Gis into a product W H now simplifies into a set of K independent factorizations as follows:
| (11) |
So, there is no need to run NMF anymore! Indeed, if we can somehow fix HAs for a given cluster, then within this cluster we can determine the corresponding weights (i ∈ J(A)) via a serial linear regression:
| (12) |
where εis are the regression residuals. I.e., for each A ∈ {1, …, K}, we regress the d × nA matrix34 (i ∈ J(A), nA = |J(A)|) over the d-vector HAs (s = 1, …, d), and the regression coefficients are nothing but the nA-vector (i ∈ J(A)), while the residuals are the d × nA matrix . Note that this regression is run without the intercept. Now, this all makes sense as (for each i ∈ J(A)) the regression minimizes the quadratic error term . Furthermore, if HAs are nonnegative, then the weights are automatically nonnegative as they are given by:
| (13) |
Now, we wish these weights to be normalized:
| (14) |
This can always be achieved by rescaling HAs. Alternatively, we can pick HAs without worrying about the normalization, compute via (13), rescale them so that they satisfy (14), and simultaneously accordingly rescale HAs. Mission accomplished!
2.6.1. Fixing exposures
Well, almost… We still need to figure out how to fix the exposures HAs. The simplest way to do this is to note that we can use the matrix ΩiA = δG(i),A to swap the index i in by the index A, i.e., we can take
| (15) |
That is, up to the normalization constants (which are fixed via (14)) we simply take cross-sectional means of in each cluster. (Recall that nA = J(A).) The so-defined HAs are automatically positive as all are positive. Therefore, defined via (13) are also all positive. This is a good news – vanishing would amount to an incomplete weights matrix WiA (i.e., some mutations would belong to no cluster).
So, why does (15) make sense? Looking at (12), we can observe that, if the residuals εis cross-sectionally, within each cluster labeled by A, are random, then we expect that ∑i∈J(A)εis ≈ 0. If we had an exact equality here, then we would have (15) with ηA = 1 (i.e., ) assuming the normalization (14). In practice, the residuals εis are not exactly “random”. First, the number nA of mutation categories in each cluster is not large. Second, as mentioned above, there is variability in serial standard deviations across mutation types. This leads us to consider variations.
2.6.2. A variation
Above we argued that it makes sense to cluster normalized demeaned log-counts due to the cross-sectional variability (and skewness) in the serial standard deviations . We may worry about similar effects in when computing HAs and as we did above. This can be mitigated by using normalized quantities , where are serial variances. That is, we can define35
| (16) |
| (17) |
where νA = ∑i∈J(A)1/ωi. So, 1/ωi are the weights in the averages over the clusters.
2.6.3. Another variation
Here one may wonder, considering the skewed roughly log-normal distribution of Gis and henceforth , would it make sense to relate the exposures to within-cluster cross-sectional averages of demeaned log-counts as opposed to those of ? This is easily achieved. Thus, we can define (this ensures positivity of HAs):
| (18) |
Exponentiating we get
| (19) |
I.e., instead of an arithmetic average as in (15), here we have a geometric average.
As above, here too we can introduce nontrivial weights. Note that the form of (17) is the same as (13), it is only HAs that is affected by the weights. So, we can introduce the weights in the geometric means as follows:
| (20) |
where . Recall that . Thus, we have:
| (21) |
So, the weights are the exponents . Other variations are also possible.
2.7. Implementation
We are now ready to discuss an actual implementation of the above algorithm, much of the R code for which is already provided in [8], [11]. The R source code is given in Appendix A hereof.
3. Empirical results
3.1. Data summary
In our empirical analysis below we use the same genome data (from published samples only) as in [8]. This data is summarized in Table S1 (borrowed from [8]), which gives total counts, number of samples and the data sources, which are as follows: A1 = [36], A2 = [37], B1 = [38], C1 = [39], D1 = [40], E1 = [41], E2 = [42], F1 = [43], G1 = [44], H1 = [45], H2 = [46], I1 = [47], J1 = [48], K1 = [49], L1 = [50], M1 = [51], N1 = [52]. Sample IDs with the corresponding publication sources are given in Appendix A of [8]. In our analysis below we aggregate samples by the 14 cancer types. The resulting data is in Tables S2 and S3. For tables and figures labeled S★ see Supplementary Materials (see Appendix C for a web link).
3.1.1. Structure of data
The underlying data consists of a matrix – call it Gis – whose elements are occurrence counts of mutation types labeled by i = 1, …, N = 96 in samples labeled by s = 1, …, d. More precisely, we can work with one matrix Gis which combines data from different cancer types; or, alternatively, we may choose to work with individual matrices [G(α)]is, where: α = 1, …, n labels n different cancer types; as before, i = 1, …, N = 96; and s = 1, …, d(α). Here d(α) is the number of samples for the cancer type labeled by α. The combined matrix Gis is obtained simply by appending (i.e., bootstrapping) the matrices [G(α)]is together column-wise. In the case of the data we use here (see above), this “big matrix” turns out to have 1389 columns.
Generally, individual matrices [G(α)]is and, thereby, the “big matrix”, contain a lot of noise. For some cancer types we can have a relatively small number of samples. We can also have “sparsely populated” data, i.e., with many zeros for some mutation categories. As mentioned above, different samples are not necessarily uniformly normalized. Etc. The bottom line is that the data is noisy. Furthermore, intuitively it is clear that the larger the matrix we work with, statistically the more “signatures” (or clusters) we should expect to get with any reasonable algorithm. However, as mentioned above, a large number of signatures would be essentially useless and defy the whole purpose of extracting them in the first place – we have 96 mutation categories, so it is clear that the number of signatures cannot be more than 96! If we end up with, say, 50+ signatures, what new or useful does this tell us about the underlying cancers? The answer is likely nothing other than that most cancers have not much in common with each other, which would be a disappointing result from the perspective of therapeutic applications. To mitigate the aforementioned issues, at least to a certain extent, following [8], we can aggregate samples by cancer types. This way we get an N × n matrix, which we also refer to as Gis, where the index s = 1, …, d now takes d = n values corresponding to the cancer types. In the data we use n = 14, the aggregated matrix Gis is much less noisy than the “big matrix”, and we are ready to apply the above machinery to it.
3.2. Genome data results
The 96 × 14 matrix Gis given in Tables S2 and S3 is what we pass into the function bio.cl.sigs() in Appendix A as the input matrix x. We use: iter.max = 100 (this is the maximum number of iterations used in the built-in R function kmeans() – we note that there was not a single instance in our 150 million runs of kmeans() where more iterations were required);36 num.try = 1000 (this is the number of individual k-means samplings we aggregate every time); and num.runs = 150000 (which is the number of aggregated clusterings we use to determine the “ultimate” – that is, the most frequently occurring – clustering). So, we ran k-means 150 million times. More precisely, we ran 15 batches with num.runs = 10000 as a sanity check, to make sure that the final result based on 150,000 aggregated clusterings was consistent with the results based on smaller batches, i.e., that it was in-sample stable.37 Based on Table S4, we identify Clustering-A as the “ultimate” clustering (cf. Clustering-B/C/D).
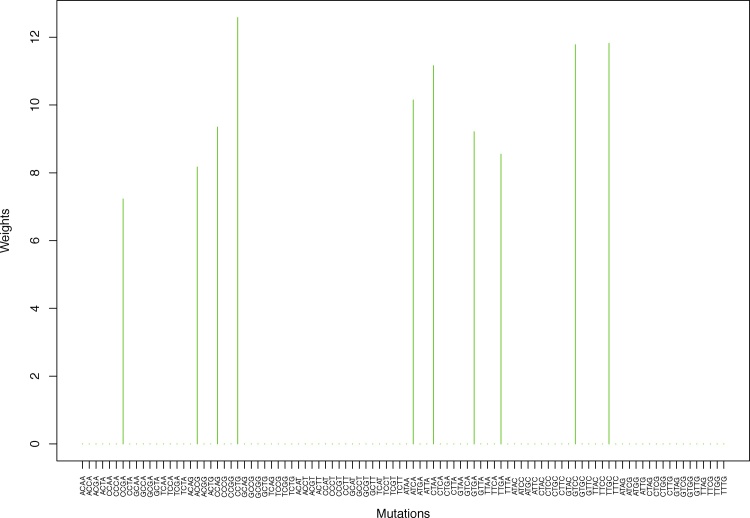
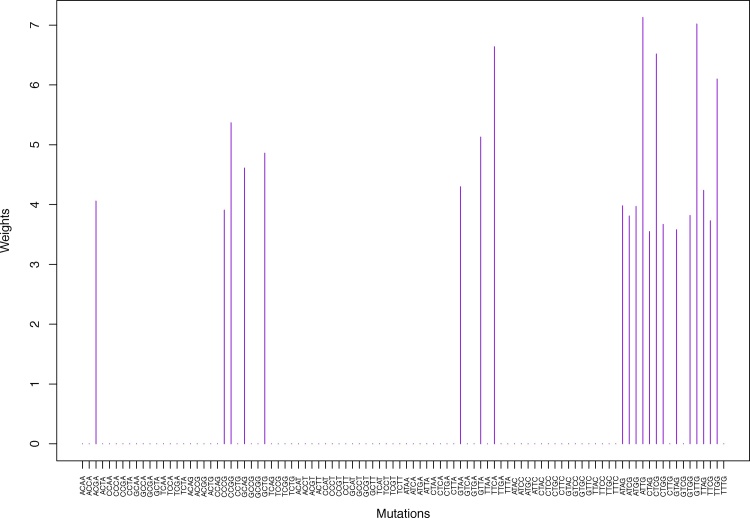
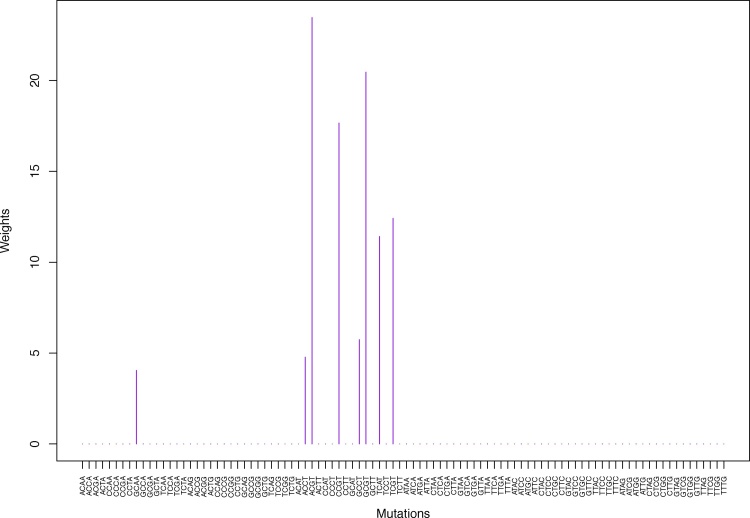
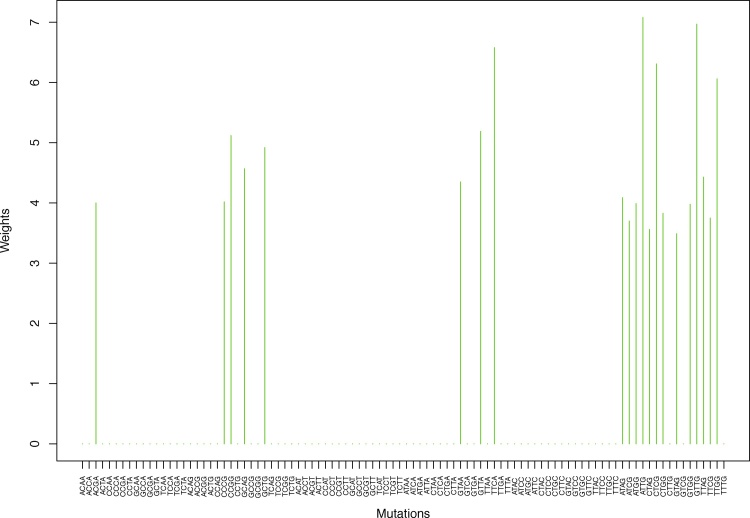
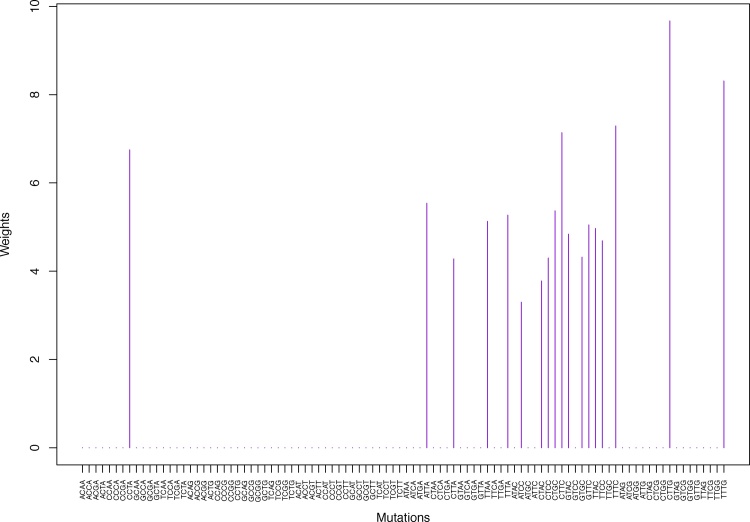
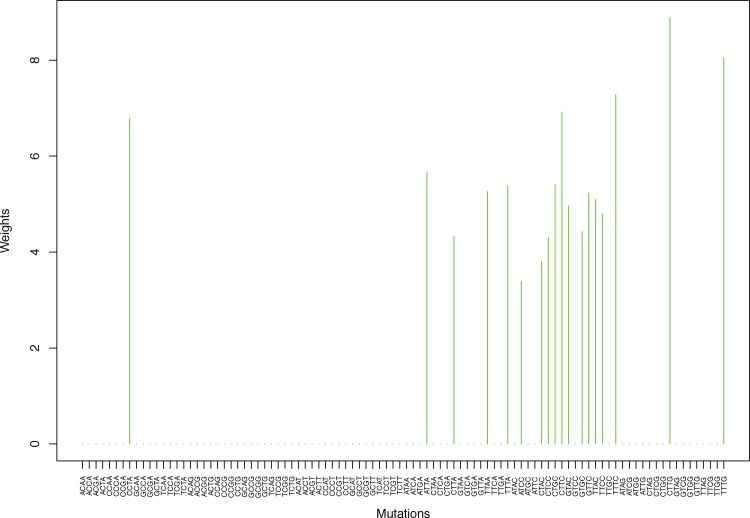
We give the weights for Clustering-A, Clustering-B, Clustering-C and Clustering-D using unnormalized and normalized regressions with exposures computed based on arithmetic averages (see Section 2.6) in Tables 1, 2, S5–S10, and Figs. 2 through Fig. 15 and S1 through S40. We give the weights for Clustering-A using unnormalized and normalized regressions with exposures computed based on geometric averages (see Section 2.6) in Tables 3, 4, and Figs. S41 through S54. The actual mutation categories in each cluster for a given clustering can be read off the aforesaid tables with the weights (the mutation categories with nonzero weights belong to a given cluster), or from the horizontal axis labels in the aforesaid figures. It is evident that Clustering-A, Clustering-B, Clustering-C and Clustering-D are essentially variations of each other (Clustering-D has only 6 clusters, while the other 3 have 7 clusters).
Fig. 4.
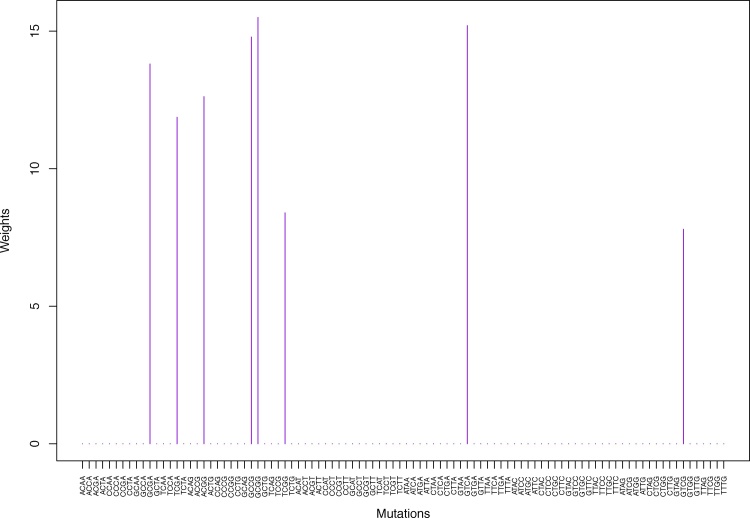
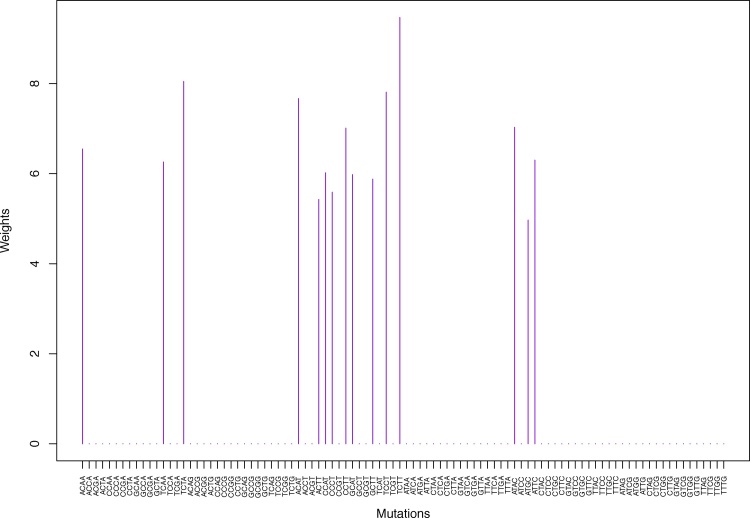
Cluster Cl-2 in Clustering-A with weights based on unnormalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2 .
Fig. 5.
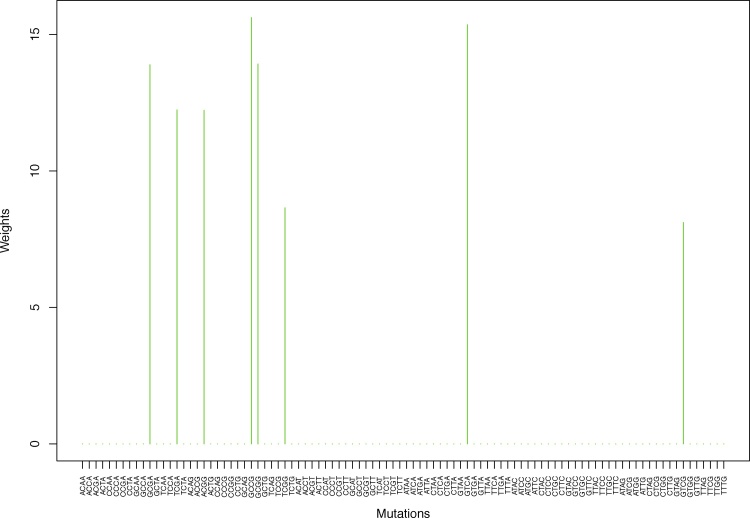
Cluster Cl-2 in Clustering-A with weights based on normalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Fig. 6.
Cluster Cl-3 in Clustering-A with weights based on unnormalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Fig. 7.
Cluster Cl-3 in Clustering-A with weights based on normalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
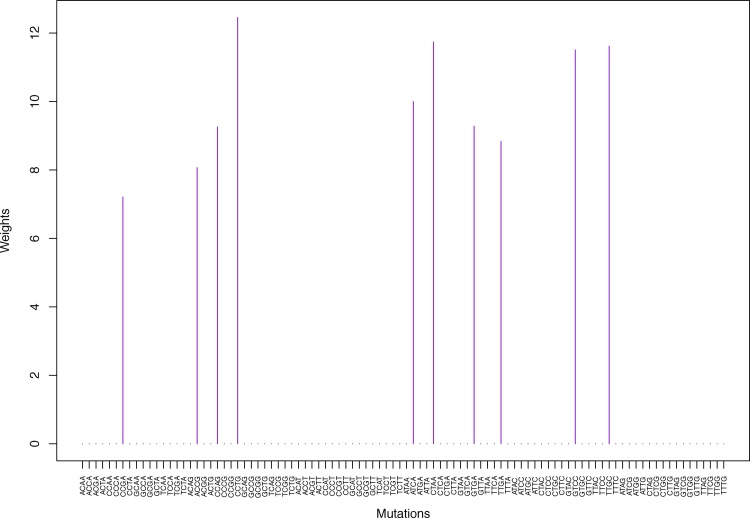
Fig. 14.
Cluster Cl-7 in Clustering-A with weights based on unnormalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Table 2.
Table 1 continued: weights for the next 48 mutation categories.
| Mutation | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ATAA | 0.00 | 0.00 | 0.00 | 0.00 | 4.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.52 | 0.00 | 0.00 |
| ATCA | 0.00 | 0.00 | 10.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 10.15 | 0.00 | 0.00 | 0.00 | 0.00 |
| ATGA | 0.00 | 0.00 | 0.00 | 0.00 | 4.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.30 | 0.00 | 0.00 |
| ATTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.54 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.66 | 0.00 |
| CTAA | 0.00 | 0.00 | 11.74 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 11.16 | 0.00 | 0.00 | 0.00 | 0.00 |
| CTCA | 0.00 | 0.00 | 0.00 | 0.00 | 3.79 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.98 | 0.00 | 0.00 |
| CTGA | 0.00 | 0.00 | 0.00 | 0.00 | 4.88 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.02 | 0.00 | 0.00 |
| CTTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.28 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.33 | 0.00 |
| GTAA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.35 |
| GTCA | 0.00 | 15.20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 15.36 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GTGA | 0.00 | 0.00 | 9.28 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.21 | 0.00 | 0.00 | 0.00 | 0.00 |
| GTTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.19 |
| TTAA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.26 | 0.00 |
| TTCA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.64 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.58 |
| TTGA | 0.00 | 0.00 | 8.84 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.55 | 0.00 | 0.00 | 0.00 | 0.00 |
| TTTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.27 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.38 | 0.00 |
| ATAC | 0.00 | 0.00 | 0.00 | 7.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.06 | 0.00 | 0.00 | 0.00 |
| ATCC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.39 | 0.00 |
| ATGC | 0.00 | 0.00 | 0.00 | 4.97 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.98 | 0.00 | 0.00 | 0.00 |
| ATTC | 0.00 | 0.00 | 0.00 | 6.30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.34 | 0.00 | 0.00 | 0.00 |
| CTAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.78 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.81 | 0.00 |
| CTCC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.31 | 0.00 |
| CTGC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.37 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.41 | 0.00 |
| CTTC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.14 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.92 | 0.00 |
| GTAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.84 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.96 | 0.00 |
| GTCC | 0.00 | 0.00 | 11.51 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 11.78 | 0.00 | 0.00 | 0.00 | 0.00 |
| GTGC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.32 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.43 | 0.00 |
| GTTC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.23 | 0.00 |
| TTAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.97 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.10 | 0.00 |
| TTCC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.69 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.79 | 0.00 |
| TTGC | 0.00 | 0.00 | 11.62 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 11.82 | 0.00 | 0.00 | 0.00 | 0.00 |
| TTTC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.29 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.28 | 0.00 |
| ATAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.98 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.09 |
| ATCG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.81 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.70 |
| ATGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.97 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.99 |
| ATTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.08 |
| CTAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.55 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.56 |
| CTCG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.52 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.31 |
| CTGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.67 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.83 |
| CTTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.67 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.89 | 0.00 |
| GTAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.58 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.49 |
| GTCG | 0.00 | 7.80 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GTGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.82 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.98 |
| GTTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.97 |
| TTAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.24 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.43 |
| TTCG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.73 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.75 |
| TTGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.06 |
| TTTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.31 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.05 | 0.00 |
Table 4.
Table 3 continued: weights for the next 48 mutation categories.
| Mutation | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ATAA | 0.00 | 0.00 | 0.00 | 0.00 | 4.41 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.51 | 0.00 | 0.00 |
| ATCA | 0.00 | 0.00 | 10.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 10.15 | 0.00 | 0.00 | 0.00 | 0.00 |
| ATGA | 0.00 | 0.00 | 0.00 | 0.00 | 4.15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.25 | 0.00 | 0.00 |
| ATTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.59 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.64 | 0.00 |
| CTAA | 0.00 | 0.00 | 11.34 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 11.10 | 0.00 | 0.00 | 0.00 | 0.00 |
| CTCA | 0.00 | 0.00 | 0.00 | 0.00 | 3.87 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.94 | 0.00 | 0.00 |
| CTGA | 0.00 | 0.00 | 0.00 | 0.00 | 5.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.07 | 0.00 | 0.00 |
| CTTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.33 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.31 | 0.00 |
| GTAA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.33 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.36 |
| GTCA | 0.00 | 15.17 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 15.40 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GTGA | 0.00 | 0.00 | 9.30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.24 | 0.00 | 0.00 | 0.00 | 0.00 |
| GTTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.22 |
| TTAA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.21 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.21 | 0.00 |
| TTCA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.73 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.66 |
| TTGA | 0.00 | 0.00 | 8.62 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.51 | 0.00 | 0.00 | 0.00 | 0.00 |
| TTTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.36 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.35 | 0.00 |
| ATAC | 0.00 | 0.00 | 0.00 | 7.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.08 | 0.00 | 0.00 | 0.00 |
| ATCC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.38 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.40 | 0.00 |
| ATGC | 0.00 | 0.00 | 0.00 | 4.99 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.99 | 0.00 | 0.00 | 0.00 |
| ATTC | 0.00 | 0.00 | 0.00 | 6.34 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.36 | 0.00 | 0.00 | 0.00 |
| CTAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.82 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.81 | 0.00 |
| CTCC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.31 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.32 | 0.00 |
| CTGC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.27 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.35 | 0.00 |
| CTTC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.09 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.01 | 0.00 |
| GTAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.82 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.90 | 0.00 |
| GTCC | 0.00 | 0.00 | 11.65 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 11.80 | 0.00 | 0.00 | 0.00 | 0.00 |
| GTGC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.26 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.36 | 0.00 |
| GTTC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.18 | 0.00 |
| TTAC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.09 | 0.00 |
| TTCC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.69 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.76 | 0.00 |
| TTGC | 0.00 | 0.00 | 11.69 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 11.81 | 0.00 | 0.00 | 0.00 | 0.00 |
| TTTC | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.37 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.31 | 0.00 |
| ATAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.94 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.03 |
| ATCG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.83 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.74 |
| ATGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.01 |
| ATTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.98 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.00 |
| CTAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.52 |
| CTCG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.53 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.37 |
| CTGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.63 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.76 |
| CTTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.36 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.13 | 0.00 |
| GTAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.59 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.51 |
| GTCG | 0.00 | 7.84 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GTGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.87 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.97 |
| GTTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.71 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.77 |
| TTAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.17 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.32 |
| TTCG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.74 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.76 |
| TTGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.09 |
| TTTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.12 | 0.00 |
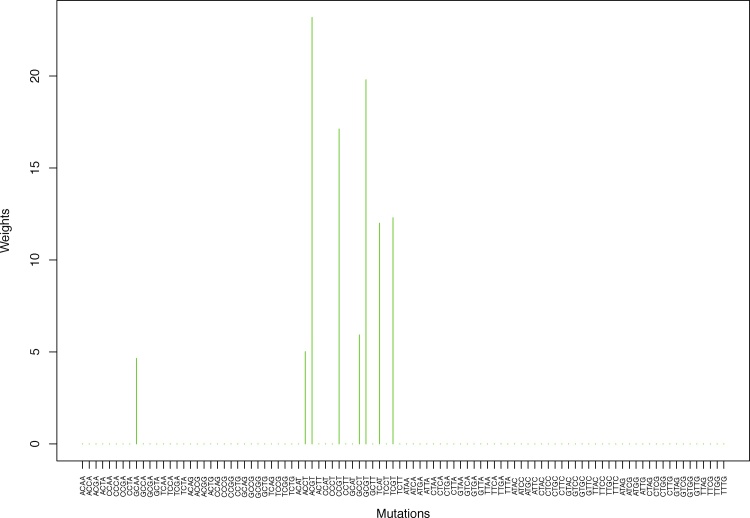
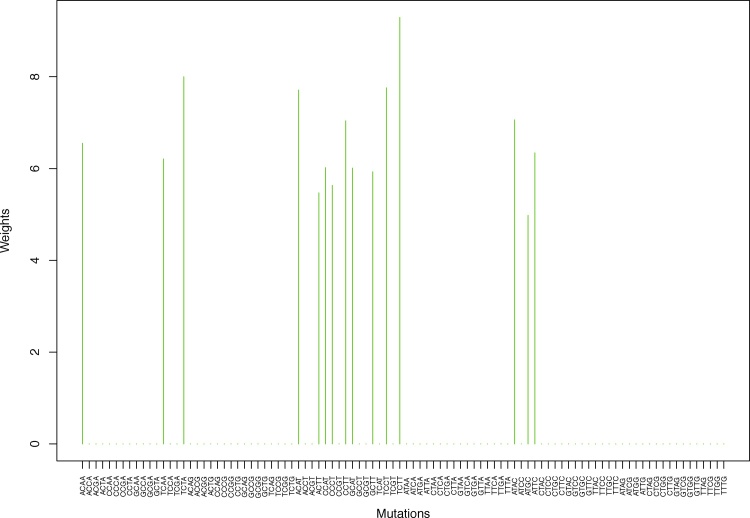
Table 1.
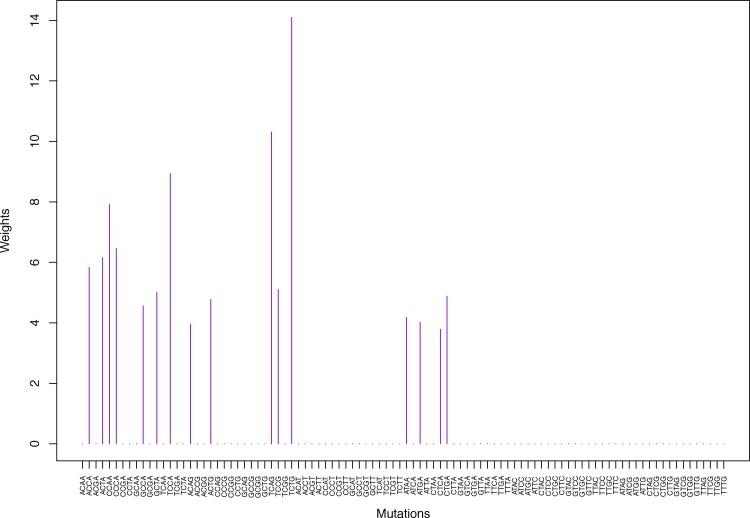
Weights (in the units of 1%, rounded to 2 digits) for the first 48 mutation categories (this table is continued in Table 2 with the next 48 mutation categories) for the 7 clusters in Clustering-A (see Table S4) based on unnormalized (columns 2–8) and normalized (columns 9–15) regressions (see Section 2.6 for details). Each cluster is defined as containing the mutations with nonzero weights. (The mutations are encoded as follows: XYZW = Y>W: XYZ. Thus, GCGA = C>A: GCG.) For instance, cluster Cl-2 contains 8 mutations GCGA, TCGA, ACGG, GCCG, GCGG, TCGG, GTCA, GTCG. In each cluster the weights are normalized to add up to 100% (up to 2 digits due to the aforesaid rounding). In Tables 1 through S10 “weights based on unnormalized regressions” are given by (13), (14) and (15), while “weights based on normalized regressions” are given by (17), (14) and (16), i.e., the exposures are calculated based on arithmetic averages (see Section 2.6 for details).
| Mutation | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACAA | 0.00 | 0.00 | 0.00 | 6.55 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.55 | 0.00 | 0.00 | 0.00 |
| ACCA | 0.00 | 0.00 | 0.00 | 0.00 | 5.83 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.08 | 0.00 | 0.00 |
| ACGA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.06 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.00 |
| ACTA | 0.00 | 0.00 | 0.00 | 0.00 | 6.16 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.38 | 0.00 | 0.00 |
| CCAA | 0.00 | 0.00 | 0.00 | 0.00 | 7.91 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.10 | 0.00 | 0.00 |
| CCCA | 0.00 | 0.00 | 0.00 | 0.00 | 6.46 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.68 | 0.00 | 0.00 |
| CCGA | 0.00 | 0.00 | 7.21 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.23 | 0.00 | 0.00 | 0.00 | 0.00 |
| CCTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.75 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.79 | 0.00 |
| GCAA | 4.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.65 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCCA | 0.00 | 0.00 | 0.00 | 0.00 | 4.56 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.73 | 0.00 | 0.00 |
| GCGA | 0.00 | 13.81 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 13.89 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCTA | 0.00 | 0.00 | 0.00 | 0.00 | 5.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.20 | 0.00 | 0.00 |
| TCAA | 0.00 | 0.00 | 0.00 | 6.26 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.21 | 0.00 | 0.00 | 0.00 |
| TCCA | 0.00 | 0.00 | 0.00 | 0.00 | 8.94 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.29 | 0.00 | 0.00 |
| TCGA | 0.00 | 11.87 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.24 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| TCTA | 0.00 | 0.00 | 0.00 | 8.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.00 | 0.00 | 0.00 | 0.00 |
| ACAG | 0.00 | 0.00 | 0.00 | 0.00 | 3.96 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.18 | 0.00 | 0.00 |
| ACCG | 0.00 | 0.00 | 8.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.17 | 0.00 | 0.00 | 0.00 | 0.00 |
| ACGG | 0.00 | 12.62 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| ACTG | 0.00 | 0.00 | 0.00 | 0.00 | 4.77 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.03 | 0.00 | 0.00 |
| CCAG | 0.00 | 0.00 | 9.26 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.35 | 0.00 | 0.00 | 0.00 | 0.00 |
| CCCG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.91 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.02 |
| CCGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.37 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.12 |
| CCTG | 0.00 | 0.00 | 12.46 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.58 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.61 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.57 |
| GCCG | 0.00 | 14.79 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 15.62 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCGG | 0.00 | 15.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 13.92 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.86 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.92 |
| TCAG | 0.00 | 0.00 | 0.00 | 0.00 | 10.31 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.03 | 0.00 | 0.00 |
| TCCG | 0.00 | 0.00 | 0.00 | 0.00 | 5.10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.95 | 0.00 | 0.00 |
| TCGG | 0.00 | 8.40 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.65 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| TCTG | 0.00 | 0.00 | 0.00 | 0.00 | 14.10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.53 | 0.00 | 0.00 |
| ACAT | 0.00 | 0.00 | 0.00 | 7.67 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.71 | 0.00 | 0.00 | 0.00 |
| ACCT | 4.78 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| ACGT | 23.47 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 23.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| ACTT | 0.00 | 0.00 | 0.00 | 5.43 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.47 | 0.00 | 0.00 | 0.00 |
| CCAT | 0.00 | 0.00 | 0.00 | 6.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.02 | 0.00 | 0.00 | 0.00 |
| CCCT | 0.00 | 0.00 | 0.00 | 5.59 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.63 | 0.00 | 0.00 | 0.00 |
| CCGT | 17.66 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 17.12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| CCTT | 0.00 | 0.00 | 0.00 | 7.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.04 | 0.00 | 0.00 | 0.00 |
| GCAT | 0.00 | 0.00 | 0.00 | 5.98 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.01 | 0.00 | 0.00 | 0.00 |
| GCCT | 5.74 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.93 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCGT | 20.46 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 19.80 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCTT | 0.00 | 0.00 | 0.00 | 5.88 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.93 | 0.00 | 0.00 | 0.00 |
| TCAT | 11.42 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| TCCT | 0.00 | 0.00 | 0.00 | 7.81 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.76 | 0.00 | 0.00 | 0.00 |
| TCGT | 12.42 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| TCTT | 0.00 | 0.00 | 0.00 | 9.47 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.29 | 0.00 | 0.00 | 0.00 |
Fig. 2.
Cluster Cl-1 in Clustering-A with weights based on unnormalized regressions with arithmetic means (see Section 2.6). See Tables S2, 1, and 2. Here and in all figures, for comparison and visualization convenience, we show all 96 channels on the horizontal axis even though the weights are nonzero only for the mutation categories belonging to a given cluster. Thus, in this cluster, only 8 weights are nonzero, to wit, for GCAA, ACCT, ACGT, CCGT, GCCT, GCGT, TCAT, TCGT.
Fig. 15.
Cluster Cl-7 in Clustering-A with weights based on normalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Table 3.
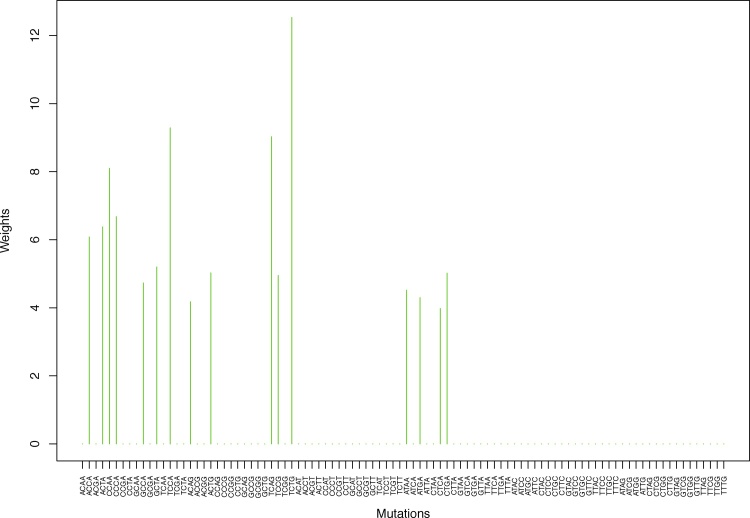
Weights (in the units of 1%, rounded to 2 digits) for the first 48 mutation categories for the 7 clusters in Clustering-A (see Table S4) based on unnormalized (columns 2–8) and normalized (columns 9–15) regressions with the exposures computed via geometric means (see Section 2.6 for details). Here “weights based on unnormalized regressions” are given by (13), (14) and (19), while “weights based on normalized regressions” are given by (17), (14) and (21). Other conventions are the same as in Table 1.
| Mutation | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACAA | 0.00 | 0.00 | 0.00 | 6.54 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.54 | 0.00 | 0.00 | 0.00 |
| ACCA | 0.00 | 0.00 | 0.00 | 0.00 | 6.16 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.20 | 0.00 | 0.00 |
| ACGA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.05 |
| ACTA | 0.00 | 0.00 | 0.00 | 0.00 | 6.38 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.44 | 0.00 | 0.00 |
| CCAA | 0.00 | 0.00 | 0.00 | 0.00 | 8.27 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.27 | 0.00 | 0.00 |
| CCCA | 0.00 | 0.00 | 0.00 | 0.00 | 6.73 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.77 | 0.00 | 0.00 |
| CCGA | 0.00 | 0.00 | 7.32 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.24 | 0.00 | 0.00 | 0.00 | 0.00 |
| CCTA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.77 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.76 | 0.00 |
| GCAA | 4.31 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.68 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCCA | 0.00 | 0.00 | 0.00 | 0.00 | 4.70 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.75 | 0.00 | 0.00 |
| GCGA | 0.00 | 13.79 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 13.76 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCTA | 0.00 | 0.00 | 0.00 | 0.00 | 5.16 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.22 | 0.00 | 0.00 |
| TCAA | 0.00 | 0.00 | 0.00 | 6.22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.20 | 0.00 | 0.00 | 0.00 |
| TCCA | 0.00 | 0.00 | 0.00 | 0.00 | 8.86 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.08 | 0.00 | 0.00 |
| TCGA | 0.00 | 11.96 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.13 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| TCTA | 0.00 | 0.00 | 0.00 | 8.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.01 | 0.00 | 0.00 | 0.00 |
| ACAG | 0.00 | 0.00 | 0.00 | 0.00 | 4.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.16 | 0.00 | 0.00 |
| ACCG | 0.00 | 0.00 | 8.12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.17 | 0.00 | 0.00 | 0.00 | 0.00 |
| ACGG | 0.00 | 12.58 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.32 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| ACTG | 0.00 | 0.00 | 0.00 | 0.00 | 4.73 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.88 | 0.00 | 0.00 |
| CCAG | 0.00 | 0.00 | 9.34 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.36 | 0.00 | 0.00 | 0.00 | 0.00 |
| CCCG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 3.97 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.04 |
| CCGG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.47 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.24 |
| CCTG | 0.00 | 0.00 | 12.56 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.61 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCAG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.68 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.63 |
| GCCG | 0.00 | 14.96 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 15.53 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCGG | 0.00 | 15.17 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 14.18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCTG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.92 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.94 |
| TCAG | 0.00 | 0.00 | 0.00 | 0.00 | 9.40 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.99 | 0.00 | 0.00 |
| TCCG | 0.00 | 0.00 | 0.00 | 0.00 | 4.93 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.90 | 0.00 | 0.00 |
| TCGG | 0.00 | 8.53 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 8.60 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| TCTG | 0.00 | 0.00 | 0.00 | 0.00 | 13.10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.56 | 0.00 | 0.00 |
| ACAT | 0.00 | 0.00 | 0.00 | 7.72 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.73 | 0.00 | 0.00 | 0.00 |
| ACCT | 4.86 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| ACGT | 23.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 23.33 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| ACTT | 0.00 | 0.00 | 0.00 | 5.45 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.47 | 0.00 | 0.00 | 0.00 |
| CCAT | 0.00 | 0.00 | 0.00 | 6.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.02 | 0.00 | 0.00 | 0.00 |
| CCCT | 0.00 | 0.00 | 0.00 | 5.60 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.62 | 0.00 | 0.00 | 0.00 |
| CCGT | 17.45 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 17.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| CCTT | 0.00 | 0.00 | 0.00 | 7.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.05 | 0.00 | 0.00 | 0.00 |
| GCAT | 0.00 | 0.00 | 0.00 | 5.98 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 6.00 | 0.00 | 0.00 | 0.00 |
| GCCT | 5.85 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.97 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCGT | 20.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 19.63 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| GCTT | 0.00 | 0.00 | 0.00 | 5.90 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 5.92 | 0.00 | 0.00 | 0.00 |
| TCAT | 11.55 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| TCCT | 0.00 | 0.00 | 0.00 | 7.77 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 7.75 | 0.00 | 0.00 | 0.00 |
| TCGT | 12.39 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.30 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| TCTT | 0.00 | 0.00 | 0.00 | 9.35 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 9.27 | 0.00 | 0.00 | 0.00 |
3.3. Reconstruction and correlations
So, based on genome data, we have constructed clusterings and weights. Do they work? I.e., do they reconstruct the input data well? It is evident from the get-go that the answer to this question may not be binary in the sense that for some cancer types we might have a nice clustering structure, while for others we may not. The aim of the following exercise is to sort this all out. Here come the correlations…
3.3.1. Within-cluster correlations
We have our de-noised38 matrix . We are approximating this matrix via the following factorized matrix:
| (22) |
We can now compute an n × K matrix ΘsA of within-cluster cross-sectional correlations between and defined via (xCor(·, ·) stands for “cross-sectional correlation” to distinguish it from “serial correlation” Cor(·, ·) we use above)39
| (23) |
We give this matrix for Clustering-A with weights using normalized regressions with exposures computed based on arithmetic means (see Section 2.6) in Table 5. Let us mention that, with exposures based on arithmetic means, weights using normalized regressions work a bit better than using unnormalized regressions. Using exposures based on geometric means changes the weights a bit, which in turn slightly affects the within-cluster correlations, but does not alter the qualitative picture.
Table 5.
The within-cluster cross-sectional correlations ΘsA (columns 2–8), the overall correlations Ξs (column 11) based on the overall cross-sectional regressions, and multiple R2 and adjusted R2 of these regressions (columns 9 and 10). See Section 3.3 for details. Cancer types are labeled by X1 through X14 as in Table S2. All quantities are in the units of 1% rounded to 2 digits. The values above 80% are given in bold font.
| Cancer type | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 | r.sq | adj.r.sq | Overall cor |
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 57.66 | 31.8 | 75.04 | 88.43 | 81.27 | 84.82 | 41.7 | 89.05 | 88.19 | 83.84 |
| X2 | 90.57 | 66.35 | 81.97 | 79.64 | 41.42 | −2.87 | 25.43 | 94.77 | 94.35 | 93.82 |
| X3 | 93.29 | −12.6 | 39.19 | 12.59 | 68.65 | 17.06 | 68.74 | 93.86 | 93.38 | 94.19 |
| X4 | 9.88 | 16.97 | 52.94 | 79.11 | 81.85 | 46.74 | 7.34 | 58.18 | 54.9 | 61.53 |
| X5 | 89.52 | 63.31 | 50.79 | 28.58 | 5.12 | 80.88 | 13.66 | 93.26 | 92.73 | 88.62 |
| X6 | 86.53 | 34.07 | 48.92 | 76.77 | 85.01 | 19.59 | 34.54 | 89.57 | 88.75 | 91.28 |
| X7 | 92.78 | 34.69 | 64.65 | 48.79 | 63.79 | 86.55 | 72.56 | 86.72 | 85.67 | 86.04 |
| X8 | −31.6 | 39.99 | 65.56 | −46.21 | −6.95 | −3.36 | 61.8 | 69.52 | 67.12 | 41.88 |
| X9 | −28.63 | 53.86 | −34.26 | 46.93 | 59.88 | 13.59 | −12.39 | 77.76 | 76.02 | 70.18 |
| X10 | 93.97 | 61.59 | 63.06 | 67.15 | 41.13 | 4.11 | 43.87 | 95.17 | 94.79 | 95.47 |
| X11 | 88.16 | 56.6 | 66.76 | 55.12 | 90.27 | 16.33 | 26.3 | 95.02 | 94.63 | 89.62 |
| X12 | 94.75 | 17.48 | 5.1 | 16.5 | 90 | 27.74 | 21.63 | 94.04 | 93.57 | 96.11 |
| X13 | 97.05 | 58.21 | 75.77 | 78.67 | 88.42 | 20.28 | 44.07 | 96.31 | 96.02 | 95.35 |
| X14 | 38.93 | 65.92 | 17.23 | 58.54 | 4.73 | 35.72 | 31.27 | 82.52 | 81.14 | 65.4 |
3.3.2. Overall correlations
Another useful metric, which we use as a sanity check, is this. For each value of s (i.e., for each cancer type), we can run a linear cross-sectional regression (without the intercept) of over the matrix WiA. So, we have n = 14 of these regressions. Each regression produces multiple R2 and adjusted R2, which we give in Table 5. Furthermore, we can compute the fitted values based on these regressions, which are given by
| (24) |
where (for each value of s) FAs are the regression coefficients. We can now compute the overall cross-sectional correlations (i.e., the index i runs over all N = 96 mutation categories)
| (25) |
These correlations are also given in Table 5 and measure the overall fit quality.
3.3.3. Interpretation
Looking at Table 5 a few things become immediately evident. Clustering works well for 10 out the 14 cancer types we study here. The cancer types for which clustering does not appear to work all that well are Breast Cancer (labeled by X4 in Table 5), Liver Cancer (X8), Lung Cancer (X9), and Renal Cell Carcinoma (X14). More precisely, for Breast Cancer we do have a high within-cluster correlation for Cl-5 (and also Cl-4), but the overall fit is not spectacular due to low within-cluster correlations in other clusters. Also, above 80% within-cluster correlations40 arise for 5 clusters, to wit, Cl-1, Cl-3, Cl-4, Cl-5 and Cl-6, but not for Cl-2 or Cl-7. Furthermore, remarkably, Cl-1 has high within-cluster correlations for 9 cancer types, and Cl-5 for 6 cancer types. These appear to be the leading clusters. Together they have high within-cluster correlations in 11 cancer types. So what does all this mean?
Additional insight is provided by looking at the within-cluster correlations between the 7 cancer signature extracted in [8] and the clusters we find here. Let be the weights for the 7 cancer signatures from Tables 13 and 14 of [8]. We can compute the following within-cluster correlations (α = 1, …, 7 labels the cancer signatures of [8], which we refer to as Sig1 through Sig7):
| (26) |
These correlations are given in Table 6. High within-cluster correlations arise for Cl-1 (with Sig1 and Sig7), Cl-5 (with Sig2) and Cl-6 (with Sig4). And this makes perfect sense. Indeed, looking at Figs. 14 through 20 of [8], Sig1, Sig2, Sig4 and Sig7 are precisely the cancer signatures that have “peaks” (or “spikes” – “tall mountain landscapes”), whereas Sig3, Sig5 and Sig6 do not have such “peaks” (“flat” or “rolling hills landscapes”). No wonder such signatures do not have high within-cluster correlations – they simply do not have cluster-like structures. Looking at Fig. 21 in [8], it becomes evident why clustering does not work well for Liver Cancer (X8) – it has a whopping 96% contribution from Sig5! Similarly, Renal Cell Carcinoma (X14) has a 70% contribution from Sig6. Lung Cancer (X9) is dominated by Sig3, hence no cluster-like structure. Finally, Breast Cancer (X4) is dominated by Sig2, which has a high within-cluster correlation with Cl-5, which is why Breast Cancer has a high within-cluster correlation with Cl-5 (but poor overall correlation in Table 5). So, it all makes sense. The question is, what does all this tell us about cancer signatures?
Table 6.
The within-cluster cross-sectional correlations ΔαA between the weights for 7 cancer signatures Sig1 through Sig7 of [8] and the weights (using normalized regressions with exposures based on arithmetic averages) for 7 clusters in Clustering A (see Section 3.3 for details). All quantities are in the units of 1% rounded to 2 digits. The values above 80% are given in bold font.
| Signature | Cl-1 | Cl-2 | Cl-3 | Cl-4 | Cl-5 | Cl-6 | Cl-7 |
|---|---|---|---|---|---|---|---|
| Sig1 | 92.05 | 10.29 | −6.42 | −8.33 | 51.12 | 29.06 | 20.61 |
| Sig2 | −0.37 | 1.75 | 42.13 | 75.58 | 80.12 | −27.92 | −3.34 |
| Sig3 | −51.53 | 54.4 | −37.16 | 28.19 | 32.98 | 12.37 | −17.7 |
| Sig4 | 31.56 | 11.97 | 54.43 | 56.83 | −1.17 | 84.25 | 60.41 |
| Sig5 | −42.53 | 40.31 | 62.96 | −47.62 | −8.34 | −8.39 | 61.61 |
| Sig6 | 47.79 | 40.62 | 17.8 | 27.45 | −27.96 | 16.87 | 16.97 |
| Sig7 | 80.94 | 19.87 | 55.03 | 33.4 | 13.89 | −29.59 | 13.93 |
Quite a bit! It tells us that cancers such as Liver Cancer, Lung Cancer and Renal Cell Carcinoma have little in common with other cancers (and each other)! At least at the level of mutation categories that dominate the genome structure of such cancers. On the other hand, 9 cancers, to wit, Bone Cancer (X2), Brain Lower Grade Glioma (X3), Chronic Lymphocytic Leukemia (X5), Esophageal Cancer (X6), Gastric Cancer (X7), Medulloblastoma (X10), Ovarian Cancer (X11), Pancreatic Cancer (X12) and Prostate Cancer (X13) apparently all have the Cl-1 cluster structure embedded in them substantially. Similarly, 6 cancers, to wit, B Cell Lymphoma (X1), Breast Cancer (X4), Esophageal Cancer(X6), Ovarian Cancer (X11), Pancreatic Cancer (X12) and Prostate Cancer (X13) apparently all have the Cl-5 cluster structure embedded in them substantially. Furthermore, note the overlap between these two lists, to wit, Esophageal Cancer(X6), Ovarian Cancer (X11), Pancreatic Cancer (X12) and Prostate Cancer (X13). We obtained this result purely statistically, with no biologic input, using our clustering algorithm and other statistical methods such as linear regression to obtain the actual weights. It is too early to know whether this insight will aid any therapeutic applications, but that is the hope – similarities in the underlying genomic structures of different cancer types raise hope that therapeutics for one cancer type could perhaps be applicable to other cancer types. On the other hand, our findings above relating to Liver Cancer, Lung Cancer and Renal Cell Carcinoma (and possibly also Breast Cancer, albeit the latter does appear to have a not-so-insignificant overlap with Cl-5, which differentiates it from the aforesaid 3 cancer types) suggest that these cancer types apparently stand out.
4. Concluding remarks
Clustering ideas and techniques have been applied in cancer research in various incarnations and contexts aplenty – for a partial list of works at least to some extent related to our discussion here, see, e.g., [52], [53], [54], [55], [40], [56], [5], [36], [57], [58], [59], [60], [61], [62], [63], [64], [65], [66], [67], [68], [69], [70], [71], [72], [73], [74], [75], [76], [77], [78] and references therein. As mentioned above, even in NMF clustering is used at some (perhaps not-so-evident) layer. What is new in our approach – and hence new results – is that: (i) following [8], we apply clustering to aggregated by cancer types and de-noised data; ii) we use a tried-and-tested in quantitative finance bag of tricks from [11], which improves clustering; and (iii) last but not least, we apply our *K-means algorithm to cancer genome data. As mentioned above, *K-means, unlike vanilla k-means or its other commonly used variations, is essentially deterministic, and it achieves determinism statistically, not by “guessing” initial centers or as in agglomerative hierarchical clustering, which basically “guesses” the initial (e.g., 2-cluster) clustering. Instead, via aggregating a large number of k-means clusterings and statistical examination of the occurrence counts of such aggregations, *K-means takes a mess of myriad vanilla k-means clusterings and systematically reduces randomness and indeterminism without ad hoc initial “guesswork”.
As mentioned above, consistently with the results of [8] obtained via improved NMF techniques, Liver Cancer, Lung Cancer and Renal Cell Carcinoma do not appear to have clustering (sub)structures. This could be both good and bad news. It is a good news because we learned something interesting about these cancer types – and in two complementary ways. However, it could also be a bad news from the therapeutic standpoint. Since these cancer types appear to have little in common with others, it is likely that they would require specialized therapeutics. On the flipside, we should note that it would make sense to exclude these 3 cancer types when running clustering analysis. However, it would also make sense to include other cancer types by utilizing the International Cancer Genome Consortium data, which we leave for future studies. (For comparative reasons, here we used the same data as in [8], which was limited to data samples published as of the date thereof.) This paper is not intended to be an exhaustive empirical study but a proof of concept and an opening of a new avenue for extracting and studying cancer signatures beyond the tools that NMF provides.
And we do find that 11 out of the 14 cancer types we study here have clustering structures substantially embedded in them and clustering overall works well for at least 10 out of these 11 cancer types.41 Now, looking at Fig. 14 of [8], we see that its “peaks” are located at ACGT, CCGT, GCGT and TCGT. The same “peaks” are present in our cluster Cl-1 (see Figs. 2 and 3). Hence the high within-cluster correlation between Cl-1 and Sig1. On the other hand, Sig1 of [8] is essentially the same as the mutational signature 1 of [40], [36], which is due to spontaneous cytosine deamination. So, this is what our cluster Cl-1 describes. Next, looking at Fig. 15 of [8], we see that its “peaks” are located at TCAG, TCTG, TCAT and TCTT. The first two of these “peaks” TCAG and TCTG are present in our Cl-5 (see Figs. 10 and 11), the third “peak” TCAT is present in our Cl-1 (see Figs. 2 and 3), while the fourth “peak” TCTT is present in our Cl-4 (see Figs. 8 and 9), which is consistent with the high within-cluster correlations between Sig2 and Cl-4 and Cl-5, albeit its within-cluster correlation with Cl-1 is poor. Note that Sig2 of [8] is essentially the same as the mutational signatures 2 + 13 of [40], [36], which are due to APOBEC mediated cytosine deamination. In fact, it was reported as a single signature in [36], however, subsequently, it was split into 2 distinct signatures, which usually appear in the same samples.42 Our clustering results indicate that grouping TCAG and TCTG into one signature makes sense as they belong to the same cluster Cl-5. However, grouping TCAT and TCTT together does not appear to make much sense. Looking at the figures for Clustering-A, Clustering-B, Clustering-C and Clustering-D, we see that the TCAT “peak” invariably appears together with the ACGT, CCGT, GCGT and TCGT “peaks” as in Cl-1 in Clustering-A, Cl-2 in Clustering-B, Cl-1 in Clustering-C, and Cl-1 in Clustering-D, but never with TCTT. So, our clustering approach tells us something new beyond the NMF “intuition”. This may have an important implication for Breast Cancer, which, as mentioned above, is dominated by Sig2. Thus, based on our results in Table 5, we see that Breast Cancer has high within-cluster correlations with Cl-4 and Cl-5, but not with Cl-1. This may imply that clustering simply does not work well for Breast Cancer, which would appear to put it in the same “stand-alone” league as Liver Cancer, Lung Cancer and Renal Cell Carcinoma. In any event, clustering invariably suggests that the TCAT “peak” belongs in Cl-1 with the 4 “peaks” ACGT, CCGT, GCGT and TCGT related to spontaneous cytosine deamination, rather than those related to APOBEC mediated cytosine deamination.
Fig. 3.
Cluster Cl-1 in Clustering-A with weights based on normalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Fig. 10.
Cluster Cl-5 in Clustering-A with weights based on unnormalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Fig. 11.
Cluster Cl-5 in Clustering-A with weights based on normalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Fig. 8.
Cluster Cl-4 in Clustering-A with weights based on unnormalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Fig. 9.
Cluster Cl-4 in Clustering-A with weights based on normalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Now, let us check the remaining two signatures of [8] with “tall mountain landscapes” (see above), to wit, Sig4 and Sig7. Looking at Fig. 17 of [8], we see that its “peaks” are at CTTC, TTTC, CTTG and TTTG. The same peaks appear in our Cl-6 (see Figs. 12 and 13). Hence the high within-cluster correlation between Cl-6 and Sig4. Note that Sig4 is essentially the same as the mutational signature 17 of [40], [36], and its underlying mutational process is unknown. Next, looking at Fig. 20 of [8], we see that its “peaks” for the C > G mutations are essentially the same as in Cl-1. Hence the high within-cluster correlation between Cl-7 and Sig1. So, there are no surprises with Sig1, Sig4 and Sig7. However, based on our clustering results, as we discuss above, with Sig2 we do find – what we feel is a pleasant – surprise, that splitting it into two signatures (see above) might be inadequate and the TCAT “peak” might really belong with the Sig1 “peaks” (spontaneous v. APOBEC mediated cytosine deamination). This is exciting as it might be an indication of the limitations of NMF (or clustering…).43
Fig. 12.
Cluster Cl-6 in Clustering-A with weights based on unnormalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
Fig. 13.
Cluster Cl-6 in Clustering-A with weights based on normalized regressions with arithmetic means (see Section 2.6). See Tables S4, 1, and 2.
In Introduction we promised that we would discuss some potential applications of *K-means in quantitative finance, and so here it is. Let us mention that *K-means is universal, oblivious to the input data and applicable in a variety of fields. In quantitative finance *K-means a priori can be applied everywhere clustering methods are used with the added bonus of (statistical) determinism.44 One evident example is statistical industry classifications discussed in [11], where one uses clustering methods to classify stocks. In fact, *K-means is an extension of the methods discussed in [11]. One thing to keep in mind is that in *K-means one sifts through a large number P of aggregations, which can get computationally costly when clustering 2000+ stocks into 100+ clusters.45 Another potential application is in the context of combining alphas (trading signals) – see, e.g., [79]. Yet another application is when we have a term structure, such as a portfolio of bonds (e.g., U.S. Treasuries or some other bonds) with varying maturities, or futures (e.g., Eurodollar futures) with varying deliveries. These cases resemble the genome data more in the sense that the number N of instruments is relatively small (typically even fewer than the number of mutation categories). Another example with a relatively small number of instruments would be a portfolio of various futures for different FX (foreign exchange) pairs (even with the uniform delivery), e.g., USD/EUR, USD/HKD, EUR/AUD, etc., i.e., FX statistical arbitrage. One approach to optimizing risk in such portfolios is by employing clustering methods and a stable, essentially deterministic algorithm such as *K-means can be useful. Hopefully *K-means will prove a valuable tool in cancer research, quantitative finance as well as various other fields (e.g., image recognition).
Conflict of interest
Authors declare no conflict of interest.
Handled by Jim Huggett
Footnotes
Another practical application is prevention by pairing the signatures extracted from cancer samples with those caused by known carcinogens (e.g., tobacco, aflatoxin, UV radiation, etc).
In brief, DNA is a double helix of two strands, and each strand is a string of letters A, C, G, T corresponding to adenine, cytosine, guanine and thymine, respectively. In the double helix, A in one strand always binds with T in the other, and G always binds with C. This is known as base complementarity. Thus, there are six possible base mutations C>A, C>G, C>T, T>A, T>C, T>G, whereas the other six base mutations are equivalent to these by base complementarity. Each of these 6 possible base mutations is flanked by 4 possible bases on each side thereby producing 4 × 6 ×4 = 96 distinct mutation categories.
Nonlinearities could undermine this argument. However, again, it all boils down to usefulness.
Other issues include: (i) out-of-sample instability, i.e., the signatures obtained from non-overlapping sets of samples can be dramatically different; (ii) in-sample instability, i.e., the signatures can have a strong dependence on the initial iteration choice; and (iii) samples with low counts or sparsely populated samples (i.e., those with many zeros – such samples are ubiquitous, e.g., in exome data) are usually deemed not too useful as they contribute to the in-sample instability.
As a result, now we have the so-aggregated matrix Gis, where s = 1, …, d, and d = n is the number of cancer types, not of samples. This matrix is much less noisy than the sample data.
By “noise” we mean the statistical errors in the weighs obtained by averaging. Typically, such error bars are not reported in the literature on cancer signatures. Usually they are large.
Deterministic (e.g., agglomerative hierarchical) algorithms have their own issues (see below).
As we discuss below, in this regard NMF is not dissimilar.
E.g., splitting the data into 2 initial clusters.
Such as quantitative trading, where out-of-sample performance can be objectively measured. There empirical evidence suggests that such deterministic algorithms underperform so long as nondeterministic ones are used thoughtfully [11].
We should point out that at some level of alignment one may employ a deterministic (e.g., agglomerative hierarchical – see above) clustering algorithm to terminate the malicious circle, which can be a reasonable approach assuming there is enough stability in the data. However, this too adds a(n often hard to quantify and therefore hidden) systematic error to the resultant signatures.
And such error bars are rarely displayed in the prevalent literature…
This would require a highly recursive algorithm.
Which are preferred over deterministic ones for the reasons discussed above.
Below we will discuss what Xis should be for cancer signatures.
Throughout this paper “cross-sectional” refers to “over the index i”.
Note that here the superscript r in , Gr(i) and (see below) is an index, not a power.
This is because things are pretty much random and the only “distribution” at hand is flat.
In finance the analog of this is the so-called “market” mode (see, e.g., [21] and references therein) corresponding to the overall movement of the broad market, which affects all stocks (to varying degrees) – cash inflow (outflow) into (from) the market tends to push stock prices higher (lower). This is the market risk factor, and to mitigate it one can, e.g., hold a dollar-neutral portfolio of stocks (i.e., the same dollar holdings for long and short positions).
Throughout this paper “serial” refers to “over the index s”.
The overall normalization of Cij, i.e., d − 1 (unbiased estimate) vs. d (maximum likelihood estimate) in the denominator in the definition of Cij in (4), is immaterial for our purposes here.
So, in this case d = n = 14 in (4).
For the reasons discussed above, we should demean Xis, not Gis.
More precisely, the discussion of [11] is in the financial context, to wit, quantitative trading, which has its own nuances (see below). However, some of that discussion is quite general and can be adapted to a wide variety of applications.
Qu. = Quartile, SD = Standard Deviation, MAD = Mean Absolute Deviation.
A variety of methods for fixing the number of clusters have been discussed in other contexts, e.g., [22], [23], [24], [25], [26], [27], [28], [29].
In the financial context, these are known as statistical risk models [9]. For a discussion and literature on multifactor risk models, see, e.g., [30], [31] and references therein. For prior works on fixing the number of statistical risk factors, see, e.g., [32], [33].
Here Round(·) can be replaced by floor(·) = ⌊·⌋.
Note that using normalized demeaned log-counts gives the same Ψij.
This is because each column of W, being weights, is normalized to add up to 1.
The superscript T denotes matrix transposition.
I.e., here we assume that εis/ωi are approximately random in (12).
The R function kmeans() produces a warning if it does not converge within iter.max.
We ran these 15 batches consecutively, and each batch produced the same top-10 (by occurrence counts) clusterings as in Table S4; however, the actual occurrence counts are different across the batches with slight variability in the corresponding rankings. The results are pleasantly stable.
De-noising per se does not affect cross-sectional correlations. Adding extra 1 in (3) (recall that we obtain by cross-sectionally demeaning Xis and then re-exponentiating) has a negligible effect. So, in the correlations below we can use the original data matrix Gis instead of .
Due to the factorized structure (22), these correlations do not directly depend on HAs.
The 80% cutoff is somewhat arbitrary, but reasonable.
Breast Cancer possibly being an exception. As mentioned above, it would make sense to exclude Liver Cancer, Lung Cancer and Renal Cell Carcinoma from the analysis, which may affect how well clustering works for Breast Cancer and possibly also the other 10 cancer types.
For detailed comments, see http://cancer.sanger.ac.uk/cosmic/signatures.
Or both… Alternatively – and that would be truly exciting – perhaps there is a biologic explanation. In any event, it is too early to tell – yet another possibility is that this is merely an artifact of the dataset we use. More research and analyses on larger datasets (see above) is needed.
Albeit with the understanding that it requires additional computational cost.
This can be mitigated by employing top-down clustering [11].
The source code in Appendix A hereof is not written to be “fancy” or optimized for speed or in any other way. Its sole purpose is to illustrate the algorithms described in the main text in a simple-to-understand fashion. See Appendix B for some important legalese.
The definition of qrm.calc.norm.ret() in [11] accounts for some peculiarities and nuances pertinent to quantitative trading, which are not applicable here.
The code returns the K clusters ordered such that the number of mutation nA (i.e., the column sum of ΩiA) in the cluster labeled by A is in the increasing order. It also orders clusters with identical nA. We note, however, that (for presentational convenience reasons) the order of such clusters in the tables and figures below is not necessarily the same as what this code returns.
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.bdq.2017.07.001.
Contributor Information
Zura Kakushadze, Email: zura@quantigic.com.
Willie Yu, Email: willie.yu@duke-nus.edu.sg.
Appendix A. R source code
In this appendix we give the R (R Package for Statistical Computing, http://www.r-project.org) source code for computing the clusterings and weights using the algorithms of Section 2. The code is straightforward and self-explanatory.46 The main function is bio.cl.sigs(x, iter.max = 100, num.try = 1000, num.runs = 10000). Here: x is the N × d occurrence counts matrix Gis (where N = 96 is the number of mutation categories, and d is the number of samples; or d = n, where n is the number of cancer types, when the samples are aggregated by cancer types); iter.max is the maximum number of iterations that are passed into the R built-in function kmeans(); num.try is the number M of aggregated clusterings (see Section 2.3.2); num.runs is the number of runs P used to determine the most frequently occurring clustering (the “ultimate” clustering) obtained via aggregation (see Section 2.3.3). The function bio.erank.pc() is defined in Appendix B of [8]. The function qrm.stat.ind.class() is defined in Appendix A of [11]. This function internally calls another function qrm.calc.norm.ret(), which we redefine here via the function bio.calc.norm.ret().47 The output is a list, whose elements are as follows: res$ind is an N × K binary matrix ΩiA = δG(i),A (i = 1, …, N, A = 1, …, K, the map G : {1, …, N} ↦ {1, …, K} – see Section 2), which defines the K clusters in the “ultimate” clustering;48 res$w is an N-vector of weights obtained via unnormalized regressions using arithmetic means for computing exposures (i.e., via (13), (14) and (15)); res$v is an N-vector of weights obtained via normalized regressions using arithmetic means for computing exposures (i.e., via (17), (14) and (16)); res$w.g is an N-vector of weights obtained via unnormalized regressions using geometric means for computing exposures (i.e., via (13), (14) and (19)); res$v.g is an N-vector of weights obtained via normalized regressions using geometric means for computing exposures (i.e., via (17), (14) and (21)).
| bio.calc.norm.ret <- function (ret) |
| { |
| s <- apply(ret, 1, sd) |
| x <- ret / s |
| return(x) |
| } |
| qrm.calc.norm.ret <- bio.calc.norm.ret |
| bio.cl.sigs <- function(x, iter.max = 100, |
| num.try = 1000, num.runs = 10000) |
| { |
| cl.ix <- function(x) match(1, x) |
| y <- log(1 + x) |
| y <- t(t(y) - colMeans(y)) |
| x.d <- exp(y) |
| k <- ncol(bio.erank.pc(y)$pc) |
| n <- nrow(x) |
| u <- rnorm(n, 0, 1) |
| q <- matrix(NA, n, num.runs) |
| p <- rep(NA, num.runs) |
| for(i in 1:num.runs) |
| { |
| z <- qrm.stat.ind.class(y, k, iter.max = iter.max, |
| num.try = num.try, demean.ret = F) |
| p[i] <- sum((residuals(lm(u ∼ -1 + z)))ˆ2) |
| q[, i] <- apply(z, 1, cl.ix) |
| } |
| p1 <- unique(p) |
| ct <- rep(NA, length(p1)) |
| for(i in 1:length(p1)) |
| ct[i] <- sum(p1[i] == p) |
| p1 <- p1[ct == max(ct)] |
| i <- match(p1, p)[1] |
| ix <- q[, i] |
| k <- max(ix) |
| z <- matrix(NA, n, k) |
| for(j in 1:k) |
| z[, j] <- as.numeric(ix == j) |
| res <- bio.cl.wts(x.d, z) |
| return(res) |
| } |
| bio.cl.wts <- function (x, ind) |
| { |
| first.ix <- function(x) match(1, x)[1] |
| calc.wts <- function(x, use.wts = F, use.geom = F) |
| { |
| if(use.geom) |
| { |
| if(use.wts) |
| s <- apply(log(x), 1, sd) |
| else |
| s <- rep(1, nrow(x)) |
| s <- 1 / s / sum(1 / s) |
| fac <- apply(xˆs, 2, prod) |
| } |
| else |
| { |
| if(use.wts) |
| s <- apply(x, 1, sd) |
| else |
| s <- rep(1, nrow(x)) |
| fac <- colMeans(x / s) |
| } |
| w <- coefficients(lm(t(x) ∼ -1 + fac)) |
| w <- 100 * w / sum(w) |
| return(w) |
| } |
| n <- nrow(x) |
| w <- w.g <- v <- v.g <- rep(NA, n) |
| z <- colSums(ind) |
| z <- as.numeric(paste(z, ".", apply(ind, 2, first.ix), sep = "")) |
| dimnames(ind)[[2]] <- names(z) <- 1:ncol(ind) |
| z <- sort(z) |
| z <- names(z) |
| ind <- ind[, z] |
| dimnames(ind)[[2]] <- NULL |
| for(i in 1:ncol(ind)) |
| { |
| take <- ind[, i] == 1 |
| if(sum(take) == 1) |
| { |
| w[take] <- w.g[take] <- 1 |
| v[take] <- v.g[take] <- 1 |
| next |
| } |
| w[take] <- calc.wts(x[take,], F, F) |
| w.g[take] <- calc.wts(x[take,], F, T) |
| v[take] <- calc.wts(x[take,], T, F) |
| v.g[take] <- calc.wts(x[take,], T, T) |
| } |
| res <- new.env() |
| res$ind <- ind |
| res$w <- w |
| res$w.g <- w.g |
| res$v <- v |
| res$v.g <- v.g |
| return(res) |
| } |
Appendix B. Disclaimers
Wherever the context so requires, the masculine gender includes the feminine and/or neuter, and the singular form includes the plural and vice versa. The author of this paper (“Author”) and his affiliates including without limitation Quantigic® Solutions LLC (“Author's Affiliates” or “his Affiliates”) make no implied or express warranties or any other representations whatsoever, including without limitation implied warranties of merchantability and fitness for a particular purpose, in connection with or with regard to the content of this paper including without limitation any code or algorithms contained herein (“Content”).
The reader may use the Content solely at his/her/its own risk and the reader shall have no claims whatsoever against the Author or his Affiliates and the Author and his Affiliates shall have no liability whatsoever to the reader or any third party whatsoever for any loss, expense, opportunity cost, damages or any other adverse effects whatsoever relating to or arising from the use of the Content by the reader including without any limitation whatsoever: any direct, indirect, incidental, special, consequential or any other damages incurred by the reader, however caused and under any theory of liability; any loss of profit (whether incurred directly or indirectly), any loss of goodwill or reputation, any loss of data suffered, cost of procurement of substitute goods or services, or any other tangible or intangible loss; any reliance placed by the reader on the completeness, accuracy or existence of the Content or any other effect of using the Content; and any and all other adversities or negative effects the reader might encounter in using the Content irrespective of whether the Author or his Affiliates is or are or should have been aware of such adversities or negative effects.
The R code included in Appendix A hereof is part of the copyrighted R code of Quantigic® Solutions LLC and is provided herein with the express permission of Quantigic® Solutions LLC. The copyright owner retains all rights, title and interest in and to its copyrighted source code included in Appendix A hereof and any and all copyrights therefore.
Appendix C. Supplementary data
The following are the supplementary data to this article:
References
- 1.Goodman M.F., Fygenson K.D. DNA polymerase fidelity: from genetics toward a biochemical understanding. Genetics. 1998;148(4):1475–1482. doi: 10.1093/genetics/148.4.1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lindahl T. Instability and decay of the primary structure of DNA. Nature. 1993;362(6422):709–715. doi: 10.1038/362709a0. [DOI] [PubMed] [Google Scholar]
- 3.Loeb L.A., Harris C.C. Advances in chemical carcinogenesis: a historical review and perspective. Cancer Res. 2008;68(17):6863–6872. doi: 10.1158/0008-5472.CAN-08-2852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ananthaswamy H.N., Pierceall W.E. Molecular mechanisms of ultraviolet radiation carcinogenesis. Photochem. Photobiol. 1990;52(6):1119–1136. doi: 10.1111/j.1751-1097.1990.tb08452.x. [DOI] [PubMed] [Google Scholar]
- 5.Alexandrov L.B., Nik-Zainal S., Wedge D.C., Campbell P.J., Stratton M.R. Deciphering signatures of mutational processes operative in human cancer. Cell Rep. 2013;3(1):246–259. doi: 10.1016/j.celrep.2012.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Paatero P., Tapper U. Positive matrix factorization: a non-negative factor model with optimal utilization of error. Environmetrics. 1994;5(1):111–126. [Google Scholar]
- 7.Lee D.D., Seung H.S. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401(6755):788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
- 8.Kakushadze Z., Yu W. Factor models for cancer signatures. Physica A. 2016;462:527–559. Available online: http://ssrn.com/abstract=2772458. [Google Scholar]
- 9.Kakushadze Z., Yu W. Statistical risk models. J. Invest. Strat. 2017;6(2):1–40. Available online: http://ssrn.com/abstract=2732453. [Google Scholar]
- 10.Roy O., Vetterli M. The effective rank: a measure of effective dimensionality. European Signal Processing Conference (EUSIPCO); Poznań, Poland, September 3–7; 2007. pp. 606–610. [Google Scholar]
- 11.Kakushadze Z., Yu W. Statistical industry classification. J. Risk Control. 2016;3(1):17–65. Available online: http://ssrn.com/abstract=2802753. [Google Scholar]
- 12.Steinhaus H. Sur la division des corps matériels en parties. Bull. Acad. Polon. Sci. 1957;4(12):801–804. [Google Scholar]
- 13.Lloyd S.P. Bell Telephone Laboratories; Murray Hill, NJ: 1957. Least Square Quantization in PCM. Working Paper. [Google Scholar]
- 14.Forgy E.W. Cluster analysis of multivariate data: efficiency versus interpretability of classifications. Biometrics. 1965;21(3):768–769. [Google Scholar]
- 15.MacQueen J.B. Some methods for classification and analysis of multivariate observations. In: LeCam L., Neyman J., editors. Proceedings of the 5th Berkeley Symposium on Mathematical Statistics Probability. University of California Press; Berkeley, CA: 1967. pp. 281–297. [Google Scholar]
- 16.Hartigan J.A. John Wiley & Sons, Inc.; New York, NY: 1975. Clustering Algorithms. [Google Scholar]
- 17.Hartigan J.A., Wong M.A. Algorithm AS 136: a K-means clustering algorithm. J. R. Stat. Soc. Ser. C Appl. Stat. 1979;28(1):100–108. [Google Scholar]
- 18.Lloyd S.P. Least square quantization in PCM. IEEE Trans. Inform. Theory. 1982;28(2):129–137. [Google Scholar]
- 19.Sibson R. SLINK: an optimally efficient algorithm for the single-link cluster method. Comput. J. Br. Comput. Soc. 1973;16(1):30–34. [Google Scholar]
- 20.Murtagh F., Contreras P. Algorithms for hierarchical clustering: an overview. Wiley Interdiscip. Rev. Data Mining Knowl. Discov. 2011;2(1):86–97. [Google Scholar]
- 21.Bouchaud J.-P., Potters M. Financial applications of random matrix theory: a short review. In: Akemann G., Baik J., Di Francesco P., editors. The Oxford Handbook of Random Matrix Theory. Oxford University Press; Oxford, United Kingdom: 2011. [Google Scholar]
- 22.Rousseeuw P.J. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987;20(1):53–65. [Google Scholar]
- 23.Pelleg D., Moore A.W. X-means: extending K-means with efficient estimation of the number of clusters. In: Langley P., editor. Proceedings of the 17th International Conference on Machine Learning. Morgan Kaufman; San Francisco, CA: 2000. pp. 727–734. [Google Scholar]
- 24.Steinbach M., Karypis G., Kumar V. A comparison of document clustering techniques. KDD Workshop Text Mining. 2000;400(1):525–526. [Google Scholar]
- 25.Goutte C., Hansen L.K., Liptrot M.G., Rostrup E. Feature-space clustering for fMRI meta-analysis. Hum. Brain Mapp. 2001;13(3):165–183. doi: 10.1002/hbm.1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sugar C.A., James G.M. Finding the number of clusters in a data set: an information theoretic approach. J. Am. Stat. Assoc. 2003;98(463):750–763. [Google Scholar]
- 27.Hamerly G., Elkan C. Learning the k in k-means. In: Thrun S., editor. vol. 16. MIT Press; Cambridge, MA: 2004. pp. 281–289. (Advances of the Neural Information Processing Systems). [Google Scholar]
- 28.Lletí R., Ortiz M.C., Sarabia L.A., Sánchez M.S. Selecting variables for k-means cluster analysis by using a genetic algorithm that optimises the silhouettes. Anal. Chim. Acta. 2004;515(1):87–100. [Google Scholar]
- 29.De Amorim R.C., Hennig C. Recovering the number of clusters in data sets with noise features using feature rescaling factors. Inform. Sci. 2015;324:126–145. [Google Scholar]
- 30.Grinold R.C., Kahn R.N. McGraw-Hill; New York, NY: 2000. Active Portfolio Management. [Google Scholar]
- 31.Kakushadze Z., Yu W. Multifactor risk models and heterotic CAPM. J. Invest. Strat. 2016;5(4):1–49. Available online: http://ssrn.com/abstract=2722093. [Google Scholar]
- 32.Connor G., Korajczyk R.A. A test for the number of factors in an approximate factor model. J. Finance. 1993;48(4):1263–1291. [Google Scholar]
- 33.Bai J., Ng S. Determining the number of factors in approximate factor models. Econometrica. 2002;70(1):191–221. [Google Scholar]
- 34.Campbell L.L. Minimum coefficient rate for stationary random processes. Inform. Control. 1960;3(4):360–371. [Google Scholar]
- 35.Yang W., Gibson J.D., He T. Coefficient rate and lossy source coding. IEEE Trans. Inform. Theory. 2005;51(1):381–386. [Google Scholar]
- 36.Alexandrov L.B., Nik-Zainal S., Wedge D.C., Aparicio S.A., Behjati S., Biankin A.V., Bignell G.R., Bolli N., Borg A., Børresen-Dale A.L., Boyault S., Burkhardt B., Butler A.P., Caldas C., Davies H.R., Desmedt C., Eils R., Eyfjörd J.E., Foekens J.A., Greaves M., Hosoda F., Hutter B., Ilicic T., Imbeaud S., Imielinski M., Jäger N., Jones D.T., Jones D., Knappskog S., Kool M., Lakhani S.R., López-Otín C., Martin S., Munshi N.C., Nakamura H., Northcott P.A., Pajic M., Papaemmanuil E., Paradiso A., Pearson J.V., Puente X.S., Raine K., Ramakrishna M., Richardson A.L., Richter J., Rosenstiel P., Schlesner M., Schumacher T.N., Span P.N., Teague J.W., Totoki Y., Tutt A.N., Valdés-Mas R., van Buuren M.M., van ’t Veer L., Vincent-Salomon A., Waddell N., Yates L.R., Australian Pancreatic Cancer Genome Initiative, ICGC Breast Cancer Consortium, ICGC MMML-Seq Consortium, ICGC PedBrain, Zucman-Rossi J., Futreal P.A., McDermott U., Lichter P., Meyerson M., Grimmond S.M., Siebert R., Campo E., Shibata T., Pfister S.M., Campbell P.J., Stratton M.R. Signatures of mutational processes in human cancer. Nature. 2013;500(7463):415–421. doi: 10.1038/nature12477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Love C., Sun Z., Jima D., Li G., Zhang J., Miles R., Richards K.L., Dunphy C.H., Choi W.W., Srivastava G., Lugar P.L., Rizzieri D.A., Lagoo A.S., Bernal-Mizrachi L., Mann K.P., Flowers C.R., Naresh K.N., Evens A.M., Chadburn A., Gordon L.I., Czader M.B., Gill J.I., Hsi E.D., Greenough A., Moffitt A.B., McKinney M., Banerjee A., Grubor V., Levy S., Dunson D.B., Dave S.S. The genetic landscape of mutations in Burkitt lymphoma. Nat. Genet. 2012;44(12):1321–1325. doi: 10.1038/ng.2468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tirode F., Surdez D., Ma X., Parker M., Le Deley M.C., Bahrami A., Zhang Z., Lapouble E., Grossetête-Lalami S., Rusch M., Reynaud S., Rio-Frio T., Hedlund E., Wu G., Chen X., Pierron G., Oberlin O., Zaidi S., Lemmon G., Gupta P., Vadodaria B., Easton J., Gut M., Ding L., Mardis E.R., Wilson R.K., Shurtleff S., Laurence V., Michon J., Marec-Bérard P., Gut I., Downing J., Dyer M., Zhang J., Delattre O., ST. Jude Children's Research Hospital - Washington University Pediatric Cancer Genome Project and the International Cancer Genome Consortium Genomic landscape of Ewing sarcoma defines an aggressive subtype with co-association of STAG2 and TP53 mutations. Cancer Discov. 2014;4(11):1342–1353. doi: 10.1158/2159-8290.CD-14-0622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhang J., Wu G., Miller C.P., Tatevossian R.G., Dalton J.D., Tang B., Orisme W., Punchihewa C., Parker M., Qaddoumi I., Boop F.A., Lu C., Kandoth C., Ding L., Lee R., Huether R., Chen X., Hedlund E., Nagahawatte P., Rusch M., Boggs K., Cheng J., Becksfort J., Ma J., Song G., Li Y., Wei L., Wang J., Shurtleff S., Easton J., Zhao D., Fulton R.S., Fulton L.L., Dooling D.J., Vadodaria B., Mulder H.L., Tang C., Ochoa K., Mullighan C.G., Gajjar A., Kriwacki R., Sheer D., Gilbertson R.J., Mardis E.R., Wilson R.K., Downing J.R., Baker S.J., Ellison D.W., St. Jude Children's Research Hospital-Washington University Pediatric Cancer Genome Project Whole-genome sequencing identifies genetic alterations in pediatric low-grade gliomas. Nat. Genet. 2013;45(6):602–612. doi: 10.1038/ng.2611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nik-Zainal S., Alexandrov L.B., Wedge D.C., Van Loo P., Greenman C.D., Raine K., Jones D., Hinton J., Marshall J., Stebbings L.A., Menzies A., Martin S., Leung K., Chen L., Leroy C., Ramakrishna M., Rance R., Lau K.W., Mudie L.J., Varela I., McBride D.J., Bignell G.R., Cooke S.L., Shlien A., Gamble J., Whitmore I., Maddison M., Tarpey P.S., Davies H.R., Papaemmanuil E., Stephens P.J., McLaren S., Butler A.P., Teague J.W., Jönsson G., Garber J.E., Silver D., Miron P., Fatima A., Boyault S., Langerød A., Tutt A., Martens J.W., Aparicio S.A., Borg Å., Salomon A.V., Thomas G., Børresen-Dale A.L., Richardson A.L., Neuberger M.S., Futreal P.A., Campbell P.J., Stratton M.R., Breast Cancer Working Group of the International Cancer Genome Consortium Mutational processes molding the genomes of 21 breast cancers. Cell. 2012;149(5):979–993. doi: 10.1016/j.cell.2012.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Puente X.S., Pinyol M., Quesada V., Conde L., Ordó nez G.R., Villamor N., Escaramis G., Jares P., Beà S., González-Díaz M., Bassaganyas L., Baumann T., Juan M., López-Guerra M., Colomer D., Tubío J.M., López C., Navarro A., Tornador C., Aymerich M., Rozman M., Hernández J.M., Puente D.A., Freije J.M., Velasco G., Gutiérrez-Fernández A., Costa D., Carrió A., Guijarro S., Enjuanes A., Hernández L., Yagüe J., Nicolás P., Romeo-Casabona C.M., Himmelbauer H., Castillo E., Dohm J.C., de Sanjosé S., Piris M.A., de Alava E., San Miguel J., Royo R., Gelpí J.L., Torrents D., Orozco M., Pisano D.G., Valencia A., Guigó R., Bayés M., Heath S., Gut M., Klatt P., Marshall J., Raine K., Stebbings L.A., Futreal P.A., Stratton M.R., Campbell P.J., Gut I., López-Guillermo A., Estivill X., Montserrat E., López-Otín C., Campo E. Whole-genome sequencing identifies recurrent mutations in chronic lymphocytic leukaemia. Nature. 2011;475(7354):101–105. doi: 10.1038/nature10113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Puente X.S., Beà S., Valdés-Mas R., Villamor N., Gutiérrez-Abril J., Martín-Subero J.I., Munar M., Rubio-Pérez C., Jares P., Aymerich M., Baumann T., Beekman R., Belver L., Carrio A., Castellano G., Clot G., Colado E., Colomer D., Costa D., Delgado J., Enjuanes A., Estivill X., Ferrando A.A., Gelpí J.L., González B., González S., González M., Gut M., Hernández-Rivas J.M., López-Guerra M., Martín-García D., Navarro A., Nicolás P., Orozco M., Payer Á.R., Pinyol M., Pisano D.G., Puente D.A., Queirós A.C., Quesada V., Romeo-Casabona C.M., Royo C., Royo R., Rozman M., Russi nol N., Salaverría I., Stamatopoulos K., Stunnenberg H.G., Tamborero D., Terol M.J., Valencia A., López-Bigas N., Torrents D., Gut I., López-Guillermo A., López-Otín C., Campo E. Non-coding recurrent mutations in chronic lymphocytic leukaemia. Nature. 2015;526(7574):519–524. doi: 10.1038/nature14666. [DOI] [PubMed] [Google Scholar]
- 43.Cheng C., Zhou Y., Li H., Xiong T., Li S., Bi Y., Kong P., Wang F., Cui H., Li Y., Fang X., Yan T., Li Y., Wang J., Yang B., Zhang L., Jia Z., Song B., Hu X., Yang J., Qiu H., Zhang G., Liu J., Xu E., Shi R., Zhang Y., Liu H., He C., Zhao Z., Qian Y., Rong R., Han Z., Zhang Y., Luo W., Wang J., Peng S., Yang X., Li X., Li L., Fang H., Liu X., Ma L., Chen Y., Guo S., Chen X., Xi Y., Li G., Liang J., Yang X., Guo J., Jia J., Li Q., Cheng X., Zhan Q., Cui Y. Whole-genome sequencing reveals diverse models of structural variations in esophageal squamous cell carcinoma. Am. J. Hum. Genet. 2016;98(2):256–274. doi: 10.1016/j.ajhg.2015.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wang K., Yuen S.T., Xu J., Lee S.P., Yan H.H., Shi S.T., Siu H.C., Deng S., Chu K.M., Law S., Chan K.H., Chan A.S., Tsui W.Y., Ho S.L., Chan A.K., Man J.L., Foglizzo V., Ng M.K., Chan A.S., Ching Y.P., Cheng G.H., Xie T., Fernandez J., Li V.S., Clevers H., Rejto P.A., Mao M., Leung S.Y. Whole-genome sequencing and comprehensive molecular profiling identify new driver mutations in gastric cancer. Nat. Genet. 2014;46(6):573–582. doi: 10.1038/ng.2983. [DOI] [PubMed] [Google Scholar]
- 45.Sung W.K., Zheng H., Li S., Chen R., Liu X., Li Y., Lee N.P., Lee W.H., Ariyaratne P.N., Tennakoon C., Mulawadi F.H., Wong K.F., Liu A.M., Poon R.T., Fan S.T., Chan K.L., Gong Z., Hu Y., Lin Z., Wang G., Zhang Q., Barber T.D., Chou W.C., Aggarwal A., Hao K., Zhou W., Zhang C., Hardwick J., Buser C., Xu J., Kan Z., Dai H., Mao M., Reinhard C., Wang J., Luk J.M. Genome-wide survey of recurrent HBV integration in hepatocellular carcinoma. Nat. Genet. 2012;44(7):765–769. doi: 10.1038/ng.2295. [DOI] [PubMed] [Google Scholar]
- 46.Fujimoto A., Furuta M., Totoki Y., Tsunoda T., Kato M., Shiraishi Y., Tanaka H., Taniguchi H., Kawakami Y., Ueno M., Gotoh K., Ariizumi S., Wardell C.P., Hayami S., Nakamura T., Aikata H., Arihiro K., Boroevich K.A., Abe T., Nakano K., Maejima K., Sasaki-Oku A., Ohsawa A., Shibuya T., Nakamura H., Hama H., Hosoda F., Arai Y., Ohashi S., Urushidate T., Nagae G., Yamamoto S., Ueda H., Tatsuno K., Ojima H., Hiraoka N., Okusaka T., Kubo M., Marubashi S., Yamada T., Hirano S., Yamamoto M., Ohdan H., Shimada K., Ishikawa O., Yamaue H., Chayama K., Miyano S., Aburatani H., Shibata T., Nakagawa H. Whole-genome mutational landscape and characterization of noncoding and structural mutations in liver cancer. Nat. Genet. 2016;48(5):500–509. doi: 10.1038/ng.3547. [DOI] [PubMed] [Google Scholar]
- 47.Imielinski M., Berger A.H., Hammerman P.S., Hernandez B., Pugh T.J., Hodis E., Cho J., Suh J., Capelletti M., Sivachenko A., Sougnez C., Auclair D., Lawrence M.S., Stojanov P., Cibulskis K., Choi K., de Waal L., Sharifnia T., Brooks A., Greulich H., Banerji S., Zander T., Seidel D., Leenders F., Ansén S., Ludwig C., Engel-Riedel W., Stoelben E., Wolf J., Goparju C., Thompson K., Winckler W., Kwiatkowski D., Johnson B.E., Jänne P.A., Miller V.A., Pao W., Travis W.D., Pass H.I., Gabriel S.B., Lander E.S., Thomas R.K., Garraway L.A., Getz G., Meyerson M. Mapping the hallmarks of lung adenocarcinoma with massively parallel sequencing. Cell. 2012;150(6):1107–1120. doi: 10.1016/j.cell.2012.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jones D.T., Jäger N., Kool M., Zichner T., Hutter B., Sultan M., Cho Y.J., Pugh T.J., Hovestadt V., Stütz A.M., Rausch T., Warnatz H.J., Ryzhova M., Bender S., Sturm D., Pleier S., Cin H., Pfaff E., Sieber L., Wittmann A., Remke M., Witt H., Hutter S., Tzaridis T., Weischenfeldt J., Raeder B., Avci M., Amstislavskiy V., Zapatka M., Weber U.D., Wang Q., Lasitschka B., Bartholomae C.C., Schmidt M., von Kalle C., Ast V., Lawerenz C., Eils J., Kabbe R., Benes V., van Sluis P., Koster J., Volckmann R., Shih D., Betts M.J., Russell R.B., Coco S., Tonini G.P., Schüller U., Hans V., Graf N., Kim Y.J., Monoranu C., Roggendorf W., Unterberg A., Herold-Mende C., Milde T., Kulozik A.E., von Deimling A., Witt O., Maass E., Rössler J., Ebinger M., Schuhmann M.U., Frühwald M.C., Hasselblatt M., Jabado N., Rutkowski S., von Bueren A.O., Williamson D., Clifford S.C., McCabe M.G., Collins V.P., Wolf S., Wiemann S., Lehrach H., Brors B., Scheurlen W., Felsberg J., Reifenberger G., Northcott P.A., Taylor M.D., Meyerson M., Pomeroy S.L., Yaspo M.L., Korbel J.O., Korshunov A., Eils R., Pfister S.M., Lichter P. Dissecting the genomic complexity underlying medulloblastoma. Nature. 2012;488(7409):100–105. doi: 10.1038/nature11284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Patch A.M., Christie E.L., Etemadmoghadam D., Garsed D.W., George J., Fereday S., Nones K., Cowin P., Alsop K., Bailey P.J., Kassahn K.S., Newell F., Quinn M.C., Kazakoff S., Quek K., Wilhelm-Benartzi C., Curry E., Leong H.S., Australian Ovarian Cancer Study Group, Hamilton A., Mileshkin L., Au-Yeung G., Kennedy C., Hung J., Chiew Y.E., Harnett P., Friedlander M., Quinn M., Pyman J., Cordner S., O’Brien P., Leditschke J., Young G., Strachan K., Waring P., Azar W., Mitchell C., Traficante N., Hendley J., Thorne H., Shackleton M., Miller D.K., Arnau G.M., Tothill R.W., Holloway T.P., Semple T., Harliwong I., Nourse C., Nourbakhsh E., Manning S., Idrisoglu S., Bruxner T.J., Christ A.N., Poudel B., Holmes O., Anderson M., Leonard C., Lonie A., Hall N., Wood S., Taylor D.F., Xu Q., Fink J.L., Waddell N., Drapkin R., Stronach E., Gabra H., Brown R., Jewell A., Nagaraj S.H., Markham E., Wilson P.J., Ellul J., McNally O., Doyle M.A., Vedururu R., Stewart C., Lengyel E., Pearson J.V., Waddell N., deFazio A., Grimmond S.M., Bowtell D.D. Whole-genome characterization of chemoresistant ovarian cancer. Nature. 2015;521(7553):489–494. doi: 10.1038/nature14410. [DOI] [PubMed] [Google Scholar]
- 50.Waddell N., Pajic M., Patch A.M., Chang D.K., Kassahn K.S., Bailey P., Johns A.L., Miller D., Nones K., Quek K., Quinn M.C., Robertson A.J., Fadlullah M.Z., Bruxner T.J., Christ A.N., Harliwong I., Idrisoglu S., Manning S., Nourse C., Nourbakhsh E., Wani S., Wilson P.J., Markham E., Cloonan N., Anderson M.J., Fink J.L., Holmes O., Kazakoff S.H., Leonard C., Newell F., Poudel B., Song S., Taylor D., Waddell N., Wood S., Xu Q., Wu J., Pinese M., Cowley M.J., Lee H.C., Jones M.D., Nagrial A.M., Humphris J., Chantrill L.A., Chin V., Steinmann A.M., Mawson A., Humphrey E.S., Colvin E.K., Chou A., Scarlett C.J., Pinho A.V., Giry-Laterriere M., Rooman I., Samra J.S., Kench J.G., Pettitt J.A., Merrett N.D., Toon C., Epari K., Nguyen N.Q., Barbour A., Zeps N., Jamieson N.B., Graham J.S., Niclou S.P., Bjerkvig R., Grützmann R., Aust D., Hruban R.H., Maitra A., Iacobuzio-Donahue C.A., Wolfgang C.L., Morgan R.A., Lawlor R.T., Corbo V., Bassi C., Falconi M., Zamboni G., Tortora G., Tempero M.A., Australian Pancreatic Cancer Genome Initiative, Gill A.J., Eshleman J.R., Pilarsky C., Scarpa A., Musgrove E.A., Pearson J.V., Biankin A.V., Grimmond S.M. Whole genomes redefine the mutational landscape of pancreatic cancer. Nature. 2015;518(7540):495–501. doi: 10.1038/nature14169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Gundem G., Van Loo P., Kremeyer B., Alexandrov L.B., Tubio J.M., Papaemmanuil E., Brewer D.S., Kallio H.M., Högnäs G., Annala M., Kivinummi K., Goody V., Latimer C., O’Meara S., Dawson K.J., Isaacs W., Emmert-Buck M.R., Nykter M., Foster C., Kote-Jarai Z., Easton D., Whitaker H.C., ICGC Prostate UK Group, Neal D.E., Cooper C.S., Eeles R.A., Visakorpi T., Campbell P.J., McDermott U., Wedge D.C., Bova G.S. The evolutionary history of lethal metastatic prostate cancer. Nature. 2015;520(7547):353–357. doi: 10.1038/nature14347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Scelo G., Riazalhosseini Y., Greger L., Letourneau L., Gonzàlez-Porta M., Wozniak M.B., Bourgey M., Harnden P., Egevad L., Jackson S.M., Karimzadeh M., Arseneault M., Lepage P., How-Kit A., Daunay A., Renault V., Blanché H., Tubacher E., Sehmoun J., Viksna J., Celms E., Opmanis M., Zarins A., Vasudev N.S., Seywright M., Abedi-Ardekani B., Carreira C., Selby P.J., Cartledge J.J., Byrnes G., Zavadil J., Su J., Holcatova I., Brisuda A., Zaridze D., Moukeria A., Foretova L., Navratilova M., Mates D., Jinga V., Artemov A., Nedoluzhko A., Mazur A., Rastorguev S., Boulygina E., Heath S., Gut M., Bihoreau M.T., Lechner D., Foglio M., Gut I.G., Skryabin K., Prokhortchouk E., Cambon-Thomsen A., Rung J., Bourque G., Brennan P., Tost J., Banks R.E., Brazma A., Lathrop G.M. Variation in genomic landscape of clear cell renal cell carcinoma across Europe. Nat. Commun. 2014;5:5135. doi: 10.1038/ncomms6135. [DOI] [PubMed] [Google Scholar]
- 53.Chen Z., Feng J., Buzin C.H., Sommer S.S. Epidemiology of doublet/multiplet mutations in lung cancers: evidence that a subset arises by chronocoordinate events. PloS ONE. 2008;3(11):e3714. doi: 10.1371/journal.pone.0003714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chen Z., Feng J., Saldivar J.S., Gu D., Bockholt A., Sommer S.S. EGFR somatic doublets in lung cancer are frequent and generally arise from a pair of driver mutations uncommonly seen as singlet mutations: one-third of doublets occur at five pairs of amino acids. Oncogene. 2008;27(31):4336–4343. doi: 10.1038/onc.2008.71. [DOI] [PubMed] [Google Scholar]
- 55.Kashuba V.I., Pavlova T.V., Grigorieva E.V., Kutsenko A., Yenamandra S.P., Li J., Wang F., Protopopov A.I., Zabarovska V.I., Senchenko V., Haraldson K., Eshchenko T., Kobliakova J., Vorontsova O., Kuzmin I., Braga E., Blinov V.M., Kisselev L.L., Zeng Y.-X., Ernberg I., Lerman M.I., Klein G., Zabarovsky E.R. High mutability of the tumor suppressor genes RASSF1 and RBSP3 (CTDSPL) in cancer. PLoS ONE. 2009;4(5):e5231. doi: 10.1371/journal.pone.0005231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Roberts S.A., Sterling J., Thompson C., Harris S., Mav D., Shah R., Klimczak L.J., Kryukov G.V., Malc E., Mieczkowski P.A., Resnick M.A., Gordenin D.A. Clustered mutations in yeast and in human cancers can arise from damaged long single-strand DNA regions. Mol. Cell. 2012;46(4):424–435. doi: 10.1016/j.molcel.2012.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Burns M.B., Lackey L., Carpenter M.A., Rathore A., Land A.M., Leonard B., Refsland E.W., Kotandeniya D., Tretyakova N., Nikas J.B., Yee D., Temiz N.A., Donohue D.E., McDougle R.M., Brown W.L., Law E.K., Harris R.S. APOBEC3B is an enzymatic source of mutation in breast cancer. Nature. 2013;494(7437):366–370. doi: 10.1038/nature11881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Burns M.B., Temiz N.A., Harris R.S. Evidence for APOBEC3B mutagenesis in multiple human cancers. Nat. Genet. 2013;45(9):977–983. doi: 10.1038/ng.2701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lawrence M.S., Stojanov P., Polak P., Kryukov G.V., Cibulskis K., Sivachenko A., Carter S.L., Stewart C., Mermel C.H., Roberts S.A., Kiezun A., Hammerman P.S., McKenna A., Drier Y., Zou L., Ramos A.H., Pugh T.J., Stransky N., Helman E., Kim J., Sougnez C., Ambrogio L., Nickerson E., Shefler E., Cortés M.L., Auclair D., Saksena G., Voet D., Noble M., DiCara D., Lin P., Lichtenstein L., Heiman D.I., Fennell T., Imielinski M., Hernandez B., Hodis E., Baca S., Dulak A.M., Lohr J., Landau D.A., Wu C.J., Melendez-Zajgla J., Hidalgo-Miranda A., Koren A., McCarroll S.A., Mora J., Lee R.S., Crompton B., Onofrio R., Parkin M., Winckler W., Ardlie K., Gabriel S.B., Roberts C.W., Biegel J.A., Stegmaier K., Bass A.J., Garraway L.A., Meyerson M., Golub T.R., Gordenin D.A., Sunyaev S., Lander E.S., Getz G. Mutational heterogeneity in cancer and the search for new cancer-associated genes. Nature. 2013;499(7457):208–214. doi: 10.1038/nature12213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Long J., Delahanty R.J., Li G., Gao Y.T., Lu W., Cai Q., Xiang Y.B., Li C., Ji B.T., Zheng Y., Ali S., Shu X.O., Zheng W. A common deletion in the APOBEC3 genes and breast cancer risk. J. Natl. Cancer Inst. 2013;105(8):573–579. doi: 10.1093/jnci/djt018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Roberts S.A., Lawrence M.S., Klimczak L.J., Grimm S.A., Fargo D., Stojanov P., Kiezun A., Kryukov G.V., Carter S.L., Saksena G., Harris S., Shah R.R., Resnick M.A., Getz G., Gordenin D.A. An APOBEC cytidine deaminase mutagenesis pattern is widespread in human cancers. Nat. Genet. 2013;45(9):970–976. doi: 10.1038/ng.2702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Taylor B.J.M., Nik-Zainal S., Wu Y.L., Stebbings L.A., Raine K., Campbell P.J., Rada C., Stratton M.R., Neuberger M.S. DNA deaminases induce break-associated mutation showers with implication of APOBEC3B and 3A in breast cancer kataegis. eLife. 2013;2:e00534. doi: 10.7554/eLife.00534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Xuan D., Li G., Cai Q., Deming-Halverson S., Shrubsole M.J., Shu X.O., Kelley M.C., Zheng W., Long J. APOBEC3 deletion polymorphism is associated with breast cancer risk among women of European ancestry. Carcinogenesis. 2013;34(10):2240–2243. doi: 10.1093/carcin/bgt185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Alexandrov L.B., Stratton M.R. Mutational signatures: the patterns of somatic mutations hidden in cancer genomes. Curr. Opin. Genet. Dev. 2014;24:52–60. doi: 10.1016/j.gde.2013.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bacolla A., Cooper D.N., Vasquez K.M. Mechanisms of base substitution mutagenesis in cancer genomes. Genes. 2014;5(1):108–146. doi: 10.3390/genes5010108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Bolli N., Avet-Loiseau H., Wedge D.C., Van Loo P., Alexandrov L.B., Martincorena I., Dawson K.J., Iorio F., Nik-Zainal S., Bignell G.R., Hinton J.W., Li Y., Tubio J.M., McLaren S., O’ Meara S., Butler A.P., Teague J.W., Mudie L., Anderson E., Rashid N., Tai Y.T., Shammas M.A., Sperling A.S., Fulciniti M., Richardson P.G., Parmigiani G., Magrangeas F., Minvielle S., Moreau P., Attal M., Facon T., Futreal P.A., Anderson K.C., Campbell P.J., Munshi N.C. Heterogeneity of genomic evolution and mutational profiles in multiple myeloma. Nat. Commun. 2014;5:2997. doi: 10.1038/ncomms3997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Caval V., Suspène R., Shapira M., Vartanian J.P., Wain-Hobson S. A prevalent cancer susceptibility APOBEC3A hybrid allele bearing APOBEC3B 3’UTR enhances chromosomal DNA damage. Nat. Commun. 2014;5:5129. doi: 10.1038/ncomms6129. [DOI] [PubMed] [Google Scholar]
- 68.Davis C.F., Ricketts C.J., Wang M., Yang L., Cherniack A.D., Shen H., Buhay C., Kang H., Kim S.C., Fahey C.C., Hacker K.E., Bhanot G., Gordenin D.A., Chu A., Gunaratne P.H., Biehl M., Seth S., Kaipparettu B.A., Bristow C.A., Donehower L.A., Wallen E.M., Smith A.B., Tickoo S.K., Tamboli P., Reuter V., Schmidt L.S., Hsieh J.J., Choueiri T.K., Hakimi A.A., Cancer Genome Atlas Research Network, Chin L., Meyerson M., Kucherlapati R., Park W.Y., Robertson A.G., Laird P.W., Henske E.P., Kwiatkowski D.J., Park P.J., Morgan M., Shuch B., Muzny D., Wheeler D.A., Linehan W.M., Gibbs R.A., Rathmell W.K., Creighton C.J. The somatic genomic landscape of chromophobe renal cell carcinoma. Cancer Cell. 2014;26(3):319–330. doi: 10.1016/j.ccr.2014.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Helleday T., Eshtad S., Nik-Zainal S. Mechanisms underlying mutational signatures in human cancers. Nat. Rev. Genet. 2014;15(9):585–598. doi: 10.1038/nrg3729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Nik-Zainal S., Wedge D.C., Alexandrov L.B., Petljak M., Butler A.P., Bolli N., Davies H.R., Knappskog S., Martin S., Papaemmanuil E., Ramakrishna M., Shlien A., Simonic I., Xue Y., Tyler-Smith C., Campbell P.J., Stratton M.R. Association of a germline copy number polymorphism of APOBEC3A and APOBEC3B with burden of putative APOBEC-dependent mutations in breast cancer. Nat. Genet. 2014;46(5):487–491. doi: 10.1038/ng.2955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Poon S., McPherson J., Tan P., Teh B., Rozen S. Mutation signatures of carcinogen exposure: genome-wide detection and new opportunities for cancer prevention. Genome Med. 2014;6(3):24. doi: 10.1186/gm541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Qian J., Wang Q., Dose M., Pruett N., Kieffer-Kwon K.R., Resch W., Liang G., Tang Z., Mathé E., Benner C., Dubois W., Nelson S., Vian L., Oliveira T.Y., Jankovic M., Hakim O., Gazumyan A., Pavri R., Awasthi P., Song B., Liu G., Chen L., Zhu S., Feigenbaum L., Staudt L., Murre C., Ruan Y., Robbiani D.F., Pan-Hammarström Q., Nussenzweig M.C., Casellas R. B cell super-enhancers and regulatory clusters recruit AID tumorigenic activity. Cell. 2014;159(7):1524–1537. doi: 10.1016/j.cell.2014.11.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Roberts S.A., Gordenin D.A. eLS (Genetics & Disease) John Wiley & Sons, Ltd.; Chichester, UK: 2014. Clustered mutations in human cancer. [Google Scholar]
- 74.Roberts S.A., Gordenin D.A. Clustered and genome-wide transient mutagenesis in human cancers: hypermutation without permanent mutators or loss of fitness. BioEsseys. 2014;36(4):382–393. doi: 10.1002/bies.201300140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Roberts S.A., Gordenin D.A. Hypermutation in human cancer genomes: footprints and mechanisms. Nat. Rev. Cancer. 2014;14(12):786–800. doi: 10.1038/nrc3816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Sima J., Gilbert D.M. Complex correlations: replication timing and mutational landscapes during cancer and genome evolution. Curr. Opin. Genet. Dev. 2014;25:93–100. doi: 10.1016/j.gde.2013.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Chan K., Gordenin D.A. Clusters of multiple mutations: incidence and molecular mechanisms. Annu. Rev. Genet. 2015;49:243–627. doi: 10.1146/annurev-genet-112414-054714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Pettersen H.S., Galashevskaya A., Doseth B., Sousa M.M., Sarno A., Visnes T., Aas P.A., Liabakk N.B., Slupphaug G., Sætrom P., Kavli B., Krokan H.E. AID expression in B-cell lymphomas causes accumulation of genomic uracil and a distinct AID mutational signature. DNA Repair. 2015;25:60–71. doi: 10.1016/j.dnarep.2014.11.006. [DOI] [PubMed] [Google Scholar]
- 79.Kakushadze Z., Yu W. How to combine a billion alphas. J. Asset Manag. 2017;18(1):64–80. Available online: http://ssrn.com/abstract=2739219. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.