Continuous track paths reveal additive evidence integration in multistep decision making

Significance

Many daily-life decisions consist of multiple steps (e.g., go outside, go left, arrive at Italian restaurant). We distinguish four prominent models of such multistep decision making. We further propose a paradigm in two experiments to disentangle these models. Only the models implementing additive integration from second- to first-step choices were able to account for track path movements. Specifically, we find that first-step decisions are initially based on the sum/mean of second-step future rewards. As information regarding the optimal second-step choice increases, the decision gradually becomes based on the maximal future reward. Hence, we suggest that multistep decision making involves progressive unraveling of future outcomes during decision making.

Abstract

Multistep decision making pervades daily life, but its underlying mechanisms remain obscure. We distinguish four prominent models of multistep decision making, namely serial stage, hierarchical evidence integration, hierarchical leaky competing accumulation (HLCA), and probabilistic evidence integration (PEI). To empirically disentangle these models, we design a two-step reward-based decision paradigm and implement it in a reaching task experiment. In a first step, participants choose between two potential upcoming choices, each associated with two rewards. In a second step, participants choose between the two rewards selected in the first step. Strikingly, as predicted by the HLCA and PEI models, the first-step decision dynamics were initially biased toward the choice representing the highest sum/mean before being redirected toward the choice representing the maximal reward (i.e., initial dip). Only HLCA and PEI predicted this initial dip, suggesting that first-step decision dynamics depend on additive integration of competing second-step choices. Our data suggest that potential future outcomes are progressively unraveled during multistep decision making.

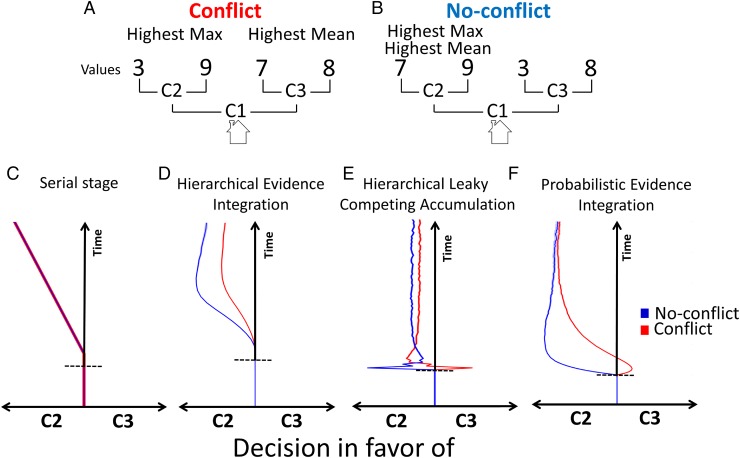
Imagine leaving your house in search of food in the neighborhood. Outside, you must first decide to go left or right. Going left subsequently affords a second left–right choice between Thai and Italian food, whereas going right affords another left–right choice between Mexican and Lebanese food. This illustrates a typical two-step tree path decision-making scenario (i.e., four potential tree paths; see Fig. 1A). Such two-step decisions have been conceptualized within the framework of model-based reinforcement learning (1, 2), and recent work has focused on which brain areas underpin reward representation in multistep decision making (3–5). However, the computations underlying multistep decision making are still debated. To address this issue, we distinguish four computational models. We derive and contrast empirical predictions from the four models and test them. In the following paragraph we explain the common ideas and distinguishing features of the four models.

Fig. 1.

(A) Conflict trial. The highest mean of potential rewards is associated with going right at C₁ (i.e., toward C₃, the nonoptimal choice), whereas the highest maximal reward is associated with going left at C₁ (i.e., toward C₂, the optimal choice). (B) No-conflict trial. Both the highest mean of potential rewards and the highest maximal reward are associated with going left at C₁ (i.e., toward C₂, the optimal choice). (C) The serial stage model. The decision dynamics for both conflict (red line) and no-conflict (blue line) trials throughout the trial are drawn toward the optimal choice. Note that both decision patterns overlap (we increased line width of the conflict dynamics for figure clarity). (D) The HEI model. The dynamics of both trial types throughout the trial are drawn toward the optimal choice, but with a stronger bias for no-conflict compared with conflict trials. (E) The HLCA model. The dynamics of conflict trials display an initial dip before shifting toward the optimal choice. The dynamics of no-conflict trials throughout the trial are biased toward the optimal choice. Note that at some point the dynamics of no-conflict trials display a drop-off. (F) The PEI model. The dynamics of conflict trials display an initial dip before shifting toward the optimal choice. For no-conflict trials, the dynamics throughout the trial are biased toward the optimal choice. No-conflict trials are always more biased toward the optimal choice compared with conflict trials. The horizontal dashed lines indicate the stimuli onset point. Full lines in C–F are averages across 100 simulations; shaded areas represent ±1 SE.

In each model, each tree path is associated with an evidence (E) accumulator (e.g., in Fig. 1A, there are four tree paths; we will use Fig. 1A and Supporting Information, Appendix A: Computational Models, Fig. S1, to illustrate the four models). The two leftmost E accumulators (i.e., leading to 3 and 9 in Fig. 1A) are taken as inputs to a left motor evidence (ME) accumulator. The two rightmost E accumulators project to a right ME accumulator. All models reach decisions by gradually updating their E and/or ME accumulator values at each iteration depending on the rewards associated with each tree path. Models can be conceptually distinguished based on three features. The first feature—mapping—defines how E accumulators map to ME accumulators; in particular, this feature distinguishes models where only the maximally active E accumulator projects to its correspondent ME accumulator [i.e., max-based mapping] from models where the (weighted) sum of E accumulators project to their corresponding ME accumulators (i.e., additive-based mapping). The second feature determines the amount of temporal overlap between activity at the E and ME levels. The third feature concerns the interaction between E or ME accumulators. In particular, E/ME accumulators can race independently (2) or interact (e.g., via lateral inhibition) in some way (6, 7). We now describe the four models in terms of these three features.

In the serial stage model (Supporting Information, Appendix A: Computational Models, Fig. S1A), first, the mapping from E accumulators to ME accumulators is max-based; only the maximally active (here, two) E accumulators feed activation into their ME accumulator (feature 1; mapping). Second, it imposes a strict temporal separation between E accumulation and ME accumulation (hence its name) (feature 2; overlap). During decision making, each tree path accumulates evidence with a constant rate defined by its total reward outcome (the higher the reward, the higher the rate). When a competitor crosses a decision boundary, the decision is made and the associated reward selected (i.e., E stopping criterion). At this point, the winning E accumulator projects to its corresponding ME accumulator. When the difference between ME accumulators reaches a second threshold, the decision is implemented (i.e., ME stopping criterion). The same ME stopping criterion is used in all following models. Third, there is no interaction between E accumulators or between ME accumulators (feature 3; interaction).

The hierarchical evidence integration (HEI) (Supporting Information, Appendix A: Computational Models, Fig. S1B), first, implements max-based mapping between E and ME accumulation. Second, and like all following models, HEI allows more temporal overlap between E and ME accumulation (8–10). Once either one of the two leftmost (rightmost) E accumulators reaches a threshold, the maximal leftmost (rightmost) E accumulator projects to the left (right) ME accumulator. However, the losing E accumulator is not pruned away and can potentially feed into its corresponding ME accumulator: For example, if at time t₁ of the decision process the E_L,L accumulator (subindices indicate the left at C₁ and left at C₂ pathway; see Fig. 1A) is higher than that for E_L,R, the E_L,L accumulator feeds into the left ME accumulator. However, if at time t₂ (>t₁) E_L,R > E_L,L, the E_L,R accumulator feeds into the left ME accumulator. Third, there is no interaction between E accumulators or between ME accumulators.

In the hierarchical leaky competing accumulator (HLCA) (Supporting Information, Appendix A: Computational Models, Fig. S1C) model, first, the mapping between E and ME accumulators is additive-based: ME accumulators receive additive input from their E accumulators. Second, there is complete temporal overlap between E and ME accumulation; i.e., E accumulators feed ME accumulators from the very beginning of the decision process. Third, E accumulators connected to the same ME accumulator interact via lateral inhibition, and ME accumulators do not interact.

Finally, we envisage the probabilistic evidence integration (PEI) (Supporting Information, Appendix A: Computational Models, Fig. S1D) model (6). The PEI model reformulates the decision-making problem in terms of generative probabilistic inference (11, 12). Specifically, a generative model defines how situations, plans, actions, and outcomes interact to generate reward (6). Decision making is solved through inverse inference of this generative model. The reward is treated as given (i.e., conditioned upon), and the decision process amounts to computing which action best predicts this reward occurrence. Decision making consists of selecting the action that maximizes the probability of observing the reward. Here, left E accumulators reflect the left–right choice probabilities at C₂, right E accumulators reflect the choice probabilities at C₃, and ME accumulators reflect choice probabilities at C₁ (Fig. 1A and Supporting Information, Appendix A: Computational Models, Fig. S1D). Because of this probabilistic formulation, the expected rewards associated with ME accumulators are defined by the probability-weighted sum of their corresponding E-accumulator rewards. For example, in Fig. 1A the rewards associated with left E accumulators are, respectively, 3 and 9. At the start of the decision process the choice probabilities linked to each left E accumulator are uniform (i.e., 0.5 each). Thus, the expected reward of the left ME accumulator is approximated by the mean of its E accumulator rewards (0.5 × 3 + 0.5 × 9). When choice probabilities of left E accumulators become more refined (i.e., as posteriors are updated), the left ME accumulator expected reward is approximated by the maximal reward of E accumulators (0 × 3 + 1 × 9). Therefore, first, the mapping between E and ME accumulators is additive. At every iteration, these choice probabilities are updated according to Bayes’ rule (Supporting Information, Appendix A: Computational Models). Second, there is complete temporal overlap between E and ME accumulation because all probabilities are updated at every step. Third, probabilities are normalized at every step [e.g., p(π_L|C₁,r) + p(π_R|C₁,r) = 1; Supporting Information, Appendix A: Computational Models], which implicitly defines an interaction between left E accumulators, between right E accumulators, and between ME accumulators.

We devised a paradigm to disentangle these four models. Consider again the initial food search example. Imagine that turning left affords you two types of food that you value, respectively, at 3 and 9, whereas turning right affords you foods that you value, respectively, at 7 and 8 (Fig. 1A). Hence, turning right is associated with the highest mean between reward outcomes. In contrast, turning left is associated with the maximal reward. We call this a (mean-max) conflict trial (as in ref. 6). Instead, imagine food reward values of 7 and 9 when you turn left and 3 and 8 when you turn right (Fig. 1B). In this no-conflict trial, the choice “turning left” is associated with both the highest mean and the maximal reward. The serial stage, HEI, HLCA, and PEI models predict distinct first-step (i.e., at C₁) decision dynamics in conflict versus no-conflict trials when participants eventually select the accurate optimal choice (i.e., leading to the maximal reward; Fig. 1 C–F). We clarify each model’s dynamics and behavioral predictions below (see Supporting Information, Appendix A: Computational Models, for a full explanation and equations). We tested these predictions in two experiments: in a button-press task and a reaching task (e.g., ref. 13). Participants were shown two potential rewards linked to a first-left choice and two potential rewards linked to a first-right choice. In a subsequent second step, participants chose between the two potential rewards linked to their first choice (Fig. 2 A and B).

Fig. 2.

(A) Button-press task design. Participants had to press the left–right button if they decided to select the left–right reward(s). At the first step, they decided between two of four potential rewards. At the second step, they selected one of the previously two selected rewards. Optimal button-press choices are illustrated by black hands. (B) Reaching task design. Participants had to reach for the left–right target if they decided to select the left–right option. When participants crossed the onset point (OP; see Top Left example), numbers were displayed on the screen. The dashed lines in the figure illustrate optimal reach choices.

The button-press task was used to check basic psychometric properties of the task and fit parameters of all models. It also tested whether conflict trials are slower than no-conflict trials, as predicted by the HEI, HLCA, and PEI models (Supporting Information, Appendix A: Computational Models). The reaching task tested the main prediction of our study. First, the serial stage model predicts no trajectory (i.e., decision dynamics) differences for conflict and no-conflict trials (Fig. 1C). For both trial types, the decision dynamics are biased toward the optimal choice throughout the entire trial time course. Second, the HEI model predicts that the decision dynamics of both trials are biased toward the optimal choice. However, the bias is stronger for no-conflict than for conflict trials (Fig. 1D). Third, the HLCA model predicts that the decision dynamics are different for both trial types. Whereas the no-conflict trials are throughout the entire time course biased toward the optimal choice, the conflict trials are initially biased toward the nonoptimal choice (Fig. 1E). This initial bias will from now on be called “an initial dip.” Fourth, like the HLCA, the PEI model also suggests that decision dynamics initially dip toward the nonoptimal choice for conflict trials before being redirected toward the optimal choice. No-conflict trials throughout the trial are biased toward the optimal choice (Fig. 1F). Furthermore, the bias toward the optimal choice is always stronger for no-conflict than for conflict trials.

Results

Button-Press Task.

The 2 (trial type: conflict, no-conflict) × 5 (quantiles) repeated-measures ANOVA revealed main effects of conflict and quantiles both for accuracy [F(1,14) = 33.4, P < 0.001, and F(4,56) = 5.2, P < 0.01] and reaction times (RTs) [F(1,14) = 59.9, P < 0.001, and F(4,56) = 446.8, P < 0.001]. We further observed a significant interaction between both factors in accuracy [F(4,56) = 4.1, P < 0.01] and RTs [F(4,56) = 12.3, P < 0.001]. These results reveal a mean-max conflict effect, whereby conflict trials are slower and less accurate compared with no-conflict trials (see Supporting Information, Appendix A: Computational Models for model predictions). Moreover, the interaction reveals that the difference in accuracy between conflict and no-conflict trials decreases as RTs become slower. The difference in RTs increases as RTs become slower (Fig. 3A).

Fig. 3.

Button-press task results: (A, Upper graph) Bin analysis for accuracy of conflict (red) and no-conflict (blue) trials. Accuracy was higher for no-conflict compared with conflict trials at all bin levels. The difference in accuracy between trial types decreases as RTs slow down. (A, Lower graph) Bin analysis for RTs of conflict (red) and no-conflict (blue) trials. Conflict trials lead to higher RTs compared with no-conflict trials at all bin levels. The difference in RTs between trial types increases as RTs slow down (***P < 0.001, **P < 0.01). Reaching task results: (B) Average reach trajectories (collapsed across left and right reaches) toward the optimal target (OT) for conflict (red lines) and no-conflict (blue lines) trials. The red vertical bar shows when, during the reach conflict trials, choices significantly deviated toward the nonoptimal choice. (C) Illustrations of single conflict (red lines) and no-conflict (blue lines) trajectories in four randomly chosen subjects (note, however, that all subjects display the patterns revealed in these illustrations). (D) Percentage of trials favoring the optimal choice as a function of normalized time for both conflict (red line) and no-conflict (blue line) trials. The red horizontal bar indicates where the percentage of trials favoring the optimal choice significantly dips below 50% for conflict trials. Error bars in A, as well as shaded areas in B and D, indicate the SEM.

Reaching Task.

Fig. 3B shows the mean path trajectories (i.e., decision dynamics) for conflict (red lines) and no-conflict (blue lines) trials. Mean conflict trajectories initially dip toward the nonoptimal choice target before being redirected toward the optimal choice target. One-sample t tests on trajectories’ x-dimension positions revealed a significant deviation toward the nonoptimal choice target from time steps 43–63 in conflict trials. Illustrative single-trial initial dips are shown in Fig. 3C. Conflict trials deviate toward the target representing the nonoptimal choice target before being redirected toward the target representing the optimal choice (red lines). In contrast, no-conflict trajectories are throughout the trial biased toward the optimal choice target (blue lines). Furthermore, cross-validating the trajectory data, Fig. 3D displays the percentage of trials favoring the optimal choice as a function of normalized time for both the conflict (red line) and the no-conflict trials (blue line). Crucially, one-sample t tests revealed that the percentage of trials favoring the optimal choice as a function of time initially dipped significantly below 50% in conflict trials from time steps 39–57. This never occurs in no-conflict trials.

Both the HLCA (Fig. 1E) and PEI (Fig. 1F) models predict the initial dip observed in the data (Fig. 3B). This is due to the additive mapping from E to ME accumulators (feature 1; mapping), which appears crucial to account for (this aspect of) multistep decision making.

The initial dip in conflict trials, alternatively, may be explained by an attentional account, whereby participants may have initially randomly sampled number stimuli one at a time. Under this assumption, one could argue that conflict trials, displaying higher rewards associated with the nonoptimal choice compared with the no-conflict trials, would also induce an initial dip toward the nonoptimal choice. Such an alternative explanation can easily be implemented within the HEI framework (Supporting Information, Appendix A: Computational Models). We simulated two versions of this alternative explanation. The first simulation was performed with best-fit parameters of the HEI model (Supporting Information, Appendix A: Computational Models, Fig. S7A). The second simulation was performed with parameter settings that maximize the chances of observing the initial dip (Supporting Information, Appendix A: Computational Models, Fig. S7B). Neither of these two versions of the alternative explanation predicts an initial dip for conflict trials. Furthermore, implementing the attentional account within the serial stage model will never predict the initial dip because the decision process is implemented at the E-level accumulation (Supporting Information, Appendix A: Computational Models). This implies that the serial stage model will always induce similar decision dynamics (i.e., reach predictions) for conflict and no-conflict trials.

Discussion

A reaching task was designed to test the predictions of the serial stage, HEI, HCLA, and PEI models in multistep decision making. Mean path trajectories dipped toward the nonoptimal choice early in the trajectory before being redirected toward the optimal choice. This initial dip feature was present in the HLCA and PEI models. Therefore, the data refute the serial stage and HEI models. We suggest that additive integration (feature 1; mapping) from E to ME accumulators is a prominent model feature. The HLCA model proposes that evidence integration of immediate choices is based on a continuous input of potential future rewards that compete with one another. The PEI model suggests that expected rewards of immediate choices are initially approximated by the mean of potential future rewards. As more information becomes available, the inferred expected reward of each immediate choice is gradually represented by the maximal reward available following that choice. Both models describe a transition from the sum (HLCA) or the mean (PEI) of rewards to the maximal reward as driving evidence integration during the decision process.

To disentangle the several multistep decision-making models, three paradigm attributes were crucial. First, we needed a multistep decision-making design. Indeed, in standard (single-step) experimental designs using, for example, a constant coherence percentage of a random dot motion display (9, 10, 14) or single-step reward values (15), serial stage/HEI and HLCA/PEI models are not easily distinguishable (6). Second, in a multistep decision-making design, we needed mean-max conflict trials. In Solway and Botvinick’s (2) multistep design, conflict trials occurred less than 3%. Third, we needed a reaching task to track the subject’s hand position online (for a review on the use of reaching tasks for testing cognitive theories, see ref. 16).

Because they implement additive-based accumulation, both the HLCA and PEI predict an initial dip toward the nonoptimal choice before shifting back toward the optimal choice in conflict trials (Supporting Information, Appendix A: Computational Models, Fig. S1 C and D). Both HLCA and PEI also allow full temporal overlap between E and ME accumulation. Although the models are similar in these two features, the models did make slightly different predictions (Fig. 1 E and F and Supporting Information, Appendix A: Computational Models). The reason for this divergence is that the interaction (competition) between E (and ME for the PEI) accumulators was implemented differently in the two models. Interaction was based on mutual inhibition in the HLCA (at the E-accumulator level) and on choice probability normalization (at the E- and ME-accumulator levels) in the PEI. These differences need to be exploited in further work to potentially disentangle both models.

Despite the traditional connection in the literature between probabilistic and normative models, we do not consider the PEI model as a normative model. Instead, it is used as a tool to implement a specific decision-making hypothesis (17), consisting of at least three features, of which perhaps the most important one is that E accumulators are initially (i.e., early during decision making) averaged.

We foresee at least three advantages of this additive feature in multistep decision making. First, it allows a fault-tolerant online construction of the decision tree. Indeed, when adding or averaging potential future rewards, the system can initially function appropriately even when later decision paths are “entwined” (i.e., generated in their inappropriate path location). For example, Fig. 1A shows a decision tree affording a choice between 3 (left–left path), 9 (left–right path), 7 (right–left path), and 8 (right–right path). The first response will still be correct in case the agent initially generates a wrong tree such as 9 (left–left path), 3 (left–right path), and 8 (right–left path), and 7 (right–right path) before generating the correct one. Such a system allows coping in real time with the multitude of sequential decisions in natural environments and ultimately generates deep decision trees. Second, decisions must sometimes be made with limited cognitive resources, for example, due to strict time limits. In such conditions, a valid option is to chunk (add or average) future rewards and base an initial decision on this computation. When environmental constraints are more lenient and allow additional processing time, a more refined option can be computed and lead the decision maker toward the maximal reward. Hence, a trade-off exists between a costly evidence integration process and obtaining a maximal reward (18). Third, in natural environments the choice reflecting the maximal reward and the choice reflecting the maximal average or addition of rewards will often be the same. In such circumstances, it is advantageous to have the decision dynamics initially attracted toward the choice with the highest sum or mean value.

By way of comparison, the human visual system can represent a large number of peripheral features in a single representation known as a “visual ensemble” (19, 20). We propose that a similar process occurs in multistep decision making. In particular, just as one averages stimuli far away from the focus of attention in visual perception, one similarly averages stimuli “far away” (i.e., the future rewards of late decision steps) from the current focus of decision in multistep decision making. In line with this proposal, humans can extract ensemble statistics from a variety of features and stimuli, including size (21, 22), speed (23), position (24), spatial orientation, and frequency, even under reduced attention (25). Furthermore, ensemble averaging is not limited to low-level perceptual stimuli. Humans can efficiently extract the average gender or emotion from a set of faces (26–28). Crucial for our proposal, ensemble averaging is also possible with symbolic stimuli: Humans can efficiently extract the mean value of a set of number stimuli (29, 30).

LCA models have also been applied to value-based (31, 32), perceptual (33, 34), lexical (35), and multialternative (36) decision making. Similarly, generative models have been applied to several aspects of cognition including concept learning (37), causal learning (38, 39), motor control (40, 41), and perception (42). In the present work, we further tested and provided evidence suggesting that the computations involved in LCA (i.e., HLCA) and generative (i.e., PEI) models can be applied to multistep decision making (43). Specifically, evidence integration in multistep decision making is initially defined by the sum/mean value of future potential rewards. Future research should aim to disentangle these models. For example, such research could focus on investigating how priors may be influenced by motivational (44), temporal (45), or emotional (46) factors. Furthermore, research in multistep decision making should also focus on assessing how the representations of ensemble statistics are neurally coded and evolve to bias decisions.

Materials and Methods

Participants.

Fifteen (10 females, mean age = 22.1 and SD = ±2.1) and 20 (13 females, mean age = 22.5 and SD = ±3.2) subjects, respectively, participated in the button-press and reaching tasks in exchange for monetary compensation, and all provided written informed consent. Experiments were approved by the local ethics committee (Faculty of Psychology, Université Libre de Bruxelles).

Experimental Designs and Stimuli.

In the button-press task (Fig. 2A), participants were instructed to perform two speeded consecutive choices. In the first step, participants chose between two potential upcoming choices, each associated with two potential monetary rewards. In the second step, participants chose between the potential rewards selected in the first step. Participants first saw a fixation cross at the center of the screen (1,500 ms). Subsequently, the four numbers forming the first-step choice appeared surrounding the fixation. Participants were instructed to press on the side of the optimal decision (i.e., leading to the maximal reward) as fast as possible (speed limit of 1,500 ms). The first-step choice was followed by a jittered interchoice interval (ICI) randomly selected from a uniform distribution ranging from 700 to 900 ms in steps of 50 ms. The ICI was immediately followed by the second-step choice and ended upon button press or time limit (1,500 ms). Button presses were recorded with the RB-834 Cedrus response box. The participants’ task was to gain as much money as possible by making optimal choices (i.e., leading to the maximal reward). They were informed that the magnitude of the selected second-step number was proportional to real monetary reward (in euros). Every 16 trials, participants received feedback indicating how much money had accumulated up to that point. To keep them highly motivated, participants were told that their monetary compensation would amount to their total accumulated money. However, in the end they all received the same monetary compensation.

The reaching task was similar with the following differences (Fig. 2B). Each trial started when participants touched (with a cordless pen) the start square at the bottom of the screen, triggering the appearance of a fixation cross midway between left and right targets. Participants were instructed to start moving toward the fixation cross as soon as it appeared. When the y coordinate was above 110 [i.e., the onset point, 13% of the total reach distance (y dimension) between the start square and the target], the four numbers forming the first-step choice appeared on screen, and participants had to reach the target corresponding to the optimal reach choice as fast as possible. To enforce speeded reaches, a time limit of 1,500 ms was implemented. To begin the second-step choice, participants had to press the start square again. The second-step choice unfolded exactly as the first-step one, with the exception that the two selected first-step numbers were randomly displayed to the left and right of the fixation cross. Participants were told that, if they stopped moving or lifted the pen at any point during the reach, the trial would be counted as null and a “do not stop”/“do not lift the pen” sign would appear in the middle of the screen. Movement trajectories were recorded with a Wacom LCD tablet DTF-720 sampling trajectory coordinates at 60 Hz. Both tasks were implemented on Matlab using the psychtoolbox 3 (47), and the screen resolution was 800 × 600.

Each experiment started with a training block of 16 trials. Subsequently, participants performed three blocks of 199 trials. Each block comprised 96 conflict, 96 no-conflict, and 7 (3.5%) catch trials (see below) that were randomly presented. Optimal choice side and number positions in the first-step choice were fully counterbalanced.

Stimuli (i.e., potential rewards) were numbers ranging from 1 to 9. Catch trials contained numbers from 10 to 13. These trials were included to prevent participants from choosing based solely on physical features of the highest potential reward (i.e., the features of the number 9). In the first-step choice, stimuli were presented on the four corners of a virtual rectangle centered on the fixation cross (width: 70 pxl; height: 40 pxl). The two stimuli on the left of the fixation cross represented the left choice, whereas the two stimuli on the right of the fixation cross represented the right choice. Difficulty overall was similar in both trial types (Supporting Information, Appendix B: Trial Types and Difficulty, Fig. S13).

Data Analysis: Button Press Task.

Because model predictions concern first-step choices, button-press RTs were analyzed only for the first-step optimal choices. RTs faster than 100 ms were discarded from the analysis. To approximate the decision dynamics, RTs were binned into five quantiles, and we performed a 2 (trial type: conflict, no-conflict) × 5 (quantiles) repeated-measures ANOVA on accuracy, as well as RTs.

Data Analysis: Reaching Task.

For the same reasons as in the button-press task, reach trajectories were analyzed only for the first-step optimal choices. We discarded all data points (i.e., x and y reach positions) before the stimuli onset point. Additionally, trajectory time was normalized to facilitate trajectory comparison between trials with different movement times and to reduce interindividual variability. Specifically, the duration of every reach was sliced into 101 time bins of identical length (13, 48, 49). Furthermore, to compare empirical trajectories with the model decision dynamics displayed in Fig. 1 C–F, we collapsed right-reach onto left-reach trajectories. All subsequent analyses were performed on the normalized trajectories. To test the decision dynamics and assess whether conflict trajectories would initially dip toward the nonoptimal choice, we plotted the mean normalized trajectories. If conflict trials initially dip toward the nonoptimal choice, mean conflict trajectories should deviate toward the nonoptimal choice target (i.e., away from the midline between both choice targets) before being redirected toward the optimal choice. We then performed a one-sample t test against the average first time point (of the 101 normalized time points) x-dimension position value and reported at which time point the trajectories significantly deviated toward the nonoptimal choice for no-conflict and conflict trajectories. In addition to the average (x and y) positions at each time point, we computed the percentage of trials favoring the optimal choice as a function of time. Similarly, we performed a one-sample t test against 50% (baseline value) at every time point. If the decision dynamics are initially biased toward the nonoptimal choice, the percentage of trials favoring the optimal choice should initially dip below 50% before going to 100% (the optimal value). Likewise, we report at which time point this percentage dips significantly below 50% for both trial types.

Model-Fitting Procedure.

Models were fitted using differential evolution as implemented in the DeMat Matlab toolbox [default implementation (50)]. The fitting procedure was similar to Solway and Botvinick (2). Each generation comprised 10 times the number of free parameters in the model, and the entire data set was simulated for every combination of the parameters (i.e., population member). Given the stochasticity in differential evolution, the optimization procedure was repeated 10 times, and the best-fit parameters were retained. The objective function consisted of the residual sum of squares of the group psychometric accuracy curves of the button-press experiment (Fig. 3A, Upper graph). Accuracy was fitted because it is unclear how accuracy should be weighted relative to RT. Moreover, this procedure allowed us to test how well a specific parameter configuration generalized beyond accuracy to the main variable of interest (i.e., trajectories; see Supporting Information, Appendix A: Computational Models for button-press task RT and accuracy predictions) (51). The optimization process was stopped when parameters displayed identical values for 100 consecutive generations. Best-fit parameters for each model are reported in Supporting Information, Appendix A: Computational Models, Table S1.