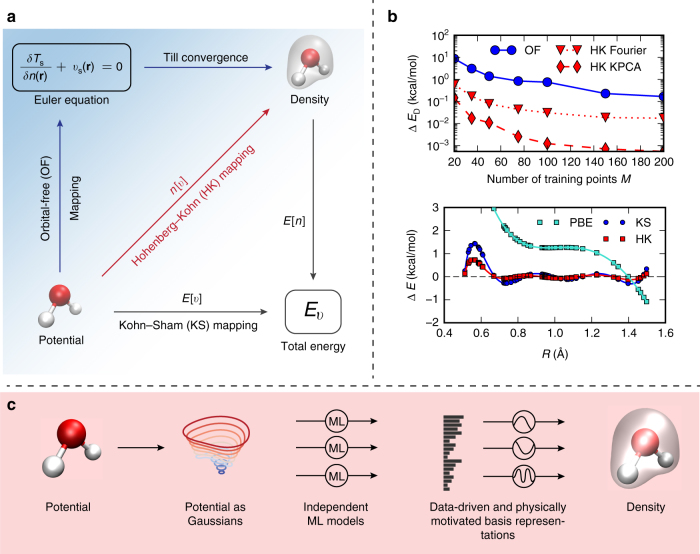
Fig. 1.

Overview of approach and motivation. a Mappings used in this paper. The bottom arrow represents E[v], a conventional electronic structure calculation, i.e., KS-DFT. The ground-state energy is found by solving KS equations given the external potential, v. E[n] is the total energy density functional. The red arrow is the HK map n[v] from external potential to its ground state density. b (Top) How the energy error depends on M, the number of training points, for ML-OF and ML-HK with different basis sets for the 1D problem. b (Bottom) Errors in the PBE energies (relative to exact values) and the ML maps (relative to PBE) as a function of interatomic spacing, R, for H₂ with M = 7. c How our Machine Learning Hohenberg–Kohn (ML-HK) map makes predictions. The molecular geometry is represented by Gaussians; many independent Kernel ridge regression models predict each basis coefficient of the density. We analyze the performance of data-driven (ML) and common physical basis representations for the electron density