Bayesian variable selection for a semi-competing risks model with three hazard functions

Abstract

A variable selection procedure is developed for a semi-competing risks regression model with three hazard functions that uses spike-and-slab priors and stochastic search variable selection algorithms for posterior inference. A rule is devised for choosing the threshold on the marginal posterior probability of variable inclusion based on the Deviance Information Criterion (DIC) that is examined in a simulation study. The method is applied to data from esophageal cancer patients from the MD Anderson Cancer Center, Houston, TX, where the most important covariates are selected in each of the hazards of effusion, death before effusion, and death after effusion. The DIC procedure that is proposed leads to similar selected models regardless of the choices of some of the hyperparameters. The application results show that patients with intensity-modulated radiation therapy have significantly reduced risks of pericardial effusion, pleural effusion, and death before either effusion type.

1. Introduction

Global cancer incidence estimates from 2008 indicate that esophageal cancer is the eighth most common and the sixth most deadly among cancers [2]. Torrey et al. [3] estimated that there were 455,800 new cases and 400,200 deaths in 2012. The two most common types of esophageal cancer are squamous cell carcinoma and adenocarcinoma, the latter of which has been linked to obesity and gastrointestinal problems. Definitive concurrent chemoradiotherapy (CRT) is the standard treatment for esophageal cancers for patients with inoperable tumors. Several different methods for delivering radiation are used, particularly three dimensional conformal radiation therapy (3D-CRT). All of these methods increase patient survival but also have several adverse effects, the most common being pleural effusion (PE) and pericardial effusion (PCE) [4] [5]. Pleural and pericardial effusion occur when excess fluid is present around the lungs and heart, respectively, and can lead to poor function of these organs and death. These adverse events are associated with higher doses of radiation to the heart and lungs [5].

Intensity-modulated radiation therapy (IMRT) has been shown to reduce the volume of a patient’s non-cancerous organs exposed to radiation and increase volume of radiation on esophageal tumors compared to 3D-CRT [6]. Chandra et al. [7] showed that IMRT reduced the volume of lungs that received different radiation doses compared to 3D-CRT. Due to the relationship between increased dosage and effusion rates, IMRT potentially could result in fewer incidences of pleural and pericardial effusion in esophageal cancer patients compared to standard 3D-CRT treatment. Assessing the impact of IMRT on time to effusion is more complicated than assessing the impact of IMRT on overall survival time, even when pleural and pericardial effusion are considered separately. When the survival time of interest is a non-terminal event such as effusion, death is commonly assumed to be a non-informative independent censoring event [8]. This assumption is invalid because both pleural and pericardial effusion could lead to death, which means that death may indicate that a patient experienced effusion, which is informative censoring. Another complication with this data structure is that patients can experience effusion followed by death, but not death first and effusion afterwards. Administrative right censoring could occur before a patient experiences either event type or after a patient has effusion. Due to these complications, this data structure must be analyzed with a semi-competing risks model. This model has different hazards for three events: a given non-terminal event, death before the non-terminal event and death after the non-terminal event.

Lee et al. [9] developed a novel Bayesian semi-parametric semi-competing risks regression model for a non-terminal event and death. Their motivating non-terminal event of interest was hospital readmission for patients diagnosed with advanced pancreatic cancer. Since pancreatic cancer has high mortality rates, they were concerned with end of life care and keeping patients comfortable at home during their final days. They considered three different hazard functions: the hazard of a non-terminal event, the hazard of death without a non-terminal event, and the hazard of death after a non-terminal event. Each of these three hazard functions resembled a Cox-type regression including a baseline hazard function which was assumed to be piecewise exponential, individual patient frailty parameters, and a linear combination of patient covariates. They used the posterior sample of the beta coefficients in the three hazards for inference on what types of homecare affected the hazard that a patient would return to the hospital, the hazard of death before returning to the hospital, and the hazard of death after patients were readmitted to the hospital. They implemented their algorithm in the package SemiCompRisks [10].

We initially aimed at implementing the semi-competing risks model of Lee et al. [9] to analyze the effects of IMRT on effusion and overall survival for an observational study consisting of 470 patients at The University of Texas M.D. Anderson Cancer Center in Houston, TX, treated between January 1998 and April 2012 [11]. However, it was unclear which baseline covariates should be included in the model for analyzing the IMRT effect, particularly because of the correlation between treatment group assignment and the baseline covariates, which could affect clinical conclusions. Consequently, in this paper we develop a variable selection procedure for the semi-competing risks model of Lee et al. that uses spike-and-slab priors and stochastic search variable selection (SSVS) algorithms for posterior inference. The proposed procedure performs variable selection for each of the linear terms in the three hazard functions. Furthermore, we devise a protocol to choose the threshold on the marginal posterior probability of variable inclusion based on the Deviance Information Criterion (DIC). The code for the described methodology can be found in the R package SCRSELECT [1] In the application to the data from the esophageal cancer patients we do not perform variable selection on the IMRT status. To correct for some of the bias introduced in a nonrandomized observational study, we estimate the probability of receiving IMRT for each patient as a function of other covariates and include this propensity score in each hazard function. This allows us to compare the effects of IMRT on effusion and death while correcting for bias for non-randomization in every potential model. We present results from analyses done separately for pleural and pericardial effusion, where we show how the DIC procedure we propose leads to similar selected models, regardless of the choice of some of the hyperparameters. We find that patients with IMRT radiation have significantly reduced risks of pericardial effusion, pleural effusion and death before either effusion type. The rest of the paper is organized as follows: In section 2, we describe the Bayesian semi-parametric semi-competing risks model, the variable selection priors and the Markov Chain Monte Carlo procedure for posterior inference. We also present the DIC-based procedure that we propose for the final covariate selection. In section 3, we perform a simulation study to assess our proposed DIC-based procedure. In section 4, we describe the case study data and discuss results and sensitivity to hyperparameter choices. Section 5 concludes the paper with a discussion.

2. Methods

2.1. Semi-Parametric Semi-Competing Risks Model

Let T_1i denote the time to a non terminal event and T_2i be the time to death for patient i. Lee et al. [9] model covariate effects in the three hazard functions in the following manner. They denote h₁, the hazard of a non-terminal event, h₂ the hazard of a terminal event when the non-terminal event has not occurred and h₃, the hazard of a terminal event after the non-terminal event has occurred. Let x_i denote the vector of patient covariates and β₁, β₂, β₃ denote the three coefficient vectors associated with x_i in hazards 1,2, and 3, respectively. They list the functional forms of the three hazards for the semi-markov model as

$$h_1(T_{1i}\mid {\gamma }_i,{\beta }_{\mathbf{1}},x_i)={\gamma }_i{h}_{01}(T_{1i})exp(x_i^t{\beta }_{\mathbf{1}}),$$ (1)

$$h_2(T_{2i}\mid {\gamma }_i,{\beta }_{\mathbf{2}},x_i)={\gamma }_i{h}_{02}(T_{2i})exp(x_i^t{\beta }_{\mathbf{2}})$$ (2)

and

$$h_3(T_{2i}\mid T_{1i},{\gamma }_i,{\beta }_{\mathbf{3}},x_i)={\gamma }_i{h}_{03}(T_{2i}-T_{1i})exp(x_i^t{\beta }_{\mathbf{3}}).$$ (3)

γ_i is the frailty for patient i and h_0g is the baseline hazard function for event g = 1, 2, 3. Even though here, we consider the same set of covariates for each of the three hazards, model formulation (1)–(3) can accommodate different lists of covariates for each hazard function. Lee et al. [9] assume that the log baseline hazard functions are piecewise exponential, that is λ_g,j = log(h_0g(t)) is constant for t ∈ I_g,j = (s_g,j−1, s_g,j] for a partition of the time scale s_g,0 = 0 < s_g,1 < s_g,2 < … < s_g,Jg < s_g,max, where s_g,max is the largest observed time for event g. The observed events are Y_1i = min(T_1i, T_2i, C_i), δ_1i = I[T_1i ≤ min(T_2i, C_i)], Y_2i = min(T_2i, C_i) and δ_2i = I[T_1i ≤ C_i]. These are realizations of T_1i, the time to non terminal event, T_2i, the time to death, and C_i, the independent censoring time for patient i. The likelihood for this parameterization of the baseline hazard functions and given hazard functions (1)–(3) is

$$\begin{array}{c}L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{1}},{\beta }_{\mathbf{2}},{\beta }_{\mathbf{3}},\gamma ,{\mathbf{s}}_{\mathbf{1}},{\mathbf{s}}_{\mathbf{2}},{\mathbf{s}}_{\mathbf{3}},{\lambda }_{\mathbf{1}},{\lambda }_{\mathbf{2}},{\lambda }_{\mathbf{3}})=\\ \prod _{j=1}^{J_1+1}\prod _{k=1}^{J_2+1}\prod _{l=1}^{J_3+1}exp\{{\lambda }_1{d}_{1j}-exp({\lambda }_{1k})\sum _{m\in {\mathcal{R}}_{1j}}{\mathrm{\Delta }}_{mj}^1{\gamma }_{m}exp(x_m^t{\beta }_{\mathbf{1}})\}\times exp\{{\lambda }_2{d}_{2k}-exp({\lambda }_{2k})\sum _{q\in {\mathcal{R}}_{2k}}{\mathrm{\Delta }}_{qk}^2{\gamma }_{q}exp(x_q^t{\beta }_{\mathbf{2}})\}\\ \times exp\{{\lambda }_3{d}_{3l}-exp({\lambda }_{3l})\sum _{r\in {\mathcal{R}}_{3l}}{\mathrm{\Delta }}_{rl}^3{\gamma }_{r}exp(x_r^t{\beta }_{\mathbf{3}})\}\times \prod _{m^{\prime }\in {\mathcal{D}}_{1j}}{\gamma }_{m^{\prime }}exp(x_{m^{\prime }}^t{\beta }_{\mathbf{1}})\prod _{q^{\prime }\in {\mathcal{D}}_{2k}}{\gamma }_{q^{\prime }}exp(x_{q^{\prime }}^t{\beta }_{\mathbf{2}})\prod _{r^{\prime }\in {\mathcal{D}}_{3l}}{\gamma }_{r^{\prime }}exp(x_{r^{\prime }}^t{\beta }_{\mathbf{3}}),\end{array}$$

where d_1j is the number of patients who experienced a non-terminal event in the interval (s_1,j−1, s_1,j], d_2k is the number of patients who experienced a terminal event but did not previously experience a non-terminal event in the interval (s_2,k−1, s_2,k], and d_3l = #{i : s_3,l−1 < Y_2i − Y_1i ≤ s_3,l, δ_1i = 1, δ_2i = 1} is the number of patients who have a time between effusion and death in interval (s_3,l−1, s_3,l]. ${\mathrm{\Delta }}_{ij}^g=max\{0,min(y_{1i},s_{g,j})-s_{g,j-1}\}$ for g = 1,2 and ${\mathrm{\Delta }}_{il}^3=max\{min(y_{2i}-y_{1i},s_{g,l})-s_{g,l-1}\}$. We denote by ℛ_gj the risk set ( the set of patients who have neither experienced event g nor been censored by time s_g,j−1) for interval I_g,j and let 𝒟_gj denote the set of patients who experienced event g in this interval. We follow Lee et al. and assign priors for g = 1, 2, 3

$$\begin{array}{c}{\lambda }_g\mid J_g,{\mu }_{{\lambda }_g},{\sigma }_{{\lambda }_g}^2~N_{J_g+1}({\mu }_{{\lambda }_g}\underset{\_}{1},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g}),\\ {\sigma }_{{\lambda }_g}^{-2}~\text{Gamma}(a_g,b_g),\\ \pi ({\mu }_{{\lambda }_g})\propto 1,\\ {\gamma }_i~\text{Gamma}({\theta }^{-1},{\theta }^{-1})\\ \text{and}\\ {\theta }^{-1}~\text{Gamma}(\psi ,\omega ).\end{array}$$

This prior formulation has hyperparameters a_g, b_g, ψ, and ω. Here Σ_λg is a function of the current partition s_g corresponding to a Multivariate Normal intrinsic conditional autoregression model (ICAR) as formulated by Besag and Kooperberg [12].

Lee et al. [9] consider the number of split points J_g to be a poisson random variable with mean α_g. They place a prior distribution on the partition s_g|J_g by drawing 2J_g + 1 uniform random variables on [0, s_g,max] and take the even indexed values as the split points. We also adopt this prior formulation, which limits the number of split point intervals that have no events.

2.2. Variable Selection Priors

Bayesian variable selection methods were introduced by George and McCulloch [13] [14] for normal linear models. The basic idea is to introduce a latent binary random vector η = (η₁, …, η_p) with η_k = 0 indicating that the variable x_(k) should be excluded from the model and η_k = 1 otherwise. Generalizing this notation to three hazard functions, we introduce three latent vectors η_g = (η_g,1, …, η_g,p) one for each hazard function g = 1, 2, 3, where η_g,k = 1 indicates that the variable x_(k) is important in hazard g and η_g,k = 0 otherwise. The indicator η_g,k is included in the prior distribution of β_g,k to define the mixture

$${\beta }_{g,k}\mid {\eta }_{g,k}~{\eta }_{g,k}N(0,{\tau }_{g,k}^2)+(1-{\eta }_{g,k}){\delta }_0({\beta }_{g,k}),$$ (4)

where δ₀(·) is the point mass distribution at 0. Mixture priors of type (4) are known as spike-and-slab priors in the Bayesian variable selection literature. Here we choose ${\tau }_{g,k}^2$ in (4) as the kth diagonal element of $c{\left(X_{({\eta }_g)}^t{X}_{({\eta }_g)}\right)}^{-1}$ with X_(ηg) denoting a matrix of the columns of X corresponding to η_g = 1, obtaining a prior resembling Zelner’s g-prior [15]. This prior mimicks the correlation structure of the data. Denote by β_(ηg) the coefficient vector corresponding to the entries of η_g = 1, and ${\beta }_{({\eta }_{\mathbf{g}}^{\mathbf{c}})}$ the coefficient vector corresponding to the entries of η_g = 0. Then the prior distribution of β_g|η_g can written as

$$\pi ({\beta }_{({\eta }_{\mathbf{g}})})~N\left[\underset{\_}{0},c{\left(X_{({\eta }_g)}^t{X}_{({\eta }_g)}\right)}^{-1}\right],$$ (5)

and that $P[{\beta }_{({\eta }_{\mathbf{g}}^{\mathbf{c}})}=\mathbf{0}]=1$. We assume η_g,k ~ Bernoulli(w_g) for all k = 1, …, p and g = 1, 2, 3. Formally, the prior of η_g|w_g is

$$\pi ({\eta }_{\mathbf{g}}\mid w_g)=\prod _{k=1}^p{w}_g^{{\eta }_{g,k}}{(1-w_g)}^{1-{\eta }_{g,k}}=w_g^{t_g}{(1-w_g)}^{p-t_g},$$

where $t_g={\sum }_{k=1}^p{\eta }_{g,k}$ is the number of η_g,k = 1 in hazard g. We assume a beta prior distribution for each of the w_gs with parameters z_g1 and z_g2. Following Brown et al. [16], we integrate out w_g to get the marginal prior for π(η_g) as

$$\pi ({\eta }_{\mathbf{g}})=\int \pi ({\eta }_{\mathbf{g}}\mid w_g)\pi (w_g)\mathrm{d}{w}_g=\frac{\mathit{Beta}(t_g+z_{g1},p-t_g+z_{g2})}{\mathit{Beta}(z_{g1},z_{g2})},$$

where Beta(·, ·) is the beta function.

2.3. Markov Chain Monte Carlo

For posterior inference, we implement a Markov Chain Monte Carlo (MCMC) sampling scheme with stochastic search variable selection (SVSS) applied on the three hazard functions that use add, delete and swap moves. We employ some of the same sampling schemes of Lee et al. but use different algorithms in our sampling of s_g, λ_g|s_g, μ_λg, σ_λg and the sequence of the Gibbs sampler. Lee et al. [9] used a random scan Gibbs sampler where the probability of adding an additional split point or deleting one of the current split points was a function the current number of split points and hyperparameters. The remaining moves are the frailty sampler, the hierarchical frailty parameter, 3 baseline hazards, 3 hierarchical baseline hazard parameters and 3 regression parameters, which are assigned equal probabilites from what is left after accounting for birth and death probabilities for the three different baseline hazard functions. Our approach differs in that we do not randomly select what move to perform at each iteration, and instead do all the moves for each of the three hazard functions consecutively. In summary, a generic iteration of the MCMC sampler does the following

• Update (η_g, β_g) jointly via a Metropolis step. This is done through add, delete, and swap moves. If t_g = 0, add one variable automatically and if t_g = p delete one variable automatically. Otherwise, with probability ϕ, perform a swap move. With probability 1−ϕ perform a Add/Delete move and randomly select one entry of η_g, say η_g,k, and if η_g,k = 1, perform a delete move, otherwise perform an add move. The details of these three moves are described below:

  1. Add If η_g,k = 0, set ${\eta }_{g,k}^{\ast }=1$ and sample β_g,k|β_g,(−k), η_g from a normal distribution. Denoting $\mathrm{\sum }=c{\left(X_{({\eta }_g^{\ast })}^t{X}_{({\eta }_g^{\ast })}\right)}^{-1}$, then the proposal distribution has mean ${\mu }_{\mathit{new}}={\mathrm{\sum }}_{k,(-k)}{\mathrm{\sum }}_{(-k),(-k)}^{-1}{\beta }_{({\eta }_g),(-k)}$ and a variance of ${\sigma }_{\mathit{new}}^2={\mathrm{\sum }}_{k,k}-{\mathrm{\sum }}_{k,(-k)}{\mathrm{\sum }}_{(-k),(-k)}^{-1}{\mathrm{\sum }}_{(-k),k}$. Denote Σ_k,k as the kth diagonal element of Σ, Σ_k,(−k) as the kth row without the kth column entry and Σ_{(−k),(−k)} as the submatrix without row and column k of Σ. The proposal (η_g^*, β_g^*) is accepted jointly with probability

     $$min\left[\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\beta }_{\mathbf{g}}}^{\ast },\dots )N({\beta }_{g,k}\mid {\mu }_{\mathit{new}},{\sigma }_{\mathit{new}}^2)\mathit{Beta}(t_g+1+z_{g,1},m_g-t_g-1+z_{g,2})}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{g}},\dots )\mathit{Beta}(t_g+z_{g,1},m_g-t_g+z_{g,2})},1\right].$$
  2. Delete If η_g,k = 1, set ${\eta }_{g,k}^{\ast }=0$ and ${\beta }_{g,k}^{\ast }=0$. Denote $R=c{\left(X_{({\eta }_g)}^t{X}_{({\eta }_g)}\right)}^{-1},{\mu }_{\mathit{old}}=R_{k,(-k)}{R}_{(-k),(-k)}^{-1}{\beta }_{({\eta }_g),(-k)}$ and variance ${\sigma }_{\mathit{old}}^2=R_{k,k}-R_{k,(-k)}{R}_{(-k),(-k)}^{-1}{R}_{(-k),k}$. Then the proposal ( ${\eta }_{\mathbf{g}}^{\ast },{\beta }_{\mathbf{g}}^{\ast }$) is accepted with probability

     $$min\left[\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\beta }_{\mathbf{g}}}^{\ast },\dots )\mathit{Beta}(t_g-1+z_{g,1},m_g-t_g+1+z_{g,2})}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{g}},\dots )N({\beta }_{g,k}\mid {\mu }_{\mathit{old}},{\sigma }_{\mathit{old}}^2)\mathit{Beta}(t_g+z_{g,1},m_g-t_g+z_{g,2})},1\right].$$
  3. Swap randomly select one η_g,k = 1 and one η_g,j = 0 and swap their values, setting ${\eta }_{g,k}^{\ast }=0$ and ${\eta }_{g,j}^{\ast }=1$. Then set ${\beta }_{g,j}^{\ast }=0$ and sample ${\beta }_{g,k}^{\ast }\mid {\eta }_{\mathbf{g}},{\beta }_{\mathbf{g},(-\mathbf{k})}$ from a normal distribution with mean μ_new and variance σ_new. These proposed values ( ${\eta }_{\mathbf{g}}^{\ast },{\beta }_{\mathbf{g}}^{\ast }$) are accepted with probability

     $$min\left[\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\beta }_{\mathbf{g}}}^{\ast },\dots )N({\beta }_{g,k}^{\ast }\mid {\mu }_{\mathit{new}},{\sigma }_{\mathit{new}}^2)}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{g}},\dots )N({\beta }_{g,j}\mid {\mu }_{\mathit{old}},{\sigma }_{\mathit{old}}^2)},1\right].$$

• Update β_(ηg) via a Metropolis step. β_(ηg) is first updated conditionally by sampling β_(ηg),k|η_g, β_(ηg),(−k) from a N(μ_old, σ_old) for all k = 1, …, p variables currently in hazard g. Then β_(ηg) is updated jointly by sampling a proposal ${\beta }_{({\eta }_{\mathbf{g}}^{\ast })}~N\left(\mathbf{0},c{\left(X_{({\eta }_g)}^t{X}_{({\eta }_g)}\right)}^{-1}\right)$. This provides better mixing in our Markov Chain by moving entries of β_(ηg) further from or closer to zero which affects future (β_g, η_g) updates.

• ε = θ⁻¹ via a Metropolis step in the same manner listed in the supplemental material of Lee et al.

• Update γ_i for i = 1, …, n via a Gibbs step in the same manner listed in the supplemental material of Lee et al.

• Update μ_λg and ${\sigma }_{{\lambda }_g}^2$ via a Gibbs step in the same manner listed in the supplemental material of Lee et al. for g = 1, 2, 3. The posteriors for each are normal and inverse-gamma distributed, respectively.

• Update λ_g,j|λ_g,(−j), s_g for j = 1, …, J_g + 1 via a Metropolis step. Lee et al. use the first and second derivatives of π(λ_g|Data) in the λ_g|s_g, μ_λg, ${\sigma }_{{\lambda }_g}^2$ proposal distribution. These derivatives involve β_g, which often has entries that change drastically in magnitude in the SVSS procedure, making the sampling scheme of Lee et al. extremely inefficient. Furthermore, the tuning parameter they use in the proposal distribution for λ_g must be tuned for each hazard g = 1, 2, 3 extensively to get good Metropolis-Hastings acceptance rates. To avoid these issues, we sampled ${\lambda }_{g,k}^{\ast }\mid {\lambda }_{g,(-k)}$ from a U (λ_g,k − c_g, λ_g,k + c_g) distribution where λ_g,k is the previous sampled value. This follows the approach of Haneuse et al. [17], and we use their default value c_g = .25 for each g, which gives good acceptance rates within our MCMC. Since the proposal ratio is $\frac{2c_g}{2c_g}=1$, the proposed value ${\lambda }_{g,k}^{\ast }$ is accepted with probability

  $$min\left[\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\lambda }_{\mathbf{g}}}^{\ast },\dots )N_{J_g+1}({{\lambda }_{\mathbf{g}}}^{\ast }\mid {\mu }_{{\lambda }_{\mathbf{g}}},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g})}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\lambda }_{\mathbf{g}},\dots )N_{J_g+1}({\lambda }_{\mathbf{g}}\mid {\mu }_{{\lambda }_{\mathbf{g}}},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g})},1\right].$$
• Add a split point to s_g and update (s_g, λ_g) jointly via a Metropolis-Hastings-Green step. Propose a new split point on $s_g^{\ast }~U[0,s_{g,\mathit{max}}]$ then the new ${\lambda }_g^{\ast }$ heights created by adding this split point are based on a multiplicative perturbation like in Green [18] and Lee et al. [9]. That is, if s^* is proposed such that it is in the interval [s_g,j−1, s_g,j ] then the new ${\lambda }_g^{\ast }$ values are

  $$\begin{array}{c}{\lambda }_{g,j}^{\ast }={\lambda }_{g,j}-\frac{s_{g,j}-s^{\ast }}{s_{g,j}-s_{g,j-1}}log\left(\frac{1-U_g}{U_g}\right)\\ \text{and}\\ {\lambda }_{g,j+1}^{\ast }={\lambda }_{g,j}+\frac{s_{g,j}-s^{\ast }}{s_{g,j}-s_{g,j-1}}log\left(\frac{1-U_g}{U_g}\right).\end{array}$$
  U_g ~ U[0, 1] is drawn at every iteration. This is the only difference in our sampler from the sampler of Lee et al. for the Metropolis-Hastings-Green step, as they set U_g as a tuning parameter. This move is accepted with probability

  $$min\left[\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\mathbf{s}}_{\mathbf{g}}}^{\ast },{{\lambda }_{\mathbf{g}}}^{\ast },\dots )P(J_g+1\mid {\alpha }_g)N_{J_g+1}({{\lambda }_{\mathbf{g}}}^{\ast }\mid {\mu }_{{\lambda }_{\mathbf{g}}},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g}^{\ast })(2J_g+3)(2J_g+2)(s_{g,\ast }-s_{g,j-1})(s_{g,j}-s_{g,\ast })}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\mathbf{s}}_{\mathbf{g}},{\lambda }_{\mathbf{g}},\dots )P(J_g\mid {\alpha }_g)N_{J_g+1}({\lambda }_{\mathbf{g}}\mid {\mu }_{{\lambda }_{\mathbf{g}}},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g})(s_{g,j}-s_{g,j-1})s_{g,\mathit{max}}^2{U}_g(1-U_g)},1\right].$$
• Delete a split point from s_g and update (s_g, λ_g) jointly via a Metropolis-Hastings-Green step. We randomly select one of the current split points that are not 0 or s_g,max with equal probability and delete it. Assume we delete split point s_g,j. Following the methods outlined by Green [18], we have that the multiplicative perturbation is $e^{{\lambda }_{g,j+1}-{\lambda }_{g,j}}=\frac{1-U_g}{U_g}$ and that the new height of the interval created by deleting a split point is a compromise of the previous two heights over this interval, defined as

  $${\lambda }_{g,j}^{\ast }=\frac{(s_{g,j}-s_{g,j-1}){\lambda }_{g,j}+(s_{g,j+1}-s_{g,j}){\lambda }_{g,j+1}}{s_{g,j+1}-s_{g,j-1}}.$$
  We draw a new U_g ~ U[0, 1] as in Green [18], rather than setting it to be a hyperparameter as in Lee et al. Now we accept the vector (s_g^*, λ_g^*) jointly with probability

  $$\begin{gathered} min \\ \left[\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\mathbf{s}}_{\mathbf{g}}}^{\ast },{{\lambda }_{\mathbf{g}}}^{\ast },\dots )P(J_g-1\mid {\alpha }_g)N_{J_g+1}({{\lambda }_{\mathbf{g}}}^{\ast }\mid {\mu }_{{\lambda }_{\mathbf{g}}},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g}^{\ast })(s_{g,j+1}-s_{g,j-1})s_{g,\mathit{max}}^2{U}_g(1-U_g)}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\mathbf{s}}_{\mathbf{g}},{\lambda }_{\mathbf{g}},\dots )P(J_g\mid {\alpha }_g)N_{J_g+1}({\lambda }_{\mathbf{g}}\mid {\mu }_{{\lambda }_{\mathbf{g}}},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g})(2J_g+1)(2J_g)(s_{g,j}-s_{g,j-1})(s_{g,j+1}-s_{g,j})},1\right]. \end{gathered}$$

2.4. Model Determination

To determine the final model on which to draw inference on our treatment and covariate effects on survival, we calculated the marginal posterior probabilities of inclusion for each variable k = 1, …, p in hazard function g as the proportion of η_g,k = 1 in the posterior sample. We then selected the variables in hazard g with marginal posterior probabilities of inclusion (PPI) greater than τ_g ∈ (0, 1). Formally, variable k = 1, …, p in hazard g = 1, 2, 3 was included in the final model if

$$P[{\eta }_{g,k}=1\mid \mathit{Data}]>{\tau }_g.$$ (6)

Thus, one must specify τ_g for each of the three hazard functions. We decided the optimum ${\tau }^{\ast }=({\tau }_1^{\ast },{\tau }_2^{\ast },{\tau }_3^{\ast })$ vector based on the deviance information via the DIC-τ_g procedure, defined as follows. Recall that the deviance information criterion of Spiegelhalter et al. [19] for β is

$$\mathit{DIC}=-2log(L(\widehat{\beta }))+2p_{\mathit{DIC}},$$ (7)

where $p_{\mathit{DIC}}=2\left(log(L(\widehat{\beta }))-\frac{1}{B}{\displaystyle \sum _{b=1}^B}log(L({\beta }^b)\right)$, β^b is the sampled value of β for iteration b and β̂ is the posterior mean of β = (β₁, β₂, β₃). Since our likelihood contains many nuisance parameters (γ, J_g, s_g, λ_g,…), Spiegelhalter et al. [19] reccommend to plug-in posterior means of these parameters in determining the DIC for a given β vector. We use the DIC to select the optimal model via the following algorithm, which we call the DIC-τ_g procedure.

1. Calculate the posterior mode or median of J_g for g = 1, 2, 3, depending on the shape of the posterior distribution. The posterior mode is calculated if the mode had a much greater posterior density than all other possible values for J_g while the posterior median of J_g is calculated if there were several values of J_g that occurred with about the same frequency.

2. Compute the posterior mean nuisance parameters γ = (γ₁, …, γ_n), s_g|J_g and λ_g|J_g for g = 1, 2, 3.

3. Perform a three-dimensional grid search for the optimum τ = (τ₁, τ₂, τ₃) over values τ_g = 0.05, 0.1, …, 0.9 that give different models based on the threshold criterion (6) for g = 1, 2, 3.

   1. For a given τ = (τ₁, τ₂, τ₃), find the ${\eta }^{\ast }=({\eta }_{\mathbf{1}}^{\ast },{\eta }_{\mathbf{2}}^{\ast },{\eta }_{\mathbf{3}}^{\ast })$ that satisfies (6).

   2. Sample ${\beta }_{({\eta }_{\mathbf{g}}^{\ast })}$ 10, 000 times via a Metropolis-Hastings algorithm using the prior distribution (5), the same c value used in the variable selection sampler and the posterior quantities calculated in steps 2 and 3.

   3. Discard the first half of the sample and save the DIC

4. The vector ${\tau }^{\ast }=({\tau }_1^{\ast },{\tau }_2^{\ast },{\tau }_3^{\ast })$ chosen by the DIC-τ_g procedure is the τ^* that produces the smallest DIC. For models with DIC values that differ by 1 or less from the model with the smallest DIC, the most parsimonious model was selected as the final model. A small decrease in DIC here indicates that including more variables does not increase the information criterion significantly over the more parsimonious model.

5. The final model includes the variables that satisfy (6) for the optimal ${\tau }^{\ast }=({\tau }_1^{\ast },{\tau }_2^{\ast },{\tau }_3^{\ast })$

After the DIC-τ_g procedure selects ${\eta }^{\ast }=({\eta }_{\mathbf{1}}^{\ast },{\eta }_{\mathbf{2}}^{\ast },{\eta }_{\mathbf{3}}^{\ast })$ based on ${\tau }^{\ast }=({\tau }_1^{\ast },{\tau }_2^{\ast },{\tau }_3^{\ast })$, we resample ${\beta }_{({\eta }_{\mathbf{g}}^{\ast })}$ 100, 000 times using the prior (5) ${\beta }_{({\eta }_{\mathbf{g}}^{\ast })}~N\left(\mathbf{0},c{\left(X_{({\eta }_g^{\ast })}^t{X}_{({\eta }_g^{\ast })}\right)}^{-1}\right)$ and do posterior inference after discarding the first 50, 000 MCMC samples. While we could compute the DIC for all 19³ different τ vectors, small changes in τ_g of .05 or .10 may not add any additional variables to hazard g, which means that two different τ_g vectors could lead to the same η_g. This reduces the number of τ_g values that we need to try based on our marginal posterior probabilities of inclusion. On the other hand, increasing τ_g by .05 could add more than one variable to hazard g. Since our case study has 11 variables, there are at most 11³ different τ = (τ₁, τ₂, τ₃) vectors that choose a unique subset of variables. We also did not consider a finer grid τ_g = .01, .02, … because using a spacing of .05 tends to include variables that occur with about the same frequency in the posterior distribution. This contrasts searching through the (2¹¹)³ total possible models without using the SVSS approach to find the lowest DIC. By performing the SVSS to obtain a posterior ordering of the variable importances, we compute the DIC for less than 0.0001% of the total possible models.

3. Simulation Study

We performed a simulation study under six different scenarios to see how well our method selected important variables in the posterior probabilities of inclusion, and how accurately the DIC-τ_g method selected the final model. We used the simID function from the SemiCompRisks package to simulate patient data under the Weibull semi-competing risks model, to examine how well our method performs when the baseline hazards are not truly piecewise exponential. For all simulation studies, we used κ₁ = .05, κ₂ = .01, κ₃ = .01, α₁ = .8, α₂ = 1.1, α₃ = .9 and θ = .5 which are the values given in the example for the simID documentation. Additionally, we set the censoring time for patients at 2000 days. For each simulated data set, we used the actual patient covariate matrix from our data to mimic a correlated data structure, rather than generating patient covariates independently. We performed the simulation study as follows for each simulation:

1. Run two MCMC chains using the package SCRSELECT [1] for 100,000 iterations with disperse starting values. One chain starts with all the variables included, the other starts with no variables included.

2. Discard the first 40,000 samples and combine the two chains, saving the marginal posterior probabilities of inclusion as well as the posterior means of nuissance parameters for the baseline hazard and frailties (s_g|J_g, λ_g|J_g, γ), as outlined in the DIC-τ_g procedure.

3. For τ_g = (.05, .1, …, .9) and g = 1, 2, 3 run an MCMC as described in section 2.4 for the DIC-τ_g procedure using the quantities from step 2 while skipping any (τ₁, τ₂, τ₃) vectors that do not change the variables included in each hazard

4. Find the combination τ₁, τ₂, τ₃ that produces the smallest DIC. When there are DIC values within 1 of each other for different models, take the one with less variables included (higher τ values).

5. Assess the results of the simulation.

We present results averaged over 100 replicated datasets for each scenario. For each of the seven scenarios we kept the last two entries of the β_g vectors constant and did not allow these to be selected from the model. These correspond to the propensity score and treatment effect of the XRT modality, respectively. These last two entries are set to (.15,−.15) for the hazard of effusion, (.3,−.2) for the hazard of death before effusion, and (.01,−.05) for the hazard of death after effusion. These values were selected in part to mimic the case study results. This allowed selection on 11 out of the 13 covariates in each hazard. Below is a summary of the six simulation scenarios that we considered for the DIC-τ_g method, where we only list the true coefficients of variables that were considered for variable selection.

Since gth hazard of the model includes e^X_tβ_g, entries of magnitude greater than 1 would be too unrealistic and easy to pick out in simulations. Instead we focused on coefficients having magnitudes of .3 to .9, with a few challenging coefficient values having magnitude less than .3. We used the same hyperparameter settings used in the application for the simulations for comparison. We set the variable selection hyperparameters c = 20 in (5) and (z_g1, z_g2) = (.4, 1.6) for g = 1, 2, 3. We set (a_g, b_g) = (ψ, ω) = (.7, .7) as a non-informitive prior for ${\sigma }_{{\lambda }_g}^{-2}$ and θ⁻¹. We set α_g = 3 corresponding to 3 expected split points in each baseline hazard, and the maximum possible number of split points to 10.

Before examining how well the DIC-τ_g procedure picked out the final model, we examined marginal posterior probability of inclusion results for the simulations in terms of included variables and excluded variables. In most hazards and senarios, the mean marginal probability of inclusion for the included variables is greater than .9. There are several exceptions to this that can be explained by the simulation settings. In scenario two hazard three, the mean marginal probability of inclusion for the two variables is .797, but the median is 1.00. This is due to the small true simulation value for variable 8 of .2, which is much harder to detect in the SVSS.

In Table 2, we display a summary of the results of the DIC-τ_g procedure showing the mean number of false positives, false negatives, and the mean probability of a correct decision. We denote NFP= mean number of false positives and N₀ = total number of variables with true β_g,k = 0 for all three hazards combined. Similarly, NFN= mean number of false negatives and N₊ = total number of variables with true β_g,k ≠ 0 for all three hazards combined. We denote PCD as the probability of a correct decision of whether or not a variable is included. We also computed a statistic resembling the area under the curve (AUC) where we plotted the true positive and false positive rates of all 100 simulations, connected these points in the same manner as the ROC curve and estimated the area under this curve. This statistic, which we denote AUC* operates in the same manner as the traditional AUC statistic where larger values indicate a better classifier and values near .5 indicate a poor classification method. We used this since it evaluated the DIC-τ_g procedure rather than just the SVSS portion like the traditional AUC score would. The AUC* and AUC statistics were undefined and omitted for scenario 7 since there were no true positives.

Table 2.

Simulation Study of the DIC-τ_g Procedure.

Scenario #	NFP/N0	NFN/N+	PCD	AUC*
1	5.92/20	0.48/13	0.806	0.972
2	7.29/23	0.50/10	0.764	0.957
3	5.94/28	0.00/5	0.820	1.000
4	5.75/21	0.28/12	0.817	0.935
5	6.21/24	0.45/9	0.798	0.928
6	5.66/13	1.98/20	0.769	0.881
7	5.88/33	0.00/0	0.822	——

In all seven scenarios the DIC-τ_g method correctly determined variable inclusion on average with probability .76 to .82 and the AUC* scores for the simulations were all greater than .88, showing that the DIC-τ_g procedure performs well in determining variable inclusion. The DIC-τ_g method correctly identified the true model in at least one simulation for scenarios 2,3 and 7. The majority of the incorrect decisions about variable inclusion were false positives, and false negatives did not even occur in scenarios 3 or 7 which are the sparse and null scenarios. Each scenario had about 6 false positives on average, with the second scenario having the highest mean false positive rate. The false positives are partially due to correlations among the covariates, and not imposing enough separation in the marginal posterior probabilities of inclusion, which can be mitigated through careful adjustments to the hyperparameter c.

4. Application

4.1. Data

This observational data set came from M.D. Anderson Cancer Center in Houston, TX. It consists of 470 esophageal cancer patients who had one of two XRT modalities for radiation: 3-Dimensional Conformal Radiation Therapy (3D-CRT) or Intensity Modulated Radiation Therapy (IMRT). Some patients also received induction chemotherapy. Patients were followed from the end of radiation therapy until death or censoring. The dates pleural or pericardial effusion occured were recorded during this time. The two path diagrams in Figure 1 describe the semi-competing risks structure and enumerate the different patient outcomes. In each of these paths, we display the total number of patients who experienced each event followed by the numbers of patients who received 3D-CRT and IMRT, respectively, in each transition. Pleural effusion occurs much more frequently in these patients than pericardial effusion. Patients who experienced either Pericardial or Pleural effusion died afterwards in over 75% of all cases (no censoring).

Figure 1.

Path diagrams for the three event types along with how many patients (Total, 3D-CRT, IMRT) experienced each for pleural and pericardal effusion. 212 patients received 3D-CRT and 258 patients recieved IMRT.

We did separate analyses for the pleural effusion and pericardial effusion path structures shown in Figure 1. Each patient had 20 baseline covariates, including individual characteristics and characteristics related to their tumor. Several patient covariates had high pairwise correlations or a small number of patients. Because this caused severe MCMC convergence problems, these variables were excluded from the analysis. The covariates considered were XRT modality, induction chemotherapy, age, BMI, asthma, diabetes, smoking status, and also binary variables for whether or not a patient had an adeno histology, a good KPS performence score, stage 3–4 cancer, and for tumor location 3 (lower/distal) or tumor location 2 (middle) vs tumor location 1 (upper). Because patients did not have smoking status, BMI, or tumor histology information, they were removed from the data, leaving 470 patients. Clinicians were primarily interested in comparing the effects of the two modalities on pleural effusion, pericardial effusion, and death, but it was unclear what covariates should be included in each hazard function. We addressed this concern through our variable selection method for the three hazard functions. We included IMRT status in each hazard to evaluate radiation therapy modality effects on each of the three hazard functions. Because the data were observational and not randomized, we included the propensity score of each patient as a covariate always in each hazard to correct for some of the bias introduced. The propensity score was estimated by logit⁻¹(Pr(IMRT|X)) = .25 + .48(Hypertension) − .20(Differentation) + .30(Adeno Histology), the fitted logistic regression model of these covariates on IMRT status. We did not allow the propensity score or IMRT status to be removed from the model. Thus, X_(ηg) always contains a column with individual propensity scores and XRT status. Likewise, β_(ηg) always contains an entry corresponding to the estimated coefficient for the propensity score and XRT status in each hazard function.

4.2. Hyperparameter Settings

For the hyperparameters, we set c = 20 in (5) for both case studies. We found that varying c greatly changed the posterior inclusion probabilities, with larger values of c forcing more variables out of the model and smaller values keeping more variables in the model. Smith and Kohn [20] reccomend a value between 10 and 100. We obtained vague priors on w_g as in Brown et al. [16] by imposing the constraint z_g1 + z_g2 = 2, corresponding to a prior effective sample size of 2 for the beta prior of the covariate inclusion probability, with some desirable mean percentage of inclusion. We set (z_g1, z_g2) = (.4, 1.6) for g = 1, 2, 3, corresponding to an expectation of 2 to 3 variables being included in each hazard function. We set (a_g, b_g) = (ψ, ω) = (.7, .7) as a non-informitive prior for ${\sigma }_{{\lambda }_g}^{-2}$ and θ⁻¹. This corresponds to .025 and .975 quantiles of .23 and 155.61 for ${\sigma }_{{\lambda }_g}^2$ and θ. We set α_g = 3 corresponding to 3 expected split points in each baseline hazard, and the maximum possible number of split points to 10, which neither data set reached for any hazard. Hyperparameter settings for the ICAR formulation are discussed in the appendix. For both data sets, two chains were run with two different starting values for the three hazard β_g vectors; the first with all η_g,k = 1 and β_g,k = 1 for all k = 1, .., p and g = 1, 2, 3 the second with η_1,3 = 1,η_2,5 = 1 and η_3,7 = 1 (these entries were randomly chosen) and all non-zero coefficients set to β_g,k = −1.

4.3. Case Study Results: Pleural Effusion

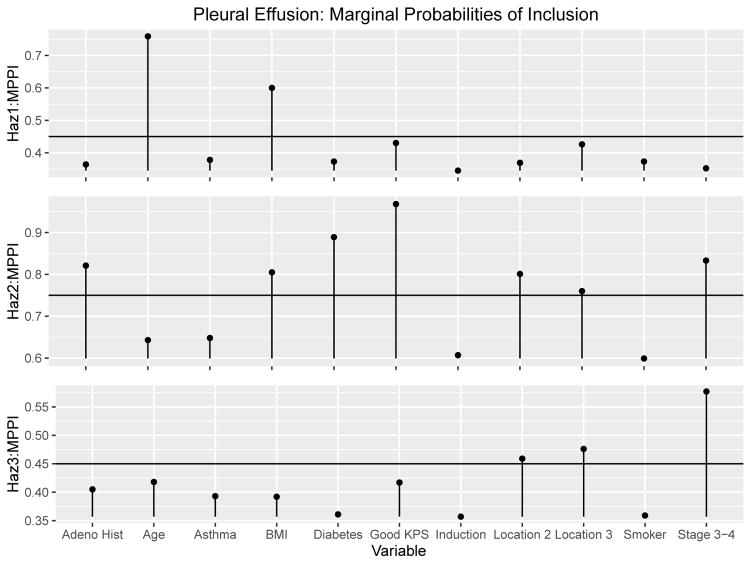
The two chains were run for 100, 000 iterations with the first 40, 000 discarded as burn-in. The scale reduction factors for the β_g coefficients had estimates and upper confidence interval estimates below 1.01, which indicates good convergence for both chains along with the trace plots for each [21]. Furthermore, the posterior probabilities of inclusion for the two chains did not differ substantially, with the biggest difference of 4.46%. The correlation of the marginal posterior probabilities of inclusion for the two chains were all above .99 for all three hazards. The posterior samples of both chains were then combined and the resulting marginal posterior probabilities of inclusion can be seen graphically in Figure 2 and numerically in Table 5.

Figure 2.

Pleural Effusion Results: Combined Marginal Posterior Probabilities of inclusion and the DIG-τ_g cutoff threshholds ${\tau }_g^{\ast }$

Table 5.

Sensitivity Analysis of prior hyperparameter effects on marginal PPI for the Pleural Effusion case study. Notation: c is a parameter in the prior of β_(ηg), given in (5) and (z_g1, z_g2) are the prior hyperparameters on w_g, the probability that η_g,k = 1, given on page 4.

Variable (zg1, zg2) =	c = 20 (.4, 1.6)	c = 30 (.4, 1.6)	c = 20 (.1, 1.9)	c = 30 (.1, 1.9)
	h1: Effusion before Death
Asthma	.378	.184	.207	.080
Diabetes	.373	.174	.199	.073
Stage 3–4	.352	.168	.191	.071
Location 2	.369	.174	.201	.077
Location 3	.426	.209	.227	.091
Age	.759	.629	.509	.361
Smoker	.373	.181	.194	.074
BMI	.600	.378	.343	.165
Induction Chemo	.345	.166	.191	.071
Good KPS	.430	.253	.242	.111
Adeno Histology	.364	.176	.197	.071
	h2: Death w/o Effusion
Asthma	.648	.451	.513	.291
Diabetes	.889	.760	.779	.543
Stage 3–4	.833	.712	.731	.507
Location 2	.801	.631	.686	.421
Location 3	.760	.583	.638	.400
Age	.643	.479	.562	.330
Smoker	.599	.412	.500	.272
BMI	.805	.621	.667	.400
Induction Chemo	.607	.419	.497	.270
Good KPS	.968	.922	.896	.713
Adeno Histology	.821	.623	.717	.466
	h3: Death after Effusion
Asthma	.393	.273	.296	.169
Diabetes	.361	.223	.251	.136
Stage 3–4	.577	.451	.443	.292
Location 2	.459	.321	.345	.195
Location 3	.476	.325	.347	.189
Age	.418	.293	.317	.186
Smoker	.359	.238	.261	.146
BMI	.392	.254	.277	.149
Induction Chemo	.357	.225	.263	.134
Good KPS	.417	.283	.301	.168
Adeno Histology	.405	.264	.291	.151

The optimal model based on the DIC-τ_g had a DIC of 1050.845 and indicated that $({\tau }_1^{\ast },{\tau }_2^{\ast },{\tau }_3^{\ast })=(.45,.75,.45)$ was the appropriate vector of upper bounds to produce the optimum model. This model had 2, 7 and 3 variables in hazards 1, 2 and 3, respectively. After finding the optimal model, the Gibbs sampler was rerun using 100, 000 iterations. Table 3 displays the fitted optimal model with 95% posterior credible intervals for the hazard ratio exp[β_g,k] and P = P[β_g,k > 0|Data] for the kth variable included in each hazard. That is, P is the posterior probability that the effect of covariate k increases the hazard of event g, so that large values of P, above .95 or .99, correspond to a harmful effect of the covariate.

Table 3.

Pleural Effusion Case Study: Posterior quantities for the model chosen by DIC-τ_g procedure. Notation: P = P[β_g,k > 0|Data], HR (CI) = posterior hazard ratio and 95% credible interval. g = 1, 2, 3 correspond to the three hazard functions and k = 1, …, p index to the covariates.

Variable	h1: Effusion		h2: Death w/o Effusion		h3: Death after Effusion
	HR (CI)	P	HR (CI)	P	HR (CI)	P
Asthma	—	—	—	—	—	—
Diabetes	—	—	1.18 (1.03–1.33)	.99	—	—
Stage 3–4	—	—	1.13 (1.00–1.29)	.97	1.19 (1.03–1.37)	.99
Location 2	—	—	.86 (.74–1.01)	.03	1.18 (.98–1.41)	.96
Location 3	—	—	.87 (.73–1.04)	.06	1.18 (.99–1.42)	.97
Age	1.18 (1.04–1.36)	.99	—	—	—	—
Smoker	—	—	—	—	—	—
BMI	.90 (.78–1.02)	.05	.88 (.76–1.00)	.03	—	—
Induction Chemo	—	—	—	—	—	—
Good KPS	—	—	.80 (.71–.91)	< .01	—	—
Adeno Histology	—	—	1.21 (1.02–1.42)	.99	—	—
Propensity Score	.97 (.86–1.12)	.34	.92 (.81–1.05)	.10	.98 (.88–1.11)	.40
IMRT	.84 (.74–.96)	< .01	.85 (.75–.97)	< .01	.98 (.85–1.13)	.40

We see from the final model chosen by the DIC-τ_g procedure that patients with IMRT radiation had significantly reduced hazards of pleural effusion and death before pleural effusion compared to 3D-CRT (P < .01). Older age greatly increased the hazard of pleural effusion (P = .99) and patients with Stage 3–4 cancer had an increased hazard of death after pleural effusion (P = .99). Patients with diabetes and adeno histology had significantly increased hazards of death before pleural effusion (P = .99) and patients with a good KPS score had a significantly reduced hazard of death before pleural effusion P <.01. Stage 3–4 cancer increased the hazard of death before pleural effusion (P = .97) but patients with stage 3–4 cancer had a significantly increased risk of death before pericardial effusion (Table 4). This could be attributed to the number of patients who died without pericardial effusion (n = 285) compared to those who died without pleural effusion (n = 197).

Table 4.

Pericardial Effusion Case Study: Posterior quantities for the model chosen by DIC-τ_g procedure. Notation: P = P[β_g,k > 0|Data], HR (CI) = posterior hazard ratio and 95% credible interval. g = 1, 2, 3 correspond to the three hazard functions and k = 1, …, p index to the covariates.

Variable	h1: Effusion		h2: Death w/o Effusion		h3: Death after Effusion
	HR (CI)	P	HR (CI)	P	HR (CI)	P
Asthma	—	—	—	—	—	—
Diabetes	.91 (.75–1.09)	.15	1.14 (1.03–1.27)	> .99	1.11 (.90–1.36)	.83
Stage 3–4	—	—	1.30 (1.17–1.45)	> .99	—	—
Location 2	1.16 (.95–1.42)	.93	—	—	—	—
Location 3	1.20 (.94–1.54)	.92	—	—	1.10 (.92–1.33)	.85
Age	.85 (.72–1.06)	.03	—	—	—	—
Smoker	.89 (.74–.106)	.09	—	—	—	—
BMI	.91 (.76–1.09)	.16	.85 (.76–.95)	< .01	—	—
Induction Chemo	—	—	—	—	—	—
Good KPS	—	—	.83 (.75–.92)	< .01	—	—
Adeno Histology	.83 (.68–1.03)	.04	1.21 (1.08–1.37)	> .99	—	—
Propensity Score	1.07 (.89–1.30)	.75	.96 (.87–1.08)	.25	1.00 (.87–1.17)	.51
IMRT	.73 (.62–.87)	< .01	.80 (.72–.89)	< .01	1.08 (.90–1.30)	.81

4.4. Case Study Results: Pericardal Effusion

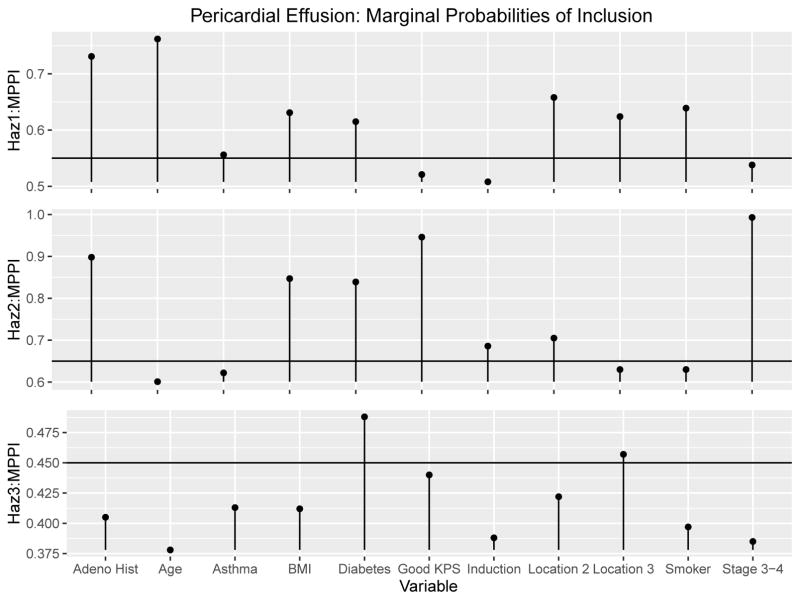
The two chains were run for 100, 000 iterations with the first 40, 000 discarded as burn-in. The scale reduction factors for the β_g coefficients had estimates and upper confidence interval estimates below 1.01, which indicates good convergence for both chains along with the trace plots for each [21]. The posterior probabilities of inclusion for the two chains did not differ substantially, with the biggest difference 2.80%. The correlation of the marginal posterior probabilities of inclusion for the two chains were .994, .995 and .972 for the three hazards, respectively. The posterior samples of both chains were combined and the resulting marginal posterior probabilities of inclusion can be seen graphically in Figure 3 and numerically in Table 7.

Figure 3.

Pericardial Effusion Results: Combined Marginal Posterior Probabilities of inclusion and the DIG-τ_g cutoff threshholds ${\tau }_g^{\ast }$

Table 7.

Sensitivity Analysis of prior hyperparameter effects on marginal PPI for the Pericardial Effusion case study. Notation: c is a parameter in the prior of β_(ηg), given in (5) and (z_g1, z_g2) are the prior hyperparameters on w_g, the probability that η_g,k = 1, given on page 4.

Variable	c = 20	c = 30	c = 20	c = 30
(zg1, zg2) =	(.4, 1.6)	(.4, 1.6)	(.1, 1.9)	(.1, 1.9)
	h1: Effusion before Death
Asthma	.556	.277	.338	.130
Diabetes	.615	.399	.418	.192
Stage 3-4	.538	.305	.357	.137
Location 2	.658	.410	.439	.199
Location 3	.624	.363	.410	.167
Age	.762	.551	.525	.276
Smoker	.639	.394	.435	.191
BMI	.631	.412	.436	.199
Induction Chemo	.508	.388	.329	.126
Good KPS	.521	.440	.347	.130
Adeno Histology	.731	.405	.508	.257
	h2: Death w/o Effusion
Asthma	.622	.460	.568	.400
Diabetes	.839	.745	.820	.703
Stage 3-4	.993	.993	.990	.975
Location 2	.705	.562	.688	.538
Location 3	.630	.485	.579	.425
Age	.601	.462	.565	.413
Smoker	.630	.479	.577	.423
BMI	.847	.759	.831	.673
Induction Chemo	.686	.563	.638	.490
Good KPS	.946	.923	.929	.880
Adeno Histology	.898	.839	.867	.789
	h3: Death after Effusion
Asthma	.413	.242	.222	.122
Diabetes	.488	.315	.271	.172
Stage 3-4	.385	.216	.204	.110
Location 2	.422	.259	.227	.135
Location 3	.457	.282	.251	.142
Age	.378	.215	.206	.109
Smoker	.397	.231	.218	.116
BMI	.412	.236	.218	.119
Induction Chemo	.388	.225	.212	.111
Good KPS	.440	.270	.244	.134
Adeno Histology	.405	.237	.218	.119

Variables above the thresholds in Figure 3 are included in the final model. The optimal model based on the DIC-τ_g procedure had a DIC of 895.37, with τ^* = (.55, .65, .45). This model produced 7, 6, and 2 variables in hazards 1, 2, and 3, respectively. After finding the optimal model, the Gibbs sampler was rerun using 100, 000 iterations and the first 50, 000 samples were discarded as burn-in. Table 4 displays the fitted optimal model with 95% posterior credible intervals for the hazard ratio exp[β_g,k] and P = P[β_g,k > 0|Data], the posterior probability that a larger value of a covariate is more hazardous, for the kth variable included in each hazard g. We used the same hyperparameter settings for this model as for the pleural effusion model, namely c = 20, z_g1 = .4 and z_g2 = 1.6.

Table 4 shows that patients with IMRT had significantly decreased hazards of pericardial effusion and death before pericardial effusion, compared to those who received 3D-CRT (P < .01 for both hazards). All other 95% credible intervals for the hazard of pericardial effusion contain 1, so even though Age and Adeno histology had coefficients that indicated the hazard decreased with these variables (P = .03 and .04) they only decreased the hazard of pericardial effusion slightly. The final model for the hazard of death before pericardial effusion has clearer trends, namely patients with Stage 3–4 cancer, Diabetes, or an Adeno Histology had significantly increased hazards of death without prior pericardial effusion (P > .99), evidenced by the 95 % credible intervals. IMRT was associated with a significant reduction in the hazard of death prior to pericardial effusion as did patients with an increased BMI (P < .01). No variables included in the hazard of death after pericardial effusion changed the hazard significantly, indicating that patient baseline covariates and radiation therapy have little effect on survival following pericardial effusion.

4.5. Sensitivity Analyses

We assessed how sensitive the marginal posterior probabilities of inclusion and model selected via the DIC-τ_g procedure were to the hyperparameters c, z_g1 and z_g2. Because we wanted to distinguish among variables, we did not consider c and (z_g1, z_g2) values that force all variables in or out of the model. For c, first we found a range of appropriate values for the data that did not include or exclude all the variables. Varying c within this range of appropriate values did not have a large impact on the final models. We tested sensitivity of our model to c by looking at c = 20 and c = 30, in conjunction with two w_g hyperparameter combinations of (z_g1, z_g2) = (.4, 1.6) as in the primary analysis and (z_g1, z_g2) = (.1, 1.9) corresponding to an expectation of 1 or 2 variables included in each hazard. We found that our method was sensitive to the choices of c and (z_g1, z_g2) in shrinking the marginal posterior probabilities of inclusion, but that the final model chosen by the DIC−τ_g procedure did not differ much. This helps address concerns about the sensitivity of the model to final inferences based on treatments and covariates. For sensitivity to the survival hyperparameters, we refer to the supplemental material of Lee et al. [9].

To assess sensitivity to the pleural effusion case study, Table 5 shows the marginal posterior probability of inclusion in each hazard function for each of the four different settings of c and z_g1. For each hazard function, increasing c had a greater shrinkage impact than decreasing z_g1 for the pleural effusion data.

In general, the ordering of importance of the variables by marginal Posterior Probablies of Inclusion (PPIs) does not change much. The primary difference in ordering comes for variables that have lower marginal PPIs relative to the variables with the highest PPIs in each hazard, because these variables tend to have marginal PPIs very close to each other, which increases the likelihood of different orderings by chance alone. As mentioned previously, different values of c and z_g1 induce different degrees of sparsity, so we wanted to know if our final model selected via the DIC-τ_g procedure was sensitive to c and z_g1. Table 6 displays the final models selected by the DIC-τ_g procedure for each of the four models considered. The same two variables, Age and BMI, were chosen in the final model for all but one hyperparameter setting. In all four settings, the hazard of pleural effusion was decreased significantly for patients who had IMRT radiation (P <.01) and increased for patients with older age (P ≥ .99). For the hazard of death before pleural effusion, the variables Diabetes, Stage 3-4, Location 2, Location 3, BMI, good KPS and adeno Histology were included for all four hyperparameter settings. In all four settings, the hazard of death before pleural effusion was reduced significantly for patients with IMRT radiation (P ≤ .01). All four hyperparameter settings had Stage 3-4 in the final model for the hazard of death after pleural effusion, and in each model, having stage 3-4 cancer significantly increased a patient’s hazard of death after pleural effusion (P ≥ .99). In models including more than just Stage 3-4 cancer in h₃, all other credible intervals contained 1, indicating that Stage 3-4 cancer is the key driver for this hazard.

Table 6.

Sensitivity Analysis of prior hyperparameter effects on the model selected in the Pleural Effusion case study. Notation: c is a dispersion parameter in the prior of β_(ηg), given in (5) and (z_g1, z_g2) are the beta prior hyperparameters on w_g, the probability that η_g,k = 1 for k = 1, ..., p, given on page 4.

c	(zga, zgb)	Included Variables
		h1: Effusion before Death
20	(.4, 1.6)	Age, BMI
30	(.4, 1.6)	Age, BMI
20	(.1, 1.9)	Age, BMI
30	(.1, 1.9)	Age
		h2: Death w/o Effusion
20	(.4, 1.6)	Diabetes, Stage 3-4, Location 2, Location 3, BMI, Good KPS, Adeno Histology
30	(.4, 1.6)	Diabetes, Stage 3-4, Location 2, Location 3, BMI, Good KPS, Adeno Histology
20	(.1, 1.9)	Diabetes, Stage 3-4, Location 2, Location 3, BMI, Good KPS, Adeno Histology
30	(.1, 1.9)	Diabetes, Stage 3-4, Location 2, Location 3, BMI, Good KPS, Adeno Histology
		h3: Death after Effusion
20	(.4, 1.6)	Stage 3-4, Location 2, Location 3
30	(.4, 1.6)	Stage 3-4, Location 2, Location 3
20	(.1, 1.9)	Stage 3-4, Location 2, Location 3, Age, Good KPS
30	(.1, 1.9)	Stage 3-4

Next, we similarly assessed the sensitivity of the pericardial effusion data set to the variable selection hyperparameters. For the first two hazard functions, increasing c caused more shrinkage than decreasing z_g1 while the third hazard function achieved more shrinkage by lowering z_g1. The four different settings considered had good agreement for the order of importance based on marginal posterior probability of inclusion for the second and third hazard functions. Table 7 shows that Stage 3-4, good KPS and Adeno histology had the three highest marginal posterior probabilities of inclusion (in order) for the hazard of death before pericardial effusion in all four settings considered. Diabetes, Location 3 and a good KPS score had the highest three marginal posterior probabilities of inclusion for the hazard of death after pericardial effusion for all four models considered. There was, however, more sensitivity to c and z_g1 for the hazard of pericardial effusion. While all four settings identified Age as the variable with highest marginal posterior probability of inclusion for hazard 1, three out of the four models identified Adeno Histology and Location 3 and the second and third most important variables based on the marginal PPI. The model that didn’t identify this trend, with c = 30 and (z_g1, z_g2) = (.4, 1.6), had four variables with marginal PPI values between .40 and .44, which included the variables associated with Adeno Histology and a good KPS score. This discrepancy in ordering could be due, in part, to these four marginal PPI values being close to each other. In Table 8, we see the final models selected by the DIC-τ_g procedure for each of the four models considered.

Table 8.

Sensitivity Analysis of prior hyperparameter effects on the model selected in the Pericardial Effusion case study. Notation: c is a dispersion parameter in the prior of β_(ηg), given in (5) and (z_g1, z_g2) are the beta prior hyperparameters on w_g, the probability that η_g,k = 1 for k = 1, ..., p, given on page 4.

c	(zga, zgb)	Included Variables
		h1: Effusion before Death
20	(.4, 1.6)	Diabetes, Location 2, Location 3, Age, Smoking Status, BMI, Adeno Histology
30	(.4, 1.6)	Diabetes, Location 2, Location 3, Age, Smoking Status, BMI, Adeno Histology
20	(.1, 1.9)	Diabetes, Location 2, Location 3, Age, Smoking Status, BMI, Adeno Histology
30	(.1, 1.9)	Diabetes, Location 2, Location 3, Age, Smoking Status, BMI, Adeno Histology
		h2: Death w/o Effusion
20	(.4, 1.6)	Diabetes, Stage 3-4, BMI, Good KPS, Adeno Histology
30	(.4, 1.6)	Diabetes, Stage 3-4, BMI, Good KPS, Adeno Histology
20	(.1, 1.9)	Diabetes, Stage 3-4, BMI, Good KPS, Adeno Histology
30	(.1, 1.9)	Diabetes, Stage 3-4, BMI, Good KPS, Adeno Histology
		h3: Death after Effusion
20	(.4, 1.6)	Diabetes, Location 3
30	(.4, 1.6)	Diabetes
20	(.1, 1.9)	Diabetes, Location 3
30	(.1, 1.9)	Diabetes

The models chosen for the pericardial effusion data do not differ much for the four c and z_g1 values considered. The hazard of pericardial effusion included Diabetes, Location 2, Location 3, Age, Smoking Status, BMI and Adeno histology in all four models considered. All four models included Diabetes, Stage 3-4, BMI, a good KPS score and Adeno Histology in the hazard of death before pericardial effusion. The variables selected for the hazard of death after pericardial effusion showed some sensitivity to c and z_g1 choices, but all four models contained Diabetes as a covariate. Additionally, the conclusion that no covariates impact the hazard of death after pericardial effusion did not change for any of the four models.

5. Discussion

We have developed a variable selection procedure for a three-hazard model for semi-competing risks data using spike-andslab priors and the Stochastic Variable Selection Search (SVSS) algorithm. We devised a criterion, DIC-τ_g, for choosing the threshold on the marginal posterior probability of variable inclusion based on the Deviance Information Criteria. As seen in the sensitivity analyses, the DIC-τ_g procedure led to similar selected models, regardless of the choices of the hyperparameters c, z_g1 and z_g2. The hazard of death before effusion of either type chose the same set of variables for all hyperparameter choices in both data sets. The hazard of pericardial effusion had the same set of variables for all four settings and the remaining hazard functions had minor differences in variables chosen. Clearly, there is a substantial effect of c and (z_g1, z_g2) on decisions about variable inclusion in the final model when choosing an arbitrary τ_g. The DIC-τ_g procedure mitigates much of this sensitivity.

Our simulation study showed that the DIC-τ_g procedure performs well in determining which variables should be included in the model. This method can display a substantial improvement by tuning the sparsity parameter c to separate the marginal posterior probabilities of inclusion of the variables.

In an application to data from esophageal cancer patients, we were able to use this procedure to select the important covariates in each of the three hazards and use the final variables included to evaluate the treatment and covariate effects on the hazards of effusion, death before effusion, and death after effusion. In our selected models, we saw the same medical conclusion, there was strong evidence that patients with IMRT radiation had significantly reduced risks of pericardial effusion, pleural effusion, and death before either effusion type. Further evidence of this treatment effect was shown in the SVSS posteriors with P[β_1,IMRT > 0|Data] = .02 and P[β_2,IMRT > 0|Data] = .04 for pleural effusion and P[β_1,IMRT > 0|Data] < .01 and P[β_2,IMRT > 0|Data] < .01 for pericardial effusion. For the models determined by the SVSS algorithm, patients who received IMRT had significantly reduced risks of pericardial and pleural effusion as well as death before effusion type. This agrees with results from several previous studies which showed that IMRT increased patient survival compared to 3D-CRT [22] [23].

The proposed method provides a flexible, practical variable selection procedure for semi-competing risks. The SVSS algorithm for semi-competing risks is implemented in the package SCRSELECT [1], which is now available on CRAN. This function computes and saves all posterior quantities and returns the marginal posterior probabilities of inclusion for each hazard function. The code allows for 0, 1, .., p − 2 variables to be excluded from the selection procedure, while we kept two variables out of the selection procedure to evaluate the treatment effect in our application. This program takes between two and four hours to run 100,000 iterations, depending on the number of split points in each hazard during the MCMC. Additionally, there is a program that runs the SVSS algorithm on two disperse chains followed by the DIC-τ_g procedure which performs a grid search through all the possible models for given vectors of marginal posterior probabilities of inclusion. This takes six to twelve hours depending on the separation of the variables in terms of marginal posterior probabilities of inclusion and returns these posterior probabilities, the threshold of inclusion and the final model selected by the DIC-τ_g procedure.

Table 1.

Simulation Scenarios.

Hazard Component Scenario #	β1 h1: Non-Terminal Event	β2 h2: Death w/o Non-Terminal Event	β3 h3: Death after Non-Terminal Event
1	(.9,0,−.7,0,0,0,0,−.6,0,0,.5)	(−.5,0,0,.7,0,0,0,.7,−.7,.5,0)	(.6,0,0,−.5,0,−.6,0,−.8,0,0,0)
2	(.9,0,−.7,0,0,0,0,−.6,0,0,.5)	(.7,0,0,−.2,0,0,0,.3,0,−.45,0)	(−.9,0,0,0,0,0,0,.2,0,0,0)
3	(0,0,0,0,.9,0,0,0,0,−.7,0)	(0,0,0,0,0,0,0,0,0,0,−.6)	(.6,−.7,0,0,0,0,0,0,0,0,0)
4	(0,−.7,.6,0,0,0,.3,.5,0,−.9,.4)	(−.85,0,0,−.4,0,0,0,.3,0,.8,0)	(−.5,0,0,0,0,0,0,.6,0,0,0)
5	(−.7,0,0,−.5,0,.9,0,0,0,0,0)	(.4,0,0,−.6,0,0,0,0,−.7,0,.5)	(−.3,0,0,.8,0,0,0,0,0,0,0)
6	(.8,.7,.4,−.7,−.7,−.8,0,0,0,0)	(.8,−.7,.9,0,0,0,0,0,.8,−.4,−7)	(.4,.8,−.7,.35,.8,−.9,.4,−.7,0,0,0)
7	(0,0,0,0,0,0,0,0,0,0,0)	(0,0,0,0,0,0,0,0,0,0,0)	(0,0,0,0,0,0,0,0,0,0,0)

Appendix: MCMC algorithm details on (η_g, β_g) and λ_g updates

We report additional details of the (η_g, β_g) and λ_g Markov Chain Monte Carlo samplers here.

• Update (η_g, β_g) update via a Metropolis step. With probability ϕ we randomly choose one entry of η_g and if it is 0, set it to 1, while if it is 1, set it to 0. With probability 1 − ϕ, we randomly choose one entry that is a 1 and a random entry that is 0 and change their values. If for some reason there are no values of 1 or 0 in the previous iteration, we can only perform an add or delete step and randomly choose one entry to change. We then update β_g in the following way under 3 different scenarios. If η_g,k is “deleted”, we set β_g,k = 0 and ${\eta }_{g,k}^{\ast }=0$. If η_g,k is ”added”, we sample ${\beta }_{g,k}^{\ast }$ from ${\beta }_{g,k}\mid {\eta }_g^{\ast }$, β_g,(−k) and set ${\eta }_{g,k}^{\ast }=1$. Finally if η_g,k = 0 and η_g,j = 1 are swapped then we set ${\eta }_{g,j}^{\ast }=0,{\eta }_{g,k}^{\ast }=1,{\beta }_{g,j}^{\ast }=0$ and we sample ${\beta }_{g,k}^{\ast }$ from the distribution of ${\beta }_{g,k}\mid {\eta }_g^{\ast }$, β_g,(−k). The vectors ${\eta }_{\mathbf{g}}^{\ast }$ and ${\beta }_{\mathbf{g}}^{\ast }$ are jointly accepted over the previous values (η_g, β_g) with probability ${\alpha }_1^{\ast },{\alpha }_2^{\ast },{\alpha }_3^{\ast }=min({\alpha }_1,1)$, min(α₂, 1), min(α₃, 1), respectively for the three moves listed above.

  1. Delete Move

     For a delete move, the acceptance probability is

     $$\begin{array}{c}{\alpha }_1=\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\beta }_{\mathbf{g}}}^{\ast },\dots )\pi ({\beta }_{g,k}^{\ast }=0\mid {\eta }_{\mathbf{g}}^{\ast })\pi ({\eta }_{\mathbf{g}}^{\ast })}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{g}},\dots )\pi ({\beta }_{g,k}\mid {\eta }_{\mathbf{g}},{\beta }_{g,(-k)})\pi ({\eta }_{\mathbf{g}})}=\\ =\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\beta }_{\mathbf{g}}}^{\ast },\dots )\mathit{Beta}(t_g-1+z_{g,1},m_g-t_g+1+z_{g,2})}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{g}},\dots )N({\beta }_{g,k}\mid {\mu }_{\mathit{old}},{\sigma }_{\mathit{old}}^2)\mathit{Beta}(t_g+z_{g,1},m_g-t_g+z_{g,2})},\end{array}$$

     where ${\mu }_{\mathit{old}}=R_{k,(-k)}{R}_{(-k),(-k)}^{-1}{\beta }_{({\eta }_g),(-k)}$ and ${\sigma }_{\mathit{old}}^2=R_{k,k}-R_{k,(-k)}{R}_{(-k),(-k)}^{-1}{R}_{(-k),(k)}$ and $R=c{\left(X_{({\eta }_g)}^t{X}_{{\eta }_g}\right)}^{-1}$.

  2. Add move

     For the add step we set ${\eta }_{g,k}^{\ast }=1$ and sample ${\beta }_{g,k}^{\ast }$ corresponding to η_g,k = 1 from $\pi ({\beta }_{g,k}\mid {\beta }_{g,(-k)},{\eta }_g^{\ast })$ and accept ${\eta }_g^{\ast },{\beta }_{g,k}^{\ast }$ with probability ${\alpha }_2^{\ast }=min({\alpha }_2,1)$ where

     $$\begin{array}{c}{\alpha }_2=\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\beta }_{\mathbf{g}}}^{\ast },\dots )\pi ({\beta }_{g,k}^{\ast }\mid {\eta }_{\mathbf{g}}^{\ast },{\beta }_{g,(-k)})\pi ({\eta }_{\mathbf{g}}^{\ast })}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{g}},\dots )\pi ({\beta }_{g,k}=0\mid {\eta }_{\mathbf{g}})\pi ({\eta }_{\mathbf{g}})}=\\ =\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\beta }_{\mathbf{g}}}^{\ast },\dots )N({\beta }_{g,k}\mid {\mu }_{\mathit{new}},{\sigma }_{\mathit{new}}^2)\mathit{Beta}(t_g+1+z_{g,1},m_g-t_g-1+z_{g,2})}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{g}},\dots )\mathit{Beta}(t_g+z_{g,1},m_g-t_g+z_{g,2})},\end{array}$$

     where we denote ${\mu }_{\mathit{new}}={\mathrm{\sum }}_{k,(-k)}{\mathrm{\sum }}_{(-k),(-k)}^{-1}{\beta }_{({\eta }_g),(-k)}$ and ${\sigma }_{\mathit{new}}^2={\mathrm{\sum }}_{k,k}-{\mathrm{\sum }}_{k,(-k)}{\mathrm{\sum }}_{(-k),(-k)}^{-1}{\mathrm{\sum }}_{(-k),(k)}$ with $\mathrm{\sum }=c{\left(X_{{({\eta }_g)}^{\ast }}^t{X}_{{\eta }_g^{\ast }}\right)}^{-1}$.

  3. Swap Move

     For the swap step, where entry j is set to 0 and k is sampled for ${\beta }_g^{\ast }$, we jointly accept ${\eta }_{\mathbf{g}}^{\ast },{\beta }_{g,j}^{\ast },{\beta }_{g,k}^{\ast }$ with probability ${\alpha }_3^{\ast }=min(1,{\alpha }_3)$ where

     $$\begin{array}{c}{\alpha }_3=\frac{L({\beta }_{g,j}^{\ast },{\beta }_{g,k}^{\ast }\mid {\beta }_{g,(-k,-j),\dots })\pi ({\beta }_{g,j}^{\ast },{\beta }_{g,k}^{\ast }\mid {\eta }_{\mathbf{g}}^{\ast },{\beta }_{g,(-k,-j)})\pi ({\eta }_{\mathbf{g}}^{\ast })}{L({\beta }_{g,j},{\beta }_{g,k}\mid {\beta }_{g,(-k,-j),\dots })\pi ({\beta }_{g,j},{\beta }_{g,k}\mid {\eta }_{\mathbf{g}},{\beta }_{g,(-k,-j)})\pi ({\eta }_{\mathbf{g}})}=\\ =\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\beta }_{\mathbf{g}}}^{\ast },\dots )\pi ({\beta }_{g,k}^{\ast }\mid {\eta }_g^{\ast },{\beta }_{g,(-k)})\pi ({\beta }_{g,j}^{\ast }=0\mid {\eta }_g^{\ast })\mathit{Beta}(t_g+z_{g,1},m_g-t_g+z_{g,2})}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{g}},\dots )\pi ({\beta }_{g,j}\mid {\eta }_g,{\beta }_{g,(-j)})\pi ({\beta }_{g,k}=0\mid {\eta }_g)\mathit{Beta}(t_g+z_{g,1},m_g-t_g+z_{g,2})}=\\ =\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\beta }_{\mathbf{g}}}^{\ast },\dots )N({\beta }_{g,k}^{\ast }\mid {\mu }_{\mathit{new}},{\sigma }_{\mathit{new}}^2)}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\beta }_{\mathbf{g}},\dots )N({\beta }_{g,j}\mid {\mu }_{\mathit{old}},{\sigma }_{\mathit{old}}^2)},\end{array}$$

     where we denote ${\mu }_{\mathit{new}}={\mathrm{\sum }}_{k,(-k)}{\mathrm{\sum }}_{(-k),(-k)}^{-1}{\beta }_{({\eta }_g),(-k)}$ and ${\sigma }_{\mathit{new}}^2={\mathrm{\sum }}_{k,k}-{\mathrm{\sum }}_{k,(-k)}{\mathrm{\sum }}_{(-k),(-k)}^{-1}{\mathrm{\sum }}_{(-k),(k)}$ with $\mathrm{\sum }=c{\left(X_{{({\eta }_g)}^{\ast }}^t{X}_{{\eta }_g^{\ast }}\right)}^{-1}$. Likewise, we define ${\mu }_{\mathit{old}}=R_{j,(-j)}{R}_{(-j),(-j)}^{-1}{\beta }_{({\eta }_g),(-j)}$ and ${\sigma }_{\mathit{old}}^2=R_{j,j}-R_{j,(-j)}{R}_{(-j),(-j)}^{-1}{R}_{(-j),(j)}$ with $R=c{\left(X_{({\eta }_g)}^t{X}_{{\eta }_g}\right)}^{-1}$.

     After we jointly accept or reject ( ${\eta }_{\mathbf{g}}^{\ast },{\beta }_{\mathbf{g}}^{\ast }$), we resample each entry of β_g|η_g conditional on the other non-zero entries and then sample β_g|η_g jointly for better mixing of our posterior distribution.

• λ_g update

  We used the same sampler as Lee et al [9] for all samplers except the birth and death of a split point in hazard g = 1, 2, 3 along with using a different proposal distribution for λ_g|s_g, μ_λg, ${\sigma }_{{\lambda }_g}^2$,Σ_λg. Recall the MVN-ICAR specification of the prior for λ_g that was imployed in Lee et al which sets up two matrices based on distances between adjacent split points [12] [9]. Formally, define ${\overline{\mathrm{\Delta }}}_j^g=s_{g,j}-s_{g,j-1}$ and let W^g be an off diagonal matrix with entries

  $$W_{j(j-1)}^g=\frac{c_{{\lambda }_g}({\overline{\mathrm{\Delta }}}_{j-1}^g+{\overline{\mathrm{\Delta }}}_j^g)}{{\overline{\mathrm{\Delta }}}_{j-1}^g+2{\overline{\mathrm{\Delta }}}_j^g+{\overline{\mathrm{\Delta }}}_{g+1}^g}\text{and}{W}_{j(j+1)}^g=\frac{c_{{\lambda }_g}({\overline{\mathrm{\Delta }}}_{j+1}^g+{\overline{\mathrm{\Delta }}}_j^g)}{{\overline{\mathrm{\Delta }}}_{j-1}^g+2{\overline{\mathrm{\Delta }}}_j^g+{\overline{\mathrm{\Delta }}}_{j+1}^g}$$
  here c_λg ∈ [0, 1] characterizes the dependence between the heights of adjacent split point intervals. In our computation, we set c_λg = 1 to encourage spatial dependency in adjacent intervals. Let Q^g be a diagonal matrix with entries $Q_j^g=2/({\overline{\mathrm{\Delta }}}_{j-1}^g+2{\overline{\mathrm{\Delta }}}_j^g+{\overline{\mathrm{\Delta }}}_{j+1}^g)$. Then we have Σ_λg = (I −W^g)⁻¹Q^q and the MVN-ICAR prior is

  $${\lambda }_g\mid J_g,{\mu }_{{\lambda }_g},{\sigma }_{{\lambda }_g}^2~N_{J_g+1}({\mu }_{{\lambda }_g}\underset{\_}{1},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g})$$
  Our sampler differs from Lee et al. [9] in that we sample our proposal ${\lambda }_{g,k}^{\ast }$ from a uniform distribution on [λ_g,k −c_g, λ_g,k +c_g] where c_g is a tuning parameter for k = 1, ...J_g +1. We set c_g = .25 as in Haneuse et al. [17]. This proposal distribution causes the proposal ratio to be 1 which leads to an acceptance probability of this move to be the minimum of 1 and

  $$\alpha =\frac{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {{\lambda }_{\mathbf{g}}}^{\ast },\dots )N_{J_g+1}({{\lambda }_{\mathbf{g}}}^{\ast }\mid {\mu }_{{\lambda }_{\mathbf{g}}},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g})}{L({\mathbf{Y}}_{\mathbf{1}},{\mathbf{Y}}_{\mathbf{2}},{\delta }_{\mathbf{1}},{\delta }_{\mathbf{2}},\mathbf{X}\mid {\lambda }_{\mathbf{g}},\dots )N_{J_g+1}({\lambda }_{\mathbf{g}}\mid {\mu }_{{\lambda }_{\mathbf{g}}},{\sigma }_{{\lambda }_g}^2{\mathrm{\sum }}_{{\lambda }_g})}$$