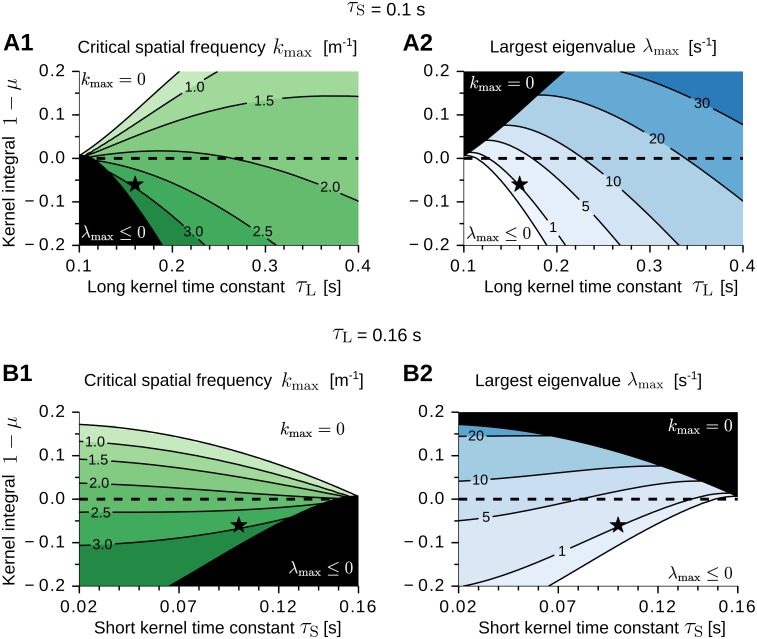
Fig 4. Impact of the adaptation kernel on grid-pattern formation.

(A1-A2) Critical spatial frequency k_max (A1) and largest eigenvalue λ_max (A2) as a function of the kernel integral 1 − μ and the long kernel time constant τ_L. The short time constant is τ_S = 0.1 s. The black lines are iso-levels (see annotated values). Regions enclosed by two adjacent iso-lines are colored uniformly (darker colors denote larger values). Within the black region in A1 we obtain λ_max ≤ 0 s⁻¹ (see white region in A2). Within the black region in A2 we obtain k_max = 0 m⁻¹ (see white region in A1). The dashed horizontal line indicates zero-integral kernels. The star denotes the parameter values τ_S = 0.1 s, τ_L = 0.16 s, μ = 1.06 of the kernel in Fig 1. (B1-B2) Same as in A but varying the short kernel time constant τ_S. The long time constant is τ_L = 0.16 s. The eigenvalue spectrum is estimated from Eq 32. Further parameter values: σ = 6.25 cm, r_av = 0.4 s⁻¹, W_tot = 1 s, ρ = 900 m⁻², L = 1 m, v = 0.25 m/s, a = 1.1 s⁻¹.