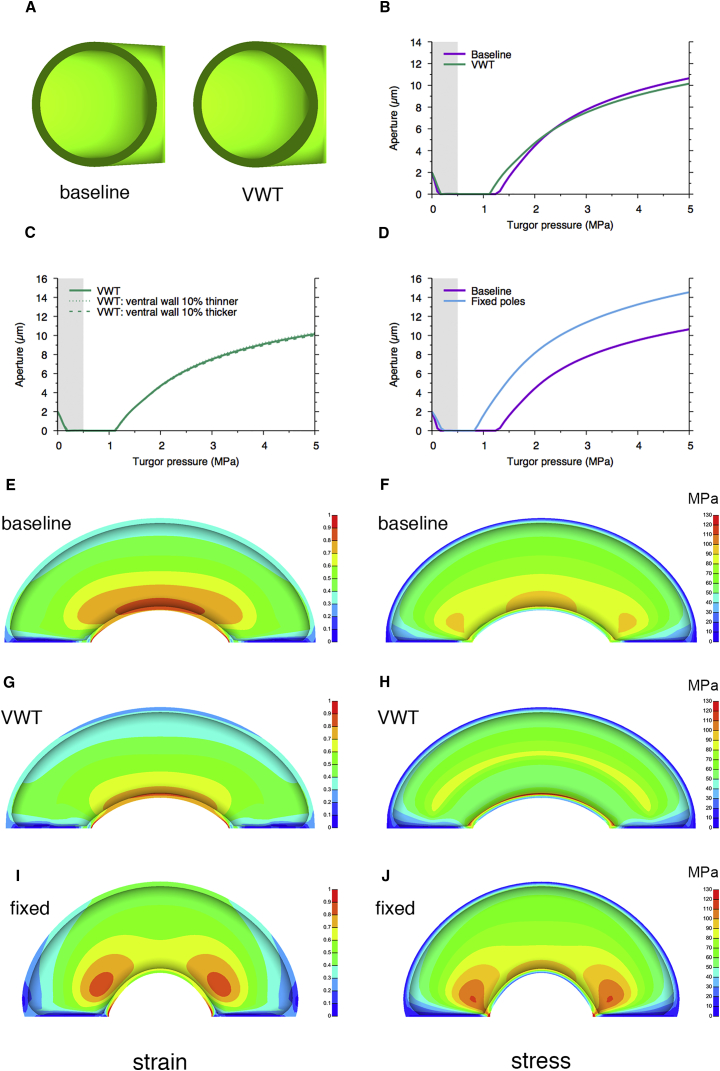
Figure 2.

Finite Element Modeling Indicates Only a Minor Role for Radial Stiffening in Stomatal Function but Demonstrates that Fixing Stomatal Poles Has a Major Influence on Aperture Response to Change of Turgor Pressure

(A) Cross-sections through guard cells modeled using the baseline parameters (circular cross-section and uniform wall thickness) or the variable wall thickness (VWT) model in which a rounded triangular geometry leads to differential inner wall thickness. The cell wall is modeled as an anisotropic material, parameterized by cellulose micro-fibrils embedded in an isotropic matrix. The micro-fibrils are oriented circumferentially in all models.

(B) Modeled relationship of stomatal aperture to guard cell turgor pressure. In the baseline model (purple), aperture increases as pressure increases above about 1.3 MPa, reaching a maximum value as pressure exceeds 5 MPa. Both epidermal and guard cell turgor are increased initially (gray area) after which only guard cell turgor increases. Modification of the model to include a VWT (shown in A) leads to a slight alteration in curve shape (green) so that opening occurs at a slightly lower turgor pressure and the maximal aperture attained is slightly lower.

(C) Exploration of the VWT model by increasing or decreasing the inner (ventral) wall thickness by 10% indicates essentially no outcome on the aperture/pressure response curve (lines superimposed).

(D) Modification of the baseline model (purple) so that the poles of the guard cells are fixed to prevent stomatal complex elongation leads to a modified output curve (blue) in which pore opening occurs at a lower turgor pressure and the final aperture attained is larger than the baseline model.

(E) Effective Lagrange strain for the inside of a guard cell modeled using the baseline parameters. The colored scale indicates the range of strain calculated in different regions of the cell, with a gradient of strain occurring across the cell radius with the inner radial wall having a high strain.

(F) Effective stress pattern in the guard cell modeled in (E). A radial stress pattern is generated with high stress at points along the inner radial wall.

(G) As in (E) but with VWT parameters used in the model. A decreased strain gradient occurs across the cell.

(H) Effective stress pattern in the guard cell modeled in (G). The stress pattern observed in (F) is dissipated so that less extreme gradients are formed, with maximal stress occurring in a medial region.

(I) As in (E) but with the stomatal poles fixed (as in D). The pattern is modified from (E) so that high strain gradients form in localized regions toward the guard cell poles.

(J) Effective stress pattern in the guard cell modeled in (I). Steeper stress gradients now form toward the guard cell poles compared to (F). In (E), (G), and (I) the strain is dimensionless and is capped at 1 for consistency across the figures. Only the regions immediately neighboring the point at which the pore adjoins the polar wall exceed this value. Strain is a dimensionless tensor describing the deformation of the material, which in simple cases is defined as length change per length. Stress is a tensor which characterizes the internal forces within a material as force per area. In (F), (H), and (J) the unit of stress is MPa, where 1 Pa = 1 Nm⁻².