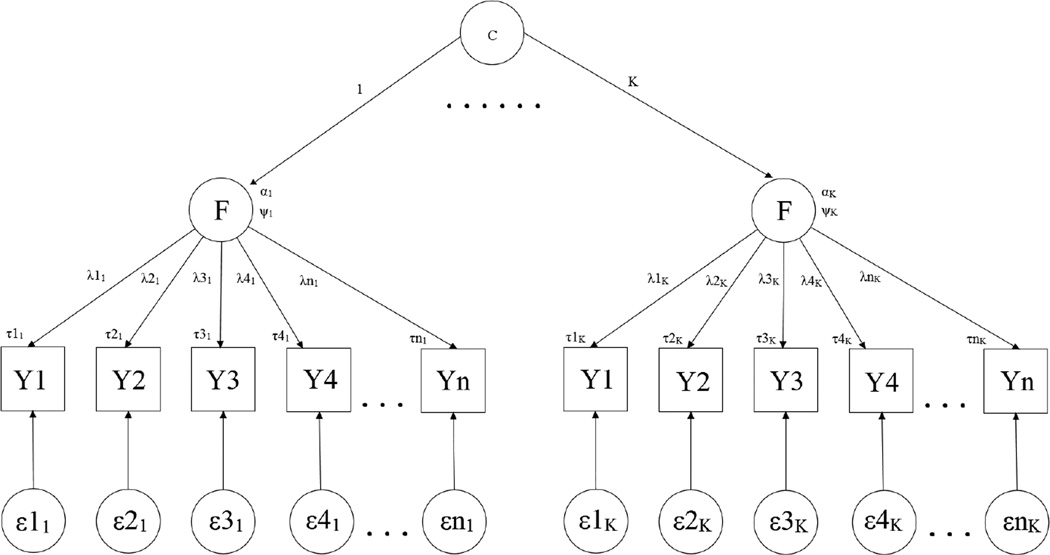
Figure 2.

Path diagram of a factor mixture model. The model includes a standard confirmatory factor model wherein a latent factor (F) accounts for the covariance among a set of observed variables (Y₁ to Y_n). The latent factor has a mean (α) and variance (σ), and in the case of models with multiple latent factors, a covariance with other latent factors (matrix Ψ). Scores on the observed variables are linked to the latent factor by a set of factor loadings (λ₁ to λ_n). A set of intercept terms (τ₁ to τ_n) models the mean structure of the observed variables, and a set of residual terms (ε₁ to ε_n) models the variance in the observed variables not accounted for by the latent factor. The factor mixture models can further model the presence of latent subgroups or classes represented by C, with 1 to K classes in the model (class is represented by the second subscript number for the factor loadings, intercepts, and residual terms). C is not a parameter that is estimated in the model; rather, the number of classes is specified by the user. Each class then has a latent factor structure, and parameters of the latent factor model can either be constrained or allowed to vary across classes.