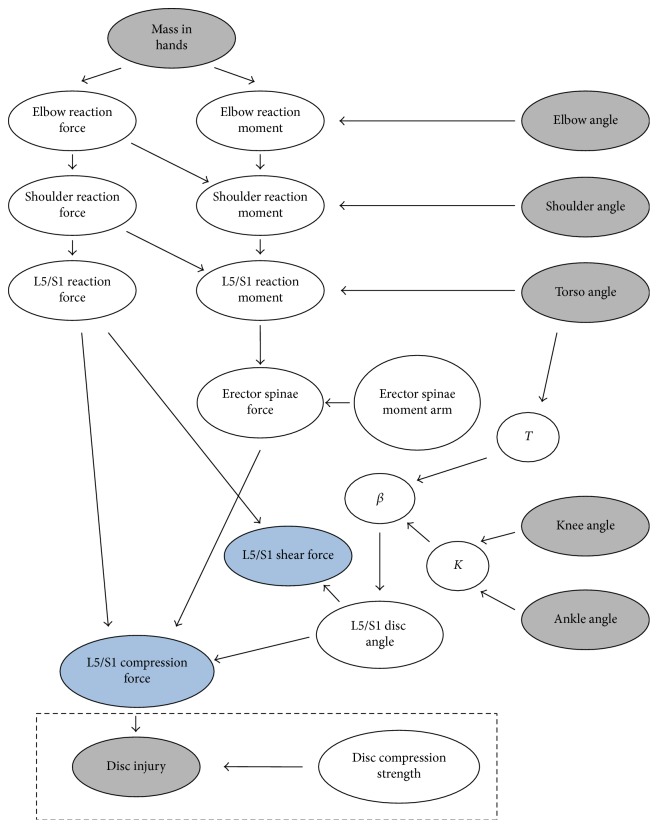
Figure 1.

Bayesian network implementation of a two-dimensional top-down lifting model described by Chaffin et al. [29] (pp. 130–134). The “basic model” is the DAG outside the dashed rectangle at the bottom; the “injury-augmented model” is the entire DAG including the two nodes and edges inside the dashed rectangle at the bottom. Input variables are represented as gray nodes (mass in hands, elbow angle, shoulder angle, torso angle, knee angle, and ankle angle). The angles are defined relative to the horizontal. Intermediate angles T (torso angle from vertical) and K (included knee angle) are computed from input angles to reduce the complexity of the expression in β, which was the deviation of the disc angle from 40°. This was done to facilitate computation. Joint reaction forces and moments are calculated for the elbow, shoulder, and L5/S1 levels because it is a top-down modeling approach. The line of action of the erector spinae muscle is assumed to be perpendicular to the L5/S1 disc, so there is no directed edge from erector spinae force to L5/S1 shear force. The erector spinae moment arm is treated as a constant (5.3 cm) and has its own node. The variables to be predicted in this model are the L5/S1 compression force and L5/S1 shear force, and they are denoted as blue nodes. The injury-augmented model was created by adding the nodes contained in the dashed rectangle (disc injury and disc compression strength); these implement the inference model of disc failure based on structural reliability modeling. Because the disc injury node was an input in the injury-augmented model, its node is shaded gray.