Brain tumor segmentation using holistically nested neural networks in MRI images

Abstract

Purpose

Gliomas are rapidly progressive, neurologically devastating, largely fatal brain tumors. Magnetic resonance imaging (MRI) is a widely used technique employed in the diagnosis and management of gliomas in clinical practice. MRI is also the standard imaging modality used to delineate the brain tumor target as part of treatment planning for the administration of radiation therapy. Despite more than 20 yr of research and development, computational brain tumor segmentation in MRI images remains a challenging task. We are presenting a novel method of automatic image segmentation based on holistically nested neural networks that could be employed for brain tumor segmentation of MRI images.

Methods

Two preprocessing techniques were applied to MRI images. The N4ITK method was employed for correction of bias field distortion. A novel landmark‐based intensity normalization method was developed so that tissue types have a similar intensity scale in images of different subjects for the same MRI protocol. The holistically nested neural networks (HNN), which extend from the convolutional neural networks (CNN) with a deep supervision through an additional weighted‐fusion output layer, was trained to learn the multiscale and multilevel hierarchical appearance representation of the brain tumor in MRI images and was subsequently applied to produce a prediction map of the brain tumor on test images. Finally, the brain tumor was obtained through an optimum thresholding on the prediction map.

Results

The proposed method was evaluated on both the Multimodal Brain Tumor Image Segmentation (BRATS) Benchmark 2013 training datasets, and clinical data from our institute. A dice similarity coefficient (DSC) and sensitivity of 0.78 and 0.81 were achieved on 20 BRATS 2013 training datasets with high‐grade gliomas (HGG), based on a two‐fold cross‐validation. The HNN model built on the BRATS 2013 training data was applied to ten clinical datasets with HGG from a locally developed database. DSC and sensitivity of 0.83 and 0.85 were achieved. A quantitative comparison indicated that the proposed method outperforms the popular fully convolutional network (FCN) method. In terms of efficiency, the proposed method took around 10 h for training with 50,000 iterations, and approximately 30 s for testing of a typical MRI image in the BRATS 2013 dataset with a size of 160 × 216 × 176, using a DELL PRECISION workstation T7400, with an NVIDIA Tesla K20c GPU.

Conclusions

An effective brain tumor segmentation method for MRI images based on a HNN has been developed. The high level of accuracy and efficiency make this method practical in brain tumor segmentation. It may play a crucial role in both brain tumor diagnostic analysis and in the treatment planning of radiation therapy.

1. Introduction

Gliomas are rapidly progressive, neurologically devastating, largely fatal brain tumors.^{1, 2} Standard therapy consists of maximal surgical resection followed by observation for younger patients with tumors having good pathologic features and concurrent radiation therapy and temozolomide (TMZ) chemotherapy followed by adjuvant TMZ in high‐grade gliomas with poor prognostic features. In glioblastoma this approach results in an overall survival of 27.2% at 2 yr and 9.8% at 5 yr.³ Magnetic resonance imaging (MRI) is a widely used technique employed in the diagnosis, management, and follow‐up of gliomas in clinical practice. Radiation therapy treatment planning employs MRI as the standard imaging modality used to delineate the brain tumor target following co‐registration with CT simulation images. Due to the high variation in brain tumor shape, size, and location, and particularly to the subtle intensity changes of tumor regions relative to the surrounding normal tissue, computational brain tumor segmentation in MRI is still a challenging task, in spite of more than 20 yr of research and development.^{1, 4} Compounding this is the understanding of the infiltrative nature of gliomas that precludes the accurate identification of subclinical disease.^{5, 6} Currently, in most clinical radiotherapy treatment planning systems, manual contouring is the de facto standard for tumor delineation. It requires an operator with considerable skill and expertise in both tumor diagnostics and in the handling of the specific treatment planning software. Consequently, manual contouring is both time consuming, and subject to large inter and intraobserver variability. Semi or fully automatic brain tumor segmentation methods could circumvent this variability in radiotherapy treatment planning and could allow for the inclusion of advanced imaging techniques that are more challenging to human interpretation, e.g., diffusion‐weighted imaging, attenuated diffusion coefficient maps, magnetic resonance spectroscopy, etc. Comprehensive reviews of existing brain tumor segmentation methods are provided by Mentz et al.¹ and Bauer et al.² Mentz et al. classified brain tumor segmentation methods into generative probabilistic based and discriminative approaches. Instead, we divided most brain tumor segmentation methods into semi and fully automatic groups.

For semiautomatic brain tumor segmentation, Guo, Schwartz, and Zhao presented a method using active contours,⁷ where an approximate region of interest surrounding the tumor mass is initially manually contoured, after which a combination of global and local active contour models are utilized to segment the hyperintense tumor. Raviv et al. developed a latent atlas‐based approach for image ensembles segmentation.^{8, 9} A manual segmentation is required to initialize level‐set propagation. Hamamci and Unal reported a method called “tumor‐cut,”¹⁰ which combines the cellular automata‐based segmentation with graph‐oriented methods. A maximum diameter of the tumor needs to be drawn by an expert to initialize segmentation. The basic set operations are utilized to combine the segmented volumes from different modalities. Moonis et al. applied the fuzzy connectedness approach for tumor volume estimation, where seed points for brain tumors need to be specified by the user.¹¹ Njeh et al. presented a graph cut distribution matching approach for glioma and edema segmentation in 3D multimodal MRI images.¹²

MRI‐based fully automatic brain tumor segmentation falls into several categories, including Bayesian and Markov random field (MRF),^{13, 14} atlas‐based registration and combination of segmentation with registration,^{15, 16, 17} statistical model of deformation,¹⁸ and support vector machine,^{19, 20} respectively. Recently, random forests (RF)^{21, 22} and convolutional neural networks (CNN)^{23, 24} have drawn more interest. Some researchers have successfully applied these two groups of algorithms to brain tumor segmentation for MRI images.^{4, 22, 25, 26, 27, 28, 29, 30} Random forests represent machine learning algorithms that allow for the tumor classification. Many decision trees are constructed during training, and a class is assigned that claims the most votes of the individual trees during testing. The strength of the RF methods includes both its capability to naturally handle multiple class of classifications and its characteristics utilizing large number of different features as the input vector. Tustison et al.²² employed RF for supervised tumor segmentation based on the feature sets of intensity, geometry, and asymmetry in multiple modality MRI images. The probability maps are initially generated from random forest models and are then used as spatial priors for a refining probabilistic segmentation based on Markov random field regularization. That algorithmic framework outperformed other methods in the Multimodal Brain Tumor Segmentation (BRATS) Benchmark challenge in the conference of MICCAI 2013.¹ Unlike RF approaches, which need variable specific features for classification, CNN‐based methods have shown the advantages with respect to learning the hierarchy of complex features from in‐domain data automatically.³¹ They are usually used in image recognition systems,²⁴ but also recently in medical image analysis. CNN‐based methods have shown effectiveness in mitosis detection in breast histologic images,³² and automatic pancreas segmentation in CT images,^{33, 34} and CT‐based lymph node detection,³⁵etc. For brain tumor segmentation, numerous CNN‐based methods have been presented in both the MICCAI BRATS 2014 challenge^{28, 36, 37} and BRATS 2015 challenge.^{4, 27, 38} Pereira et al.⁴ investigated using small 3 × 3 kernels to obtain deeper CNN, with data augmentation for brain tumor segmentation. Havaei et al.³⁹ investigated several different CNN architectures for brain tumor segmentation, which employ the most recent advances in CNN design and training techniques, like Dropout regularization and Maxout hidden units, and also incorporate the local shape of tumors as well as their context. Zhao and Jia²⁶ designed multiscale CNN for brain tumor segmentation and diagnosis, where both local and global features are incorporated in the image segmentation tasks.

Even though CNN‐based methods demonstrate a promising performance in brain tumor segmentation, there is still room for improvement. Traditional standard CNN‐based methods are typically patch‐based for both training and testing. They predict the class of a pixel by processing an M × M (e.g., 32 × 32) square patch centered on that pixel and mainly focus on local features. In addition, to achieve a satisfactory class prediction, CNN methods typically require data augmentation to generate the large number of patches as additional training sets. In this paper, we investigate the use of holistically nested neural networks (HNN)⁴⁰ for brain tumor segmentation. The HNN was initially developed for edge detection using deep CNNs. However, it has also been shown to be effective in image object segmentation^{33, 35}. The HNN method has two advantages over traditional CNN: (a) holistic image training and prediction in an image‐to‐image fashion, rather than patch‐based, where each pixel has a cost function; (b) multiscale and multilevel image feature learning based on fully convolutional neural networks and deeply supervised nets. Hence, it is not necessary for the HNN to have a significant number of training datasets. Note that currently, the HNN is used for single object segmentation, in this paper we focus on enhanced brain tumor segmentation only.

The other contribution included in this paper is landmark‐based image intensity normalization for MRI images. As mentioned in the Refs. ^{1, 4, 41}, MRI image intensity normalization plays a critical role in MRI image segmentation. In the patch‐based CNN method for brain tumor segmentation, Unlike CT images, where pixel intensity is correlated with electron density, MRI image intensity does not have a tissue‐specific physical meaning and can vary, for different image sets obtained with the same MRI protocol, from same/different scanners, and from same/different imaging centers. Most methods in the MICCAI BRATS challenges in 2013, 2014, and 2015 employed the histogram matching method⁴² for MRI image intensity normalization. Histogram matching strongly depends on the histogram shape. In some cases, this method may not work well, due to the large variability in the brain tumor in size as well as in pixel intensities that may cause a different shape of the histogram. In this paper, a novel method for image intensity normalization was developed that is simple and effective. The white matter corresponding to the highest histogram bin was chosen as the landmark. Segment linear transformation was then performed to map this landmark to the standard intensity normalization scale.

2. Materials and methods

2.A. Data

Twenty high‐grade glioma (HGG) datasets from the BRATS 2013 training data were utilized for training and testing. These data were generated on a variety of scanners with different field strengths. Testing data also include ten clinical datasets with HGG from a locally developed database. Each dataset was comprised of four MRI modalities: T1‐weighted (T1), contrast‐enhanced T1‐weighted (T1c), T2‐weighted, and T2‐FLAIR images to provide complimentary biological information. All images were co‐registered to the same anatomical reference using a rigid transform with a mutual information similarity metric implemented in ITK.⁴³ All images were skull‐stripped and interpolated to 1 × 1 × 1 mm³ voxel resolution.

2.B. Image preprocessing

In MRI image analysis, there are two common artifacts that can affect the performance of image processing algorithms. These are (a) the bias field distortion and (b) the nonphysical meaning of the MRI image intensities. The first shows a slowly varying, inhomogeneous background in an MRI image. This correction of bias field distortion has been addressed extensively and many effective methods have been developed.^{44, 45} The latter artifact implies the lack of a tissue‐specific numeric meaning of the MRI pixel intensities. The importance of handling such MRI intensity normalization has been emphasized the literature.^{4, 41, 42} In the first step of our image preprocessing, the bias field distortion in MRI images were corrected using the well‐known N4ITK method.⁴⁵ Then, the intensity of each MRI image was normalized using a novel, landmark‐based method we have developed, to make the histogram of MRI images of each modality more similar across different subjects. In this paper, the landmark is chosen as the intensity value associated with the highest histogram bin of each image (ignoring the black background), which typically corresponds to the white matter tissue since it occupies the largest volume of the brain. The MRI image and the corresponding histogram of each MRI protocol are shown in Fig. 1.

Figure 1.

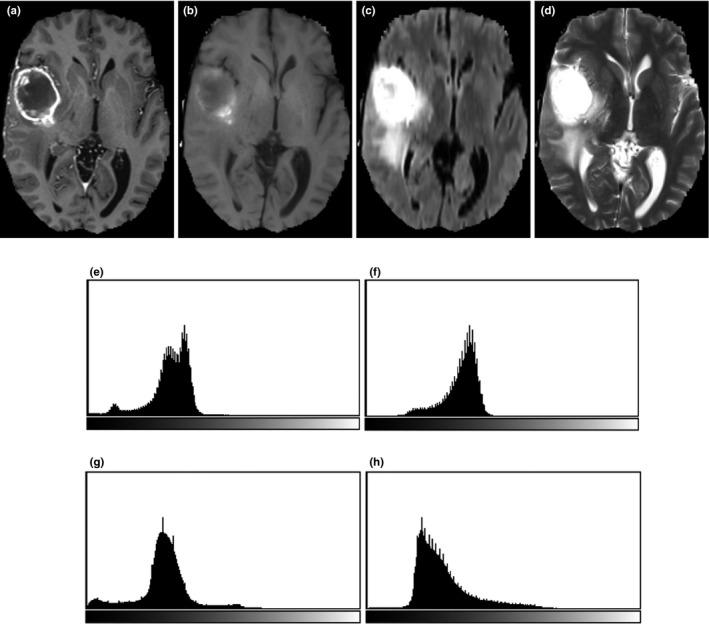
One slice of MRI images with different sequences from the BRATS 2013 one HGG patient data. (a) T1 contrast enhanced image, (b) T1‐weighted image, (c) T2 Flair image, (d) T2‐weighted image; Corresponding histograms (e) obtained from T1c, (f) from T1, (g) from T2 Flair, and (h) from T2.

Once the landmark is generated for each MRI image, a piecewise linear transform is performed by mapping the landmark intensity to the normalized intensity scale, as illustrated in Fig. 2. Here, the segment linear transformation is chosen due to its simplicity and effectiveness in producing similar histograms of MRI images across different subjects. As mentioned in the original intensity normalization paper,⁴² other transformation like using polynomial functions or split fitting techniques to stretch histogram segments may also be used, but it is out of the scope of the paper. The abscissa represents the intensities in a test image where the landmark has intensity value I_m, and the ordinate denotes the normalized reference intensities. In addition, I₁ is taken to be the smallest intensity over the test image and I₂ to be the intensity at the 99.9th percentile within the test image. Beyond 99.9 percent, the intensities represent mostly outlier values. The landmarks of I_m obtained from the histogram of each image of a subset of images are mapped to the normalized reference intensity scale by linearly mapping the intensities from [I₁, I₂] to [r₁, r₂] [e.g., (0,4095)], in such a way, the map I'_m of I_m on [r₁, r₂] can be obtained. The landmark intensity r_m on the reference scale is then determined and fixed as the rounded mean of the I'_ms. For any test image, once parameters of I₁, I₂, and I_m are obtained, two corresponding slopes of the piecewise linear transformation are calculated since parameters of r₁, r₂, and r_m on the reference scale are fixed.

Figure 2.

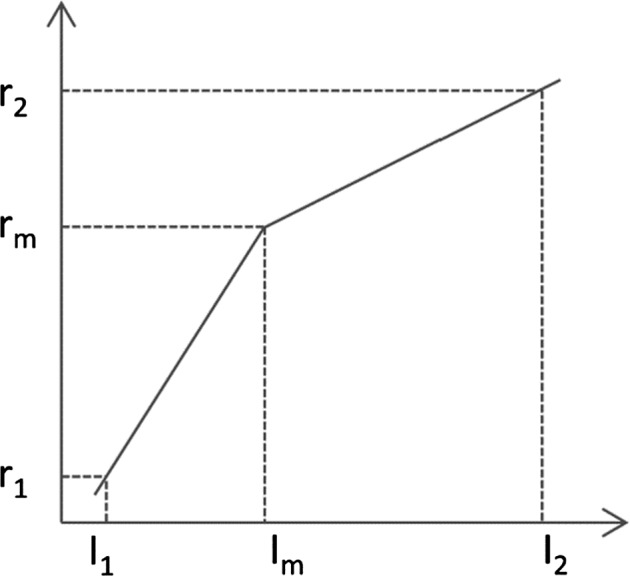
Illustration of the landmark‐based MRI intensity normalization.

2.C. Holistically nested neural networks (HNN)

Unlike traditional CNNs, which perform a pixel classification prediction using patch‐based approaches, as shown in Fig. 3(a), and make use of the local correlation between the intensities of that pixel and adjacent pixels, the HNN‐based method performs learning and prediction in an image‐to‐image fashion, by combining multiscale and multilevel hierarchical intensity representations of the image. HNN is an extension of traditional CNNs and is able to produce predictions from multiple scales. The HNN architecture comprises a single‐stream deep network with multiple side outputs, as shown in Fig. 3(b), and each corresponds to one image scale. Each side output is associated with one side‐output layer, which has a separate classifier. An additional weighted‐fusion layer is added to the HNN architecture to unify the multiple side outputs. The fusion weight parameters are learned simultaneously in the training step. In this paper, a holistic image segmentation method employing the holistically nested neural networks⁴⁰ was present for brain tumor segmentation in MRI images, wherein both training and testing take 2D MRI image slices as input. The HNN was initially developed for edge detection using deep CNNs. It has also been demonstrated that it is also effective in image object segmentation.^{33, 34, 35} The paper follows the same notation as utilized in the HNN reference paper.^{34, 40}

Figure 3.

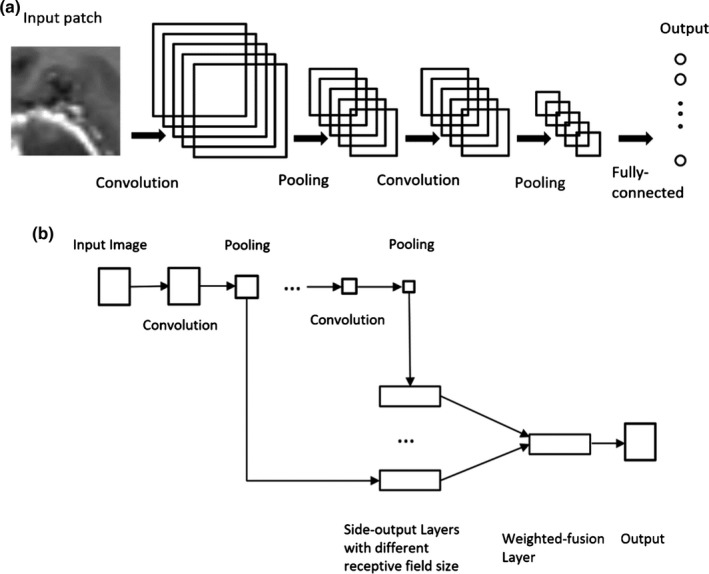
Illustration of neural network architectures: (a) Traditional CNN architecture; (b) HNN architecture.

The HNN formulation: The training data are denoted as $S=\left\{\left(X_n,Y_n\right),n=1,\cdots ,N\right\},$ where X _n denotes the input MRI image consisting of four MRI protocols, as previously mentioned in Section 2.A., and $Y_n=\left\{y_j^{\left(n\right)},j=1,\cdots ,\left|X_n\right|\right\},y_j^{\left(n\right)}\in \left\{0,1\right\}$ denotes the corresponding ground truth of the brain tumor for image X _n . In the training data, positive samples represent pixels of brain tumor and negative samples represent nontumor pixels. Suppose the collection of all standard CNNs network layer parameters is denoted as W, and we have K side‐output layers with the corresponding weights denoted by $\mathrm{w}=\left(w^{\left(1\right)},\cdots ,w^{\left(K\right)}\right)$. We then define the objective function as

$$L_{side}\left(W,w\right)=\sum _{k=1}^K{\mathit{\alpha }}_k{l}_{side}^{\left(k\right)}\left(W,w^{\left(k\right)}\right),$$

where $l_{side}^{\left(k\right)}$ denotes the image‐level loss function for the kth side‐output. In the image‐to‐image fashion training, the loss function is computed over all pixels in a training image X _n and corresponding ground truth Y _n . There is a heavy bias toward nontumor pixels in a typical MRI image with brain tumor. Therefore, to balance the loss between object and nonobject classes, an additional trade‐off parameter β is introduced by Xie and Tu.⁴⁰ Thus, a class‐balanced cross‐entropy loss function can be used in the above objective function:

$$\begin{array}{c}\hfill l_{side}^{\left(k\right)}\left(W,w^{\left(k\right)}\right)=-\mathit{\beta }\sum _{j\in Y_{+}}logPr\left(y_j=1|X;W,w^{\left(k\right)}\right)-\\ \hfill \left(1-\mathit{\beta }\right)\sum _{j\in Y_{-}}log\mathrm{Pr}(y_j=0|X;W,w^{\left(k\right)})\end{array}$$

where $\mathit{\beta }=\left|Y_{-}\right|/\left|Y\right|$ and $1-\mathit{\beta }=\left|Y_{+}\right|/\left|Y\right|$. $\left|Y_{-}\right|$ and $\left|Y_{+}\right|$ denote the ground truth set of negative and positive samples, respectively. $Pr\left(y_j=1|X;W,w^{\left(k\right)}\right)=\mathit{\sigma }\left(a_j^{\left(k\right)}\right)\in \left[0,1\right]$ is computed on the activation value at each pixel j using the sigmoid function $\mathit{\sigma }\left(·\right).$ At each side‐output layer, a single object prediction map ${\widehat{Y}}_{side}^{(k)}=\mathit{\sigma }\left({\widehat{A}}_{side}^{(k)}\right)$ is produced, where ${\widehat{A}}_{side}^{(k)}\equiv \left\{a_j^{(k)},j=1,\cdots ,|Y|\right\}$ are activations of the side‐output of layer k. An additional weighted‐fusion layer is then added to the network architecture to combine side‐output predictions. The fusion weights are learned simultaneously during the training step. The final loss function at the fusion layer is defined as

$$L_{fuse}\left(W,w,h\right)=Dist\left(Y,{\widehat{Y}}_{fuse}\right),$$

where ${\widehat{Y}}_{fuse}\equiv \mathit{\sigma }\left({\sum }_{k=1}^K{h}_k{\widehat{A}}_{side}^{(k)}\right)$ with $\mathrm{h}=\left(h_1,\cdots ,h_K\right)$ being the fusion weights. $Dist(Y,{\widehat{Y}}_{fuse})$ represents the distance between the fused predictions ${\widehat{Y}}_{fuse}$ and the ground truth label map Y, which is set to be a cross‐entropy loss. Finally, the overall objective function can be minimized using the stochastic gradient descent approach:

$${\left(W,w,h\right)}^{\ast }=\mathrm{argmin}\left(L_{side}\left(W,w\right)+L_{fuse}\left(W,w,h\right)\right)$$

In testing, for any given image X, tumor map predictions from both the weighted‐fusion layer and the side‐output layers are obtained:

$({\widehat{Y}}_{fuse},{\widehat{Y}}_{side}^{(1)},\cdots {\widehat{Y}}_{side}^{(K)})=HNN(X,{(W,w,h)}^{\ast })$, where HNN(·) denotes the object maps produced by the network. The final unified output is then produced by a further weighted averaging of all these generated prediction maps. ${\widehat{Y}}_{HED}=Average({\widehat{Y}}_{fuse},{\widehat{Y}}_{side}^{(1)},\cdots {\widehat{Y}}_{side}^{(K)}$). In this work, we take the ${\widehat{Y}}_{fuse}$ as the final prediction map. An example is shown in Fig. 4.

Figure 4.

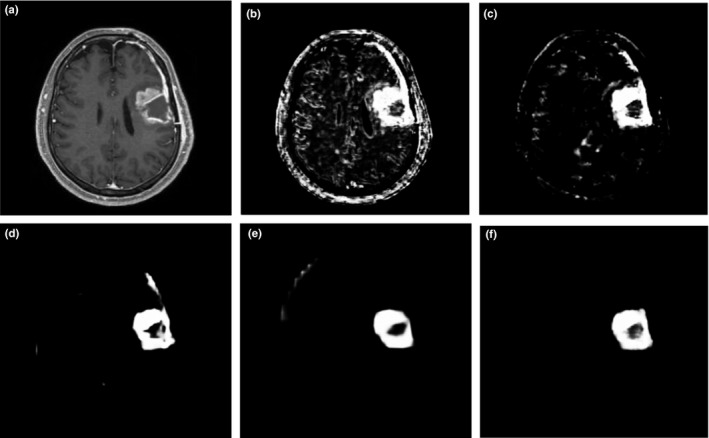
Illustration of output prediction maps. (a) one slice of the T1c component of input MRI image; and corresponding prediction maps (b) from the first side‐output layer; (c) from the second side‐output layer; (d) from the third side‐output layer; (e) from the 4th side‐output layer; (f) from the fusion layer.

2.D. Post‐processing

To produce binary segmentation results from the prediction map, a simple thresholding technique is applied. The optimal threshold value is set to maximize the mean DSC between the binary segmentation and the ground truth of the two training folds. Small connected components that are below a certain volume are discarded.

3. Results

In this section, the performance of the proposed HNNs‐based approach for brain tumor segmentation in MRI images was evaluated. As we mentioned earlier, the focused was on the enhanced tumor segmentation in this work, since the HNN is currently developed for single object segmentation, and is not able to classify the whole‐tumor region into four classes: necrosis, edema, nonenhancing tumor, and enhancing tumor. The evaluation was performed on the 20 data from the BRATS 2013 training datasets using twofold cross‐validation. These 20 HGG data are divided into two folds, each one contains ten cases. Segmentation results are produced on one fold by the HNN which was then trained on the other fold. Manual‐enhanced tumor delineations by anonymous human experts were taken as ground truths.¹ Metrics of dice similarity coefficient (DSC)⁴⁶ and sensitivity were then calculated. DSC is commonly utilized to measure the similarity between results from manual and automatic segmentation methods, and is defined as

$$\mathrm{DSC}\left(\mathrm{A},\mathrm{B}\right)=\frac{2\left(\left|A\cap B\right|\right)}{\left(\left|A\right|+\left|B\right|\right)},$$

where A represents the result from automatic segmentation method and B represents the result from manual segmentation, and $\left|\mathrm{A}\right|$ denotes the number of voxels in image A with value 1.

The DSC value is 1 when the two segmentation results are identical and 0 when they are completely disjoint.

Sensitivity is usually used to measure fraction of positives that are correctly identified by a certain segmentation method. It is defined as

$$\mathrm{Sensitivity}=\frac{TP}{TP+FN},$$

where TP represents the number of true positive and FN is the number of false negative. Measurements from the proposed method were compared with the popular fully convolutional networks (FCN) method.^{47, 48} The results of comparison are shown in Table 1. It is shown that the HNN‐based method outperformed the FCN method, on the BRATS 2013 training datasets. Note that the FCN implementation we adopted is based on the FCN‐8s network, which is publicly available at http://fcn.berkeleyvision.org. The data fed into the FCN method are those after two‐step preprocessing as described in Section 2.B.

Table 1.

Performance comparison of enhancing tumor segmentation between the proposed HNN‐based method, and the FCN method, on the high‐grade training data from the BRATS 2013

Method	DSC	Sensitivity
FCN	0.61	0.65
Proposed HNN‐based	0.78	0.81

In Fig. 5, an example of the segmentation of one HGG patient from BRATS 2013 datasets is presented.

Figure 5.

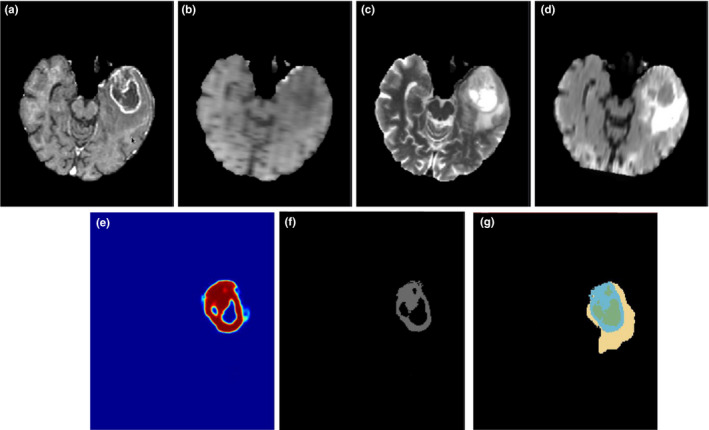
Illustration of the enhanced tumor segmentation using our proposed HNN method on one HGG patient from BRATS 2013 datasets. The four images in the first row shows the MRI modalities. (a) T1c, (b) T1, (c) T2, (d) Flair. Images in the bottom row from left to right are (e) prediction map, (f) final binary segmentation after optimal thresholding on prediction map, and (g) ground truth where light blue color represents enhanced tumor. [Color figure can be viewed at wileyonlinelibrary.com]

In addition, the proposed method was used to evaluate clinical data where the HNN was trained using the same BRATS 2013 training data. Ten patient datasets were randomly chosen with HGG from a locally developed database. Like BRATS datasets, each patient dataset consisted of four modalities: T1c‐, T1‐, T2‐, and Flair‐weighted images. Figure 6 shows an example, and Table 2 lists the measurements of DSC and sensitivity of the proposed HNN‐based method, and comparison with the FCN method. Note Ground truths in the performance evaluation were manually contoured by a clinical radiation oncologist.

Figure 6.

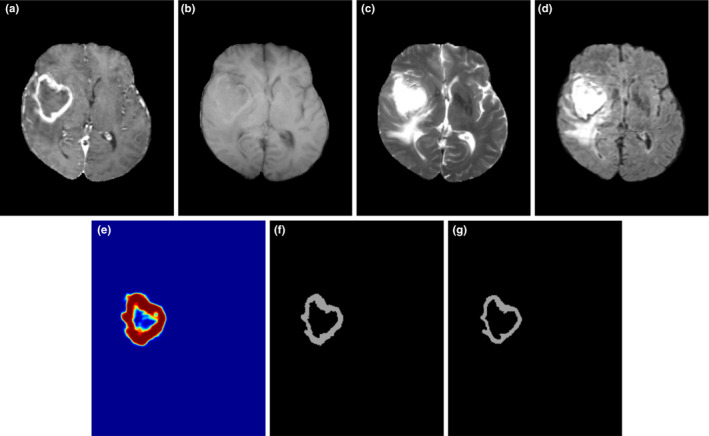
Illustration of the enhanced tumor segmentation using proposed HNN method on clinical data from a local database where the HNN is trained on BRATS 2013 datasets. (a) T1c, (b) T1, (c) T2, (d) Flair, (e) prediction map, (f) binary segmentation, and (g) ground truth. [Color figure can be viewed at wileyonlinelibrary.com]

Table 2.

Performance evaluation of the proposed HNN‐based method, and comparison with the FCN method on ten clinical datasets with HGG from a local database

Method	DSC	Sensitivity
FCN	0.67	0.70
Proposed HNN‐based	0.83	0.85

According to the results shown in Table 2, both DSC and Sensitivity of the proposed HNN method and the FCN method, on ten patient sets with HGG from a clinical database were improved relative to those of the BRATS 2013 datasets. One reason might be the difference of image quality between two datasets. The other reason could be the difference in the ground truth. Different observers have different preferences in manually contouring ground truth and these sometimes show significant variances, even on same datasets. The proposed HNN method outperformed the FCN method in terms of both the DSC and sensitivity.

The proposed HNN‐based method is implemented based on the HED system⁴⁰ using the publicly available Caffe platform,⁴⁹ and is executed on a DELL WORKSTATION T7400 with a quad‐core 2.66 GHZ Xeon CPU, with 32 GB memory under the CentOS 6.6 Linux operating system. A GPU NVIDIA Tesla K20c with 5 GB device memory was used. The program takes around 10 hr for training with 50000 iterations, and takes only around 30 s for testing of a typical image set with a size of 160 × 216 × 176. In efficiency, the proposed HNN‐based method outperforms most CNN‐based methods.^{1, 4, 36, 37} Pereira reports an average running time of 8 min for one BRATS 2013 data,⁴ on an Intel Core i7 3.5 GHz machine, using a GPU NVIDIA GeForce GTX 980. The difference in running times may be due to the processing of substantial number of patches in their method. In addition, their method adopted a different network architecture, which has more deeper layers while the proposed method only has five stages with a trimmed VGGNet network.

4. Discussion

The entire network of the HNN method is fine‐tuned from initialization based on a pretrained model VGGNet on ImageNet.⁵⁰ In this manner, multiscale and multilevel image features can be efficiently generated due to the deep architecture derived from the VGGNet. Unlike the traditional CNN networks where data augmentation is a common procedure to improve prediction accuracy,^{4, 39} the HNN does not require a large number of training datasets. In our experiments, the HNN model was trained on ten data from the BRATS 2013 datasets and can be effectively applied to segmentation on clinical datasets.

We followed the implementation of the original HED system.⁴⁰ The final network architecture has five stages, with strides of 1, 2, 4, 8, and 16, respectively, all nested in the trimmed VGGNet. In each stage, the final convolutional layer is connected to one side‐output layer with corresponding receptive field size. In addition, the same hyperparameters as the HED system are used, which include the learning rate of 1e‐6, momentum of 0.9, the loss‐weight α _k of 1 for each side‐output layer. The final fusion layer weights after network training convergence are $\mathrm{h}=\left(0.19967,0.20004,0.20070,0.20059,0.20078\right)$.

As for the image intensity normalization, in our implementation, we mapped the intensity scale of a given test MRI image to intensity range from 0 to 4095 via a piecewise linear transformation, in such a way there is less information loss during intensity normalization. The slices of a three‐dimensional MRI image were saved as a series of JPEG files with intensity scaled to range between 0 and 255. These JPEG files were finally fed into the Caffe platform. Pereira et al.⁴ reported that the metrics of DSC and sensitivity from the method (patch‐based CNN) had obtained a mean gain of 4.6% by preprocessing using Nyul's intensity normalization.⁴² It is shown that in MRI application, CNN‐based classifiers improved performance after intensity normalization. The performance difference of the proposed HNN‐based method (image‐to‐image fashion, multiscale CNN) before and after intensity normalization will be further investigated in the future.

5. Conclusions

In this paper, a novel automatic brain tumor segmentation method based on holistically nested neural networks (HNN) has been described. Two preprocessing techniques, namely Bias Field Inhomogeneity Correction and Intensity Normalization, were first applied to MRI images. Multiscale and multilevel hierarchical image features were learned through the HNN training. Unlike the traditional CNN methods which are patch‐based and mainly focus local features, the HNN method performed both training and prediction based on holistic image‐to‐image fashion.

The performance of the proposed HNN method was evaluated on 20 HGG BRATS 2013 training datasets and ten patient datasets with HGG from a clinical database. A dice similarity coefficient and sensitivity of 0.78 and 0.81 for the BRATS 2013 data, 0.83 and 0.85 for clinical data have been achieved, respectively. Thanks to the landmark‐based intensity normalization technique, the HNN training model can also be effectively utilized for testing clinical HGG data. The proposed method outperformed the FCN method based on a quantitative comparison. Note that the dice coefficient and sensitivity of the enhanced tumor segmentation produced by the state‐of‐the‐art CNN methods are 0.73 and 0.80,³⁹ and 0.77 and 0.81,⁴ respectively, on the BRATS 2013 Challenge data. Unfortunately, the HNN‐based method focused only on single object segmentation, and does not have access an online evaluation system. We are extending the HNN‐based method from single object segmentation to simultaneous multiple object segmentation. In the future, the application of the HNN‐based method on the Challenge data will be investigated so that a comprehensive comparison with the state‐of‐the‐art CNN methods can be performed. Other applications of the HNN‐based method like organ‐at‐risk in head and neck images will also be investigated. In efficiency, the HNN method is built on top of the HED system,⁴⁰ due to the efficient implementations of both the Caffe platform⁴⁹ and the HED system,⁴⁰ this method takes approximately 30 s to segment the enhanced brain tumor in a reference dataset. Both increased accuracy and efficiency make the HNN a very practical segmentation method which may play an important role in both diagnosis and radiation therapy treatment planning.