Abstract
Purpose
Catheter‐based ultrasound applicators can generate thermal ablation of tissues adjacent to body lumens, but have limited focusing and penetration capabilities due to the small profile of integrated transducers required for the applicator to traverse anatomical passages. This study investigates a design for an endoluminal or laparoscopic ultrasound applicator with deployable acoustic reflector and fluid lens components, which can be expanded after device delivery to increase the effective acoustic aperture and allow for deeper and dynamically adjustable target depths. Acoustic and biothermal theoretical studies, along with benchtop proof‐of‐concept measurements, were performed to investigate the proposed design.
Methods
The design schema consists of an array of tubular transducer(s) situated at the end of a catheter assembly, surrounded by an expandable water‐filled conical balloon with a secondary reflective compartment that redirects acoustic energy distally through a plano‐convex fluid lens. By controlling the lens fluid volume, the convex surface can be altered to adjust the focal length or collapsed for device insertion or removal. Acoustic output of the expanded applicator assembly was modeled using the rectangular radiator method and secondary sources, accounting for reflection and refraction at interfaces. Parametric studies of transducer radius (1–5 mm), height (3–25 mm), frequency (1.5–3 MHz), expanded balloon diameter (10–50 mm), lens focal length (10–100 mm), lens fluid (silicone oil, perfluorocarbon), and tissue attenuation (0–10 Np/m/MHz) on beam distributions and focal gain were performed. A proof‐of‐concept applicator assembly was fabricated and characterized using hydrophone‐based intensity profile measurements. Biothermal simulations of endoluminal ablation in liver and pancreatic tissue were performed for target depths between 2 and 10 cm.
Results
Simulations indicate that focal gain and penetration depth scale with the expanded reflector‐lens balloon diameter, with greater achievable performance using perfluorocarbon lens fluid. Simulations of a 50 mm balloon OD, 10 mm transducer outer diameter (OD), 1.5 MHz assembly in water resulted in maximum intensity gain of ~170 (focal dimensions: ~12 mm length × 1.4 mm width) at ~5 cm focal depth and focal gains above 100 between 24 and 84 mm depths. A smaller (10 mm balloon OD, 4 mm transducer OD, 1.5 MHz) configuration produced a maximum gain of 6 at 9 mm depth. Compared to a conventional applicator with a fixed spherically focused transducer of 12 mm diameter, focal gain was enhanced at depths beyond 20 mm for assembly configurations with balloon diameters ≥ 20 mm. Hydrophone characterizations of the experimental assembly (31 mm reflector/lens diameter, 4.75 mm transducer radius, 1.7 MHz) illustrated focusing at variable depths between 10–70 mm with a maximum gain of ~60 and demonstrated agreement with theoretical simulations. Biothermal simulations (30 s sonication, 75 °C maximum) indicate that investigated applicator assembly configurations, at 30 mm and 50 mm balloon diameters, could create localized ellipsoidal thermal lesions increasing in size from 10 to 55 mm length × 3–6 mm width in liver tissue as target depth increased from 2 to 10 cm.
Conclusions
Preliminary theoretical and experimental analysis demonstrates that combining endoluminal ultrasound with an expandable acoustic reflector and fluid lens assembly can significantly enhance acoustic focal gain and penetration from inherently smaller diameter catheter‐based applicators.
Keywords: acoustic, deployable, endoluminal ultrasound, fluid lens, reflector, therapeutic ultrasound, thermal ablation
1. Introduction
Endoluminal catheter‐based ultrasound applicators provide a minimally invasive option for delivering localized and spatially precise thermal therapy to tissue targets that are adjacent to body cavities or lumens. Compared to other commonly used energy sources for thermal ablation, such as radiofrequency (RF), laser, or microwave, ultrasound provides a high degree of control over the spatial deposition of energy and heating, and improved penetration for targeting deeper tissues.1 Extracorporeal high intensity focused ultrasound (HIFU) uses large focused transducer arrays (0.5–1.5 MHz) to deliver ultrasound through the body to target depths of 10–15 cm, but when applied in abdominal and pelvic sites requires a clear acoustic window between the transducer and target site for safe and effective treatment, devoid of gas‐containing tissues (lungs, bowel) or other significant tissue interfaces (e.g., soft tissue‐bone) where off‐target reflection, preferential absorption, and heating can occur.2 Catheter‐based ultrasound, while more invasive than external HIFU, can be used to target sites with limited external acoustic access and provides better volumetric energy localization.1
A wide variety of device configurations has been developed for specific endoluminal ultrasound delivery pathways.1 Endogastric placement of endoluminal devices along the upper GI tract (esophagus, stomach, or small intestines) has been developed to target esophageal,3 liver,4, 5 or pancreatic tumors.6, 7 Prostate tumors or benign prostate hyperplasia has been ablated using ultrasound devices placed in the urethra8, 9, 10, 11 or in the colorectal tract.12, 13 Endovascular devices have been developed for renal denervation14 and pulmonary vein isolation.15, 16 Endocervical devices for hyperthermia in conjunction with high‐dose rate brachytherapy for advanced cervical cancer have been investigated.17 Similar applicator configurations have also been developed for laparoscopic abdominal cavity access and ablation of renal tissue.18
While each of these endoluminal ultrasound device configurations has reported varying degrees of preclinical or clinical efficacy, there are physical limitations to current endoluminal ultrasound technology which impose practical constraints on achievable energy and thermal penetration depths. By necessity, these catheter‐based devices need to have a small diameter (~2–15 mm depending on application site1) and high flexibility in order to navigate through narrow luminal passages to reach the target site. Similarly, laparoscopic‐based ultrasound devices are restricted in diameter (< 18 mm) to minimize the incision or port size for access to the abdominal cavity.18 These requirements constrain the physical size of the integrated transducer assembly (fixed or phased array) and its effective aperture, thereby limiting acoustic output and depth of penetration typically to within 1–3 centimeters of the device.1 While this limited penetration may be appropriate for sites with shallow and small targets, greater penetration and control of the focal depth could expand the utility of endoluminal ultrasound for treating sites with larger and/or deeper targets, such as for advanced stages of liver or pancreatic cancer. Beyond simply extending the length of produced lesions, a valuable capability would be target depth specificity, whereby localized lesions could be generated at specified depths without substantial near‐field heating. This would be essential for targeting tissues with deep borders (> ~3 cm) from the luminal wall, without inducing thermal injury to the luminal wall or intervening tissues. Accomplishing such specificity requires high focal gain at target depths, which is typically precluded at focal depths beyond a few centimeters due to the small (< 2 cm) effective aperture of mounted focused transducers.19
One means of enhancing the effective aperture of radiating acoustic energy in endoluminal ultrasound, without compromising the device's ease of placement or delivery, is to integrate an expandable multicompartment balloon around the transducers that serves as an acoustic reflector. The concept of combining endoluminal ultrasound with expandable balloon reflectors was introduced by Nakagawa et al., where it was used to redirect and focus acoustic energy from a tubular transducer source to create annular ring lesions for pulmonary vein isolation.15 Their design featured a multicompartment balloon that was collapsed during device delivery and removal, and expanded at the treatment site up to a diameter of 35 mm, with the inner coupling compartment of the balloon filled with water and the outer compartment filled with CO2 gas to form the reflective interface.15 Whereas the Nakagawa et al. device used a highly precise and fixed parabolic surface geometry to create the annular ring focus, a simpler balloon geometry, such as a conical surface profile, could be combined with tubular transducer sources to redirect all energy in the forward direction of the applicator, without focusing. Reflected energy would be dispersed over a larger surface area (as a function of the reflector geometry) relative to the source, resulting in an increased effective aperture of the acoustic emission. While focusing could also be directly achieved using the reflector, as demonstrated by Nakagawa et al., it requires a more complex and geometrically precise surface profile upon inflation, which is not practically amenable to dynamic and fine adjustment in order to vary the size or depth of the focal region.
Rather than use the deployable reflector to both augment the aperture and focus the acoustic energy, focusing can be achieved using an acoustic fluid lens. Fluid lenses incorporating perfluorocarbon or silicone oil solutions have been integrated with therapeutic ultrasound sources for extracorporeal hyperthermia applications by Yoon et al.20, 21 The lens is composed of a liquid that has a different speed of sound relative to water or tissue contained by a distensible membrane, and by varying the fluid volume, the spherical radius‐of‐curvature (ROC) of the convex membrane and resulting focal length of the lens can be adjusted. This distensible spherical lens allows for dynamic adjustment of the focal depth, and serves as a simpler, albeit more limited, means of achieving dynamic focusing capabilities as compared to a 2D‐phased array source which, while permitting dynamic 3D focusing, is more expensive and technically complex to fabricate and operate.
Based upon the above concepts, the core design concept explored herein is to combine deployable acoustic reflectors and fluid lenses within an endoluminal ultrasound applicator, as a means to increase focusing and penetration depth, while maintaining a small insertion profile. The proposed assembly design, as shown in Fig. 1, consists of a central tubular (i.e., cylindrical) transducer source surrounded by a conical balloon filled with water in the interior compartment and a thin (~1 mm) air or CO2 gas filled gap between two balloon layers at its border to form a reflective surface. At the distal tip, a separate balloon compartment would serve as a plano‐convex fluid lens, with a distensible distal membrane to permit dynamic adjustment of the focal depth by changing the volume of lens fluid. The entire reflector‐lens assembly would be collapsible during device insertion and removal, and could be deployed at the target site, such as the stomach or GI tract, for treatment. This particular configuration would be end‐ or forward‐firing, emulating a larger diameter spherically focused device with the focal region in line with the longitudinal axis of the device.
Figure 1.
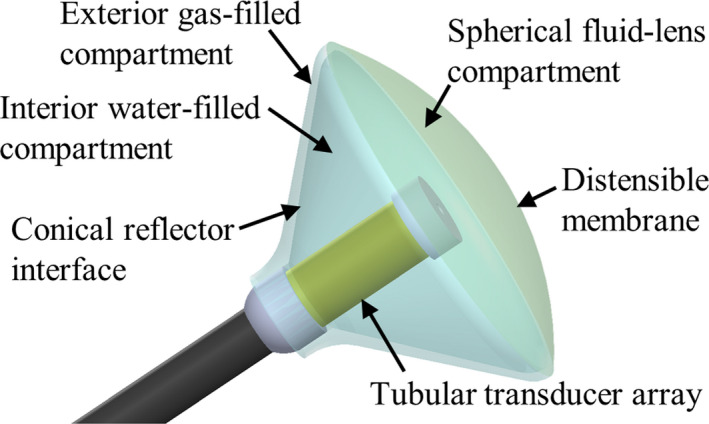
Schematic of an ultrasound applicator integrated with a multicompartment balloon that serves as a deployable acoustic reflector and fluid lens. The tubular (i.e., cylindrical) transducer is positioned centrally in a water‐filled conical balloon that has a reflector compartment, consisting of a thin air or CO 2 gas filled gap between two balloon layers, along its border. The distal compartment is filled with a perfluorocarbon or silicone oil solution, and serves as a fluid lens with a distensible distal membrane for dynamic adjustment of the focal length. [Color figure can be viewed at wileyonlinelibrary.com]
The objective of this study is to evaluate the capabilities of the proposed design and characterize its performance as a function of various design parameters, applying both theoretical and experimental approaches. Acoustic models incorporating the rectangular radiator method,22 along with the method of secondary sources,23, 24 were implemented to incorporate acoustic reflection and refraction at material interfaces. An extensive set of parametric studies over transducer, reflector, lens, and tissue properties were performed to investigate their effects on resulting acoustic pressure and intensity distributions. In order to validate the acoustic modeling methodology utilized in this study, a modular proof‐of‐concept applicator assembly was designed, fabricated, and characterized using hydrophone measurements for comparative purposes. Finally, a series of three‐dimensional biothermal simulations were performed to investigate the heating characteristics produced by the proposed design for endoluminal ultrasound ablation in pancreas and liver tissue targets.
2. Methods
Acoustic modeling of the wave propagation within and through multiple material interfaces is complex, and requires incorporation of wave reflection and refraction. Figure 2(a) shows a side‐profile schematic of the proposed applicator assembly, with ray traces to approximate how the acoustic energy propagates through each compartment of the expanded balloon. Acoustic energy would be generated by the central tubular transducer array, and emitted radially through the water‐filled interior compartment. Complete reflection would occur at the interface to the outer gas‐filled compartment, which has a 45° angle relative to the long axis of the device in order to collimate all reflecting acoustic energy along the long central axis of the device. At the interface between the water‐filled compartment and the fluid lens, partial reflection would occur due to the impedance mismatch between the two fluids. Partial reflection and refraction of the acoustic waves would occur at the distal interface of the fluid lens due to its convex surface, which focuses the beam. A thorough description of the theory and methodology employed to model acoustic propagation through the applicator assembly is given below:
Figure 2.

(a) Simplified ray traces of acoustic energy emitted by the central tubular transducer and reflected/refracted at each material interface of the applicator assembly, as numbered. Complete reflection occurs at interface 1., partial reflection at interface 2., and partial reflection and refraction at interface 3. Materials comprising each interface: 1. Water‐gas (CO 2); 2. Water‐lens fluid; 3. Lens fluid‐field medium (water, tissue). (b) Diagram for theoretical modeling of reflection and refraction at each material interface. [Color figure can be viewed at wileyonlinelibrary.com]
2.A. Acoustic modeling theory
In a homogeneous medium, the acoustic velocity potential (ψ) due to a radiating transducer source can be approximated using the Rayleigh‐Sommerfeld diffraction integral25, 26:
| (1) |
where integration is over the entirety of the radiating surface S, u [m/s] is the normal particle velocity on the radiating surface, [Np/m] is the acoustic attenuation coefficient of the medium, , k [radians/m] is the wave number, and r [m] is the distance between the field point and an infinitesimal source element of area dS. By discretizing the radiating surface into N elements of small enough area to be considered point sources, and summing the contributions from each element to the field point of interest, the expression can be evaluated as:
| (2) |
where subscript n corresponds to the nth element. The resulting acoustic pressure on a field point is23, 25, 27:
| (3) |
where [kg/m3] is the density and [m/s] is the speed of sound of the medium. If the radiating source is divided into N rectangular elements, then the rectangular radiator method22 can be used to calculate the field point pressure as:
| (4) |
where [m] is the wavelength, R n [m] is the distance from the center of the nth element to the field point, [m] and [m] are the width and height of the nth element, and [m] and y n [m] are the difference in azimuthal and elevation coordinates between the tissue point and the element center, with respect to the local orientation of the rectangular element.
In order to model wave refraction and reflection at material interfaces, the secondary source approach as applied by Fan and Hynynen23 and expanded by Moros et al.24 was employed, whereby each interface was treated as a new radiator source of a complex wave front that reflects energy back into the original medium or transmits (refracts) energy into the second medium. This method assumes plane wave theory, which was regarded as an acceptable approximation for our analysis as the distances between interfaces typically exceeded several wavelengths.23, 24 As such, it incorporates Snell's law, which relates the angles of incidence , reflection , and refraction for a wave impingent on a material interface [Fig 2(b)]:
| (5) |
As shown in Fig. 2(b), consider a ray from the nth small point source of the radiating surface traveling along to an infinitesimal area of the interface between two mediums at an angle of incidence relative to the interface surface normal. By definition, the particle velocity along can be calculated by taking the derivative of the velocity potential of the small source:
| (6) |
where [radians/m] is the wave number of the first medium. The reflected particle velocity from the interface due to the incident ray can be calculated as the particle velocity at the interface in the first medium multiplied by the velocity reflectivity , and is defined along a new direction . Hence, the normal reflected particle velocity on the interface () is the component of the reflected particle velocity along the normal of the interface:
| (7) |
where the velocity reflectivity can be calculated as:
| (8) |
Similarly, the transmitted or refracted particle velocity in the second medium is equal to the particle velocity at the interface in the first medium multiplied by the velocity transmittivity , and is defined along the direction . The normal transmitted particle velocity on the interface is the component of the transmitted particle velocity in the second medium along the normal to the interface:
| (9) |
Where the velocity transmittivity can be calculated as:
| (10) |
The reflected and transmitted normal particle velocities on the interface due to the entire radiating surface source are calculated by summing the contributions from each source element:
| (11) |
| (12) |
By discretizing the entire interface surface into M subelements, and using Eqs. (11), (12) to calculate the reflected and transmitted normal particle velocities for each element, the interface can be treated as a new radiating source. The resultant pressures in the second (or transmitted) medium can be calculated using Eqs. (2), (3) or Eq. (4), by summing over the M interface elements where n is replaced by m, the index of the mth interface element, and is replaced by , representing the transmitted normal velocity of the mth element. Similarly, the pressures in the first medium from interface reflections can be calculated using , the reflected normal velocity of the mth interface element. Further, successive material interfaces can be each regarded as secondary sources, whereby the normal velocity distributions on each interface are calculated using Eqs. (11), (12) using the reflected or transmitted normal velocity distributions of the prior interface or radiating source as the input.
Acoustic propagation through the applicator assembly was modeled by separately considering each interface as secondary sources. The interfaces, as shown and numbered in Fig. 2(a), consist of 1 — the water–gas interface between the internal and reflector compartments; 2 — the water–lens fluid interface between the internal and lens compartments; and 3 — the interface between the lens fluid and the adjacent medium in the computational field. For interface 1, the central tubular transducer is used as the radiating source to calculate the reflected normal particle velocity distribution on the conical interface. The interface is approximated as an ideal reflector, with a velocity reflectivity R of 1 and no acoustic transmission into the adjacent gas compartment. The contributions of each element of the transducer source were constrained to affect only the elements of the interface that were in front of the source element tangent plane. For interface 2, the reflected normal velocity distribution on interface 1 was used to calculate the transmitted normal particle velocities on the planar interface. Contributions from source‐interface element pairs were nullified if the ray trace between the two elements intersected with the central transducer structure. For interface 3, the transmitted normal velocity distribution of interface 2 was used to calculate the transmitted normal velocities on the convex lens surface. Following, the pressure field in the adjacent medium was calculated by discretizing the lens surface into rectangular subelements and using the transmitted normal velocity distribution as the input for the rectangular radiator method (Eq. (4)). The F value, which dictates the size of the rectangular subelements, was ≥ 150 for all simulations to ensure accuracy.22 The surface geometry of the convex lens was modeled as a spherical section, which is an appropriate approximation of the more complex parabolid geometry that characterizes fluid lenses made in practice.28
2.B. Fluid lens analysis
A theoretical analysis was used to characterize acoustic performance of the fluid lens and to compare two candidate lens fluids: perfluorocarbon solution and silicone oil. The acoustic properties each of these fluids were taken from formulations in Yoon et al.,21 and are shown in Table 1. The lens focal length, aperture diameter, and constituent fluid were all varied to investigate their impact on energy transmission across the convex lens interface. The focal length of the lens was approximated using the optical analogy for a plano‐convex lens20:
| (13) |
where ROC [m] is the radius‐of‐curvature of the lens, and and are the speed of sound of the lens fluid and water, respectively. Eq. (13) was used to determine the ROC associated with each lens focal length.
Table 1.
Acoustic properties of prospective lens fluids and water.21
| Liquid | Density (kg/m3) | Speed of sound (m/s) | Attenuation (Np/cm/MHz) |
|---|---|---|---|
| Silicone oil | 980 | 1002 | 0.055 |
| Perfluorocarbon | 1820 | 610 | 0.006 |
| Water | 1050 | 1484 | ~0 |
For the analysis, a 2D central cross‐section of the spherical lens was considered. Energy transmission across the lens was determined by calculating and summing the power transmission coefficient across the 2D section:
| (14) |
Snell's law Eq. (5) was used to calculate the relationship between angle of incidence and angle of refraction. At each point along the 2D section, the power transmission coefficient was calculated assuming a uniform and collimated energy source, such that the angle of incidence varied along the section according to:
| (15) |
where x is the x‐coordinate of the point along the 2D section, and defined as zero at the center of the lens. The maximum absolute x‐coordinate along the lens was constrained by the aperture diameter, and could not exceed the lens ROC. The sum of the power transmission coefficient across the 2D section was used to approximate the total energy transmission.
2.C. Influence of applicator design parameters on focal properties
Using the theory and methodology presented in Section 2.A., two series of parametric studies were performed to characterize acoustic output of the applicator assembly design. The first varied the expanded balloon aperture diameter [as defined in Fig. 2(b)] between 10–50 mm, the transducer radius (1–6 mm), and lens focal length (1–100 mm). For each configuration, the height of the transducer was set by the expanded balloon diameter, matching the height of the conical reflector compartment (varying accordingly between ~3 and 25 mm). These simulations were performed using a perfluorocarbon lens fluid and the resulting acoustic pressure and intensity distributions were calculated in a water medium. The time‐averaged intensity is derived from the pressure field and medium properties as:
| (16) |
Simulations were also performed for a single spherical bowl transducer (without incorporating the reflector‐lens assembly) in a water medium, to serve as a comparison and emulating a more conventional endoluminal ultrasound applicator design. The spherical transducer aperture radius was varied between 1–6 mm, and the ROC adjusted between 1–100 mm. In both cases, the transducer operating frequency was 1.5 MHz; 6 mm was chosen as the upper limit of the transducer radius in both sets of simulations as a conservative size constraint on the noncollapsible overall device profile. This upper limit would be appropriate for endogastric access, based on diameters of currently available echoendoscopes (10.5–12.8 mm) on the market.29
The second series of parametric studies investigated the effects of transducer frequency and attenuation of the field medium on achievable focal gain as a function of focal depth. A single assembly configuration was used (50 mm expanded balloon diameter, 5 mm transducer radius), while the transducer frequency was varied between 1.5 and 3 MHz, and the medium attenuation varied between 0–10 Np/m/MHz as representative of the range of attenuation coefficients in different soft tissues.30
2.D. Experimental validation
In order to validate the methodology and acoustic simulations presented herein, a proof‐of‐concept (POC) test applicator assembly was designed, fabricated, and characterized using hydrophone measurements of the beam profiles. The assembly, as shown in Fig. 3, consists of a 9.5 mm OD × 9.5 mm height 1.70 MHz tubular transducer mounted on a 3D printed housing fixture (Formlabs Inc., Somerville, MA, USA), centered in a conical brass reflector fixture. The fluid lens was made from a 3D printed fixture (Formlabs Inc., Somerville, MA, USA), with a .006” thick latex sheet (McMaster‐Carr, Santa Fe Springs, CA, USA) serving as the distal distensible lens membrane, and a .005” thick stiff polyimide sheet (McMaster‐Carr, Santa Fe Springs, CA, USA) as the proximal boundary. Fluid inlet and outlet ports were used to inject Fluorinert FC‐43 perfluorocarbon solution (Synquest Laboratories, Inc., Alachua, FL, USA) into the lens, and the radius of curvature of the latex membrane could be manually adjusted by varying the volume of perfluorocarbon in the fixture. The aperture diameter of the lens and the diameter of the brass reflector opening were 31 mm. The fluid lens fixture was centered over the applicator‐brass reflector assembly using a 3D printed adapter (Zortax, Olsztyn, Poland).
Figure 3.

(a) Cross‐sectional schematic of the proof‐of‐concept applicator assembly, consisting of a tubular transducer applicator (1.70 MHz, 4.75 mm radius × 9.5 mm height, white arrow) mounted in a brass conical reflector fixture, a fluid lens fixture filled with perfluorocarbon solution, and 3D printed adapters for mounting and alignment. (b) The applicator, brass reflector and lens fixture subassemblies are shown. (c) Acoustic characterization was performed using hydrophone scanning in a water tank, and the focal length of the lens was varied between measurements by adjusting the fluid volume in the lens fixture. [Color figure can be viewed at wileyonlinelibrary.com]
Measurements of the intensity profiles of the modular POC assembly were performed in deionized, degassed water by scanning a HNP‐0400 needle‐type hydrophone (Onda Corp., Sunnyvale, CA, USA) under computerized motor control and acquisition. A function generator (Keysight Technologies, Inc., Santa Rosa, CA, USA) and RF amplifier (Electronics & Innovation, Ltd., Rochester, NY, USA) were used to drive the transducer, with forward and reflected power monitored using a 4‐port dual directional coupler (Werlatone, Inc., Patterson, NY, USA) and inline power meter (Keysight Technologies, Inc., Santa Rosa, CA, USA). Longitudinal scanning planes through the applicator center and extending up to 90 mm in depth were obtained for a range of lens focal length, which was varied by adjusting the volume of fluid in the lens between scans. The step sizes were 0.5 mm in the transverse dimension and 1 mm in the axial dimension, and the pulse repetition period and burst count were 1 ms and 230 cycles, respectively. Peak‐to‐peak voltage measurements from the hydrophone were taken using an oscilloscope (Tektronix, Inc., Beaverton, OR, USA), and converted into time‐averaged intensity values using the acoustic efficiency of the transducer. The transducer efficiency was determined through force balance measurements31 using a bottom‐loading mass balance (Mettler‐Toledo Ltd., Leicester, UK), with the applicator‐reflector subassembly submerged in deionized and degassed water, directing acoustic energy into absorbers suspended from the balance. Acoustic simulations that modeled the POC assembly were performed for comparative purposes, but did not incorporate modeling of the thin latex or polyimide lens membranes. Percent differences between simulation and experiment in terms of the focal gain magnitude and the full‐width‐half‐max (FWHM) of the focal zone length were evaluated across focal depths ranging between ~10–65 mm.
2.E. Biothermal modeling theory
In order to investigate the utility of the proposed applicator assembly for thermal ablation of tissue, three‐dimensional bioheat transfer models of endoluminal tissue heating in liver and pancreatic tissue were employed. Transient temperature distributions resulting from the incident acoustic pressure field were simulated using an implicit finite element method solver (COMSOL Multiphysics 4.3, Comsol, Inc., Burlington, MA, USA) and the Pennes bioheat transfer equation32:
| (17) |
where [J/°C/kg] is the specific heat of tissue (for blood), [°C] is tissue temperature, [W/m/°C] is tissue thermal conductivity, [kg/m3/s] is the blood perfusion rate, is the capillary blood temperature (37 °C). [W/m3] is the acoustic heat deposition in tissue, which can be derived from the acoustic pressure field:
| (18) |
is the acoustic absorption coefficient [Np/m] in tissue, and was approximated as equal to the attenuation coefficient for each tissue as all scattered energy was assumed to be absorbed locally.
2.F. Simulated temperature distributions from deployable assemblies
A three‐dimensional model of endoluminal ablation of either liver or pancreatic tissue through the stomach wall, as shown in Fig. 4, was used. The deployable applicator assembly was situated in the stomach lumen, with the rest of the lumen filled with cooling and coupling water (25 °C). In order to constrain the parametric space, two select configurations of the applicator assembly were modeled: configuration 1 was for 30 mm expanded balloon diameter, 3 mm transducer radius × 12 mm height, sonicating at 1.5 MHz; configuration 2 was for 50 mm expanded balloon diameter, 5 mm transducer radius × 20 mm height, sonicating at 1.5 MHz. Short duration (30 s) sonications were simulated, with a constant transducer input power that was empirically adjusted to produce a maximum tissue temperature of 75 °C by the end of sonication. The maximum value of the input power was constrained so as not to exceed a transducer surface intensity of 20 W/cm2.33 The lens focal length was varied between simulations to evaluate the capability of producing selective heating at specific depths up to 10 cm.
Figure 4.
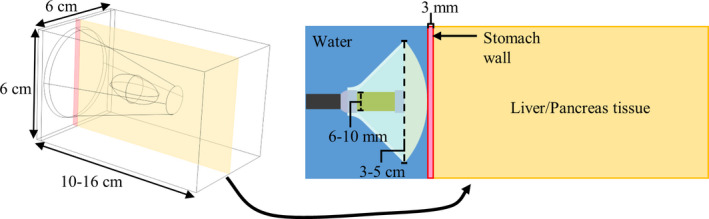
Generic tissue block model for thermal simulations of endoluminal ablation of liver or pancreatic tissue using the proposed ultrasound applicator assembly. Ranges for the dimensions for the tissue block and constituent features (transducer diameter, expanded balloon diameter) of the applicator assembly are shown. The transducer frequency was 1.5 MHz, and the radius‐of‐curvature of the lens was adjusted to target focal depths of 2–10 cm in the tissue. [Color figure can be viewed at wileyonlinelibrary.com]
For comparative purposes, simulations were also performed for a more conventional endoluminal ultrasound applicator design that contained a single 1.5 MHz, 12 mm diameter spherically focused transducer. The ROC of the transducer was varied to adjust the treatment or focal depth.
The acoustic and thermal material properties of each tissue that were incorporated in the simulations are listed in Table 2.30, 34, 35 Water cooling (25 °C) was modeled on the interior of the stomach luminal surface, by using a convective heat flux boundary equation with a heat transfer coefficient of h = 500 W/m2/°C.35 The stomach wall was modeled as 3 mm thick.36 Dirichlet boundary conditions constrained the outer borders of the tissue boundary to 37 °C. In order to simulate the dynamic cessation of perfusion during ablation, tissue perfusion was reduced from its nominal value to zero when the temperature exceeded 52 °C, which closely tracks the boundary of lethal thermal dose in these simulations.37 Borders of coagulative necrosis or thermal lesion formation by the end of the sonication were approximated by the T > 52 °C contour. Dimensions and positions of these borders are tabulated and used to assess the performance of each applicator configuration in terms of selective heating capability, penetration depth, and luminal/prefocal sparing.
Table 2.
| Tissue | Density (kg/m3) | Attenuation (Np/m) | Thermal conductivity (W/m/°C) | Specific heat (J/kg/°C) | Perfusion rate (kg/m3/s) |
|---|---|---|---|---|---|
| Pancreas | 1045 | 11.9f 0.78 | 0.51 | 3164 | 10 |
| Liver | 1050 | 6.9f | 0.51 | 3639 | 15.8 |
| Stomach wall | 1045 | 5f | 0.53 | 3698 | 6.75 |
| Blood | 1050 | – | 0.52 | 3617 | – |
f, frequency (MHz).
3. Results
3.A. Fluid lens analysis
Figure 5 illustrates how acoustic energy transmission across a fluid lens with a spherical curvature changes as a function of lens fluid, aperture diameter, and focal length. Energy transmission rises with increasing focal length up to a saturation level, and increasing the aperture size yields a greater saturation level at a higher focal length. At each focal length, there is a maximum limit of energy transmission that cannot be raised by increasing the aperture size, and that scales in magnitude with focal length. Figure 5 also shows that at all focal lengths, the perfluorocarbon fluid lens permits greater energy transmission as compared to silicone oil. The difference in transmission is relatively minimal beyond the saturation focal length for each aperture size, but is more significant prior to saturation. Hence, these results formed the basis for employing perfluorocarbon as the lens fluid in the remaining modeling and experimental work presented in this study.
Figure 5.
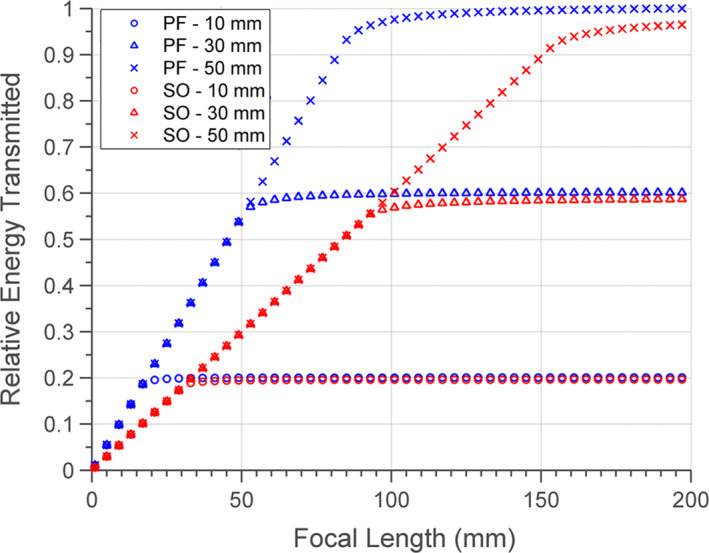
Normalized energy transmission through the convex interface of the fluid lens as a function of lens focal length, lens fluid (PF – perfluorocarbon, SO – silicone oil), and aperture diameter (10, 30, or 50 mm). [Color figure can be viewed at wileyonlinelibrary.com]
3.B. Influence of applicator design parameters on focal properties
Figures 6(a)–6(c) show three 2D planes of simulated longitudinal intensity distributions, corresponding to a single applicator assembly configuration (50 mm expanded balloon diameter, 5 mm transducer radius × 20 mm length, 1.5 MHz) at three focal depths of ~20, 40, and 60 mm in water. The scale is normalized to the input surface intensity of the tubular transducer, thus representing effective intensity gain (/). For each assembly configuration, a series of central axial intensity profiles were simulated, as demonstrated in Fig. 6(d) for the 50 mm balloon diameter, 5 mm transducer radius × 20 mm length configuration. Each individual intensity vs. depth profile corresponds to a specific lens focal length, and interpolation of the maximum gains and corresponding depths across all profiles was used to generate a general “performance envelope”. This envelope approximates the maximum achievable focal gain at each depth that could be realized by adjusting the lens curvature, and was generated for each applicator configuration.
Figure 6.
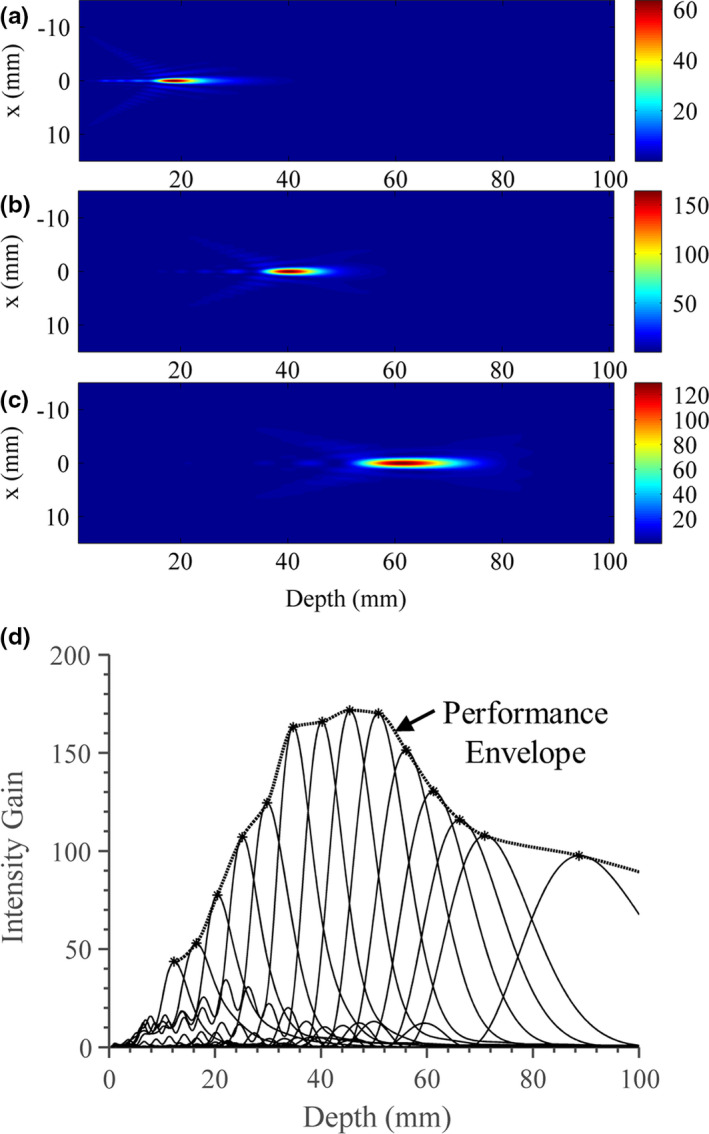
Simulated acoustic intensity gain distributions in water for the applicator assembly (1.5 MHz, 50 mm expanded balloon diameter, 5 mm transducer radius) for three separate lens focal lengths of (a) ~20 mm, (b) ~40 mm, and (c) ~60 mm. (d) A series of intensity profiles along the central axial axis (solid lines) are created by varying the lens focal length. Depth is measured as the axial distance from the lens membrane. By compiling the maximum intensity and corresponding depth of each profile, an interpolated envelope (dotted line with stars) or “performance envelope” that approximates the achievable focal gain at each depth can be determined. [Color figure can be viewed at wileyonlinelibrary.com]
A series of performance envelopes for 1.5 MHz configurations are shown in Fig. 7, with expanded balloon diameter (10–50 mm) varied between panels and transducer radius (1–6 mm radius) varied between curves. In the last panel [Fig. 7(f)], a series of simulations corresponding to a single spherically focused transducer, with varying aperture radius and ROC, is shown for comparison. It can be seen that as the balloon diameter of the applicator assembly increases, both the magnitude and the depth of the maximum focal gain increase. For all assembly configurations, the achievable focal gain generally increases as a function of focal depth up to a maximum value, then tapers down gradually. In varying the transducer radius for each balloon size, the maximum focal gain is achieved by an intermediate transducer radius value. As the balloon aperture increases, then the transducer radius that corresponds to the curve with the highest maximum gain increases as well. Comparing the applicator assembly configurations to the spherical transducer, it is evident that at very short focal depths (< 15 mm) the largest spherical transducer is capable of higher focal gains than any of the assembly configurations. However, beyond 20 mm, many assembly configurations with balloon diameters of 2 cm or greater achieve higher focal gain, with an increasing discrepancy in magnitude as the balloon size and focal depth increase. As a quantitative comparison, whereas the 6 mm radius spherical bowl transducer cannot effectively produces a focus beyond 30 mm, the assembly configuration with a 50 mm balloon diameter and 5 mm transducer radius achieves its peak focal gain of ~170 around 45 mm depth and tapers off gradually, retaining a gain of ~90 at 100 mm depth. Smaller configurations with a 10 mm balloon diameter show a maximum potential focal gains of ~6 and cannot focus beyond 2 cm.
Figure 7.
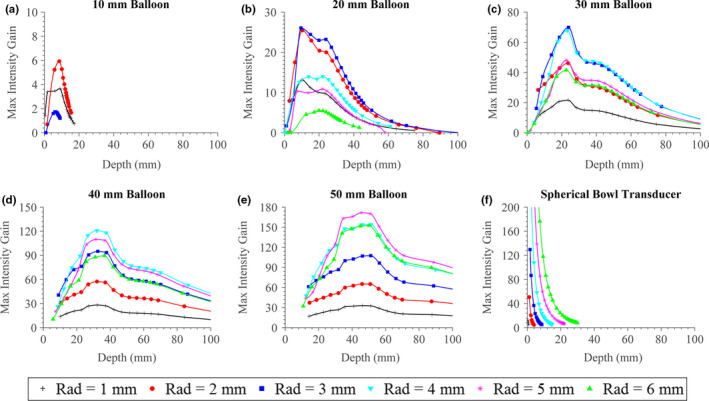
(a)–(e) Approximate maximum focal gain of the applicator assembly at 1.5 MHz operating frequency, as a function of focal depth, transducer radius (“Rad”), and expanded balloon diameter. (f) A comparative case, consisting of a 1.5 MHz spherically focused transducer of various aperture radii with curves generated by varying the radius‐of‐curvature, is shown. [Color figure can be viewed at wileyonlinelibrary.com]
The approximate sizes of the focal zone in terms of the full‐width‐half‐max (FWHM) across the axial and transverse dimensions, corresponding to the extents of the −3 dB intensity contours, are shown in Figs. 8 and 9, respectively. As expected, the axial length of the focal zone generally increases with rising focal depth, though for configurations with larger balloon apertures there is an inflection point, where the axial length only starts to increase significantly after a specific focal depth. As the balloon size increases, this inflection point translates to higher focal depths, and the overall magnitude of axial length decreases significantly (e.g., for 50 mm focal depth, the axial length is ~50 mm for configurations with 20 mm balloon diameter, and ~10 mm for 50 mm diameter). Within each balloon size, the axial length of the focal zone correlates with transducer radius, with smaller transducers producing tighter foci; this is opposite the behavior for the spherical bowl transducer. The spherical bowl transducer, compared to the tubular applicator assembly configurations, generally produces larger focal zones beyond a ~15 mm depth. The transverse width of the focal zone increases as a function of focal depth and decreases as balloon size increases, though to a lesser extent as compared to the axial length. In contrast with the axial length, the width decreases as transducer radius increases, though to a relatively minimal degree (~0.5 mm as transducer radius increases from 1 to 6 mm).
Figure 8.
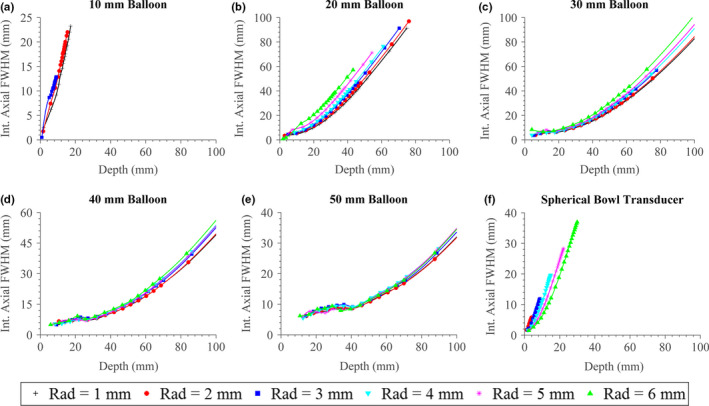
(a)–(e) Axial length of the focal zone as defined by the −3 dB intensity extents or FWHM for the applicator assembly, as a function of focal depth, transducer radius (“Rad”), and expanded balloon diameter. (f) Focal zone length for a spherically focused transducer with varying radius and radius‐of‐curvature. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 9.
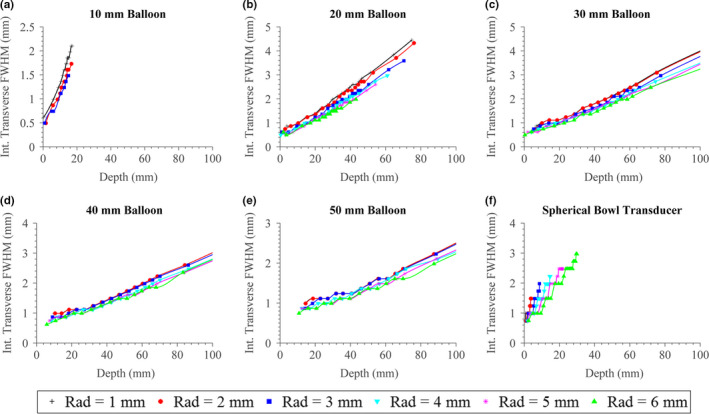
(a)–(e) Transverse width of the focal zone as defined by the −3 dB intensity contours or FWHM for the applicator assembly, as a function of focal depth, transducer radius (“Rad”), and expanded balloon diameter. (f) Focal zone width for a spherically focused transducer with varying radius and radius‐of‐curvature. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 10 shows the results for the second series of parametric studies for a single deployable configuration (50 mm balloon diameter, 5 mm transducer radius × 20 mm height), with the transducer frequency and attenuation of the medium varied. As expected, increasing the frequency results in tighter foci, with shorter −3 dB axial and transverse extents and greater focal gains in nonattenuating mediums. As the medium attenuation increases, then the lower frequency assembly is capable of producing greater gain at longer focal depths, whereas the higher frequency provides greater gain at shorter depths.
Figure 10.

Effects of transducer frequency, tissue attenuation, and focal depth on the maximum (a) focal gain, (b) axial length, and (c) transverse width of the focal zone for an applicator assembly configuration with a 50 mm expanded balloon diameter and 5 mm transducer radius. [Color figure can be viewed at wileyonlinelibrary.com]
3.C. Experimental validation
Figure 11(a) shows beam‐plots created from scanning hydrophone measurements of the test applicator assembly in a water tank. Each contour plot shows the normalized pressure‐squared distributions along longitudinal scanning planes along the central axis, with the transverse origin at the center of the fluid lens and the depth origin situated ~1 mm axial from the lens membrane. Four distributions are shown, each obtained using a different volume of lens fluid injected into the fluid lens to alter its distal curvature and effective focal length. These plots (a–d) show focal depths between ~1 cm and ~5 cm, and illustrate broadening of the axial length of the focal zone as the lens volume is reduced and focal depth increases.
Figure 11.
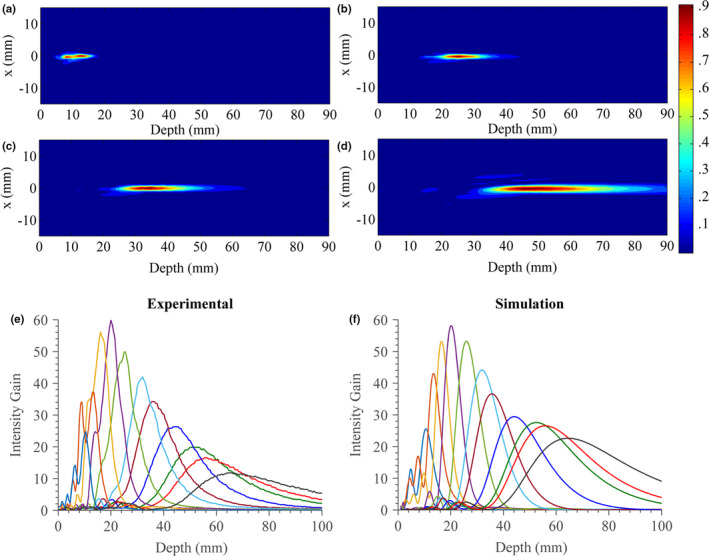
(a)–(d) Normalized beam plots (pressure‐squared distributions) measured by hydrophone in water for the experimental test applicator assembly at increasing focal lengths or distensions of the fluid lens. (e) Measured and (f) simulated central axial intensity gain profiles at a range of focal lengths. [Color figure can be viewed at wileyonlinelibrary.com]
A series of central axial intensity profiles were measured for the test applicator assembly across eleven distinct focal depths by varying the lens fluid volume. The measured profiles are shown in Fig. 11(e) and the corresponding simulated intensity gain profiles that model the test assembly in Fig. 11(f). Overall agreement between the experimental and theoretical profiles and trends is good, though discrepancies are present, particularly at the near or far limits of the focal depth. The overall percent differences between measured and simulated focal gain magnitudes and axial length FWHM of the focal zone were calculated to be 15.2% and 15.4%, respectively. In terms of focal gain magnitude, the percent difference was found to be 2.9–13.7% between 10 and 45 mm focal depths, and 28.3–47.8% between 52 and 65 mm. In terms of axial length FWHM of the focal zone, the percent difference was found to be 0.7–14.9% between 20 and 65 mm focal depths, and 29.8–55.7% between 10 and 20 mm.
3.D. Simulated temperature distributions from deployable assemblies
Figure 12 shows simulated temperature distributions in liver tissue after 30 s sonication using an ultrasound applicator assembly (50 mm balloon diameter, 5 mm transducer radius × 20 mm height, 1.5 MHz) at four distinct lens focal depths of ~20, 40, 60, and 80 mm [Fig. 12(a)–12(d) respectively]. Contours that approximate ablation boundaries of T = 52 °C and a safety margin of T = 43 °C are included. These plots illustrate selective and localized temperature rise up to the set‐point temperature (75 °C) at the each of the target depths with minimal prefocal heating.
Figure 12.
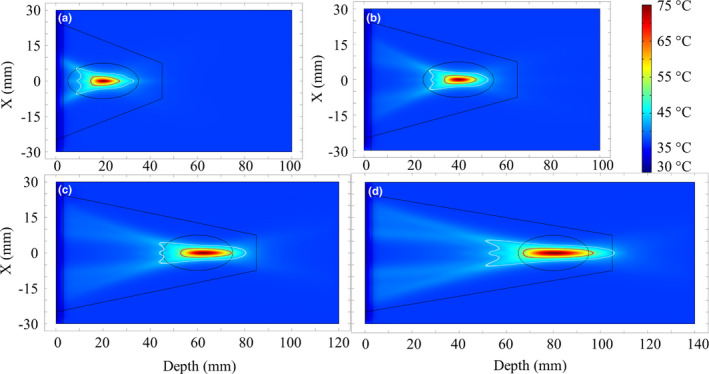
Simulated temperature distributions after 30 s sonication durations in liver tissue using the applicator assembly (1.5 MHz, 50 mm expanded balloon diameter, 5 mm transducer radius), for four separate treatment target depths of (a) 2 cm, (b) 4 cm, (c) 6 cm, and (d) 8 cm. The red (or dark grey) contour (T = 52 °C) approximates the ablated lesion borders, while the white line demarcates a T = 43 °C safety margin. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 13 compiles thermal simulation data regarding the dimensions and position of the ablation zones (T > 52 °C) in liver and pancreatic tissues as a function of target depth for each applicator assembly configuration, and compared with a 12 mm diameter spherically focused transducer. Comparing the two assembly configurations, the larger (50 mm balloon) configuration produces deeper and more localized lesions compared to the 30 mm balloon configuration. In liver tissue, the ablation volume increases from ~90–480 mm3 as target depth increases from ~20–100 mm, and from ~75–910 mm3 over ~20–70 mm target depths, for the larger and smaller assembly configurations, respectively. These volume increases primarily correspond to lengthening of the axial extents of the lesion from ~12–42 mm and ~12–56 mm, whereas the transverse widths increase from ~3.5–4.5 mm and ~3.3–5.6 mm, respectively, over the corresponding depth ranges. The nearest border of the ablated region, marking the depth in tissue to the lesion boundary, increases from ~15–83 mm as target depth increases from 20–100 mm for the larger configuration, and from ~15–48 mm over a target depth range of ~20–70 mm for the smaller configuration, with the differences from the target depth increasing at deeper depths. The maximum target depth for the smaller configuration was limited to 70 mm due to insufficient focal gain to reach a maximum temperature of 75 °C within the time/power constraints at deeper depths. Similar trends can be seen for ablation in pancreatic tissue, which primarily represents a more attenuating medium (16.3 Np/m for pancreas vs. 10.3 Np/m for liver at 1.5 MHz). This translates to more prefocal heating at deeper targets and shallower lesion depths; nearest lesion borders are up to ~3 mm shallower at an 80 mm target depth for the larger configuration, and up to ~10 mm shallower at a 50 mm target depth for the smaller configuration. The lesion volumes in pancreas are also greater by ~20–100 mm3 over 20–80 mm target depths and by ~25–140 mm3 over 20–50 mm depths for the larger and smaller configurations, respectively. For the larger configuration, significant prefocal heating occurs and creates a much larger ablation volume of ~2000 mm3 with near lesion borders at 5 mm at 100 mm target depth, while similar heating behavior and an ablation volume of ~3000 mm3 was observed for the smaller configuration at 60 mm target depth. As such, 100 mm and 60 mm approximate the focal depth limits at which the two assembly configurations can no longer create localized thermal lesions in pancreatic tissue.
Figure 13.
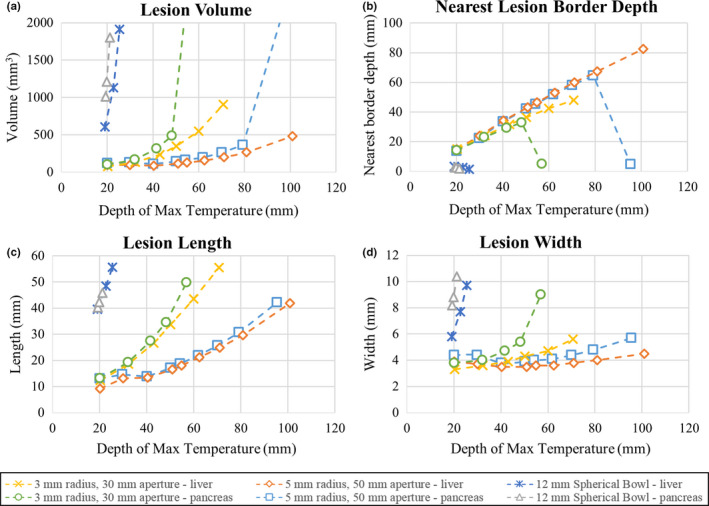
Results of thermal simulations using two select applicator assembly configurations (1.5 MHz, 30/50 mm expanded balloon diameter, 3/5 mm transducer radius) in endoluminal ablation of pancreatic or liver tissue across a range of target depths. Sonications were 30 s long with a maximum temperature of 75 °C, and lesion boundaries were approximated by the 52 °C boundaries. Comparison cases using a single 12 mm diameter spherically focused bowl transducer in liver and pancreatic tissue are also shown. [Color figure can be viewed at wileyonlinelibrary.com]
Figure 13 also includes comparative biothermal simulations of a spherical transducer with a 6 mm aperture radius and 1.5 MHz operating frequency. In liver tissue, the depth of maximum temperature, which approximates the focal depth, could not exceed ~25 mm. Due to the much more limited focusing capabilities at depth, the resultant ablation volumes were larger (up to ~1900 mm3 at a 25 mm target depth). At this largest limit, the axial length of the lesion extended up to 55 mm, and its nearest border depth was 1.6 mm, which was within the stomach wall layer. Similar volumetric performance was seen in ablation of pancreatic tissue; however, the axial length of the lesion peaked at 45 mm due to the higher attenuation, and correspondingly the depth of maximum temperature could not exceed ~22 mm. Greater heating in the transverse extents was observed, along with very shallow (< 3 mm) depths to nearest borders of the thermal ablation zone.
4. Discussion
This study has introduced and investigated design concepts for a catheter‐based ultrasound applicator assembly that incorporates deployable acoustic reflector and fluid lens components within an expandable multicompartment balloon, with potential to increase the therapeutic aperture and enhance focal gain and penetration depth. A specific design for a “forward‐ or end‐firing” applicator has been presented and acoustic simulations were employed to characterize and assess the capabilities of the proposed applicator and to determine the influence of key design parameters. The acoustic modeling methodology and simulations were in part validated by constructing a test applicator assembly and comparing hydrophone measurements of beam distributions to simulations. Finally, a series of biothermal simulations were performed and demonstrated capabilities of select assembly configurations to create selective and localized temperature rise at a range of depths (2–10 cm), for endoluminal ablation applications in either pancreas or liver tissue targets, while sparing the intervening luminal wall.
4.A. Fluid lens analysis
The trends seen in the theoretical model for energy transmission across a convex fluid lens interface offer insight toward optimal design practices concerning the fluid lens. As seen in Fig. 5, the energy transmission increases as the lens focal length increases due to the lessening of the radius of curvature of the lens surface; this results in smaller angles of incidence for the incident acoustic rays, and therefore lower reflection. This property also explains the saturation of energy transmission for a particular aperture size at long focal lengths, as the lens asymptotically flattens, leading to normal incidence of all incoming rays across the surface. Furthermore, the maximum transmission of energy at each lens focal length can be attributed to the critical angle. Once the angles of incidence for acoustic rays at the lens’ periphery exceed the critical angle, then no additional energy transmission can be realized by increasing the aperture. Instead, increasing the aperture beyond that threshold would decrease transmission due to the higher profile and subsequent greater attenuation of the fluid lens. In terms of constituent lens fluids, the perfluorocarbon solution was shown to achieve better transmission compared to the silicone oil (Fig. 5), especially at lower lens focal lengths (before saturation). This performance difference can be primarily attributed to the much lower speed of sound of perfluorocarbon relative to silicone oil (610 m/s vs. 1002 m/s), as this translates into a significantly larger radius of curvature for each focal length, permitting greater transmission due to the smaller angles of incidence. At very high focal lengths, where both lens fluids converge toward flat interfaces, the transmission difference is minimal, and solely due to the relatively small difference in acoustic impedance between the two fluids. Other studies21, 28 involving acoustic fluid lenses have indicated preference of silicone oil over perfluorocarbon due to its lower density, which is close to water. In those studies, the high density of perfluorocarbon was predicted to cause buckling or distortion of the lens profile due to gravitational forces acting on the lens fluid volume; however, the lens sizes were much larger (> 10 cm diameters) and would be more susceptible to that issue. For the experimental lens evaluated in this study, which was about ~3 cm in diameter, no significant distortion of the lens due to buoyancy forces was observed. Additionally, the membranes which make up the lens boundary can be made from less compliant materials to better maintain shape. Other desirable qualities for the lens fluid would include low acoustic attenuation, which again favors perfluorocarbon over silicone oil, as well as biocompatibility and high temperature stability.
4.B. Focal performance
Both the acoustic simulations and preliminary experimental investigations performed within this study illustrate that there is a complex relationship between the achievable focal gain and target focal depth for the proposed applicator design. The general trend shows that as target depth increases, the focal gain generally rises to a maximum then decreases beyond that corresponding depth (Figs. 7 and 11). The explanation for this trend is that there is a fundamental tradeoff between increasing the energy transmission through the fluid lens, or equivalently the effective aperture of the lens, and the inherent loss in focal gain, both caused by increasing the focal depth. At short focal depths, the increase in energy transmission or effective aperture of the lens outweighs the losses caused by increasing the focal depth, causing an upward slope in gain vs. depth. The maximum gain and corresponding depth mark the transition point, beyond which the losses exceed the increase in lens energy transmission as focal depth increases further. Whereas Fig. 5 predicts smooth increases in energy transmission as the focal length increases, the changes in achievable focal gain with depth (Fig. 7) appear to be more irregular and erratic. One possible reason for this discrepancy is that the modeling used in the energy transmission analysis (Fig. 5) assumes a uniform acoustic source, whereas the actual distribution of acoustic energy reflecting off of the conical interface is nonuniform. As such, the increase in energy transmission would be expected to fluctuate more with increasing focal length, and varies based on the transducer size and frequency, as shown in Figs. 7 and 10. The acoustic simulations were compared to hydrophone measurements of the experimental test fixture, and demonstrated good agreement in terms of the relationship between intensity gain and focal depth, as described above. The differences between the experimental assembly beam plots and theoretical simulations, while relatively minimal near the apex of focal gain, were more substantial at the low and high focal depth extremes. Discrepancies at the low focal length limit can likely in part be attributed to the extreme distension of the lens at the short depths, which would break the validity of assuming a spherical geometry. At the upper focal depth limits, the progressive thickening of the lens membrane and corresponding increase in attenuation due to reduced distension at lower fluid volumes may have contributed to the more rapid decrease in focal gain magnitude observed experimentally.
The expanded balloon size, transducer dimensions, and transducer operating frequency all have significant impact on the predicted achievable focal gain (Figs. 6, 7, 8, 9, 10). Increasing the balloon size resulted in greater focal gains, with large increases primarily at greater focal depths. Larger transducer sizes, conversely, did not always result in more focal gain. This is because for a set balloon diameter, increasing the transducer results in a smaller effective aperture, since the transverse footprint of the transducer on the lens surface is blocked. This is particularly consequential since the footprint covers the center of the lens, which has the greatest transmission, particularly at shallow focal depths. As such, there is a tradeoff between the amount of energy emitted by the transducer, which increases with larger transducers, and the effective aperture size, which increases with smaller transducers. In order to offset the blocking issue and increase gain at smaller focal depths, it may be possible to incorporate a flat disk transducer on top of the tubular transducer at the distal tip of the housing fixture, though this would add complexity and potentially increase near‐field heating. An alternative means of increasing gain, as shown by Fig. 10, would include increasing the transducer frequency, though medium attenuation must be accounted for in choosing the optimal frequency for a specific target depth.
4.C. Ablation performance
The deployable applicator design is capable of generating ablative temperature distributions in a localized and selective fashion across a large range of target depths (Figs. 12 and 13). It is important to note that the scope of the biothermal simulations performed in this preliminary study emphasized the demonstration of localized heating at specific target depths, and hence treatment parameters, including power, sonication duration, and set‐point temperature, were tailored for this purpose. More volumetric heating could potentially be achieved with the applicator assemblies than demonstrated, by adjusting the sonication parameters (lower power, longer duration). More extensive biothermal modeling analysis that incorporates additional assembly configurations, operating frequencies, and tissue dimensions and properties could also be performed to further evaluate the design and determine optimal configurations for specific target applications. In comparing the heating performances of the two select assembly configurations, the larger configuration (50 mm balloon diameter, 5 mm transducer radius) is capable of creating more selective lesions across a greater range of ~20–100 mm treatment depths in liver, as compared to the smaller configuration (30 mm balloon diameter, 3 mm transducer radius) which could produce focal heating at depths up to ~70 mm. Both assemblies exhibited greater spatial selectivity, penetration depth, and luminal sparing as compared to the 12 mm diameter spherically focused transducer (Fig. 13). Furthermore, comparisons between simulations in pancreatic and liver tissue indicate that the applicator assembly configurations achieve greater performance consistency across tissues with different material properties, particularly at moderate tissue depths (~20–80 mm and ~20–50 mm for the larger and smaller configurations, respectively), as compared to the spherically focused transducer. The performance in “liver” and “pancreas” can also be generalized as possible in other similar target tissues. Some comparisons can be drawn between the simulations of the proposed applicator assemblies and experimental evaluations of ultrasound applicators developed for endoluminal ablation of liver or pancreatic tissue, as described in literature.4, 6, 7 Collectively, these applicators had ~12 mm profiles, were placed in the stomach in in vivo porcine studies, and could create thermal lesions of ~1–2 cm maximum penetration into the target liver/pancreatic tissue.4, 6, 7 Evidence of thermal injury to the outer stomach wall was reported for each device configuration.4, 6, 7 As such, the biothermal simulations performed in this study suggest that the proposed applicator assemblies could provide substantial improvements in penetration depth and luminal sparing over these existing designs for endoluminal pancreas/liver ablation.
4.D. Fabrication and practical considerations
In realizing the proposed deployable assemblies in practice, both the interior conical balloon, whose boundary serves as the reflector, as well as the distensible lens compartment may require high precision requirements in terms of the surface geometries and mounted orientations relative to the ultrasound source. These requirements and associated manufacturing tolerances could be potentially elucidated in simulation studies that explore varying degrees of “nonideal” surface geometries or lens aberrations. With regards to the inner compartment balloon, precisely preshaped noncompliant medical balloons have been demonstrated and used in a variety of catheter‐based medical applications, such as stent/heart valve delivery or angioplasty, with many different balloon shapes and materials (PET, Nylon, etc.) possible.38 Further, precisely shaped noncompliant balloons with a reflective multilumen compartment or coating have been demonstrated and integrated with ultrasonic and fiber optic sources, respectively.15, 39 Greater technical difficulty may be associated with the integration and controlled distension of the convex lens. Bonding the distensible membrane to the noncompliant balloon could potentially be achieved using thermoplastic welding techniques (e.g., laser, RF) or with flexible medical‐grade adhesives to preserve compact collapse.40, 41 Material selection and thickness tolerance for the lens membrane will be important to ensure bonding compatibility and predictable distension behavior. As a simpler design alternative to the separate distal fluid lens compartment, the interior conical balloon could be filled with lens fluid rather than water and its distal boundary modified to a fixed‐shaped spherically convex geometry. This design would preserve effective aperture and focal gain enhancement for a set focal length, as defined by the convex boundary curvature, at the loss of dynamic adjustment to the target depth. In order to form the separate luminal compartment for gas‐backing at the conical reflector interface, noncompliant or compliant balloon materials could be bonded to the interior balloon with a gas‐filled offset or gap from the conical interface, or with a separate fluid path to inflate and distend the exterior boundary slightly with gas during deployment.
Beyond their fabrication, there are additional practical considerations with regards to utilizing the deployable reflector‐lens applicator assemblies in an in vivo setting. Navigational guidance and verification of both device placement and full deployment of the balloon assembly could potentially be achieved using MRI or ultrasound‐based image guidance, or through concurrent endoscopic visualization. MR thermometry or ultrasound tissue echogenicity changes could also be employed for treatment monitoring, as well as for targeting sequential sonications similar to extracorporeal and endorectal HIFU systems. As the geometrical integrity of the balloon is likely critical for operation, any distortions induced by contact with adjacent lumens could impact performance. This would be a particular concern for the distensible lens fluid compartment. One way to mitigate contact between the lens and the adjacent tissue, without compromising acoustic coupling and transmission into the tissue target, would be to fill the luminal space with fluid. Alternatively, an additional large expandable balloon could be integrated on the tip of the applicator (surrounding the entire multicompartment assembly), and filled with degassed water once the device is placed to conform to the luminal space and provide acoustic coupling so the deployed applicator can be used without direct tissue contact. Lens distortion could also be mitigated by incorporating a less compliant membrane material that requires high pressure for distension. During device deployment and operation, the presence of bubbles in either the interior water compartment or the lens compartment could hinder performance by causing unwanted reflections. Similar strategies as applied for other catheter‐based ultrasound applicators, including degassing all compartment fluids and evacuation of air from balloon lumens prior to device insertion could be employed. During sonication, heating of the transducer or applicator structure due to transducer operation and errant beam reflections could be mitigated by circulating cooled water through the interior compartment.
4.E. Anatomical targets and applications
The demonstrated capabilities of the deployable reflector — lens applicator assembly could enable tissue targets that were previously untreatable with catheter‐based ultrasound intervention. This fundamental forward or end‐firing design lends itself toward particular endoluminal or laparoscopic sites and delivery pathways. Endogastric placement of the applicator into the stomach or upper GI tract is particularly appropriate due to the large luminal volume once positioned within these structures, permitting insertion diameters as large as 15 mm for initial placement and deployment of the expandable balloon assembly up to and potentially beyond a 5 cm diameter. Fine positioning and manipulation of the applicator assembly could be achieved by incorporating articulation and positional control mechanisms commonly employed in endoscopic devices. From these sites tumor targets in the liver or pancreas would be most accessible; however, tumors in the gall bladder or biliary tract, kidneys or spleen, while less common and farther in anatomical proximity, could also potentially be targeted. This applicator assembly could also be suitable for laparoscopic access and ablation of tumors (such as fibroids or renal targets), permitting a minimal access port (incision) diameter and large balloon expansion within the abdominal cavity. Besides tumor ablation, another potential application could be nerve ablation for pain palliation, with the celiac plexus bundle serving as one candidate target. Other potential delivery pathways beyond endogastric or laparoscopic routes include colorectal, bronchial, and endovascular lumens. For more constricted lumens, assembly configurations with smaller profiles (~3–6 mm transducer/catheter diameter) and potentially higher operating frequencies that expand up to 10–20 mm may be particularly suited for targeting shallow (1–3 cm) treatment depths.
Lastly, it is important to note that the core concepts introduced in this study — integrating endoluminal ultrasound sources with expandable acoustic reflector and lens components — could be combined into different applicator configurations besides the end‐firing design evaluated herein. One alternative design that is also under development by our group constitutes a side‐firing applicator, which could be more appropriate for specific target sites along luminal passages. Furthermore, beyond a simple spherical convex profile, a fixed‐shape lens membrane could be molded to a custom shape or profile to create more complex beam patterns that are tailored for specific target sites or various thermal (i.e., ablation, hyperthermia) or mechanical (e.g., drug delivery) therapeutic applications.
5. Conclusions
Concepts and designs for integrating catheter‐based endoluminal ultrasound devices with deployable acoustic reflectors and fluid lenses, in order to enhance acoustic output and penetration depth from small diameter devices, have been introduced. Acoustic simulations that incorporate acoustic transmission and reflection at material interfaces were performed, and show good agreement with experimental characterization of a test applicator assembly. Parametric modeling studies demonstrate capability of the proposed applicator design to achieve high focal gain and localized ablative temperature elevation at target depths between 10–100 mm. Based upon these positive findings, future studies will be directed toward further theoretical analysis and construction of complete prototypes of the proposed applicator for experimental evaluations.
Acknowledgments
The work was supported in part by National Institutes of Health grant P01CA159992. This research was conducted with Government support under and awarded by DOD, Air Force Office of Scientific Research, National Defense Science and Engineering Graduate (NDSEG) Fellowship, 32 CFR 168a. The authors alone are responsible for the content and writing of the paper.
References
- 1. Salgaonkar VA, Diederich CJ. Catheter‐based ultrasound technology for image‐guided thermal therapy: current technology and applications. Int J Hyperthermia. 2015;31:203–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Kennedy JE. High‐intensity focused ultrasound in the treatment of solid tumours. Nat Rev Cancer. 2005;5:321–327. [DOI] [PubMed] [Google Scholar]
- 3. Melodelima D, Prat F, Fritsch J, Theillere Y, Cathignol D. Treatment of esophageal tumors using high intensity intraluminal ultrasound: first clinical results. J Transl Med. 2008;6:28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Pioche M, Lafon C, Constanciel E, et al. High‐intensity focused ultrasound liver destruction through the gastric wall under endoscopic ultrasound control: first experience in living pigs. Endoscopy. 2012;44:E376–E377. [DOI] [PubMed] [Google Scholar]
- 5. Melodelima D, Salomir R, Chapelon J, Theillère Y, Moonen C, Cathignol D. Intraluminal high intensity ultrasound treatment in the esophagus under fast MR temperature mapping: in vivo studies. Magn Reson Med. 2005;54:975–982. [DOI] [PubMed] [Google Scholar]
- 6. Li T, Khokhlova T, Maloney E, et al. Endoscopic high‐intensity focused US: technical aspects and studies in an in vivo porcine model (with video). Gastrointest Endosc. 2015;81:1243–1250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Adams MS, Salgaonkar VA, Plata‐Camargo J, et al. Endoluminal ultrasound applicators for MR‐guided thermal ablation of pancreatic tumors: preliminary design and evaluation in a porcine pancreas model. Med Phys. 2016;43:4184–4197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Chopra R, Colquhoun A, Burtnyk M, et al. MR imaging–controlled transurethral ultrasound therapy for conformal treatment of prostate tissue: initial feasibility in humans. Radiology. 2012;265:303–313. [DOI] [PubMed] [Google Scholar]
- 9. Chopra R, Burtnyk M, Haider MA, Bronskill MJ. Method for MRI‐guided conformal thermal therapy of prostate with planar transurethral ultrasound heating applicators. Phys Med Biol. 2005;50:4957. [DOI] [PubMed] [Google Scholar]
- 10. Diederich C, Stafford R, Nau W, Burdette E, Price R, Hazle J. Transurethral ultrasound applicators with directional heating patterns for prostate thermal therapy: in vivo evaluation using magnetic resonance thermometry. Med Phys. 2004;31:405–413. [DOI] [PubMed] [Google Scholar]
- 11. Sommer G, Pauly KB, Holbrook A, et al. Applicators for magnetic resonance‐guided ultrasonic ablation of benign prostatic hyperplasia. Invest Radiol. 2013;48:387–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Gelet A, Chapelon J, Bouvier R, et al. Transrectal high‐intensity focused ultrasound: minimally invasive therapy of localized prostate cancer. J Endourol. 2000;14:519–528. [DOI] [PubMed] [Google Scholar]
- 13. Chapelon J, Ribault M, Birer A, Vernier F, Souchon R, Gelet A. Treatment of localised prostate cancer with transrectal high intensity focused ultrasound. Eur J Ultrasound. 1999;9:31–38. [DOI] [PubMed] [Google Scholar]
- 14. Mabin T, Sapoval M, Cabane V, Stemmett J, Iyer M. First experience with endovascular ultrasound renal denervation for the treatment of resistant hypertension. EuroIntervention. 2012;8:57–61. [DOI] [PubMed] [Google Scholar]
- 15. Nakagawa H, Antz M, Wong T, et al. Initial experience using a forward directed, high‐intensity focused ultrasound balloon catheter for pulmonary vein antrum isolation in patients with atrial fibrillation. J Cardiovasc Electrophysiol. 2007;18:136–144. [DOI] [PubMed] [Google Scholar]
- 16. Sinelnikov Y, Fjield T, Sapozhnikov O. The mechanism of lesion formation by focused ultrasound ablation catheter for treatment of atrial fibrillation. Acoust Phys. 2009;55:647–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Wootton JH, Hsu IJ, Diederich CJ. Endocervical ultrasound applicator for integrated hyperthermia and HDR brachytherapy in the treatment of locally advanced cervical carcinoma. Med Phys. 2011;38:598–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Klingler HC, Susani M, Seip R, Mauermann J, Sanghvi N, Marberger MJ. A novel approach to energy ablative therapy of small renal tumours: laparoscopic high‐intensity focused ultrasound. Eur Urol. 2008;53:810–818. [DOI] [PubMed] [Google Scholar]
- 19. Hynynen K, Watmough D, Mallard J. Design of ultrasonic transducers for local hyperthermia. Ultrasound Med Biol. 1981;7:397–402. [DOI] [PubMed] [Google Scholar]
- 20. Yoon YJ, Benkeser PJ. Sound field calculations for an ultrasonic linear phased array with a spherical liquid lens. IEEE Trans Ultrason Ferroelectr Freq Control. 1992;39:268–272. [DOI] [PubMed] [Google Scholar]
- 21. Yoon YJ, Benkeser P. Ultrasonic phased arrays with variable geometric focusing for hyperthermia applications. IEEE Trans Ultrason Ferroelectr Freq Control. 1992;39:273–278. [DOI] [PubMed] [Google Scholar]
- 22. Ocheltree KB, Frizzel L. Sound field calculation for rectangular sources. IEEE Trans Ultrason Ferroelectr Freq Control. 1989;36:242–248. [DOI] [PubMed] [Google Scholar]
- 23. Fan X, Hynynen K. The effects of curved tissue layers on the power deposition patterns of therapeutic ultrasound beams. Med Phys. 1994;21:25–34. [DOI] [PubMed] [Google Scholar]
- 24. Moros EG, Fan X, Straube WL. Ultrasound power deposition model for the chest wall. Ultrasound Med Biol. 1999;25:1275–1287. [DOI] [PubMed] [Google Scholar]
- 25. O'Neil H. Theory of focusing radiators. J Acoust Soc Am. 1949;21:516–526. [Google Scholar]
- 26. Lee C, Benkeser PJ. A computationally efficient method for the calculation of the transient field of acoustic radiators. J Acoust Soc Am. 1994;96:545–551. [Google Scholar]
- 27. Bull V, ter Haar GR. The physics of ultrasound energy sources. In: Physics of Thermal Therapy: Fundamentals and Clinical Applications. Boca Raton, FL: Taylor & Francis; 2012:75–94. [Google Scholar]
- 28. Knollman G, Bellin J, Weaver J. Variable‐focus liquid‐filled hydroacoustic lens. J Acoust Soc Am. 1971;49:253–261. [Google Scholar]
- 29. Varadarajulu S, Banerjee S, Barth BA, et al. GI endoscopes. Gastrointest Endosc. 2011;74:1–6. e6. [DOI] [PubMed] [Google Scholar]
- 30. Francis A. Duck, Physical Properties of Tissues: A Comprehensive Reference Book. London: Anonymous Academic Press; 2013. [Google Scholar]
- 31. Stewart HF. Ultrasonic measurement techniques and equipment output level. In: Essentials of Medical Ultrasound. Clifton, New Jersey: Humana; 1982:77–116. [Google Scholar]
- 32. Pennes HH. Analysis of tissue and arterial blood temperatures in the resting human forearm. J Appl Physiol. 1948;1:93–122. [DOI] [PubMed] [Google Scholar]
- 33. Deardorff DL, Diederich CJ. Ultrasound applicators with internal water‐cooling for high‐powered interstitial thermal therapy. IEEE Trans Biomed Eng. 2000;47:1356–1365. [DOI] [PubMed] [Google Scholar]
- 34. Hasgall P, Neufeld E, Gosselin M, . IT'IS Database for thermal and electromagnetic parameters of biological tissues. Version 2.4, July 30th, 2013; 2013.
- 35. Adams MS, Scott SJ, Salgaonkar VA, Sommer G, Diederich CJ. Thermal therapy of pancreatic tumors using endoluminal ultrasound: parametric and patient‐specific modeling. Int J Hyperthermia. 2016;32:97–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Nylund K, Hausken T, Ødegaard S, Eide G, Gilja O. Gastrointestinal wall thickness measured with transabdominal ultrasonography and its relationship to demographic factors in healthy subjects. Ultraschall Med. 2012;33:E225. [DOI] [PubMed] [Google Scholar]
- 37. Prakash P, Diederich CJ. Considerations for theoretical modelling of thermal ablation with catheter‐based ultrasonic sources: implications for treatment planning, monitoring and control. Int J Hyperthermia. 2012;28:69–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Saab MA. Applications of high‐pressure balloons in the medical device industry. Medical Device & Diagnostic Industry Magazine, 86‐94; 2000.
- 39. Roche ET, Fabozzo A, Lee Y, et al. A light‐reflecting balloon catheter for atraumatic tissue defect repair. Sci Transl Med. 2015;7: 306ra149. [DOI] [PubMed] [Google Scholar]
- 40. Chipperfield FA, Dunkerton SA. Welding and joining techniques for polymeric medical devices. Welding Cutting. 2004;56:208–209. [Google Scholar]
- 41. Pullen D, Tavakoli S, Pullen D, Dunkerton S. A review of adhesive bonding techniques for joining medical materials. Assem Autom. 2005;25:100–105. [Google Scholar]


