Fig. 4. Performance of the code under different kinds of artificial errors.

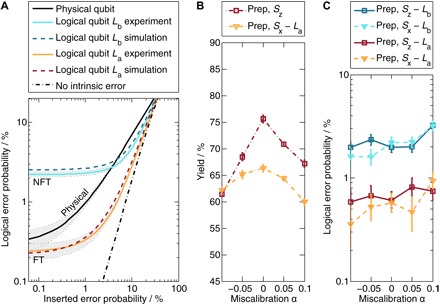
(A) Logical error probability under artificially introduced stochastic Pauli errors. Uncertainties shown in gray with dashed outlines. We prepare state |00〉_L, introduce a specific error, and apply S_z before readout. The parameter values for the curves (see Materials and Methods) corresponding to the two logical qubits are determined either experimentally (solid lines) or from simulation (dashed lines). The black curve shows the limiting theoretical case without intrinsic errors (see Materials and Methods). At low added error rates, the intrinsic errors dominate, and the fault-tolerantly constructed qubit L_a starts about an order of magnitude below the non–fault-tolerantly constructed qubit L_b. With increasing inserted error probability, the added Pauli errors become dominant, and the L_a/b curves converge and approach the theory curve without intrinsic error. The solid black line shows the error rate for a single physical qubit. L_a results in a lower error across the entire range relative to the physical qubit, although our measurement uncertainty means that this is no longer significant below p ~ 0.07%. The L_b error is lower than the physical qubit for added errors >4%. (B and C) Preparing |00〉_L and measuring S_x/z with purposefully miscalibrated two-qubit gates, known as XX-gates. A miscalibration of α means that the Bell state produced by the gate is imbalanced: $\sqrt{0.5-\mathrm{\alpha }}|00\rangle +\mathit{i}\sqrt{0.5+\mathrm{\alpha }}|11\rangle$. The yields diminishing with miscalibration for the stabilizer measurements are shown in (B), whereas the errors on the logical qubits presented in (C) remain similar, with L_a errors about an order of magnitude lower than L_b errors.