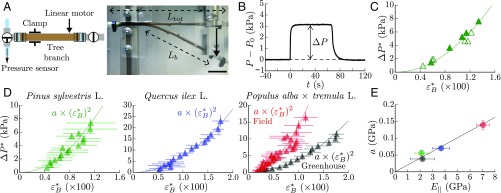
Fig. 4.

Hydraulic pulse induced by bending in natural tree branches. (A) Sketch of the experimental setup, where $L_{\text{tot}}$ is the total branch length and $L_b$ the bent length. (Scale bar, 5 cm.) (B) Xylem water pressure measured at the fixed extremity of a pine branch (Pinus sylvestris L.) in response to a bent/unbent sequence. (C) Relationship between the overpressure and the bending strain for the same branch using two different bending protocols: incremental step displacement (filled symbols) and step displacement with return to the initial position after each bending (open symbols). Here, $\mathrm{\Delta }{P}^{\ast }=\mathrm{\Delta }P\times (L_{\text{tot}}/L_b)$ and ${\epsilon }_B^{\ast }={\epsilon }_B{(1+{\epsilon }_B^0/{\epsilon }_B)}^{1/2}$, where ${\epsilon }_B=R(\overline{C}-{\overline{C}}^0)$ and ${\epsilon }_B^0=R{\overline{C}}^0$, with ${\overline{C}}^0$ the mean curvature of the branch at rest (Extension of the Model to Beams with a Rest Curvature). The solid line is a quadratic fit of the data. (D) Overpressure $\mathrm{\Delta }{P}^{\ast }$ vs. bending strain ${\epsilon }_B^{\ast }$ averaged over $n$ branches for different tree species and growing conditions (symbols) with quadratic fit $a\times {\epsilon }_B^{\ast 2}$ (solid lines). Green: P. sylvestris L., $n=6$, $a=0.056\pm 0.008$ GPa, $R^2=0.91$; blue: Q. ilex L., $n=5$, $a=0.070\pm 0.005$ GPa, $R^2=0.94$; red: Populus alba $\times$ tremula L. grown in field condition, $n=7$, $a=0.139\pm 0.013$ GPa, $R^2=0.88$; black: P. alba $\mathrm{\times }$ tremula L. grown in greenhouse conditions, $n=4$, $a=0.038\pm 0.003$ GPa, $R^2=0.98$). Each symbol corresponds to a running average over five data (seven data for poplar in field conditions) with an overlap of 50$\%$; error bars give the SD. (E) Coefficient of the quadratic fit $a$ as function of the longitudinal Young’s modulus $E_{\parallel }$ (same color as in D). The coefficient $a$ is found proportional to $E_{\parallel }$ (solid line: linear fit, $R^2=0.96$).