TESTING HIGH-DIMENSIONAL COVARIANCE MATRICES, WITH APPLICATION TO DETECTING SCHIZOPHRENIA RISK GENES

Abstract

Scientists routinely compare gene expression levels in cases versus controls in part to determine genes associated with a disease. Similarly, detecting case-control differences in co-expression among genes can be critical to understanding complex human diseases; however statistical methods have been limited by the high dimensional nature of this problem. In this paper, we construct a sparse-Leading-Eigenvalue-Driven (sLED) test for comparing two high-dimensional covariance matrices. By focusing on the spectrum of the differential matrix, sLED provides a novel perspective that accommodates what we assume to be common, namely sparse and weak signals in gene expression data, and it is closely related with Sparse Principal Component Analysis. We prove that sLED achieves full power asymptotically under mild assumptions, and simulation studies verify that it outperforms other existing procedures under many biologically plausible scenarios. Applying sLED to the largest gene-expression dataset obtained from post-mortem brain tissue from Schizophrenia patients and controls, we provide a novel list of genes implicated in Schizophrenia and reveal intriguing patterns in gene co-expression change for Schizophrenia subjects. We also illustrate that sLED can be generalized to compare other gene-gene “relationship” matrices that are of practical interest, such as the weighted adjacency matrices.

1. Introduction

High throughput technologies provide the capacity for measuring potentially interesting genetic features on the scale of tens of thousands. With the goal of understanding various complex human diseases, a widely used technique is gene differential expression analysis, which focuses on the marginal effect of each variant. Converging evidence has also revealed the importance of co-expression among genes, but analytical techniques are still underdeveloped. Improved methods in this domain will enhance our understanding of how complex disease affects the patterns of gene expression, shedding light on both the development of disease and its pathological consequences.

Schizophrenia (SCZ), a severe mental disorder with 0.7% lifetime risk (McGrath et al., 2008), is one of the complex human traits that has been known for decades to be highly heritable but whose genetic etiology and pathological consequences remain unclear. What has been repeatedly confirmed is that a large proportion of SCZ liability traces to polygenetic variation involving many hundreds of genes together, with each variant exerting a small impact (Purcell et al., 2014; International Schizophrenia Consortium et al., 2009). Despite the large expected number, only a small fraction of risk loci have been conclusively identified (Schizophrenia Working Group of the Psychiatric Genomics Consortium, 2014). This failure is due mainly to the limited signal strength of individual variants and under-powered mean-based association studies. Still, several biological processes, including synaptic mechanisms and glutamatergic neurotransmission, have been reported to be implicated in the risk for SCZ (Fromer et al., 2016). The observation that each genetic variant contributes only moderately to risk, and that each affected individual carries many risk variants, suggests that SCZ develops as a consequence of subtle alterations of both gene expression and co-expression, which requires development of statistical methods to describe the subtle, wide-spread co-expression differences.

Pioneering efforts have started in this direction. Very recently, the CommonMind Consortium (CMC) completed a large-scale RNA sequencing on dorsolateral prefrontal cortex from 279 control and 258 SCZ subjects, forming the largest brain gene expression data set on SCZ (Fromer et al., 2016). Analyses of these data by the CommonMind Consortium suggest that many genes show altered expression between case and control subjects, although the mean differences are small. By combining gene expression and co-expression patterns with results from genetic association studies, it appears that genetic association signals tend to cluster in certain sets of tightly co-expressed genes, so called co-expression modules (Zhang and Horvath, 2005). Still, the study of how gene co-expression patterns change from controls to SCZ subjects remains incomplete. Here, we address this problem using a hypothesis test that compares the gene-gene covariance matrices between control and SCZ samples, with integrated variable selection.

The problem of two-sample test for covariance matrices has been thoroughly studied in traditional multivariate analysis (Anderson et al., 1958), but becomes nontrivial once we enter the high-dimensional regime. Most of the previous high-dimensional covariance testing methods are motivated by either the L_∞-type distance between matrices where all entries are considered (Schott, 2007; Li and Chen, 2012), or the L_∞-type distance where only the largest deviation is utilized (Cai, Liu and Xia, 2013; Chang et al., 2016). These two strategies are designed for two extreme situations, respectively: when almost all genes exhibit some difference in co-expression patterns, or when there is one “leading” pair of genes whose co-expression pattern has an extraordinary deviation in two populations. However, the mechanism of SCZ is most likely to lie somewhere in between, where the difference may occur among hundreds of genes (compared to a total of ≈ 20,000 human genes), yet each deviation remains small. Some other existing approaches include using the trace of the covariance matrices (Srivastava and Yanagihara, 2010), using random matrix projections (Wu and Li, 2015), and using energy statistics to measure the distance between two populations (Székely and Rizzo, 2013). But none of these methods is designed for the scenario in which the signals are both sparse and weak.

In this paper, we propose a sparse-Leading-Eigenvalue-Driven (sLED) test. It provides a novel perspective for matrix comparisons by evaluating the spectrum of the differential matrix, defined as the difference between two covariance matrices. This provides greater power and insight for many biologically plausible models, including the situation where only a small cluster of genes has abnormalities in SCZ subjects, so that the differential matrix is supported on a small sub-block. The test statistic of sLED links naturally to the fruitful results in Sparse Principal Component Analysis (SPCA), which is widely used for unsupervised dimension reduction in the high-dimensional regime. Both theoretical and simulation results verify that sLED has superior power under sparse and weak signals. In addition, sLED can be generalized to compare other gene-gene “relationship” matrices, including the weighted adjacency matrices that are commonly used in gene clustering studies (Zhang and Horvath, 2005). Applying sLED to the CMC data sheds light on novel SCZ risk genes, and reveals intriguing patterns that are previously missed by the mean-based differential expression analysis.

For the rest of this paper, we motivate and propose sLED for testing two-sample covariance matrices in Section 2. We provide two algorithms to compute the test statistic, and establish theoretical guarantees on the asymptotic consistency. In Section 3, we conduct simulation studies and show that sLED has superior power to other existing two-sample covariance tests under many scenarios. In Section 4, we apply sLED to the CMC data. We detect a list of genes implicated in SCZ and reveal interesting patterns of gene co-expression changes. We also illustrate that sLED can be generalized to comparing weighted adjacency matrices. Section 5 concludes the paper and discusses the potential of applying sLED to other datasets. All proofs are included in the Supplement. An implementation of sLED is provided at https://github.com/lingxuez/sLED.

2. Methods

2.1. Background

Suppose $X_1,\cdots ,X_n\stackrel{i.i.d}{\sim }(0_p,{\sum }_1)$ and $Y_1,\cdots ,Y_m\stackrel{i.i.d}{\sim }(0_p,{\sum }_2)$ are independent p-dimensional random variables coming from two populations with potentially different covariance structures. Without loss of generality, both expectations are assumed to be zero, and let D = Σ₂−Σ₁ be the differential matrix. The goal is to test

$$H_0:D=0\text{versus}{H}_1:D\ne 0.$$ (2.1)

This two-sample covariance testing problem has been well studied in the traditional “large n, small p” setting, where the likelihood ratio test (LRT) is commonly used. However, testing covariance matrices under the high-dimensional regime is a nontrivial problem. In particular, LRT is no longer well defined when p > min{n, m}. Even if p ≤ min {n, m}, LRT has been shown to perform poorly when p/min{n, m} → c ∈ (0, 1) Bai et al., 2009).

Researchers have approached this problem in different ways. Here, we review two of the main strategies to motivate our test. The first one starts from rewriting (2.1) as

$$H_0:{\Vert D\Vert }_F^2=0\text{versus}{H}_1:{\Vert D\Vert }_F^2\ne 0,$$ (2.2)

where ‖D‖_F is the Frobenius norm of D. This strategy includes a test statistic based on an estimator of ${\Vert D\Vert }_F^2$ under normality assumptions (Schott, 2007), as well as a test under more general settings using a linear combination of three U-statistics, which is also motivated by ${\Vert D\Vert }_F^2$ (Li and Chen, 2012). These L₂-based tests target a dense alternative, but usually suffer from loss of power when D has only a small number of non-zero entries.

On the other hand, Cai, Liu and Xia (2013) consider the sparse alternative, and rewrite (2.1) as

$$H_0:{\Vert D\Vert }_{\infty }=0\text{versus}{H}_1:{\Vert D\Vert }_{\infty }\ne 0,$$ (2.3)

where ‖D‖_∞ = max_i,j |D_ij|. Then the test statistic is constructed using a normalized estimator of ‖D‖_∞. Later, Chang et al. (2016) proposed a bootstrap procedure using the same test statistic but under weaker assumptions, and Cai and Zhang (2015) extended the idea to comparing two-sample correlation matrices. These L_∞-norm based tests have been shown to enjoy superior power when the single-entry signal is strong, in the sense that max_i,j |D_ij| is of order $\sqrt{\text{log}p/min\left\{n,m\right\}}$ or larger.

In this paper, we focus on the unexplored but practically interesting regime where the signal is both sparse and weak, meaning that the difference may occur at only a small set of entries, while the magnitude tends to be small. We propose another perspective to construct the test statistic by looking at the singular value of D, which is especially suitable for this purpose. To illustrate the idea, consider a toy example where

$$D_{ij}=\{\begin{array}{c}\rho ,1\le i,j\le s\\ 0,\text{otherwise}\end{array}$$ (2.4)

for some ρ > 0 and integer s ≪ p. In other words, Σ₂ and Σ₁ differ by ρ in only an s × s sub-block. In this case, the L₂-type tests are sub-optimal because they include errors from all entries; so are the L_∞-type tests because they utilize only one single entry ρ. On the other hand, the largest singular value of D is sρ, which extracts stronger signals with much less noise and therefore has the potential to gain more power.

More formally, we rewrite the testing problem (2.1) to be

$$H_0:{\sigma }_1\left(D\right)=0\text{versus}{H}_1:{\sigma }_1\left(D\right)\ne 0,$$ (2.5)

where σ₁(·) denotes the largest singular value. Compared to (2.2) and (2.3), (2.5) provides a novel perspective to study the two-sample covariance testing problem based on the spectrum of the differential matrix D, and will be the starting point of constructing our test statistic.

Notation

For a vector $v\in {\mathrm{ℝ}}^p$, let ${\Vert v\Vert }_q={\left({\displaystyle {\sum }_{i=1}^p{\left|v_i\right|}^q}\right)}^{1/q}$ be the L_q norm for q > 0, and ‖v‖₀ be the number of non-zero elements. For a symmetric matrix $A\in {\mathrm{ℝ}}^{p\times p}$, let A_ij be the (i, j)-th element, ‖A‖_q be the L_q norm of vectorized A, and tr(A) be the trace. In addition, we use λ₁(A) ≥ ⋯ ≥ λ_p(A) to denote the eigenvalues of A. For two symmetric matrices $A,B\in {\mathrm{ℝ}}^{p\times p}$, we write A⪰B when A−B real is positive semidefinite. Finally, for two sequences of numbers {x_n} and {y_n}, we write x_n = O(y_n) if |x_n/y_n| ≤ C for all n and some positive constant C, and x_n = o(y_n) if lim_n x_n/y_n = 0.

2.2. A two-sample covariance test: sLED

Starting from (2.5), note that

$${\sigma }_1\left(D\right)=max\left\{\left|{\lambda }_1\left(D\right)\right|,\left|{\lambda }_1\left(-D\right)\right|\right\}.$$

Therefore, a naive test statistic would be $T^{\text{naive}}=max\left\{\left|{\lambda }_1\left(\widehat{D}\right)\right|,\left|{\lambda }_1\left(-\widehat{D}\right)\right|\right\}$ for some estimator $\widehat{D}$. A simple estimator is the difference between the sample covariance matrices:

$$\widehat{D}={\widehat{\sum }}_2-{\widehat{\sum }}_1,\text{where}{\widehat{\sum }}_1=\frac{1}{n}{\displaystyle \sum _{k=1}^n{X}_k{X}_k^T},{\widehat{\sum }}_2=\frac{1}{m}{\displaystyle \sum _{l=1}^m{Y}_l{Y}_l^T}.$$ (2.6)

However, in the high-dimensional setting, ${\lambda }_1\left(\widehat{D}\right)$ is not necessarily a consistent estimator of λ₁(D), and without extra assumptions, there is almost no hope of reliable recovery of the eigenvectors (Johnstone and Lu, 2009). A popular remedy for this curse of dimensionality in many high-dimensional methods is to add sparsity assumptions, such as imposing an L₀ constraint on an optimization procedure. Note that for any symmetric matrix $A\in {\mathrm{ℝ}}^{p\times p}$,

$${\lambda }_1\left(A\right)=\underset{{\Vert v\Vert }_2=1}{max}{v}^{T}Av=\underset{{\Vert v\Vert }_2=1}{max}\text{tr}\left(A\left(v{v}^T\right)\right).$$

Following the common strategy, we consider the constrained problem:

$${\lambda }_1^R\left(A\right)=\underset{{\Vert v\Vert }_2=1,{\Vert v\Vert }_0\le R}{max}\text{tr}\left(A\left(v{v}^T\right)\right),$$ (2.7)

where R > 0 is some constant that controls the sparsity of the solution, and ${\lambda }_1^R\left(A\right)$ is usually referred to as the R-sparse leading eigenvalue of A. Then, naturally, we construct the following test statistic

$$T_R=max\left\{\left|{\lambda }_1^R\left(\widehat{D}\right)\right|,\left|{\lambda }_1^R\left(-\widehat{D}\right)\right|\right\},$$ (2.8)

and the sparse-Leading-Eigenvalue-Driven (sLED) test is obtained by thresholding T_R at the proper level.

Problem (2.7) is closely related with Sparse Principal Component Analysis (SPCA). The only difference is that in SPCA, the input matrix A is usually the sample covariance matrix, but here, we use the differential matrix $\widehat{D}$. Solving (2.7) directly is computationally intractable, but we will show in Section 2.3 that approximate solutions can be obtained.

Finally, because it is difficult to obtain the limiting distribution of T_R, we use a permutation procedure. Specifically, for any α ∈ (0, 1), the α−level sLED test, denoted by ${\mathrm{\Psi }}_{\mathit{sLED}}^{(\alpha )}$, is conducted as follows:

1. Given samples Z = (X₁, ⋯, X_n, Y₁,·⋯, Y_m), calculate the test statistic T_R as in (2.8).

2. Sample uniformly from Z without replacement to get $Z^{\ast }=\left(Z_1^{\ast },\cdots ,Z_N^{\ast }\right)$, where N = n + m. Calculate the permutation differential matrix ${\widehat{D}}^{\ast }$:

   $${\widehat{D}}^{\ast }={\widehat{\sum }}_2^{\ast }-{\widehat{\sum }}_1^{\ast },$$ (2.9)

   where ${\widehat{\sum }}_1^{\ast }=\frac{1}{n}{\displaystyle {\sum }_{k=1}^n{Z}_k^{\ast }{\left(Z_k^{\ast }\right)}^T}$, ${\widehat{\sum }}_2^{\ast }=\frac{1}{m}{\displaystyle {\sum }_{l=n+1}^N{Z}_l^{\ast }{\left(Z_l^{\ast }\right)}^T}$. That is, randomly permute the indices {1, ⋯, N}, treat the first n indices as from the first population and the·last m indices as from the second population.
3. Compute the permutation test statistic

   $$T_R^{\ast }=max\left\{\left|{\lambda }_1^R\left({\widehat{D}}^{\ast }\right)\right|,\left|{\lambda }_1^R\left(-{\widehat{D}}^{\ast }\right)\right|\right\}.$$ (2.10)
4. Repeat steps 2 – 3 for B times to get $T_R^{\ast \left(1\right)},\cdots ,T_R^{\ast \left(B\right)}$, then

   $$\widehat{p}=\frac{1}{B}{\displaystyle \sum _{b=1}^B{I}_{\{T_R^{\ast \left(b\right)}>T_R\}}},$$

   and sLED rejects H₀ if $\widehat{p}<\alpha$, i.e., ${\mathrm{\Psi }}_{\mathit{slED}}^{(\alpha )}=I_{\left\{\widehat{p}<\alpha \right\}}$.

Remark 1

We can also estimate the support of the R-sparse leading eigenvector of D, which provides a list of genes that are potentially involved in the disease. Without loss of generality, suppose ${\lambda }_1^R\left(\widehat{D}\right)>{\lambda }_1^R\left(-\widehat{D}\right)$, we define

$$\text{Leverage}:=\text{diag}\left(\widehat{v}{\widehat{v}}^T\right)={\left({\widehat{v}}_1^2,\cdots ,{\widehat{v}}_p^2\right)}^T,$$ (2.11)

where $\widehat{v}$ is the R-sparse leading eigenvector of $\widehat{D}$ in (2.7). Then the elements with large leverage will be the candidate genes that have altered covariance structure between the two populations.

2.3. Sparse principal component analysis

Many studies on Sparse Principal Component Analysis (SPCA) have provided various algorithms to approximate (2.7) when A is the sample covariance matrix. Most techniques utilize an L₁ constraint to achieve both sparsity and computational efficiency. To name a few, Jolliffe, Trendafilov and Uddin (2003) form the SCoT-LASS problem by directly replacing the L₀ constraint by L₁ constraint; Zou, Hastie and Tibshirani (2006) analyze the problem from a penalized regression perspective; Witten, Tibshirani and Hastie (2009) and Shen and Huang (2008) use the framework of low rank matrix completion and approximation; d’Aspremont et al. (2007) and Vu et al. (2013) consider the convex relaxation of (2.7). Recent development of atomic norms also provides an alternative approach to deal with the L₀ constrained problems (for example, see Oymak et al. (2015)). For the purpose of this paper, we give details of only the following two SPCA algorithms that can be directly generalized to approximate (2.7) with input matrix $\widehat{D}$, the differential matrix.

Fantope projection and selection (FPS)

For a symmetric matrix $A\in {\mathrm{ℝ}}^{p\times p}$, FPS (Vu et al., 2013) considers a convex optimization problem:

$${\lambda }_{\mathit{fps}}^R\left(A\right)=\underset{H\in {ℱ}^1,{\Vert H\Vert }_1\le R}{max}\text{tr}\left(AH\right),$$ (2.12)

where ℱ¹ = {H ∈ ℝ^p×p: symmetric, 0 ⪯ H ⪯ I, tr(H) = 1} is the 1-dimensional Fantope, which is the convex hull of all 1-dimensional projection matrices {vv^T: ‖v‖₂ = 1}. In addition, by the Cauchy-Schwarz inequality, if ‖v‖₂=1, then ‖vv^T‖₁ ≤ ‖v‖₀ Therefore, (2.12) is a convex (relaxation) of (2.7). Moreover, when the input matrix is $\widehat{D}$, the problem is still convex, and the ADMM algorithm proposed in Vu et al. (2013) can be directly applied. This algorithm has guaranteed convergence, but requires iteratively performing SVD on a p×p matrix. Moreover, the calculation needs to be repeated B times in the permutation procedure, and becomes computationally demanding when p is on the order of a few thousands. Therefore, we present an alternative heuristic algorithm below, which is much more efficient and typically works well in practice.

Penalized matrix decomposition (PMD)

For a general matrix $A\in {\mathrm{ℝ}}^{p\times p}$, PMD (Witten, Tibshirani and Hastie, 2009) solves a rank-one matrix completion problem:

$${\lambda }_{\mathit{pmd}}^R\left(A\right)=\underset{u,v}{max}\text{tr}\left(A\left(u{v}^T\right)\right),\text{subject to}{\Vert u\Vert }_2\le 1,{\Vert v\Vert }_2\le 1{\Vert u\Vert }_1\le \sqrt{R},{\Vert v\Vert }_1\le \sqrt{R}.$$ (2.13)

The solution for each one of u and v has a simple closed form after fixing the other one. This leads to a straightforward iterative algorithm, which has been implemented in the R package PMA. Moreover, if the solutions satisfy $\widehat{u}=\widehat{v}$, then they are also the solutions to the following non-convex Constrained-PMD problem:

$${\lambda }_{c-\mathit{pmd}}^R\left(A\right)=\underset{{\Vert v\Vert }_2\le 1,{\Vert v\Vert }_1\le \sqrt{R}}{max}\text{tr}\left(A\left(v{v}^T\right)\right).$$ (2.14)

Note that the solutions of (2.14) always have ‖v‖₂=1 which implies ${\Vert v\Vert }_1^2={\Vert v{v}^T\Vert }_1\le {\Vert v\Vert }_0$,so (2.14) is also an approximation to (2.7). Now observe that when A ⪰ 0, as in the usual SPCA setting, the solutions of (2.13) automatically have $\widehat{u}=\widehat{v}$ by the Cauchy-Schwarz inequality. However, this is no longer true when A is not positive semidefinite, as when we deal with the differential matrix $\widehat{D}$. To overcome this issue, we choose some constant d > 0 that is large enough such that A + dI ⪰ 0. Then the solutions of ${\lambda }_{\mathit{pmd}}^R\left(A+dI\right)$ will satisfy $\widehat{u}=\widehat{v}$, and it is easy to obtain ${\lambda }_{c-\mathit{pmd}}^R\left(A\right)$ by

$${\lambda }_{c-\mathit{pmd}}^R\left(A\right)={\lambda }_{\mathit{pmd}}^R\left(A+dI\right)-d.$$ (2.15)

2.4. Consistency

Finally, we show that sLED is asymptotically consistent. The validity of its size is guaranteed by the permutation procedure. Here, we prove that sLED also achieves full power asymptotically, under the following assumptions:

• (A1)(Balanced sample sizes) $\underset{\_}{c}n\le m\le \overline{c}n$ for some constants $0<\underset{\_}{c}\le 1\le \overline{c}<\infty$.
• (A2)
  (Sub-gaussian tail) Let (Z₁, ⋯, Z_N) = (X₁, ⋯, X_n, Y₁, ⋯, Y_m), then every Z_k is sub-gaussian with parameter ν², that is,

  $$\mathbb{E}\left[e^{t\left(Z_k^{T}u\right)}\right]\le e^{\frac{t^2{\nu }^2}{2}},\forall t>0,\forall u\in {\mathrm{ℝ}}^p\text{such}\text{that}{\Vert u\Vert }_2=1.$$
• (A3)(Dimensionality) (log p)³ = O(n).
• (A4)
  (Signal strength) Under H₁, for some constant C to be specified later,

  $$max\left\{{\lambda }_1^R\left(D\right),{\lambda }_1^R\left(-D\right)\right\}\ge CR\sqrt{\frac{\text{log}p}{n}}.$$

Theorem 1 (Power of sLED)

Let T_R be the test statistic as defined in (2.8), and $T_R^{\ast }$ be the permutation test statistic as defined in (2.10), where ${\lambda }_1^R(\cdot )$ is approximated by the L₁ constrained algorithms (2.12) or (2.14). Then under assumptions (A1)–(A3), for ∀δ > 0, there exists a constant C depending on $\left(\underset{\_}{c},\overline{c},{\nu }^2,\delta \right)$, such that if assumption (A4) holds, and n, p are sufficiently large,

$${\mathbb{P}}_{H_1}\left(T_R({\widehat{D}}^{\ast })>T_R(\widehat{D})\right)\le \delta .$$

As a consequence, for any pre-specified level α ∈ (0, 1), pick δ = α/2, then

$${\mathbb{P}}_{H_1}\left({\mathrm{\Psi }}_{\mathit{sLED}}^{\left(\alpha \right)}=1\right)\to 1asB\to +\infty .$$

The proof of Theorem 1 contains two steps. First, Theorem 2 provides an upper bound of the entries in ${\widehat{D}}^{\ast }$. Then Theorem 3 ensures that the permutation test statistic $T_R^{\ast }$ is controlled by $\Vert {\widehat{D}}^{\ast }\Vert \infty$, and the test statistic T_R is lower-bounded in terms of the signal strength. We state Theorem 2 and Theorem 3 below, and the proof details are included in the Supplement.

Theorem 2 (Permutation differential matrix)

Under assumptions (A1)–(A3), let ${\widehat{D}}^{\ast }$ be the permutation differential matrix as defined in (2.9), then ∀δ > 0, there exist constants C, C₁ depending on $\left({\nu }^2,\underset{\_}{c},\overline{c}\right)$, such that if n, p are sufficiently large,

$$\mathbb{P}\left({\Vert {\widehat{D}}^{\ast }\Vert }_{\infty }>C\sqrt{\frac{\text{log}\left(C_1{p}^2/\delta \right)}{n}}\right)\le \delta .$$

Theorem 3 (Test statistic)

For any symmetric matrix $\widehat{D}$, let ${\stackrel{\sim }{\lambda }}_1^R\left(\widehat{D}\right)$ be a solution of the L₁ constrained algorithms (2.12) or (2.14), then the following statements hold:

1. If ${\Vert \widehat{D}\Vert }_{\infty }\le \epsilon$ for some ε > 0, then ${\stackrel{\sim }{\lambda }}_1^R\left(\widehat{D}\right)\ge R\epsilon$.

2. If there is a matrix D such that ${\Vert \widehat{D}-D\Vert }_{\infty }\le \epsilon$ for some ε > 0, then

   $${\stackrel{\sim }{\lambda }}_1^R\left(\widehat{D}\right)\ge {\lambda }_1^R\left(D\right)-R\epsilon .$$

Remark 2

Assumption (A4) does not require the leading eigenvector of D (or −D) to be sparse, only that the sparse signal be strong enough, which is a very mild requirement.

Remark 3

Theorems 1–3 suggest that sLED is as powerful as the maximum entry test by Cai, Liu and Xia (2013). Consider the toy example in (2.4) and L₁ radius R = s. Assumption (A4) for the L₁ constrained problem implies that sLED is powerful if $\rho \ge C\sqrt{\text{log}p/n}$, which is the same rate required for the maximal entry test. When the signal strength ρ is below the rate of $\sqrt{\text{log}p/n}$, the maximal entry test has no power. A related result in sparse PCA due to Berthet and Rigollet (2013) implies that sLED is unlikely to be powerful in this case either.

2.5. Choosing sparsity parameter R

The tuning parameter R in (2.12) and (2.14) plays an important role in sLED test. If R is too large, the method uses little regularization and assumption (A4) is unlikely to hold. If R is too small, then the constraint is too strong to cover the signal in the differential matrix. The practical success of sLED requires an appropriate choice of R. We know that R provides a natural, but possibly loose, lower bound on the support size of the estimated sparse eigenvector. In general, one can use cross-validation to choose R, so that the estimated leading sparse singular vector maximizes its inner product with a differential matrix computed from a testing subsample.

In applications, one can often choose R with the aid of subject background knowledge and the context of subsequent analysis. For example, in the detection of Schizophrenia risk genes, we typically expect to report a certain proportion in a collection of genes for further investigation. Thus one can choose from a set of candidate values of R to match the desired number of discoveries. In this paper, following Witten, Tibshirani and Hastie (2009), we use algorithm (2.14) and choose the sparsity parameter R to be

$$\sqrt{R}=c\sqrt{p}\text{for}\text{some}c\in \left(0,1\right),$$ (2.16)

then c² provides a loose lower bound on the proportion of selected genes. We will illustrate in simulation studies (Section 3) and the CMC data application (Section 4) that sLED is stable with a reasonable range of c.

3. Simulations

In this section, we conduct simulation studies to compare the power of sLED with other existing methods: Schott (2007) use an estimator of the Frobenius norm ${\Vert D\Vert }_F^2$ (Sfrob); Li and Chen (2012) use a linear combination of three U-statistics which is also motivated by ${\Vert D\Vert }_F^2$ (Ustat); Cai, Liu and Xia (2013) use the maximal absolute entry of D (Max); Chang et al. (2016) use a multiplier bootstrap on the same test statistic (MBoot), and Wu and Li (2015) use random matrix projections (RProj). To obtain a fair comparison of empirical power, we use permutation to compute the p-values for all methods, except for MBoot, which already uses a bootstrap procedure. Here, we focus on comparing the empirical power in the rest of this section. The empirical sizes are reported in the supplement. The simulation results in this section can be reproduced using the code provided at https://github.com/lingxuez/sLED.

We consider four different covariance structures of Σ₁ and Σ₂ = Σ₁ + D under the alternative hypothesis. Under each scenario i = 1, ⋯, 4, we first generate a base matrix Σ^∗(i), and we enforce positive definiteness using Σ₁ = Σ^∗(i)+δI_p and Σ₁ = Σ^∗(i)+D+δI_p, where δ = |min{λ_min(Σ^∗(i)), λ_min(Σ^∗(i) + D)}| + 0.05. Now we specify the structures of {Σ^∗(i)}_i=1,…,4. Under each scenario, we let $\mathrm{\Lambda }\in {\mathrm{ℝ}}^{p\times p}$ to be a diagonal matrix with diagonal elements being sampled from Unif(0.5, 2.5) independently. We denote ⌊x⌋ to be the largest integer that is smaller than or equal to x.

1. Noisy diagonal. Let ${\mathrm{\Delta }}_{ii}^{\left(1\right)}=1$, ${\mathrm{\Delta }}_{ij}^{\left(1\right)}\sim \text{Bernoulli}(0.05)$ when i < j, and ${\mathrm{\Delta }}_{ij}^{\left(1\right)}={\mathrm{\Delta }}_{ji}^{\left(1\right)}$ when i > j for symmetry, and we define Σ^∗(1) = Λ^1/2Δ⁽¹⁾Λ^1/2. This model is also considered in Cai, Liu and Xia (2013).

2. Block diagonal. Let K = ⌊p/10⌋ be the number of blocks, ${\mathrm{\Delta }}_{ii}^{\left(2\right)}=1$, ${\mathrm{\Delta }}_{ij}^{\left(2\right)}=0.55$ when 10(k − 1) + 1 ≤ i ≠ j ≤ 10k for k 1, ⋯, K, and zero otherwise. We define Σ^∗(2) = Λ^1/2Δ⁽²⁾Λ^1/2. This model is also considered in Cai, Liu and Xia (2013) and Chang et al. (2016).

3. Exponential decay. Let ${\mathrm{\Delta }}_{ij}^{\left(3\right)}={0.5}^{\left|i-j\right|}$, and Σ^∗(3) = Λ^1/2Δ⁽³⁾Λ^1/2. This model is also considered in Cai, Liu and Xia (2013) and Chang et al. (2016).

4. WGCNA. Finally, Σ^∗(4) is computed based on the CMC data (Fromer et al., 2016) using the simulation tool provided by WGCNA (Zhang and Horvath, 2005). Specifically, we first compute the eigengene (i.e., the first principal component) of the M2c module for the 279 control samples. The M2c module will be the focus of Section 4, and more detailed discussion is provided there. We use the simulateDatExpr command in the WGCNA R package to simulate new expressions for p genes of the 279 samples. We set modProportions=(.8,.2), such that 80% of the p genes are simulated to be correlated with the M2c eigengene, and the other 20% genes are randomly generated. Default values are used for all other parameters. Finally, Σ^∗(4) is set to be the sample covariance matrix.

We consider the following two types of differential matrix D:

1. Sparse block difference. Suppose D is supported on an s × s sub-block with s = ⌊0.1p⌋, and the non-zero entries are generated from Unif(d/2, 2d) independently. The signal level d is chosen to be $d=\frac{1}{2}\sqrt{\left({max}_{1\le j\le p}{\sum }_{jj}^{\ast }\right)\text{log}\left(p\right)}$ where Σ^∗ is the base matrix defined above.

2. Soft-sparse spiked difference. Let D be a rank-one matrix with D = dvv^T, where v is a soft-sparse unit vector with ‖v‖₂=1 and ║v║₀ = ⌊0.2p⌋. The support of v is uniformly sampled from {1, ⋯, p} without replacement. Among the non-zero elements, ⌊0.1p⌋ are·sampled from N(1, 0.01), and the remaining ⌊0.2p⌋−⌊0.1p⌋ are sampled from N(0.1, 0.01). Finally, v is normalized to have unit L₂ norm. The signal level d is set to be $d=4\sqrt{{max}_{1\le j\le p}{\sum }_{jj}^{\ast }\text{log}(p)}$, where Σ^∗ is the base matrix defined above. The differential matrix D under this scenario is moderately sparse, with ⌊0.1p⌋ features exerting larger signals.

Finally, the samples are generated by $X_i={\sum }_1^{1/2}{Z}_i$ for i = 1, ⋯, n, and $Y_l={\sum }_2^{1/2}{Z}_{n+l}$ for l = 1, ⋯, m, where {Z_i}_i=1,n+m are independent p-dimensional random variables with i.i.d. coordinates Z_ij, j = 1, ⋯, p. We consider the following four distributions for Z_ij:

1. Standard Normal N(0, 1).

2. Centralized Gamma distribution with α = 4, β = 0.5 (i.e., the theoretical expectation αβ = 2 is subtracted from Γ(4, 0.5) samples). This distribution is also considered in Li and Chen (2012) and Cai, Liu and Xia (2013).

3. t-distribution with degrees of freedom 12. This distribution is also considered in Cai, Liu and Xia (2013) and Chang et al. (2016).

4. Centralized Negative Binomial distribution with mean μ = 2 and dispersion parameter ϕ = 2 (i.e., the theoretical expectation μ = 2 is subtracted from NB(2, 2) samples).

Note that when Z_ij ~ N(0, 1), X and Y are multinomial Gaussian random variables with covariance matrices Σ₁ and Σ₂. We also consider three non-Gaussian distributions to account for the heavy-tail scenario observed in many genetic data sets.

Here, the smoothing parameter for sLED is set to be $\sqrt{R}=0.3\sqrt{p}$, and 100 random projections are used for Rproj. For sLED, Max, Ustat, Sfrob, and Rproj, 100 permutations are used to obtain each p-value; for MBoot, 100 bootstrap repetitions are used. Table 1 summarizes the empirical power under different covariance structures and differential matrices when Z_ij’s are sampled from standard Normal and centralized Gamma distribution. We see that sLED is more powerful than many existing methods under most scenarios. The results using the other two distributions of Z have similar patterns, and due to space limitation we include them in the Supplement.

Table 1.

Empirical power in 100 repetitions, where n = m = 100, nominal level α = 0.05, and Z_ij’s are sampled from standard normal (top) and centralized Gamma (4, 0.5) (bottom). Under each scenario, the largest power is highlighted.

D	Σ1	Noisy diagonal			Block diagonal			Exp. decay			WGCNA
	p	100	200	500	100	200	500	100	200	500	100	200	500
Gaussian
Block	Max	0.38	0.14	0.11	0.94	0.54	0.25	0.98	0.86	0.31	0.92	0.64	0.16
	MBoot	0.39	0.18	0.13	0.94	0.54	0.31	0.98	0.88	0.30	0.89	0.63	0.20
	Ustat	0.71	0.66	0.74	0.98	0.96	0.95	1.00	1.00	0.99	0.76	0.78	0.85
	Sfrob	0.72	0.64	0.73	0.97	0.95	0.95	1.00	1.00	0.99	0.72	0.79	0.86
	RProj	0.09	0.13	0.09	0.13	0.16	0.14	0.24	0.16	0.09	0.20	0.17	0.06
	sLED	1.00	0.99	1.00	1.00	0.99	1.00	1.00	1.00	1.00	0.98	0.96	0.95
Spiked	Max	0.12	0.08	0.05	0.49	0.26	0.09	0.96	0.90	0.15	0.86	0.32	0.04
	MBoot	0.12	0.08	0.05	0.51	0.29	0.11	0.98	0.90	0.17	0.79	0.31	0.07
	Ustat	0.20	0.11	0.13	0.76	0.44	0.06	1.00	0.95	0.60	0.30	0.10	0.04
	Sfrob	0.18	0.12	0.11	0.73	0.41	0.07	1.00	0.93	0.62	0.34	0.14	0.03
	RProj	0.10	0.08	0.02	0.32	0.08	0.12	0.30	0.20	0.09	0.61	0.24	0.13
	sLED	0.51	0.11	0.03	0.97	0.701	0.12	1.00	1.00	1.00	0.97	0.57	0.05
Centralized Gamma
Block	Max	0.42	0.20	0.14	0.89	0.71	0.28	0.96	0.82	0.42	0.77	0.67	0.27
	MBoot	0.42	0.14	0.10	0.86	0.58	0.20	0.95	0.77	0.33	0.72	0.63	0.25
	Ustat	0.57	0.59	0.70	0.92	0.94	0.97	0.99	0.98	0.98	0.53	0.82	0.86
	Sfrob	0.58	0.55	0.71	0.92	0.92	0.98	0.99	0.99	0.98	0.50	0.76	0.81
	RProj	0.11	0.10	0.09	0.24	0.17	0.16	0.41	0.15	0.14	0.21	0.07	0.14
	sLED	0.96	0.98	0.99	0.99	1.00	1.00	1.00	1.00	1.00	0.94	0.88	0.94
Spiked	Max	0.08	0.09	0.03	0.72	0.39	0.05	0.99	0.71	0.22	0.91	0.35	0.04
	MBoot	0.10	0.07	0.02	0.74	0.36	0.09	0.99	0.71	0.16	0.88	0.35	0.04
	Ustat	0.32	0.08	0.11	0.78	0.41	0.07	1.00	0.94	0.70	0.33	0.08	0.05
	Sfrob	0.34	0.07	0.10	0.80	0.37	0.07	1.00	0.96	0.74	0.28	0.04	0.04
	RProj	0.12	0.06	0.07	0.32	0.12	0.06	0.36	0.14	0.10	0.63	0.22	0.10
	sLED	0.56	0.14	0.05	0.97	0.71	0.14	1.00	1.00	1.00	0.93	0.51	0.08

Finally, we examine the sensitivity of sLED to the smoothing parameter. Recall that the smoothing parameter is set to be $\sqrt{R}=c\sqrt{p}$ as explained in Section 2.5. Figure 1 visualizes the empirical power of sLED using c ∈ {0.10, 0.12, ⋯, 0.30} when D has sparse block difference and Z_ij’s are sampled from N(0, 1). It is clear that sLED remains powerful for a wide range of c. Similar patterns are observed under other scenarios, and we include these results in the Supplement.

Fig. 1.

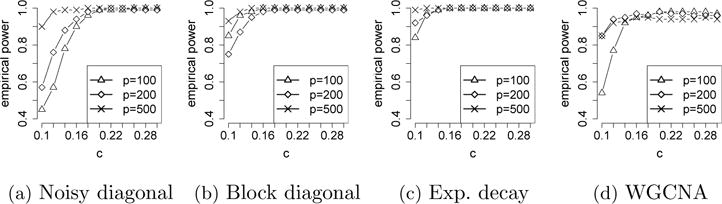
Empirical power of sLED in 100 repetitions using different smoothing parameters $\sqrt{R}=c\sqrt{p}$ for c ∈ {0.10, ⋯, 0.30}, where D has sparse block difference and Z_ij’s are from sampled N(0, 1).

4. Application to Schizophrenia data

In this section, we apply sLED to the CommonMind Consortium (CMC) data, containing RNA-sequencing on 16,423 genes from 258 Schizophrenia (SCZ) subjects and 279 control samples (Fromer et al., 2016). The RNA-seq data has been carefully processed, including log-transformation and adjustment of various covariates using a weighted linear regression. The CMC group further cluster the genes into 35 genetic modules using the WGCNA tool (Zhang and Horvath, 2005), such that genes within each module tend to be closely connected and have related biological functionalities. Among these, the M2c module, containing 1,411 genes, is the only one that is enriched with genes exhibiting differential expression and with prior genetic associations with schizophrenia (SCZ). We direct readers to the original paper (Fromer et al., 2016) for more detailed description of the data processing and genetic module analysis. In the rest of this section, we apply sLED to investigate the co-expression differences between cases and controls in the M2c module, which is of the greatest scientific interest. We center and standardize the expression data, such that each gene has mean 0 and standard deviation 1 across samples. Therefore, the covariance test is applied to correlation matrices.

4.1. Testing co-expression differences

In this section, we use sLED to compare the correlation matrices among the 1,411 M2c-module genes between SCZ and control samples. The sparsity parameter in (2.14) is chosen to be $\sqrt{R}=c\sqrt{p}$, and as explained in Section 2.5, c² provides a loose lower bound on the proportion of selected genes. Here, because the number of risk genes that carry the genetic signals is expected to be roughly in the range of 1%–10%, we choose c = 0.1. Applying sLED with 1,000 permutation repetitions, we obtain a p-value of 0.014, indicating a significant difference between SCZ and control samples.

We then identify the key genes that drive this difference according to their leverage, as defined in (2.11). Specifically, we order the leverage of all genes, such that ${\widehat{v}}_{\left(1\right)}^2\ge {\widehat{v}}_{\left(2\right)}^2\ge \cdots \ge {\widehat{v}}_{\left(p\right)}^2$, where larger leverage usually indicates stronger signals. Note that by construction, ${\displaystyle {\sum }_{i=1}^p{\widehat{v}}_{\left(i\right)}^2}=1$. Among the 1,411 genes, 113 genes have non-zero leverage, and we call them top genes. Moreover, we notice that the first 25 genes have already achieved a cumulative leverage of 0.999, so we refer to them as primary genes. The remaining 88 top genes account for the remaining 0.001 leverage and are referred to as secondary genes (see Figure 2a for the visualization of this cut-off in a scree plot). We show in Figure 2b how these 113 top genes form a clear block structure in the differential matrix $\widehat{D}={\widehat{\sum }}_{\mathit{control}}-{\widehat{\sum }}_{\mathit{SCZ}}$. Notably, such a block structure cannot be revealed if ordered by the differentially expressed p-values (Figure 2c).

Fig. 2.

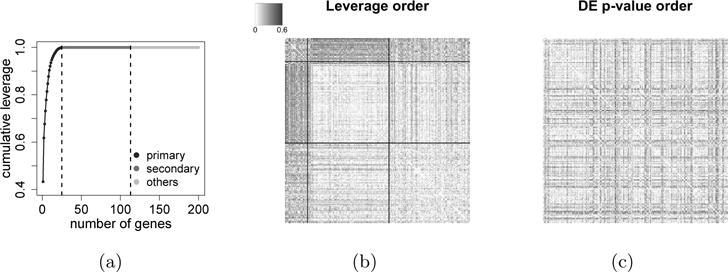
Visualization of 200 genes in the M2c module, including 25 primary genes that account for a total leverage of 0.999, 88 secondary genes that account for the remaining 0.001 leverage, and 87 randomly selected other genes that have zero leverage. (a) Scree plot of cumulative leverage. (b) Heatmap of $\left|\widehat{D}\right|$ where genes are ordered by leverage and a block structure is revealed. The two partitioning lines indicate the 25 primary genes and the 88 secondary genes. (c) Heatmap of $\left|\widehat{D}\right|$ where genes are ordered by p-values in differential expression analysis. Now the block structure is diluted.

Figure 2b reveals a significant decrease of gene co-expression (interactions) in cortical samples from SCZ subjects between the 25 primary genes and the 88 secondary genes. This pattern is more clearly illustrated in Figure 3, where two gene networks are constructed for these 113 top genes in control samples and SCZ samples separately (see Table 2 for gene names).

Fig. 3.

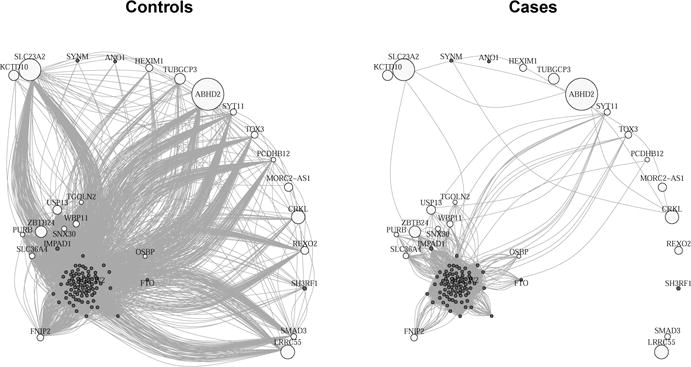
Gene networks constructed from control and SCZ samples, using top genes in the M2c module that have non-zero leverage. We exclude 6 genes that do not have annotated gene names, and show the remaining 22 primary genes (colored in white) and 85 secondary genes (colored in grey). The adjacency matrix is constructed by thresholding the absolute Pearson correlation |R_ij| at 0.5. Larger node sizes represent larger leverage.

Table 2.

Annotated names of 22 primary genes and 85 secondary genes in the M2c module, listed in the descending order of leverage. The 6 underlined genes are also significant in the differential expression analysis

	Gene names
Primary genes	ABHD2 SLC23A2 LRRC55 CRKL ZBTB24 TUBGCP3 KCTD10 USP13 MORC2-AS1 REXO2 HEXIM1 TOX3 FNIP2 WBP11 SYT11 SMAD3 SLC36A4 SNX30 PCDHB12 PURB TGOLN2 OSBP
Secondary genes	SH3RF1 IMPAD1 SYNM HECW2 ANO1 DNM3 STOX2 C1orf173 PPM1L DNAJC6 DLG2 LRRTM4 ANK3 EIF4G3 ANK2 ITSN1 SLIT2 LRRTM3 ATP8A2 CNTNAP2 CKAP5 GNPTAB USP32 USP9X ADAM23 SYNPO2 AKAP11 MAP1B KIAA1244 PPP1R12B SLC24A2 PTPRK SATB1 CAMTA1 MFSD6 KIAA1279 NTNG1 RYR2 RASAL2 PUM1 STAM ST8SIA3 ZKSCAN2 PBX1 ARHGAP24 RASA1 ANKRD17 MYCBP2 SLITRK1 BTRC MYH10 AKAP6 NRCAM MYO5A TRPC5 NRXN3 CACNA2D1 DNAJC16 GRIN2A KCNQ5 NETO1 FTO THRB NLGN1 HSPA12A BRAF OPRM1 KIAA1549L NOVA1 OPCML CEP170 DLGAP1 JPH1 LMO7 PCNX SYNJ1 RAPGEF2 NIPAL2 SYT1 UNC80 ATP8A1 SHROOM2 KCNJ6 SNAP91 WDR7

To shed light on the nature of the genes identified in the M2c module, we conduct a Gene Ontology (GO) enrichment analysis (Chen et al., 2013). The secondary gene list is most easily interpreted. It is highly enriched for genes directly involved in synaptic processes, both for GO Biological Process and Molecular Function. Two key molecular functions involve calcium channels/calcium ion transport and glutamate receptor activity. Under Biological Process, these themes are emphasized and synaptic organization emerges too. Synaptic function is a key feature that emerges from genetic findings for SCZ, including calcium channels/calcium ion transport and glutamate receptor activity (see Owen, Sawa and Mortensen (2016) for review).

For the primary genes, under GO Biological Process, “regulation of transforming growth factor beta2 (TGF-β2) production” is highly enriched. The top GO Molecular Function term is SMAD binding. The protein product of SMAD3 (one of the primary genes) modulates the impact of transcription factor TGF-β regarding its regulation of expression of a wide set of genes. TGF-β is important for many developmental processes, including the development and function of synapses (Diniz et al., 2012). Moreover, and notably, it has recently been shown that SMAD3 plays a crucial role in synaptogenesis and synaptic function via its modulation of how TGF-β regulates gene expression (Yu et al., 2014). It is possible that disturbed TGF-β signaling could explain co-expression patterns we observe in Figure 3, because this transcription factor will impact multiple genes. Another primary gene of interest is OSBP. Its protein product has recently been shown to regulate neural outgrowth and thus synaptic development (Gu et al., 2015). Thus perturbation of a set of genes could explain the pattern seen in Figure 3.

4.2. Robustness of the results

In this section, we illustrate that sLED remains powerful under perturbation of smoothing parameters and the boundaries of the M2c module. We first apply sLED with 1,000 permutations on the M2c module using c ∈ {0.10, 0.12, ⋯, 0 30}, (recall that $\sqrt{R}=c\sqrt{p}$). Each experiment is repeated 10 times, and the average p-value and the standard deviation for each experiment are shown in Figure 4a. All of the average p-values are smaller than 0.02. Note that larger values of c typically lead to denser solutions, which may hinder interpretability in practice. We also examine the stability of the list of 25 primary genes. For each value of c, we record the ranks of these 25 primary genes when ordered by leverage, and their average ranks with the standard deviations are visualized in Figure 4b. It is clear that these 25 primary genes are consistently the leading ones in all experiments.

Fig. 4.

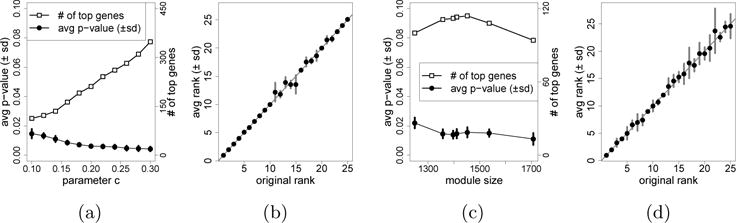
(a) sLED applied on the M2c module with c ∈ {0.10, ⋯, 0.30}. For each c we visualize the number of genes with non-zero leverage, as well as· the average and standard deviation of p-values in 10 repetitions, each using 1,000 permutations. (b) The average and standard deviation of ranks of the 25 primary genes when c ∈ {0.10, ⋯, 0.30}, where ranks are based on the descending order of leverage. (c) sLED applied on·7·modules using c = 0.1, including the original M2c module as well as 6 differently perturbed modules with sizes {1248, 1357, 1397, 1452, 1537, 1708}. For each (perturbed) module, we visualize the number of genes with non-zero leverage, as well as the average and standard deviation of p-values in 10 repetitions, each using 1,000 permutations. (d) The average and standard deviation of ranks of the 25 primary genes when sLED is applied on the 7 (perturbed) modules using c = 0.1, where ranks are based on the descending order of leverage.

Now we examine the robustness of sLED to perturbation of the module boundaries. Specifically, we perturb the M2c module by removing some genes that are less connected within the module, or including extra genes that are well-connected to the module. As suggested in Zhang and Horvath (2005), the selection of genes is based on their correlation with the eigengene (i.e., the first principal component) of the M2c module, calculated using the 279 control samples. By excluding the M2c genes with correlation smaller than {0.2, 0.3, 0.4}, we obtain three sub-modules with sizes {1397, 1357, 1248}, respectively. By including extra genes outside the M2c module with correlation larger than {0.75, 0.7, 0.65}, we obtain three sup-modules with sizes {1452, 1537, 1708}, respectively. We apply sLED with c = 0.1 and 1,000 permutations to these 6 perturbed modules. For each perturbed module, we examine the permutation p-values in 10 repetitions, as well as the ranks of the 25 primary genes when ordered by leverage. As shown in Figure 4c and Figure 4d, the results from sLED remain stable to such module perturbation.

4.3. Generalization to weighted adjacency matrices

Finally, we illustrate that sLED is not only applicable to testing differences in covariance matrices, but can also be applied to comparing general gene-gene “relationship” matrices. As an example, we consider the weighted adjacency matrix $A\in {\mathrm{ℝ}}^{p\times p}$, defined as

$$A_{ij}={\left|R_{ij}\right|}^{\beta },\text{for}1\le i,j\le p\text{and}\text{some}\text{constant}\beta >0,$$ (4.1)

where R_ij is the Pearson correlation between gene i and gene j, and the constant β > 0 controls the density of the corresponding weighted gene network. The weighted adjacency matrix is widely used as a similarity measurement for gene clustering, and has been shown to yield genetic modules that are biologically more meaningful than using regular correlation matrices (Zhang and Horvath, 2005). Now the testing problem becomes

$$H_0:\stackrel{\sim }{D}=0\text{versus}{H}_1:\stackrel{\sim }{D}\ne 0,$$

where $\stackrel{\sim }{D}=\mathbb{E}\left(A_{\mathit{control}}\right)-\mathbb{E}\left(A_{\mathit{SCZ}}\right)$. While classical two-sample covariance testing procedures are inapplicable under this setting, sLED can be easily generalized to incorporate this scenario. Let $\widehat{D}=A_{\mathit{control}}-A_{\mathit{SCZ}}$, then the same permutation procedure as described in Section 2.2 can be applied.

We explore the results of sLED for β ∈ {1, 3, 6.5, 9}, corresponding to four different choices of weighted adjacency matrices. We choose the same sparsity parameter c = 0.1 for sLED as in section 4.1, and with 1,000 permutations, the p-values are 0.020, 0.001, 0.002, and 0.006 for the 4 choices of β’s respectively. The latter three are significant at level 0.05 after a Bonferroni correction.

Interestingly, we find our results to be closely related to the connectivity of genes in the M2c module, where the connectivity of gene i is defined as

$$k_i={\displaystyle \sum _{j\ne i}{A}_{ij}}.$$

Figure 5 compares the gene connectivities between control and SCZ samples, where the top genes with non-zero leverage detected by sLED are highlighted. It is clear that the connectivity of genes is typically higher in control samples. Furthermore, as β increases, the differences on highly connected genes are enlarged, and consistently, the top genes detected by sLED also concentrate more and more on these “hub” genes that are densely connected. These genes would have been missed by the covariance matrix test, but are now revealed using weighted adjacency matrices. A Gene Ontology (GO) enrichment analysis (Chen et al., 2013) highlights a different, although related, set of biological processes when β = 9 versus β = 1 (Table 3).

Fig. 5.

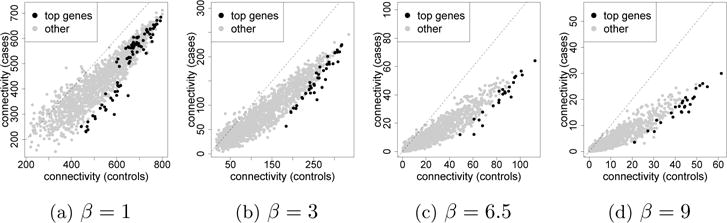
Connectivity in the M2c module for control and SCZ samples using weighted adjacency matrices with different β’s. The top genes detected by sLED with non-zero leverage are highlighted in black, and the auxiliary line y = x is shown in each plot.

Table 3.

Top 5 terms in Gene Ontology (GO) enrichment analysis on the top genes using weighted adjacency matrices with β ∈ {1, 9}. The adjusted p-values are reported in parentheses.

	β = 1	β = 9
1	Positive regulation of cell development (4.4e-05)	Synaptic transmission (5.6e-06)
2	Axon extension (4.6e-04)	Energy reserve metabolic process (6.5e-06)
3	Regulation of cell morphogenesis involved in differentiation (1.7e-04)	Divalent metal ion transport (4.1e-05)
4	Neuron projection extension (7.0e-04)	Divalent inorganic cation transport (4.5e-05)
5	Positive regulation of nervous system development (6.5e-04)	Calcium ion transport (2.8e-05)

5. Conclusion and discussion

In this paper, we propose sLED, a permutation test for two-sample covariance matrices under the high dimensional regime, which meets the need to understand the changes of gene interactions in complex human diseases. We prove that sLED achieves full power asymptotically; and in many biologically plausible settings, we verify by simulation studies that sLED outperforms many other existing methods. We apply sLED to a recently produced gene expression data set on Schizophrenia, and provide a list of 113 genes that show altered co-expression when brain samples from cases are compared to that from controls. We also reveal an interesting pattern of gene correlation change that has not been previously detected. The biological basis for this pattern is unclear. As more gene expression data become available, it will be interesting to validate these findings in an independent data set.

sLED can be applied to many other data sets for which signals are both sparse and weak. The performance is theoretically guaranteed for sub-Gaussian distributions, but we observe in simulation studies that sLED remains powerful when data has heavier tails. In terms of running time, on the 1,411 genes considered in this paper, sLED with 1,000 permutations takes 40 minutes using a single core on a computer equipped with an AMD Opteron(tm) Processor 6320 @ 2.8 GHz. When dealing with larger datasets, it is straightforward to parallelize the permutation procedure and further reduce the computation time.

Finally, we illustrate that sLED can be applied to a more general class of differential matrices between other gene-gene relationship matrices that are of practical interest. We show an example of comparing two weighted adjacency matrices and how this reveals novel insight on Schizophrenia. Although we have only stated the consistency results for testing covariance matrices, similar theoretical guarantee may be established for other relationship matrices as long as similar error bounds as in theorem 2 hold. This is a first step towards testing general high-dimensional matrices, and we leave a more thorough exploration in this direction to future work.