Enhancing Team Composition in Professional Networks: Problem Definitions and Fast Solutions

Abstract

In this paper, we study ways to enhance the composition of teams based on new requirements in a collaborative environment. We focus on recommending team members who can maintain the team’s performance by minimizing changes to the team’s skills and social structure. Our recommendations are based on computing team-level similarity, which includes skill similarity, structural similarity as well as the synergy between the two. Current heuristic approaches are one-dimensional and not comprehensive, as they consider the two aspects independently. To formalize team-level similarity, we adopt the notion of graph kernel of attributed graphs to encompass the two aspects and their interaction. To tackle the computational challenges, we propose a family of fast algorithms by (a) designing effective pruning strategies, and (b) exploring the smoothness between the existing and the new team structures. Extensive empirical evaluations on real world datasets validate the effectiveness and efficiency of our algorithms.

1 Introduction

In defining the essence of professional teamwork, Hackman and Katz [1] stated that teams function as ‘purposive social systems’, defined as people who are readily identifiable to each other by role and position and who work interdependently to accomplish one or more collective objectives. The responsibility for performing the various tasks and sub-tasks necessary to accomplish the team’s goal is divided and parceled-out among the team. Team effectiveness often depends upon the appropriate team structure and distribution of skills.

A promising algorithmic approach to team composition treats a team as a subgraph embedded in a larger social network. Prior research has focused on assembling a team from scratch while satisfying the skill requirements at minimum communication cost (e.g., diameter and minimum spanning tree) [2]. If the tasks arrive in an online fashion, the workload balance among the people needs to be considered [3]. In practical scenarios, there are more realistic requirements in the team formation, e.g., inclusion of a designated leader and size of a team [4]. With the increasing constraints, the team formation problem is NP-complete. Prior work to formulate automated ways of forming a team has used heuristic approaches (e.g., RarestFirst and SteinerTree) but so far lacks efficient solutions [2]. Our work differs from previous efforts in three ways: (1) we alter the composition of an existing team based on new requirements; (2) we solve the problem in a principled approach with the notation of graph kernel; and (3) we design a set of efficient algorithms.

Specifically, we address a family of problems under the scope of TEAM ENHANCEMENT, namely, (1) TEAM MEMBER REPLACEMENT, (2) TEAM REFINEMENT, (3) TEAM EXPANSION and (4) TEAM SHRINKAGE. TEAM MEMBER REPLACEMENT was first defined in [5], which concerns the churn of team members. For example, an employee in a software or sales team might decide to leave the organization and/or be assigned to a new task. The loss of a key member might lead to severe consequences for the team performance. The central question of TEAM MEMBER REPLACEMENT is how to find the best alternative from the rest network when a team member becomes unavailable. Different from TEAM MEMBER REPLACEMENT, TEAM REFINEMENT considers refining a team by replacing one member with another with the desired skill sets and communication connections. In the above two problems, the team size remains the same. In TEAM EXPANSION, we want to expand the team by adding a member with certain skill sets and communication structure. For instance, a software project team wants to develop a new feature of natural language search and a new member with Natural Language Processing (NLP) skill will be recruited. On the contrary, in TEAM SHRINKAGE, the size of a team needs to be reduced in response to new challenge such as a shortage of the available resource (e.g., a budget cut). In all cases, the resulting disruption [6] should be minimized.

By careful inspection, we identify the problem similarity between TEAM REFINEMENT, TEAM EXPANSION and TEAM MEMBER REPLACEMENT and propose these problems can be formulated in a way to share common technical solutions. In TEAM REFINEMENT, one team member is edited to a desired skill and network structure configuration. Since such edited member might not exist in the rest of the network, we call it a ‘virtual member’. By replacing this ‘virtual member’ as in TEAM MEMBER REPLACEMENT, we can solve TEAM REFINEMENT. Similarly, in TEAM EXPANSION, the desired new member might also be a ‘virtual member’. After adding this ‘virtual member’ to the current team and then replacing the ‘virtual member’, we can solve TEAM EXPANSION. We propose to reduce the disruption induced by the team alteration by maintaining the team-level similarity (between the original and the new teams), which includes skill similarity as well as structural similarity. The proposition is backed by some recent studies which show that team members prefer to work with people they have worked with before [7] and that distributed teams perform better when members know each other [8]. Furthermore, research has shown that specific communication patterns amongst team members are critical for performance [9].

We adopt the notion of graph similarity/kernel to characterize the team-level similarity for TEAM ENHANCEMENT. Through the lens of labeled graph for modeling teams, graph kernel can naturally capture the skill similarity and the structural similarity simultaneously. However, to solve TEAM MEMBER REPLACEMENT, TEAM REFINEMENT and TEAM EXPANSION on a team of size t in a network with n individuals and l skills, the basic approach would take O(nlr′t³) computations where r′ is the effective rank of the Kronecker product graph¹, which is computationally intractable. For example, for the DBLP² dataset with almost 1M users (i.e., n ≈ 1, 000, 000), we found that it would take 6,388s to find one replacement for a team of size 10. To address the computational challenges, we propose a family of fast algorithms by carefully designing the pruning strategies and metric analyses for exploring the smoothness and correspondences between the existing and the new teams. We perform the extensive empirical evaluations to demonstrate the effectiveness and efficiency of our methods. Specifically, we find that (1) by encoding both the skill and structural matching, we can achieve a much better replacement result. Compared with the best alternative choices, we achieve 27% and 24% net increase in average recall and precision, respectively (see Sec. 6.2 for details); (2) our fast algorithms are orders of magnitude faster and scale sublinearly. For example, our pruning strategy alone leads up to 1,709× speed-up, without sacrificing any accuracy.

The main contributions of this paper are as follows.

1. Problem Formulation. We formally define a family of problems under the scope of TEAM ENHANCEMENT, to alter the composition of a team in the context of networks where nodes carrying on multiple labels (skills) and edges representing social structures.

2. Algorithms and Analysis. We solve the problem by introducing graph kernels and propose a family of effective and scalable algorithms for TEAM ENHANCEMENT; and analyze the correctness and complexity.

3. Experimental Evaluations. We perform extensive experiments, including user studies and case studies, on real world datasets, to validate the effectiveness and efficiency of our methods.

The rest of the paper is organized as follows. Section 2 formally defines TEAM ENHANCEMENT problem. Section 3 presents our basic solutions. Section 4 addresses the computational challenges. Section 5 discusses the solutions for TEAM REFINEMENT, TEAM EXPANSION and TEAM SHRINKAGE. Section 6 presents the experimental results. Section 7 reviews some related work. Section 8 concludes the paper.

2 Problem Definitions

In this section, we formally define the family of TEAM ENHANCEMENT problems. Table 1 lists the main symbols used throughout this paper. We describe the n individuals by a labelled social network G := {A, L}, where A is an n × n adjacency matrix characterizing the connectivity among different individuals; and L is n × l skill indicator matrix. The i^th row vector of L describes the skill set of the i^th individual. For example, suppose there are only three skills in total, including {data mining, databases, information retrieval}. Then an individual with a skill vector [1, 1, 0] means that s/he has both data mining and databases skills but no skill in terms of information retrieval. L could be a binary matrix indicating the existence of a skill or a real matrix reflecting the strength of the skill. Also, we represent the elements in a matrix using a convention similar to Matlab, e.g., A(i, j) is the element at the i^th row and j^th column of the matrix A, and A(:, j) is the j^th column of A, etc. For the i^th individual, we define the associated skill vector as l = L(i, :) and communication structure vector as a = A(i, :).

TABLE 1.

Table of symbols

Symbols	Definition
G := {A, L}	the entire social network
An×n	the adjacency matrix of G
Ln×l	skill indicator matrix
$\mathcal{T}$	the team member index
$\mathbf{G}(\mathcal{T})$	the team network indexed by its members $\mathcal{T}$
di	the degree of the ith node in A
l	the total number of skills
t	the team size, i.e., $t=\left|\mathcal{T}\right|$
n	the total number of individuals in A
m	the total number of connections in A

We use the calligraphic letter $\mathcal{T}$ to index the members of a team, which includes a subset of t = $t=\left|\mathcal{T}\right|$ out of n individuals. Correspondingly, we can represent the team by another labelled team network $\mathbf{G}(\mathcal{T}):=\{\mathbf{A}(\mathcal{T},\mathcal{T})\mathbf{L}(\mathcal{T},:)\}$. Note that $\mathbf{A}(\mathcal{T},\mathcal{T})$ and $\mathbf{L}(\mathcal{T},:)$ are sub-matrices of A and L, respectively. If we replace an existing member $p\in \mathcal{T}$ of a given team $\mathcal{T}$ by another individual $q\notin \mathcal{T}$, the new team members are indexed by ${\mathcal{T}}_{p\to q}:=\{\mathcal{T}/p,q\}$; and the new team is represented by the labelled network $\mathbf{G}({\mathcal{T}}_{p\to q})$. If we lay off an existing member $p\in \mathcal{T}$ of a given team $\mathcal{T}$, the new team members are indexed by ${\mathcal{T}}_{/p}:=\{\mathcal{T}/p\}$; and the new team is represented by the labelled network $\mathbf{G}({\mathcal{T}}_{/p})$.

With the above notations and assumptions, our problems can be formally defined as follows:

• Problem 1. TEAM MEMBER REPLACEMENT

  Given: (1) A labelled social network G := {A, L}, (2) a team $\mathbf{G}(\mathcal{T})$, and (3) a team member $p\in \mathcal{T}$;

  Recommend: An alternate $q\notin \mathcal{T}$ to replace the person p’s role in the team $\mathbf{G}(\mathcal{T})$.

• Problem 2. TEAM REFINEMENT

  Given: (1) A labelled social network G := {A, L}, (2) a team $\mathbf{G}(\mathcal{T})$, (3) a team member $p\in \mathcal{T}$, and (4) desired skill l and communication structure a for p;

  Recommend: A candidate $q\notin \mathcal{T}$ with skill l and communication structure a to refine the person p’s role in the team $\mathbf{G}(\mathcal{T})$.

• Problem 3. TEAM EXPANSION

  Given: (1) A labelled social network G := {A, L}, (2) a team $\mathbf{G}(\mathcal{T})$, and (3) desired skill l and communication structure a for a new member;

  Recommend: A new member $q\notin \mathcal{T}$ with skill l and communication structure a to join the team $\mathbf{G}(\mathcal{T})$.

• Problem 4. TEAM SHRINKAGE

  Given: (1) A labelled social network G := {A, L}, and (2) a team $\mathbf{G}(\mathcal{T})$;

  Recommend: A member $p\in \mathcal{T}$ to leave the team $\mathbf{G}(\mathcal{T})$.

Next, we will introduce our designed “goodness” metric for ranking the candidates.

3 Team Member Replacement: Proposed Solutions

In this section, we present our solutions for TEAM MEMBER REPLACEMENT. We start with the design objectives for the TEAM MEMBER REPLACEMENT problem, present graph kernel as the basic solution to fulfill such design objectives; and finally analyze the main computational challenges. We postpone the discussion on TEAM REFINEMENT, TEAM EXPANSION and TEAM SHRINKAGE in Section 5.

3.1 Design Objectives

Generally speaking, we want to find a similar person q to replace the current team member p who is about to leave the team. Natually, the replacement q should have a similar skill set as the current member q in order to perform the (sub)tasks q is involved in. More importantly, as recent studies show, team members prefer to work with people they have developed strong working relationships in the past [7]. This suggests a good replacement should also bring a similar social relationships with the team members. That is, a good replacement q should not only have a similar skill set as team member p; but also maintains team cohesion defined by similar social connectivity and fostering good chemistry among the team members and/or being less disrupted. Defining the team context is critical. In other words, the similarity between individuals should be measured in the context of the team itself. Often, the success of a team largely depends on the successful execution of several sub-tasks, each of which requires the cooperation among several team members with certain skill configurations. For example, several classic tactics often recurringly find themselves in a successful NBA team, including (a) triangle offense (which is featured by a sideline triangle created by the center, the forward, and the guard), (b) pick and roll (which involves the cooperation between two players - one plays as ‘pivot’ and the other plays as ‘screen’, respectively), etc. Generally speaking, team performance arises from the shared knowledge and experience amongst team members and their ability to share and coordinate their work. As noted in the introduction, a specific pattern of communication is associated with higher team performance. Maintaining that communication structure should therefore be less disruptive to the team.

If we translate these requirements into the notations defined in Section 2, it naturally leads to the following two design objectives for a good TEAM MEMBER REPLACEMENT:

• Skill matching: the new member should bring a similar skill set as the current team member p to be replaced that are required by the team.

• Structural matching: the new member should have similar connects to the rest of the team members as team member p.

3.2 Basic Solutions

In order to fulfill the above two design objectives, we need a similarity measure between two individuals in the context of the team itself that captures both skill matching and the structural matching as well as the interaction of both. We refer to this kind of similarity as team context aware similarity. Mathematically, the so-called graph kernel defined on the current and new teams provides a natural tool for such a team context aware similarity. That is, we want to find a replacement person q as

$$q={\text{argmax}}_{j,j\notin \mathcal{T}}\text{Ker}(\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{p\to j}))$$ (1)

In Eq. (1), $\mathbf{G}(\mathcal{T})$ is the labelled team graph; and $\mathbf{G}({\mathcal{T}}_{p\to j})$ is the labelled team graph after we replace a team member p by another individual j; and Ker(.) is the kernel between these two labelled graphs. Generally speaking, the basic idea of various graph kernels is to compare the similarity of the sub-graphs between the two input graphs and then aggregate them as the overall similarity between the two graphs. As such, the graph kernel is able to simultaneously capture both the skill matching and the structure matching, beyond the simple ad-hoc combination between the two (e.g., weighted linear combination, multiplicative combination, sequential filtering, etc). We would like to emphasize that this treatment is important - as we will show in the experimental section, it leads to much better performance over all the alternative choices. Let us explain the intuition/rationality of why graph kernel is a natural choice for team context aware similarity. Here, each subgraph in a given team might reflect a specific skill configuration among a sub-group of team members that is required by a certain sub-task of that team. By comparing the similarity between two subgraphs, we implicitly measure the capability of the individual j to perform this specific sub-task. Thus, by aggregating the similarities of all the possible subgraphs between the two input graphs/teams, we get a goodness measure of the overall capability of the individual j to perform all the potential sub-tasks that team member p is involved in the original team. Note that the team replacement scenario is different from team formation [2, 3, 4]. This existing work on team formation aims to build a team from scratch by optimizing some pre-chosen metric (e.g., compatibility, diversity, etc). In contrast, we aim to find a new team member such that the new team resembles the original team as much as possible. Team formation is typically an effortful and prolonged process (weeks, months, years) and team training is hugely resource intensive. For instance, teams usually go through several stages - the most popular model being “storming, forming, norming, performing”. Our approach is focused on maintaining team cohesion and ideally high-levels of performance by recommending the most ideal candidate to minimize any disruption.

Having this in mind, many of the existing graph kernels can be adopted in Eq. (1), such as random walk based graph kernels, sub-tree based graph kernels (See section 7 for a review). In this paper, we focus on the random walk based graph kernel [11] due to its mathematical elegancy and superior empirical performance. Given two labelled graphs G_i := {A_i, L_i}, i = 1, 2, the random walk based graph kernel between them can be formally computed as follows [11, 12]:

$$\text{Ker}({\mathbf{G}}_1,{\mathbf{G}}_2)=\mathbf{y}\prime {(\mathbf{I}-c{\mathbf{A}}_{\times })}^{-1}{\mathbf{L}}_{\times }\mathbf{x}$$ (2)

where ${\mathbf{A}}_{\times }={\mathbf{L}}_{\times }({\mathbf{A}}_1^{\prime }\otimes {\mathbf{A}}_2^{\prime })$ is the weight matrix of the two graphs’ Kronecker product, ⊗ represents the Kronecker product between two matrices, c is a decay factor, y = y₁ ⊗ y₂ and x = x₁ ⊗ x₂ are the so-called starting and stopping vectors to indicate the weights of different nodes and are set uniform in our case, L_× is a diagonal matrix where L_×(i, i) = 0 if the i^th row of $({\mathbf{A}}_1^{\prime }\otimes {\mathbf{A}}_2^{\prime })$ is zeroed out due to label inconsistency of two nodes of the two graphs. L_× can be expressed as ${\mathbf{L}}_{\times }={\displaystyle {\sum }_{k=1}^l\text{diag}({\mathbf{L}}_1(:,k))\otimes \text{diag}({\mathbf{L}}_2(:,k))}$.

3.3 Computational Challenges

Eq.(2) naturally suggests the following procedure for solving TEAM MEMBER REPLACEMENT problem (referred to as TEAMREP-BASIC): for each individual $j\notin \mathcal{T}$, we compute its score score(j) by Eq.(2); and recommend the individual(s) with the highest score(s). However, this strategy (TEAMREP-BASIC) is computationally intensive since we need to compute many random walk based graph kernels and each of such computations could be expensive especially when the team size is large. To be specific, for a team $\mathcal{T}$ of size t and a graph G with n individuals and l skills in total, its time complexity is O(nlr′t³) where r′ is the effective rank of A_× since we need to compute a random walk based graph kernel for each candidate who is not in the current team, each of which could cost O(lr′t³) [11]. Even if we allow some approximation in computing each of these graph kernels, the best known algorithms (i.e., by [12]) would still give an overall time complexity as O(n(lt²r⁴ + mr + r⁶)), where r is reduced rank after low rank approximation, which is still too high. For example, on the DBLP dataset with 916,978 authors, for a team with 10 members, it would take 6,388s to find a best replacement.

In the next section, we present our solution to remedy these computational challenges.

4 Team Member Replacement: Scale-Up and Speed-Up

In this section, we address the computational challenges to scale up and speed up TEAMREP-BASIC. We start with an efficient pruning strategy to reduce the number of graph kernel computations, and then present three algorithms to speed-up the computation of individual graph kernel.

4.1 Scale-up: Candidate Filtering

Here, we propose an efficient pruning strategy to filter out those unpromising candidates. Recall that one of our design objectives for a good TEAM MEMBER REPLACEMENT is structural matching, i.e., the new member has a similar network structure as team member p in connecting the rest team members. Since p is connected to at least some of the rest members, it suggests that if an individual does not have any connection to any of the rest team members, s/he might not be a good candidate for replacement.

Pruning Strategy

Filter out all the candidates who do not have any connections to any of the rest team members.

Lemma 1

Effectiveness of Pruning. For any two persons i and j not in $\mathcal{T}$, if i is connected to at least one member in $\mathcal{T}/p$ and j has no connections to any of the members in $\mathcal{T}/p$, we have that

$$\mathit{\text{Ker}}(\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{p\to i}))\ge \mathit{\text{Ker}}(\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{p\to j})).$$

Proof

Suppose that $\mathbf{G}(\mathcal{T}):=\{{\mathbf{A}}_0,{\mathbf{L}}_0\}$. Let $\mathbf{G}({\mathcal{T}}_{p\to i}):=\{{\mathbf{A}}_1,{\mathbf{L}}_1\}$, and $\mathbf{G}({\mathcal{T}}_{p\to j}):=\{{\mathbf{A}}_2,{\mathbf{L}}_2\}$.

By Taylor expansion of Eq. (2), we have

$$\text{Ker}(\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{p\to i}))={\displaystyle {\sum }_{z=0}^{\infty }c\mathbf{y}\prime }{({\mathbf{L}}_{\times 1}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_1^{\prime }))}^z\mathbf{x},$$

where ${\mathbf{L}}_{\times 1}={\displaystyle {\sum }_{k=1}^l\text{diag}({\mathbf{L}}_0(:,k))\otimes \text{diag}({\mathbf{L}}_1(:,k))}$,

$$\text{Ker}(\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{p\to j}))={\displaystyle {\sum }_{z=0}^{\infty }c\mathbf{y}\prime }{({\mathbf{L}}_{\times 2}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_2^{\prime }))}^z\mathbf{x},$$

where ${\mathbf{L}}_{\times 2}={\displaystyle {\sum }_{k=1}^l\text{diag}({\mathbf{L}}_0(:,k))\otimes \text{diag}({\mathbf{L}}_2(:,k))}$.

Therefore, it is sufficient to show that ${({\mathbf{L}}_{\times 1}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_1^{\prime }))}^z\ge {({\mathbf{L}}_{\times 2}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_2^{\prime }))}^z$ for any z > 0, where two matrices A ≥ B if A_ij ≥ B_ij holds for all possible (i, j). We prove this by induction.

(Base Case of Induction) When z = 1, we have

$$\begin{array}{l}{\mathbf{L}}_{\times 1}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_1^{\prime })\\ =\left({\displaystyle {\sum }_{k=1}^l\text{diag}({\mathbf{L}}_0(:,k))\otimes \text{diag}({\mathbf{L}}_1(:,k))}\right)({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_1^{\prime })\\ ={\displaystyle {\sum }_{k=1}^l\text{(diag}({\mathbf{L}}_0(:,k)){\mathbf{A}}_0^{\prime })\otimes (\text{diag}({\mathbf{L}}_1(:,k)){\mathbf{A}}_1^{\prime }).}\end{array}$$ (3)

Because $\text{(diag}({\mathbf{L}}_1(:,k)){\mathbf{A}}_1^{\prime })\ge (\text{diag}({\mathbf{L}}_2(:,k)){\mathbf{A}}_2^{\prime })$, we have ${\mathbf{L}}_{\times 1}{({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_1^{\prime }))}^z\ge ({\mathbf{L}}_{\times 2}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_2^{\prime })$.

(Induction Step) Assuming ${({\mathbf{L}}_{\times 1}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_1^{\prime }))}^{z-1}\ge {({\mathbf{L}}_{\times 2}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_2^{\prime }))}^{z-1}$, we have that

$$\begin{array}{c}{({\mathbf{L}}_{\times 1}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_1^{\prime }))}^z\ge {({\mathbf{L}}_{\times 2}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_2^{\prime }))}^{z-1}({\mathbf{L}}_{\times 1}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_1^{\prime }))\\ \ge {({\mathbf{L}}_{\times 2}({\mathbf{A}}_0^{\prime }\otimes {\mathbf{A}}_2^{\prime }))}^z\end{array}$$

where the first inequality is due to the induction assumption; and the second inequality is due to the base case. This completes the proof.

Remarks

By Lemma 1, our pruning strategy is “safe”, i.e., it will not miss any potentially good replacements. In the meanwhile, we can reduce the number of graph kernel computations from O(n) to $O\left({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i}\right)$, which is sub-linear in n.

4.2 Speedup Graph Kernel - Exact Approach

Here, we address the problem of speeding up the computation of an individual graph kernel. Let $\mathbf{G}(\mathcal{T}):=\{{\mathbf{A}}_1,{\mathbf{L}}_1\}$ and $\mathbf{G}({\mathcal{T}}_{p\to q}):=\{{\mathbf{A}}_2,{\mathbf{L}}_2\}$, where A₁, A₂ are symmetric adjacency matrices of the two graphs.³ Without loss of generality, let us assume that p is the last team member in $\mathcal{T}$. Compare A₁ with A₂, it can be seen that the only difference is their last columns and last rows. Therefore, we can rewrite A₂ as A₂ = A_c + A_d2, where A_c is A₁ with its last row and column being zeroed out, and the nonzero elements of A_d2 only appear in its last row and column reflecting the connectivity of q to the new team. Notice that A_d2 has a rank at most 2, so it can be factorized into two smaller matrices as A_d2 = E_t×2F_2×t.

Denote diag(L₁(:, j)) as ${\mathbf{L}}_1^{(j)}$ and diag(L₂(:, j)) as ${\mathbf{L}}_2^{(j)}$ for j = 1,…, l. Compare ${\mathbf{L}}_1^{(j)}$ with ${\mathbf{L}}_2^{(j)}$, the only difference is the last diagonal element. Therefore, we can write ${\mathbf{L}}_2^{(j)}$ as ${\mathbf{L}}_2^{(j)}={\mathbf{L}}_c^{(j)}+{\mathbf{L}}_{d2}^{(j)}$, where ${\mathbf{L}}_c^{(j)}$ is ${\mathbf{L}}_1^{(j)}$ with last element zeroed out, and ${\mathbf{L}}_{d2}^{(j)}$’s last element indicates q’s strength of having the j^th skill. ${\mathbf{L}}_2^{(j)}$’s rank is at most 1, so it can be factorized as ${\mathbf{L}}_2^{(j)}={\mathbf{e}}_{t\times 1}^{(j)}+{\mathbf{f}}_{1\times t}^{(j)}$. Therefore, the exact graph kernel for the labelled graph can be computed as:

$$\begin{array}{l}\text{Ker}(\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{p\to q}))\\ =\mathbf{y}\prime (\mathbf{I}-c({\displaystyle {\sum }_{j=1}^l{\mathbf{L}}_1^{(j)}\otimes {\mathbf{L}}_2^{(j)}})({\mathbf{A}}_1^{\prime }\otimes {\mathbf{A}}_2^{\prime })){ }^{-1}({\displaystyle {\sum }_{j=1}^l{\mathbf{L}}_1^{(j)}\otimes {\mathbf{L}}_2^{(j)}})\mathbf{x}\\ =\mathbf{y}\prime \underset{\mathbf{Z}:\text{invariant}\mathrm{w}\text{.r.t}.q}{\underbrace{(\mathbf{I}-c({\displaystyle \sum _{j=1}^l{\mathbf{L}}_1^{(j)}\otimes {\mathbf{L}}_c^{(j)}})({\mathbf{A}}_1\otimes {\mathbf{A}}_c)}}\\ -c\underset{\mathbf{P}\mathbf{Q}({\mathbf{A}}_1\otimes {\mathbf{A}}_c)=\mathbf{P}{\mathbf{Y}}_1}{\underbrace{({\displaystyle \sum _{j=1}^l({\mathbf{L}}_1^{(j)}\otimes {\mathbf{e}}^{(j)}})(\mathbf{I}\otimes {\mathbf{f}}^{(j)}))({\mathbf{A}}_1\otimes {\mathbf{A}}_c)}}\\ -c\underset{{\mathbf{X}}_1{\mathbf{Y}}_2}{\underbrace{({\displaystyle \sum _{j=1}^l({\mathbf{L}}_1^{(j)}\otimes {\mathbf{L}}_c^{(j)}})({\mathbf{A}}_1\otimes \mathbf{E})(\mathbf{I}\otimes \mathbf{F})}}\\ -c\underset{{\mathbf{X}}_2{\mathbf{Y}}_2}{\underbrace{{({\displaystyle \sum _{j=1}^l({\mathbf{L}}_1^{(j)}\otimes {\mathbf{e}}^{(j)}})(\mathbf{I}\otimes {\mathbf{f}}^{(j)}))({\mathbf{A}}_1\otimes \mathbf{E})(\mathbf{I}\otimes \mathbf{F}))}^{-1}}}\\ ({\displaystyle {\sum }_{j=1}^l{\mathbf{L}}_1^{(j)}\otimes {\mathbf{L}}_2^{(j)}})\mathbf{x}.\end{array}$$ (4)

Each ${\mathbf{L}}_1^{(j)}\otimes {\mathbf{e}}^{(j)}$ is a matrix of size t² by t and I ⊗ f^(j) is a matrix of size t by t². We denote the matrix created by concatenating all ${\mathbf{L}}_1^{(j)}\otimes {\mathbf{e}}^{(j)}$ horizontally as P, i.e., $\mathbf{P}=[{\mathbf{L}}_1^{(1)}\otimes {\mathbf{e}}^{(1)},\dots ,{\mathbf{L}}_1^{(l)}\otimes {\mathbf{e}}^{(l)}]$; denote the matrix created by stacking all I ⊗ f^(j) vertically as Q, i.e., Q = [I ⊗ f⁽¹⁾;…; I ⊗ f^(l)]. Obviously, $({\displaystyle {\sum }_{j=1}^l({\mathbf{L}}_1^{(j)}\otimes {\mathbf{e}}^{(j)}})(\mathbf{I}\otimes {\mathbf{f}}^{(j)}))$ is equal to PQ. We denote $({\displaystyle {\sum }_{j=1}^l{\mathbf{L}}_1^{(j)}\otimes {\mathbf{L}}_c^{(j)}})({\mathbf{A}}_1\otimes \mathbf{E})$ by X₁; denote $({\displaystyle {\sum }_{j=1}^l({\mathbf{L}}_1^{(j)}\otimes {\mathbf{e}}^{(j)}})(\mathbf{I}\otimes {\mathbf{f}}^{(j)}))({\mathbf{A}}_1\otimes \mathbf{E})$ by X₂; denote Q(A₁ ⊗ A_c) by Y₁ and denote (I ⊗ F) by Y₂. Let X be [P, X₁, X₂] and Y be [Y₁; Y₂; Y₂].

With these additional notations, we can rewrite Eq. (4) as

$$\begin{array}{l}\text{Ker}(\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{p\to q}))={\mathbf{y}}^{\prime }{(\mathbf{Z}-c\mathbf{X}Y)}^{-1}({\displaystyle {\sum }_{j=1}^l{\mathbf{L}}_1^{(j)}\otimes {\mathbf{L}}_2^{(j)}})\mathbf{x}\\ ={\mathbf{y}}^{\prime }({\mathbf{Z}}^{-1}+c{\mathbf{Z}}^{-1}\mathbf{X}{(\mathbf{I}-c\mathbf{Y}{\mathbf{Z}}^{-1}\mathbf{X})}^{-1}\mathbf{Y}{\mathbf{Z}}^{-1})\\ (({\displaystyle {\sum }_{j=1}^l{\mathbf{L}}_1^{(j)}\otimes {\mathbf{L}}_c^{(j)}})\mathbf{x}+({\displaystyle {\sum }_{j=1}^l({\mathbf{L}}_1^{(j)}\otimes {\mathbf{e}}^{(j)})}(\mathbf{I}\otimes {\mathbf{f}}^{(j)}))\mathbf{x}),\end{array}$$ (5)

where the second equation is due to the matrix inverse lemma [13].

Remarks

In Eq. (5), $\mathbf{Z}=\mathbf{I}-c({\displaystyle {\sum }_{j=1}^l{\mathbf{L}}_1^{(j)}\otimes {\mathbf{L}}_c^{(j)}})({\mathbf{A}}_1\otimes {\mathbf{A}}_c)$ does not depend on the candidate q. Thus, if we pre-compute its inverse Z⁻¹, we only need to update X(I − cYZ⁻¹X)⁻¹Y and PQx for every new candidate. Notice that compared with the original graph kernel (the first equation in Eq. (4)), (I−cYZ⁻¹X) is a much smaller matrix of (l + 4)t × (l + 4)t. In this way, we can accelerate the process of computing its inverse without losing the accuracy of graph kernel.

4.3 Speedup Graph Kernel - Approx Approach

Note that the graph kernel by Eq. (5) is exactly the same as the original method by the first equation in Eq. (4). If we allow some approximation error, we can further speed-up the computation.

Note that A_c is symmetric and its rank-r approximation can be written as Â_c = UV, where U is a matrix of size t by r and V is a matrix of size r by t. A₁ can be approximated as Â₁ = Â_c + A_d1 = UV + E₁F₁ = X₁Y₁, where X₁ = [U, E₁], Y₁ = [V; F₁], E₁ = [w₁, s], ${\mathbf{F}}_1=[\mathbf{s}\prime ;{\mathbf{w}}_1^{\prime }]$, s is a zero vector of length t except that the last element is 1, and w₁ is the weight vector from p to the members in $\mathcal{T}$. Similarly, after p is replaced by a candidate q, the weight matrix of the new team can be approximated as Â₂ = X₂Y₂ where X₂ = [U, E₂], Y₂ = [V; F₂], E₂ = [w₂, s], ${\mathbf{F}}_2=[\mathbf{s}\prime ;{\mathbf{w}}_2^{\prime }]$ and w₂ is the weight vector from q to the members in the new team. The approximated graph kernel for labeled graphs can be computed as:

$$\begin{array}{l}\widehat{\mathrm{K}}\text{er}(\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{p\to q}))={\mathbf{y}}^T{(\mathbf{I}-c{\mathbf{L}}_{\times }({\widehat{\mathbf{A}}}_1^{\prime }\otimes {\widehat{\mathbf{A}}}_2^{\prime }))}^{-1}{\mathbf{L}}_{\times }\mathbf{x}\\ ={\mathbf{y}}^{\prime }{(\mathbf{I}-c{\mathbf{L}}_{\times }({\mathbf{X}}_1{\mathbf{Y}}_1)\otimes ({\mathbf{X}}_2{\mathbf{Y}}_2))}^{-1}{\mathbf{L}}_{\times }\mathbf{x}\\ ={\mathbf{y}}^{\prime }{(\mathbf{I}-c{\mathbf{L}}_{\times }({\mathbf{X}}_1\otimes {\mathbf{X}}_2)({\mathbf{Y}}_1\otimes {\mathbf{Y}}_2))}^{-1}{\mathbf{L}}_{\times }\mathbf{x}\\ ={\mathbf{y}}^{\prime }(\mathbf{I}+c{\mathbf{L}}_{\times }({\mathbf{X}}_1\otimes {\mathbf{X}}_2)\mathbf{M}({\mathbf{Y}}_1\otimes {\mathbf{Y}}_2)){\mathbf{L}}_{\times }\mathbf{x}\\ ={\mathbf{y}}^{\prime }{\mathbf{L}}_{\times }\mathbf{x}+c{\mathbf{y}}^{\prime }\left({\displaystyle {\sum }_{j=1}^l{\mathbf{L}}_1^{(j)}{\mathbf{X}}_1\otimes {\mathbf{L}}_2^{(j)}{\mathbf{X}}_2}\right)\mathbf{M}({\mathbf{Y}}_1\otimes {\mathbf{Y}}_2)){\mathbf{L}}_{\times }\mathbf{x}\\ =\left({\displaystyle {\sum }_{j=1}^l({\mathbf{y}}_1^{\prime }{\mathbf{L}}_1^{(j)}{\mathbf{x}}_1)({\mathbf{y}}_2^{\prime }{\mathbf{L}}_2^{(j)}{\mathbf{x}}_2)}\right)+c\\ \left({\displaystyle {\sum }_{j=1}^l{\mathbf{y}}_1^{\prime }{\mathbf{L}}_1^{(j)}{\mathbf{X}}_1\otimes }{\mathbf{y}}_2^{\prime }{\mathbf{L}}_2^{(j)}{\mathbf{x}}_2\right)\mathbf{M}\left({\displaystyle {\sum }_{j=1}^l{\mathbf{Y}}_1{\mathbf{L}}_1^{(j)}{\mathbf{x}}_1\otimes {\mathbf{Y}}_2{\mathbf{L}}_2^{(j)}{\mathbf{x}}_2}\right),\end{array}$$ (6)

where $\mathbf{M}={\left(\mathbf{I}-c\left({\displaystyle {\sum }_{j=1}^l{\mathbf{Y}}_1{\mathbf{L}}_1^{(j)}{\mathbf{X}}_1\otimes {\mathbf{Y}}_2{\mathbf{L}}_2^{(j)}{\mathbf{X}}_2}\right)\right)}^{-1}$, the second equation is due to the Kronecker product property; the third equation is again due to the matrix inverse lemma, the fourth equation is by matrix multiplication distributivity and the last equation is due to the Kronecker product property.

Remarks

The computation of M is much cheaper than the original graph kernel since it is a matrix inverse of size (r+2)² ×(r+2)². It was first proposed in [12] to explore the low-rank structure of the input graphs to speed-up graph kernel computations. However, in the context of TEAM MEMBER REPLACEMENT, we would need to estimate the low-rank approximation many times $\left(O\left({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i}\right)\right)$ when we directly apply the method in [12]. In contrast, we only need to compute top-r approximation once by Eq. (6). As our complexity analysis (subsection 4.5) and experimental evaluations (subsection 6.3) show, this brings a few times additional speed-up.

4.4 Speedup Graph Kernel - Approximation with Correspondence

In the above approaches, the starting and ending probabilities x and y are assumed to be uniform by default. This implicitly implies that the starting points for random walks on the two team graphs could be any combinations. However, the node correspondences between the two teams are already known. For example, suppose the members in the old team are $\mathcal{T}=\{a,b,c\}$ and the new team after replacement becomes ${\mathcal{T}}_{c\to d}=\{a,b,d\}$. Then a, b, c in the original team correspond to a, b, d respectively in the new team. With the correspondence known, we can only consider those random walks starting from the correspondent nodes only. In the above example, only random walks starting from (a, a), (b, b), (c, d) should be considered. If we assign equal starting probabilities for the correspondent starting nodes and zero for else, the starting probability x can be written as:

$$\mathrm{x}=\frac{1}{t}[\underset{t}{\underbrace{1,0,0,\dots ,0,}}\underset{t}{\underbrace{0,1,0,\dots ,0,}}\dots ,\underset{t}{\underbrace{0,0,0,\dots ,1}}]\prime$$ (7)

Similarly, by the same reasoning, we get y = x. The computations in Eq. (6) can be further simplified as follows:

$$\begin{array}{c}\mathbf{y}\prime {\mathbf{L}}_{\times }\mathbf{x}=\frac{1}{t^2}{\displaystyle {\sum }_{i=1}^t{\displaystyle {\sum }_{j=1}^l{\mathbf{L}}_1^{(j)}(i,i)\cdot {\mathbf{L}}_2^{(j)}(i,i)}}\\ ({\mathbf{Y}}_1\otimes {\mathbf{Y}}_2){\mathbf{L}}_{\times }\mathbf{x}=\frac{1}{t}{\displaystyle \sum _{i=1}^t({\displaystyle \sum _{j=1}^l{\mathbf{L}}_1^{(j)}(i,i)\cdot {\mathbf{L}}_2^{(j)}(i,i)})}\\ {\mathbf{Y}}_1(:,i)\otimes {\mathbf{Y}}_1(:,i)\\ \mathbf{y}\prime {\mathbf{L}}_{\times }({\mathbf{X}}_1\otimes {\mathbf{X}}_2)=\frac{1}{t}{\displaystyle \sum _{i=1}^t({\displaystyle \sum _{j=1}^l{\mathbf{L}}_1^{(j)}(i,i)\cdot {\mathbf{L}}_2^{(j)}(i,i)})}\\ {\mathbf{X}}_1(i,:)\otimes {\mathbf{X}}_1(i,:).\end{array}$$ (8)

The approximated graph kernel for labeled graphs with node correspondence can be computed as:

$$\begin{array}{l}\widehat{K}\text{er}(\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{p\to q}))={\mathbf{y}}^T{(\mathbf{I}-c{\mathbf{L}}_{\times }({\widehat{\mathbf{A}}}_1^{\prime }\otimes {\widehat{\mathbf{A}}}_2^{\prime }))}^{-1}{\mathbf{L}}_{\times }\mathbf{x}\\ ={\mathbf{y}}^{\prime }{\mathbf{L}}_{\times }\mathbf{x}+c{\mathbf{y}}^{\prime }{\mathbf{L}}_{\times }({\mathbf{X}}_1\otimes {\mathbf{X}}_2)\mathbf{M}({\mathbf{Y}}_1\otimes {\mathbf{Y}}_2){\mathbf{L}}_{\times }\mathbf{x}\\ =\frac{1}{t^2}{\displaystyle \sum _{i=1}^t{\displaystyle \sum _{j=1}^l{\mathbf{L}}_1^{(j)}(i,i)\cdot {\mathbf{L}}_2^{(j)}(i,i)}}+\frac{c}{t^2}({\displaystyle \sum _{i=1}^t({\displaystyle \sum _{j=1}^l{\mathbf{L}}_1^{(j)}(i,i)\cdot {\mathbf{L}}_2^{(j)}(i,i)})}\\ {\mathbf{X}}_1(i,:)\otimes {\mathbf{X}}_2(i,:))\mathbf{M}({\displaystyle \sum _{i=1}^t({\displaystyle \sum _{j=1}^l{\mathbf{L}}_1^{(j)}(i,i)\cdot {\mathbf{L}}_2^{(j)}(i,i)})}\\ {\mathbf{Y}}_1(:,i)\otimes {\mathbf{Y}}_2(:,i))\end{array}$$ (9)

Remarks

As shown in Eq. (8), the savings from the correspondences come from the way y′L_×x, (Y₁ ⊗ Y₂)L_×x and y′L_×(X₁ ⊗ X₂) are computed. For example, without correspondence, computing (Y₁ ⊗ Y₂)L_×x by ${\displaystyle {\sum }_{j=1}^l{\mathbf{Y}}_1}{\mathbf{L}}_1^{(j)}{\mathbf{x}}_1\otimes {\mathbf{Y}}_2{\mathbf{L}}_2^{(j)}{\mathbf{x}}_2$ will take O(lt²r + lr²) in Eq. (6), but it only takes O(tl + tr²) in Eq. (9).

4.5 Putting Everything Together

Putting everything together, we are ready to present our algorithms for TEAM MEMBER REPLACEMENT. Depending on the specific methods for computing the individual graph kernels, we propose three variants.

4.5.1 Variant #1: TEAMREP-FAST-EXACT

We first present our algorithm using the exact graph kernel computation in Eq. (5). The algorithm (TEAMREP-FAST-EXACT) is summarized in Algorithm 1. We only need to pre-compute and store Z⁻¹, R, b and l for later use to compute each candidate’s score (step 2 and 3). In the loop, the key step is to update M involving matrix inverse of size (l + 4)t × (l + 4)t which is relatively cheaper to compute (step 17).

The effectiveness and efficiency of TEAMREP-FAST-EXACT are summarized in Lemma 2 and Lemma 3, respectively. Compared with TEAMREP-BASIC, Algorithm 1 is much faster without losing any recommendation accuracy.

Algorithm 1.

TEAMREP-FAST-EXACT

Lemma 2

Accuracy of TEAMREP-FAST-EXACT. Algorithm 1 outputs the same set of candidates as TEAMREP-BASIC.

Proof

(Sketch) First, according to Lemma 1, we will not miss a promising candidate during the pruning stage. Second, for each candidate after pruning, Algorithm 1 calculates its graph kernel exactly the same as Eq. (5), which is in turn the same as Eq. (4) and hence Eq. (2). Therefore, after ranking the scores, Algorithm 1 outputs the same set of candidates as TEAMREP-BASIC.

Lemma 3

Time Complexity of TEAMREP-FAST-EXACT Algorithm 1 takes $O(({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i})(l{t}^5+l^3{t}^3))$ in time.

Proof

(Sketch) After pruning, the number of potential candidates (the number of loops in Algorithm 1) is $O({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i})$. In every loop, computing X₁,X₂ and Y₁ take O(lt⁵); computing M takes O(lt⁵+l³t³) and computing the score(q) takes O(lt³). Putting everything together, the time complexity of Algorithm 1 is $O(({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i})(l{t}^5+l^3{t}^3))$.

4.5.2 Variant #2: Teamrep-Fast-Approx

By using Eq. (6) to compute the graph kernel instead, we propose an even faster algorithm (TEAMREP-FAST-APPROX), which is summarized in Algorithm 2. In the algorithm, we only need to compute the top r eigen-decomposition for A_c once (step 2), and use that to update the low rank approximation for every new team. Besides, when we update M, a matrix inverse of size (r+2)² × (r+2)² (step 14), the time is independent of the team size.

Algorithm 2.

TEAMREP-FAST-APPROX

The effectiveness and efficiency of TEAMREP-FAST-APPROX are summarized in Lemma 4 and Lemma 5, respectively. Compared with TEAMREP-BASIC and TEAMREP-FAST-EXACT, Algorithm 2 is even faster; and the only place it introduces the approximation error is the low-rank approximation of A_c (step 2).

Lemma 4

Accuracy of TEAMREP-FAST-APPROX. If A_c = UΛU′ holds, Algorithm 2 outputs the same set of candidates as TEAMREP-BASIC.

Proof

(Sketch) First, according to Lemma 1, we will not miss a promising candidate during the pruning stage. Second, for each candidate after pruning, if A_c = UΛU′, we have that A_c = Â_c, A₁ = Â₁, and A₂ = Â₂. This means when we compute the approximated graph kernel using Eq. (6), the low rank approximations of A₁ and A₂ is exactly the same as original A₁ and A₂. Therefore, the scores calculated by Algorithm 2 are exactly the same as Eq. (2), hence outputting the same set of candidates. □

Lemma 5

Time Complexity of TEAMREP-FAST-APPROX Algorithm 2 takes $O(({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i})(l{t}^{2}r+r^6))$ in time.

Proof

(Sketch) After pruning, the number of potential candidates (the number of loops in Algorithm 2) is $O({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i})$. In every loop, computing T takes O(lt²r + lr²); computing M takes O(lt²r + lr⁴ + r⁶) and computing the score(q) takes O(lt² + r⁴). Putting everything together, we have that the time complexity of Algorithm 2 is $O(({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i})(l{t}^{2}r+r^6))$.

Remarks

Considering that ${\mathbf{L}}_1^j$ and ${\mathbf{L}}_2^j$ are diagonal matrices, computing M can be further reduced to O(ltr² + lr⁴ + r⁶).

4.5.3 Variant #3: TEAMREP-FAST-APPROXCORR

The algorithm for computing the approximated graph kernel with node correspondences as in Eq. (9) is summarized in Algorithm 3. Compared with TEAMREP-FAST-APPROX, the difference is that the starting and ending probabilities take form in Eq. (7), which will allow simplified computation in Eq. (8) (step 12–14).

Algorithm 3.

TEAMREP-FAST-APPROXCORR

The effectiveness and efficiency of TEAMREP-FAST-APPROXCORR are summarized in Lemma 6 and Lemma 7, respectively. Compared with TEAMREP-FAST-APPROX, Algorithm 3 is much faster and outputs the same set of candidates if the starting and ending probabilities take form in Eq. (7).

Lemma 6

Accuracy of TEAMREP-FAST-APPROXCORR. If the starting and ending probabilities take form in Eq. (7), Algorithm 3 outputs the same set of candidates as Algorithm 2.

Proof

(Sketch) Note the only difference between TEAMREP-FAST-APPROXCORR and TEAMREP-FAST-APPROX is that the starting and ending probabilities take form in Eq. (7) in TEAMREP-FAST-APPROXCORR. According to Eq. (9), the approximated graph kernel score is the same as output by Eq. (6).

Lemma 7

Time Complexity of TEAMREP-FAST-APPROXCORR Algorithm 3 takes $O(({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i})(lt{r}^2+r^6))$ in time.

Proof

(Sketch) After pruning, the number of potential candidates (the number of loops in Algorithm 3) is $O({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i})$. In every loop, computing T takes O(tl+tr²); computing M takes O(ltr² + lr⁴ + r⁶) and computing the score(q) takes O(lt² + r⁴). Putting everything together, we have that the time complexity of Algorithm 3 is $O(({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i})(lt{r}^2+r^6))$.

We summarize and compare the proposed algorithms in Table 2.

TABLE 2.

Comparison of proposed algorithms.

Algorithm	Time Complexity	Remark
TEAMREP-BASIC	O(nlr′t3)	Direct graph computations
TEAMREP-FAST-EXACT	$O\left(\left({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i}\right)(l{t}^5+l^3{t}^3)\right)$	Pruning + smoothness
TEAMREP-FAST-APPROX	$O\left(\left({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i}\right)(l{t}^{2}r+r^6)\right)$	Pruning + smoothness + low-rank approximation
TEAMREP-FAST-APPROXCORR	$O\left(\left({\displaystyle {\sum }_{i\in \mathcal{T}/p}{d}_i}\right)(lt{r}^2+r^6)\right)$	Pruning + smoothness + low-rank approximation + node correspondence

5 Beyond Team Member Replacement: Team Refinement, Team Expansion and Team Shrinkage

In this section, we discuss how the techniques for TEAM MEMBER REPLACEMENT can be applied to the other team enhancement scenarios, including TEAM REFINEMENT, TEAM EXPANSION and TEAM SHRINKAGE. We note that the fast solutions developed in Section 4 also apply to these scenarios, and thus omit the detailed discussions.

5.1 Team Refinement

In TEAM REFINEMENT, we want to edit a current team member p to have the desired skill l and communication structure vector a. As the person with the exact skill and communication requirements might not exist in the network, we aim to find a best-effort match. We define a ‘virtual member’ ν to be the person with skill l and network structure a and a ‘virtual team’ ${\mathcal{T}}^{\prime }$ to be ${\mathcal{T}}_{p\to \nu }$. Using graph kernel, the best-effort match q can be found as:

$$q={\text{argmax}}_{j,j\notin \mathcal{T}}\text{Ker(}\mathbf{G}({\mathcal{T}}^{\prime }),\mathbf{G}({{\mathcal{T}}^{\prime }}_{\nu \to j}\text{))}$$ (10)

5.2 Team Expansion

In TEAM EXPANSION, we want to add a team member with the desired skill l and communication structure vector a. Again, because the exact match might not exist, we instead find a best-effort match. We define a ‘virtual member’ ν to be the person with skill l and network structure a and a ‘virtual team’ ${\mathcal{T}}^{\prime }$to be $\{\mathcal{T},\nu \}$. Using graph kernel, the best-effort match q can be found as:

$$q={\text{argmax}}_{j,j\notin \mathcal{T}}\text{Ker(}\mathbf{G}({\mathcal{T}}^{\prime }),\mathbf{G}({{\mathcal{T}}^{\prime }}_{\nu \to j}\text{))}$$ (11)

5.3 Team Shrinkage

In TEAM SHRINKAGE, we want to remove a current team member with minimum disruption. Since graph kernel can characterize the team-level similarity, it can also be applied to TEAM SHRINKAGE. The idea is to find a current team member p so that the new team after p leaves is most similar to the old team. That is, we want to find a member $p\in \mathcal{T}$ such that:

$$p={\text{argmax}}_{j\in \mathcal{T}}\text{Ker(}\mathbf{G}(\mathcal{T}),\mathbf{G}({\mathcal{T}}_{/j}\text{))}$$ (12)

where $\mathbf{G}({\mathcal{T}}_{/j})$ is the labelled team graph after a team member j leaves. Note that in TEAM SHRINKAGE, the search space is no longer the rest network but the team itself, which is much smaller.

6 Experimental Evaluations

In this section, we present the experimental evaluations. The experiments are designed to answer the following questions:

• Effectiveness: How accurate are the proposed algorithms for TEAM ENHANCEMENT?

• Efficiency: How scalable are the proposed algorithms?

6.1 Datasets

DBLP

DBLP dataset⁴ provides bibliographic information on major computer science journals and proceedings. We use it to build a co-authorship network where each node is an author and the weight of each edge stands for the number of papers the two corresponding authors have coauthored. The network constructed has n = 916, 978 nodes and m = 3, 063, 244 edges. We use the conferences (e.g., KDD, SIGMOD, CVPR, etc) to reflect authors’ skills (e.g., data mining, data base, computer vision, etc) and for a given author and conference, we define his/her skill level as the percentage of the papers s/he publishes in that conference. For a given paper, we treat all of its co-authors as a team. Alternatively, if a set of authors co-organize an event (such as a conference), we also treat them as a team.

Movie

This dataset⁵ is an extension of MovieLens dataset, which links movies from MovieLens with their corresponding IMDb webpage and Rotten Tomatoes review system. It contains information of 10,197 movies, 95,321 actors/actress and 20 movie genres (e.g., action, comedy, horror, etc.). Each movie has on average 22.8 actors/actresses and 2.0 genres assignments. We set up the social network of the actors/actresses where each node represents one actor/actress and the weight of each edge is the number of movies the two linking actors/actresses have co-stared. We use the movie genres that a person has played as his/her skills. For a given movie, we treat all of its actors/actress as a team.

NBA

The NBA dataset⁶ contains NBA and ABA statistics from the year of 1946 to the year of 2009. It has information of 3,924 players and 100 teams season by season. We use players’ positions as their skill labels, including guard, forward and center. The edge weight of the player network stands for the number of seasons that the two corresponding nodes/individuals played in the same team.

The statistics of these three datasets are summarized in Table 3. All the experiments are run on a Windows machine with 16 GB memory and Intel i7-2760QM CPU.

TABLE 3.

Summary of Datasets.

Data	n	m	# of teams
DBLP	916,978	3,063,244	1,572,278
Movie	95,321	3,661,679	10,197
NBA	3,924	126,994	1,398

Repeatability of Experimental Results

All the three datasets are publicly available. We will release the code of the proposed algorithms through authors’ websites.

6.2 Effectiveness Results

Recall that we have two design objectives for our TEAM MEMBER REPLACEMENT problem, including both the skill match and the structural match. Our effectiveness evaluations focus on the following two aspects. First, we examine whether simultaneously considering both design objectives outperform only considering one of them. Second, we evaluate to what extent our graph kernel formulation outperforms other alternative choices, in order to fulfill both design objectives (i.e., the skill match and the structural match). To be specific, we compare to the following alternative methods, including (a) only with structure matching and not including L_× in Eq. (2) (Graph Only), (b) only with skill matching and using cosine similarity of skill vectors as scores (Skill Only), (c) computing the score from the Euclidean distance of skill vectors (Skill EuclideanDist), (d) using the weighted sum of scores by ‘Skill Only’ and ‘Graph Only’ (Linear Combination), (e) using the multiplication of the two (Multiplicative Combination), and (f) first picking those with high ‘Skill Only’ scores and then ranking them by ‘Graph Only’ scores (Sequential Filtering).

A. Qualitative Evaluations

We first present some case studies on the three datasets to gain some intuitions.

Case studies on DBLP

Let us treat the organizing committee of KDD 2013 as a team. After filtering those not in DBLP, we have 32 people in the committee team. We use their co-authorship network as their social network. Suppose one of the research track co-chairs Inderjit Dhillon becomes unavailable and we are searching for another researcher who can fill in this critical role in organizing KDD 2013. The top five candidates our algorithm recommends are in Table 4. The results are consistent with the intuitions - all of these recommended researchers are highly qualified - not only have they made remarkable contributions to the data mining field, but also they have strong ties with the remaining organizers of KDD 2013. For example, Liu is the current chair of KDD executive committee; Wang is one of the research track program chairs for KDD 2014; and Faloutsos was the PC co-chair of KDD 2003, etc. We also develop a prototype system to visualize the teams before and after replacement. For details, please refer to our conference version of the paper [5].

TABLE 4.

Case studies results

Dataset	Method	Recommendations
DBLP	Ours Graph Only Skill Only Multiplicative Combination	Philip S. Yu, Jiawei Han, Christos Faloutsos, Bing Liu and Wei Wang Jian Wu, Ada Wai-Chee Fu, Ke Wang, Heikki Mannila, Daxin Jiang W. Nick Street, Kristin P. Bennett, David Gondek, Bianca Zadrozny, Katsuhiko Takabayashi David Gondek, Katsuhiko Takabayashi, Jeremy Z. Kolter, Hung Hay Ho, Genady Grabarnik
Movie	Ours Graph Only Skill Only Multiplicative Combination	Samuel L. Jackson, Steve Buscemi, Robert De Niro, Christopher Walken, Bruce Willis Tommy Lee Jones, Woody Harrelson, Stanley Tucci, Nicky Katt, Juliette Lewis Chris Cooper, Clive Owen, Gig Young, Stellan Skarsgrd, Brad Hunt Gig Young, Brad Hunt, Adrien Brody, Danny Huston, Faye Dunaway
NBA	Ours Graph Only Skill Only Multiplicative Combination	Rick Fox, A.c. Green, Jason Kidd, Brian Shaw and Tyronn Lue Rick Fox,A.c. Green,Chucky Brown, Michael Finley, Jason Kidd Mahmo Abdul-rauf,Tariq Abdul-wahad,Forest Able,Alex Acker,Donald Ackerman Mahmo Abdul-rauf, Forest Able, Alex Acker, Donald Ackerman, Hassan Adams

Case studies on Movie

Assuming actor Matt Damon became unavailable when filming the epic war movie Saving Private Ryan (1998) and we need to find an alternative actor who can play Ryan’s role in the movie. The top five recommendations our algorithm gives are in Table 4. As we know, Saving Private Ryan is a movie of action and drama genres. Notice that both Damon and Jackson have participated in many movies of drama, thriller and action genres, hence Jackson has the acting skills required to play the role in this movie. Moreover, Jackson has co-played with Tom Sizemore, Vin Diesel, Dale Dye, Dennis Farina, Giovanni Ribisi and Ryan Hurst in the crew before. The familiarity might increase the harmony of filming the movie with others.

Case studies on NBA

Let us assume that Kobe Bryant in Los Angeles Lakers was hurt during the regular season in 1996 and a bench player is badly wanted. The top five replacements our algorithm recommends can be seen in Table 4. As we know, Bryant is a guard in NBA. Among the five recommendations, Kidd, Shaw and Lue all play as guards. More importantly, Jason, Brian and Tyronn have played with 9, 7 and 9 of the rest team members on the same team in the same season for multiple times. Therefore, it might be easier for them to maintain the moment and chemistry of the team which is critical to winning the game.

Case studies on TEAM EXPANSION

Suppose we want to expand the organizing committee of KDD 2013 by hiring a researcher with strong expertise in Artificial Intelligence, and preferably who has collaborated with as many researchers on the committee as possible. The top five candidates found by our algorithm are: Qiang Yang, Zoubin Ghahramani, Eric Horvitz, Thomas G. Dietterich and Raymond J. Mooney. All the candidates have made significant contributions to the field of artificial intelligence and Yang, Horvitz, Dietteirch and Mooney are the current AAAI fellows. Among them, Yang has collaborated with some previous KDD organizing committee members (e.g., Jian Pei, Ying Li, Geoff Webb and Dou Shen).

B. Quantitative Evaluations

Besides the above case studies, we also perform quantitative evaluations.

User studies

We perform a user study with 20 people as follows. We choose 10 papers from various fields, replace one author of each paper, run our method and the first two comparison methods, and each of them recommends top five candidates. Then, we mix the outputs (15 recommendations in total) and ask users to (a) mark exactly one best replacement; (b) mark all good replacements from the list of 15 recommended candidates. The results are presented in Fig. 1, Fig. 2 and Fig. 3, respectively. As we can see from these figures, the proposed method (the green bar) is best in terms of both precision and recall. For example, the average recalls by our method, by ‘Graph Only’ and by ‘Skill Only’ are 55%, 28%, 17%, respectively. As for different papers, our method wins 9 out of 10 cases, except for ‘paper 2′ where ‘Skill Only’ is best. One possible reason for the exception is that in ‘paper 2′ [14], all the authors are primarily in computer vision while the person leaving (Prof. Han) is mostly focused in data mining. As a result, using our method and Graph Only will bias towards those candidates in computer vision; while the recommendations made by Skill Only are more preferred by the users.

Fig. 1.

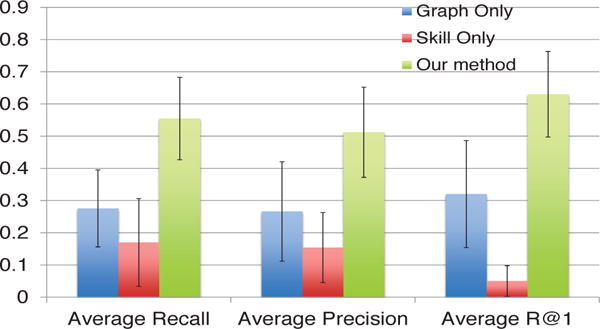
The average recall, average precision and R@1 of the three comparison methods. Higher is better.

Fig. 2.

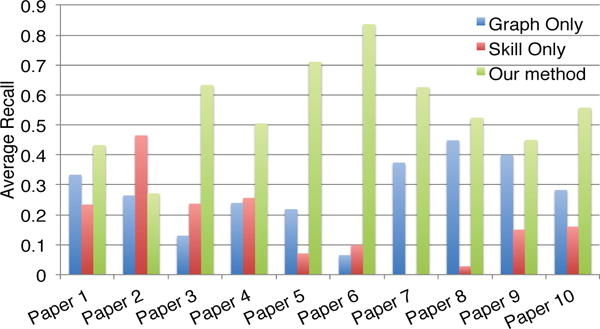
Recall for different papers. Higher is better.

Fig. 3.

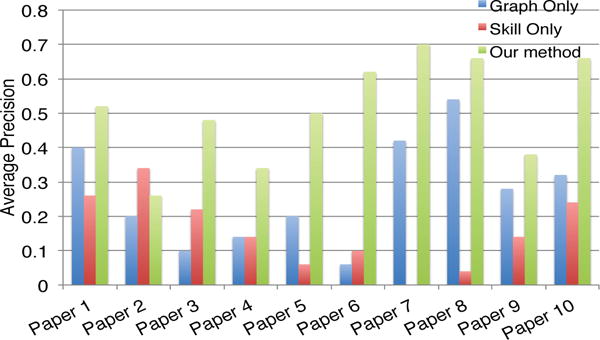
Precision for different papers. Higher is better.

Author alias prediction

In DBLP, some researchers might have multiple name identities/alias. For example, in some papers, Alexander J. Smola might be listed as Alex J. Smola, Zhongfei (Mark) Zhang might be listed as Zhongfei Zhang, etc. For such an author, we run the team replacement algorithm on those papers s/he was involved to find top-k replacement. If his/her other alias appears in the top-k recommended list, we treat it as a hit. The average accuracy of different methods is shown in Fig. 4. Again, our method performs best. It outperforms both the methods that consider only one design objective (‘Skill Only’, ‘Graph Only’ and ‘Skill EuclideanDist’); and also those that use alternative ad-hoc methods to combine both skill and structural match (‘linear combination’, ‘multiplicative combination’ and ‘sequential filtering’).

Fig. 4.

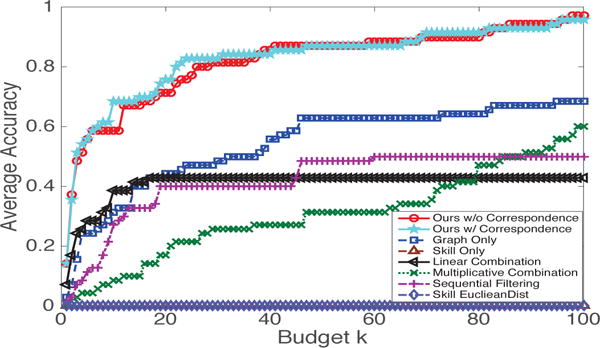
Average accuracy vs. budget k. Higher is better.

Team Shrinkage

In DBLP, we select teams with over 10 members and manually inject a “noisy” individual to the team such that the individual is connected with all the team members with random edge weights and has randomly generated skill vectors. Recall that, in team shrinkage we want to find the “best” member to leave the team without much disruption to the team. In our setting, we treat the “noisy” individual as the “best” candidate. For “Skill Only”, we first compute the similarity matrix among all team members using inner product of their skill vectors and then apply max-pooling as their score. Figure 6 shows the result of our method, “Graph Only” as well as “Skill Only”. Our method achieves the best Precision@1, Recall@1 and F@1.

Fig. 6.

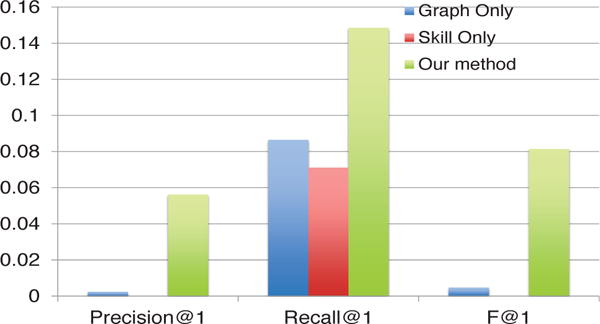
Precision@1, Recall@1 and F@1 of the three comparison methods for TEAM SHRINKAGE. Higher is better.

6.3 Efficiency Results

A. The speed-up by pruning

To demonstrate the benefit of our pruning strategy, we run TEAMREP-BASIC with and without pruning on the three datasets and compare their running time. For DBLP, we choose the authors of paper [15] (6 authors); for Movie, we select the film crew of Titanic (1997) (22 actors/actresses); for NBA, we pick the players on the Los Angeles Lakers in year 1996 (17 players). The result is presented in Fig. 5. As we can see, the pruning step itself brings significant savings in terms of running time, especially for larger graphs (e.g., DBLP and Movie). Notice that according to Lemma 1, we do not sacrifice any recommendation accuracy by pruning.

Fig. 5.

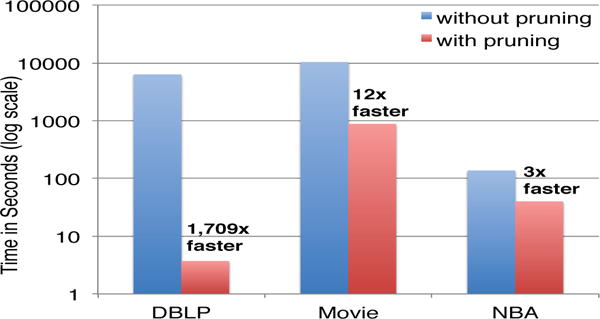
Time Comparisons before and after pruning on three datasets. Notice time is in log-scale.

B. Further speedup

Next, we vary the team sizes and compare the running time of TEAMREP-BASIC with TEAMREP-FAST-EXACT(exact methods); and Ark-L [12] with TEAMREP-FAST-APPROX and TEAMREP-FAST-APPROXCORR(approximate methods). For TEAMREP-BASIC and Ark-L, we apply the same pruning step as their pre-processing step. The results on DBLP are presented in Fig. 7 and Fig. 8, respectively. We can see that the proposed TEAMREP-FAST-EXACT and TEAMREP-FAST-APPROX are much faster than their alternative choices, especially when team size is large. Besides, knowing the node correspondences, TEAMREP-FAST-APPROXCORR can achieve additional speed-up compared to TEAMREP-FAST-APPROX. No tice that Ark-L is the best known method for approximating random walk based graph kernel.

Fig. 7.

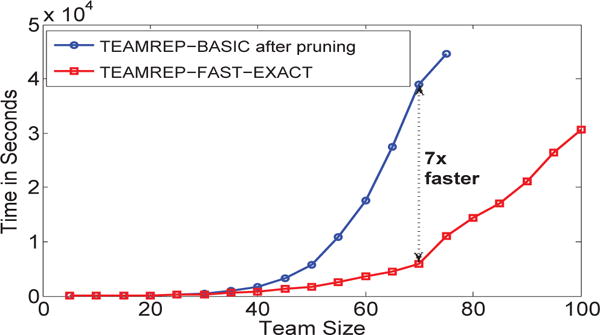
Time Comparison between TEAMREP-BASIC and TEAMREP-FAST-EXACT. TEAMREP-FAST-EXACT is on average 3× faster. TEAMREP-BASIC takes more than 10 hours when team size = 70.

Fig. 8.

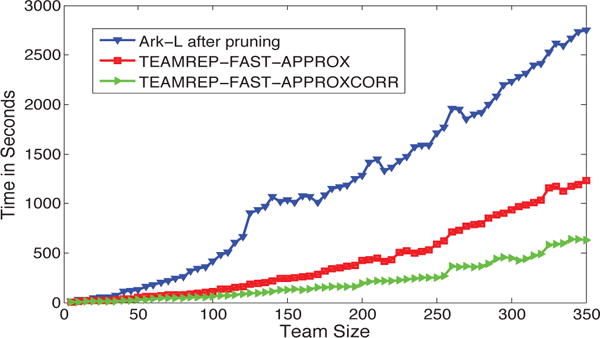
Time Comparisons between Ark-L[20] and TEAMREP-FAST-APPROX, TEAMREP-FAST-APPROXCORR.

C. Scalability

To test the scalability of our TEAMREP-FAST-EXACT, TEAMREP-FAST-APPROX and TEAMREP-FAST-APPROXCORR algorithms, we sample a certain percentage of edges from the entire DBLP network and run the two proposed algorithms on teams with different sizes. The results are presented in Fig. 9, Fig. 10 and Fig. 11, respectively. As we can seen, all algorithms enjoy a sub-linear scalability w.r.t. the total number of edges of the input graph (m).

Fig. 9.

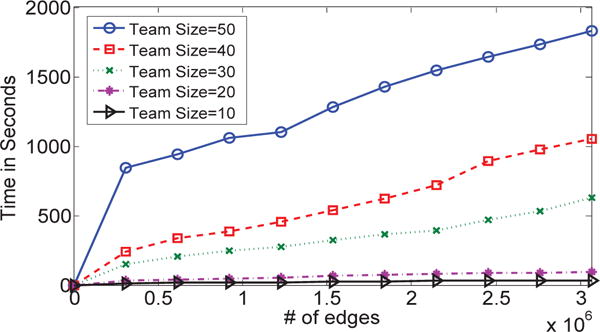
Running time of TEAMREP-FAST-EXACT vs. graph size. TEAMREP-FAST-EXACT scales sub-linearly w.r.t. the number of edges of the input graph.

Fig. 10.

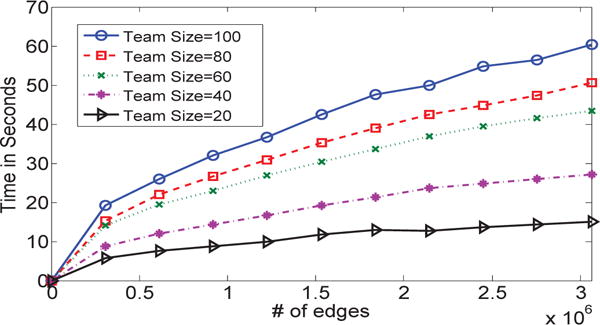
Running time vs. graph size. TEAMREP-FAST-APPROX scales sub-linearly w.r.t. the number of edges of the input graph.

Fig. 11.

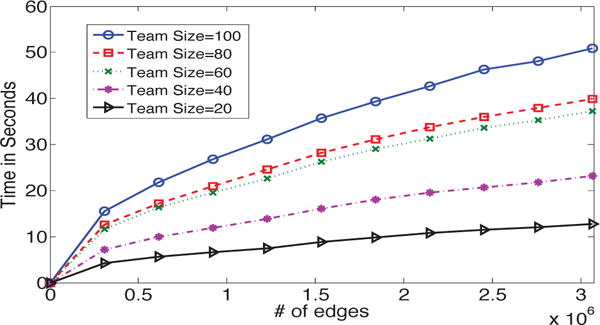
Running time vs. graph size. TEAMREP-FAST-APPROXCORR scales sub-linearly w.r.t. the number of edges of the input graph.

7 Related Work

In this section, we review the related work in terms of (a) team formation, (b) recommendation and expert finding, and (c) graph kernel.

Team Formation

Team formation studies the problem of assembling a team of people to work on a project. To ensure success, the selected team members should possess the desired skills and have strong team cohesion, which is first studied in [2]. As follow-up work, Anagnostopoulos et al [3] studies forming teams to accommodate a sequence of tasks arriving in an online fashion and Rangapuram et al [4] allows incorporating many realistic requirements into team formation based on a generalization of the densest subgraph problem. With the presence of the underlying social network, the set cover problem is complicated by the goal of lowering the communication cost at the same time. Cao et al [16] develop an interactive group mining system that allows users to efficiently explore the network data and from which to progressively select and replace candidate members to form a team. Bogdanov et al [17] studies how to extract a diversified group pulled from strong cliques given a network; this ensures that the group is both comprehensive and representative of the whole network. Cummings and Kiesler [8] find that prior working experience is the best predictor of collaborative tie strength. To provide insights into designs of online communities and organizations, the systematic differences in appropriating social softwares among different online enterprise communities is analyzed in [18]. The patterns of informal networks and communication in distributed global software teams using social network analysis is also investigated in [19]. Specific communication structures are proven critical to new product development delivery performance and quality [9]. To assess the skills of players and teams in online multi-player games and team-based sports, “team chemistry” is also accounted for in [20, 21]. Along another line, recently some work aim at predicting the long term performance of a team [22, 23].

Recommendation and Expert Finding

Recommendation and expert finding is a very active research topic in data mining and information retrieval, either to recommend products a user is mostly interested in or to identify the most knowledgeable people in a field. Our work is related to this in the sense that we aim to recommend top candidates who are most suitable for the vacancy. A popular method in recommendation (collaborative filtering) is latent factor model [24, 25, 26]. The basic idea is to apply matrix factorization to user-item rating data to identify the latent factors. The factorization technique can be naturally extended by adding biases, temporal dynamics and varying confidence levels. In question-answering sites, e.g., Quora and Stack Overflow, an important task is to route a newly posted question to the ‘right’ user with appropriate expertise and several methods based on link analysis have been proposed [27, 28, 29]. In academia, identifying experts in a research field is of great value, e.g., assigning papers to the right reviewers in a peer-review process [30, 31], which can be done by either building the co-author network [15] or using language model and topic-based model [32, 33]. For enterprises, finding the desired specialist can greatly reduce costs and facilitate the ongoing projects. Many methods have been proposed to expert search through an organization’s document repository [34, 35].

Graph Kernel

Graph kernel measures the similarity between two graphs. Typical applications include automated reasoning [36], bioinformatics/chemoinformatics [37, 38]. Generally speaking, graph kernels can be categorized into three classes: kernels based on walks [10, 11, 39, 40, 41], kernels based on limited-sized subgraphs [42, 43, 44] and kernels based on subtree patterns [45, 46, 47]. Graph kernels based on random walk is one of the most successful choices [48]. The idea is to perform simultaneous walks on the two graphs and count the number of matching walks. One challenge of random walk based graph kernel lies in computation. The straight-forward method for labelled graphs take O(lr′t³) time by reducing to the problem of solving a linear system [10, 11]. With low rank approximation, the computation can be further accelerated with high approximation accuracy [12].

8 Conclusion

In this paper, we study a family of problems under the umbrella of TEAM ENHANCEMENT, namely, TEAM MEMBER REPLACEMENT, TEAM REFINEMENT, TEAM EXPANSION and TEAM SHRINKAGE. To our best knowledge, we are the first to study these problems related to teams in large-scale networks. The basic idea of our method is to adopt graph kernel to encode both skill matching and structural matching. To address the computational challenges, we propose a suite of fast and scalable algorithms. Extensive experiments on real world datasets validate the effectiveness and efficiency of our algorithms. To be specific, (a) by bringing skill matching and structural matching together, our method is significantly better than the alternative choices in terms of both average precision (24% better) and recall (27% better); and (b) our fast algorithms are orders of magnitude faster while enjoying a sub-linear scalability.

This paper has presented an efficient technique in addressing the team enhancement challenge; however, the proposed method can be applied to general graph mining problem where the interaction of multiple objectives is critical, e.g., finding a similar multimedia object by considering both its content and relationship with other objects. In the future, we would like to expand team enhancement to team composition. For instance, given the structure of a high-grossing movie (e.g., Saving Private Ryan) of a particular genre, we want to develop an effective algorithm to suggest a team of actors.

Biographies

Liangyue Li is a Ph.D. student at School of Computing, Informatics and Decision System Engineering at Arizona State University. He received the B.Eng. degree in Computer Science from Tongji University in 2011. His current research interests include large scale data mining and machine learning, especially for large graph data with application to social network analysis.

Hanghang Tong is currently an assistant professor at School of Computing, Informatics and Decision Systems Engineering at Arizona State University. Before that, he was an assistant professor at Computer Science Department, City College, City University of New York, a research staff member at IBM T.J. Watson Research Center and a Post-doctoral fellow in Carnegie Mellon University. He received his M.Sc and Ph.D. degree from Carnegie Mellon University in 2008 and 2009, both majored in Machine Learning. His research interest is in large scale data mining for graphs and multimedia. He has received several awards, including best paper award in CIKM 2012, best paper award in SDM 2008 and best research paper award in ICDM 2006. He has published over 100 referred articles and more than 20 patents. He has served as a program committee member in top data mining, databases and artificial intelligence venues (e.g., SIGKDD, SIGMOD, AAAI, WWW, CIKM, etc).

Nan Cao is a Research Staff Member at IBM T. J. Watson Research Center. His research interests include data visualization and visual analysis. He creates novel visualizations for representing complex (i.e., big, dynamic, multivariate, heterogeneous, and multirelational) graph data in the domains of social science and medical informatics.

Kate Ehrlich is a Senior Technical Staff Member in the Cognitive User Experience Lab at IBM Research where she uses Social Network Analysis (SNA) and other methods to gain insights into patterns of collaboration, information flow and decision-making in teams and communities that lead to recommendations and analytics for improved performance. Kate has published academic papers on her research in CHI, CSCW, software engineering and management science premier conferences and journals. Kate has a B.Sc in Psychology from the University of London and a PhD. in Cognitive Science from the University of Sussex, UK. She did post-doctorate work in cognitive science at University of Texas, University of Massachusetts and Yale. Kate has been active in the ACM SIG on Human Computer Interaction including founder of the Boston chapter and co-chair of the CSCW conference. She has co-chaired other professional and business conferences and she serves on the review committees of conferences and journals in CHI, CSCW and software engineering.

Yu-Ru Lin is an assistant professor at the School of Information Sciences, University of Pittsburgh. Her research interests include human mobility, social and political network dynamics, and computational social science. She has developed computational approaches for mining and visualizing large-scale, time-varying, heterogeneous, multi-relational, and semi-structured data.

Norbou Buchler is a cognitive scientist in the Human Research & Engineering Directorate of the Army Research Laboratory. His basic research interests lie in understanding human cognition and decision-making at network levels of interaction using multi-disciplinary approaches including social network analysis, cognitive modeling, multi-agent simulation, and behavioral laboratory experimentation. His applied research focuses on human system integration and developing agent-based decision-support technologies for application in both cybersecurity and Mission Command environments. Norbou received his Ph.D. in experimental psychology from Syracuse University, and did two post-doctoral fellowships, first at Carnegie Mellon University examining computational and behavioral approaches to cognition, and second at the Center for Cognitive Neuroscience at Duke University.