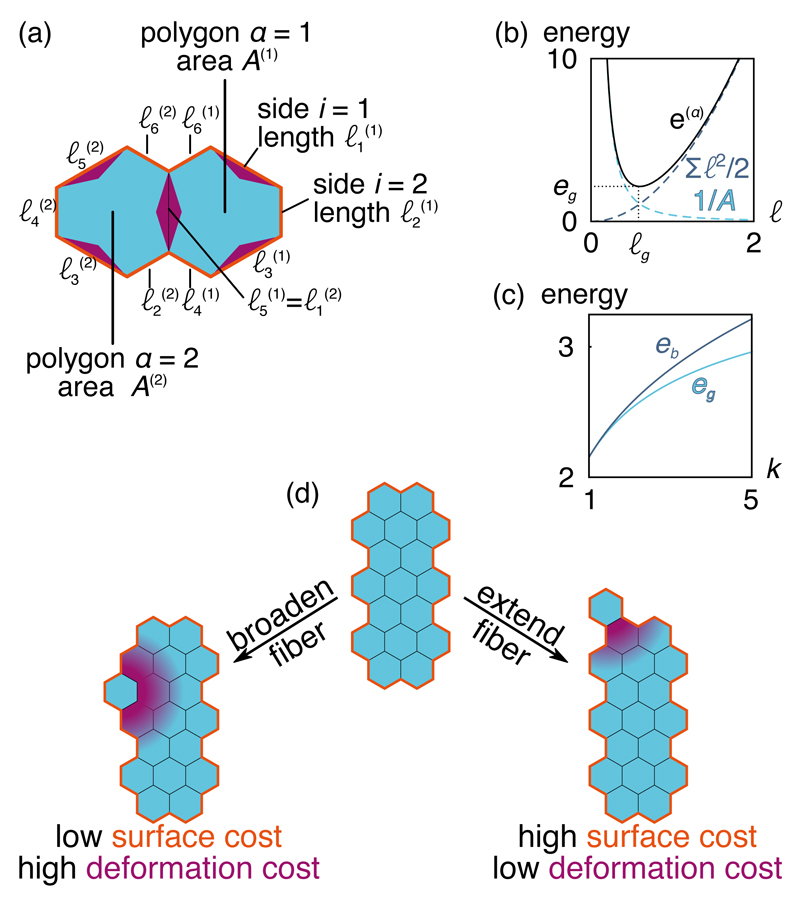
Figure 2. Polygon model of aggregation.

Here we present hexagons with sides of alternating length characterized by an asymmetry parameter k > 1. (a) Two-hexagon aggregate with two joined sides and 10 unjoined sides outlined in orange. (b) Magnitude of the total energy e^(α) of a k = 1 regular hexagon of side ℓ. We also plot separately each of its two terms as defined in the Methods. The equilibrium side length ℓ_g and ground-state deformation energy e_g are shown. (c) Hexagons with alternating sides become increasingly frustrated as their asymmetry is increased (k ≠ 1), as evidenced by the increasing gap between the energies of the ground state (e_g) and the bulk [e_b, corresponding to the bulk topology of Fig. 1(c)]. This frustration eventually decreases at high k as the hexagon bulk goes to a triangular lattice (see Supplementary information). (d) Two contrasting additions to an anisotropic aggregate: left, to a side flank that broadens the fiber, right, to the end of the fiber to extend it. The different energy costs are noted below each case, and illustrated on the figure by the orange line and the purple shading, respectively.