Tracking the Same Neurons across Multiple Days in Ca²⁺ Imaging Data

Summary

Ca²⁺ imaging techniques permit time-lapse recordings of neuronal activity from large populations over weeks. However, without identifying the same neurons across imaging sessions (cell registration), longitudinal analysis of the neural code is restricted to population-level statistics. Accurate cell registration becomes challenging with increased numbers of cells, sessions, and inter-session intervals. Current cell registration practices, whether manual or automatic, do not quantitatively evaluate registration accuracy, possibly leading to data misinterpretation. We developed a probabilistic method that automatically registers cells across multiple sessions and estimates the registration confidence for each registered cell. Using large-scale Ca²⁺ imaging data recorded over weeks from the hippocampus and cortex of freely behaving mice, we show that our method performs more accurate registration than previously used routines, yielding estimated error rates <5%, and that the registration is scalable for many sessions. Thus, our method allows reliable longitudinal analysis of the same neurons over long time periods.

Graphical Abstract

Highlights

• •A method for tracking neurons across days (cell registration) in Ca²⁺ imaging data
• •The method is probabilistic and quantitatively evaluates registration accuracy
• •The method is applicable to various imaging techniques and cell detection algorithms
• •Registration accuracy remains high with an increased number of registered sessions

Sheintuch et al. present a probabilistic method for tracking the same neurons across multiple days (cell registration) in large-scale Ca²⁺ imaging data recorded from behaving mice. The probabilities for pairs of neighboring cells from different sessions to be the same neuron are estimated and utilized to perform reliable cell registration.

Introduction

Recent advances in optical imaging techniques and genetically encoded Ca²⁺ indicators allow researchers to chronically record the activity of hundreds to thousands of neurons simultaneously in behaving animals (Svoboda et al., 1997, Helmchen et al., 2001, Sawinski et al., 2009, Ghosh et al., 2011, Grienberger and Konnerth, 2012, Chen et al., 2013). This is typically done using two-photon imaging in head-fixed rodents (Dombeck et al., 2007, Dombeck et al., 2010, Kitamura et al., 2015, Burgess et al., 2016) or one-photon imaging with miniature microscopes in freely behaving rodents (Ziv et al., 2013, Berdyyeva et al., 2014, Jennings et al., 2015, Pinto and Dan, 2015, Sun et al., 2015, Cai et al., 2016). These techniques facilitate within-subject analyses that quantify changes in neuronal activity under different experimental conditions and over extended periods of time (reviewed in Ziv and Ghosh, 2015). However, without identifying the same individual neurons across imaging sessions, the analysis of time-lapse imaging data becomes limited to population-level statistics, thus losing a critical advantage offered by optical imaging relative to dense electrophysiological recordings. Following the activity of the same neurons over time can uncover the changes in the coding properties of individual cells and in the joint activity patterns that underlie the population-level statistics (Huber et al., 2012, Ziv et al., 2013, Lütcke et al., 2013, Jennings et al., 2015, Rubin et al., 2015, Burgess et al., 2016, Cai et al., 2016, Liberti et al., 2016, Rose et al., 2016, Driscoll et al., 2017, Grewe et al., 2017). Such accounts of long-term dynamics are crucially absent in many fields of neuroscience, including the study of learning and long-term memory, where understanding how information is represented, stored, and changes with time is key.

To longitudinally follow the activity of individual neurons, the same cells need to be reliably identified (registered) across all time points in the experiment. Registration of the same neurons becomes challenging as the number of detected cells in a session, the number of sessions, and the intervals between them increase. Cell registration is further complicated in data from one-photon Ca²⁺ imaging, in comparison to two-photon imaging, due to light scattering and lack of optical sectioning (Wilt et al., 2009, Yang and Yuste, 2017), both of which increase the crosstalk between the signals of neighboring neurons in the two-dimensional field of view (FOV). Furthermore, since one-photon microscopy mostly reveals transient and localized changes in fluorescence that exceed the background noise, a cell must be active to be detected. Thus, the set of detected cells can differ between sessions (Ziv et al., 2013, Resendez et al., 2016, Grewe et al., 2017, Xia et al., 2017), and a one-to-one mapping of neural identity across sessions is typically not attainable. Taken together, these factors introduce uncertainty and, consequently, potential errors to the cell registration procedure.

While numerous methods for detecting cells and extracting their activity from Ca²⁺ imaging data have been developed (Reidl et al., 2007, Vogelstein et al., 2009, Vogelstein et al., 2010, Mukamel et al., 2009, Grewe et al., 2010, Smith and Häusser, 2010, Oñativia et al., 2013, Pachitariu et al., 2013, Maruyama et al., 2014, Pnevmatikakis et al., 2016, Theis et al., 2016), relatively little effort has been devoted to the issue of cell registration across sessions. Previous studies that registered cells across sessions (Ziv et al., 2013, Jennings et al., 2015, Rubin et al., 2015, Cai et al., 2016, Liberti et al., 2016, Kitamura et al., 2017), regardless of whether using manual or automatic routines, did not provide a quantitative evaluation of registration accuracy in terms of false-positive errors (different cells falsely registered as the same cells) and false-negative errors (the same cells falsely registered as different cells). The lack of such quantitative evaluation could be detrimental in cases where the acquired data are inadequate for longitudinal analysis and may lead to misinterpretation of the data (Harris et al., 2016). For example, either falsely identifying two different cells as the same or falsely identifying the same cell as two different cells can lead to false conclusions about the dynamics of the neuronal activity. Moreover, previous work has used fixed registration decision parameters (e.g., distance threshold), which were not optimized to the specific data.

To address these problems, we adopted a probabilistic approach to devise a method for automated cell registration across sessions. By modeling the distribution of similarities between neighboring cells across sessions, our method estimates the confidence of registration associated with each cell in the data. Moreover, it estimates the overall rates of false-positive and false-negative errors for different registration decision parameters. This approach enables cell registration that is adaptive and optimized to different datasets. Applying our method to data recorded from the hippocampus and cortex of behaving mice, we show that the same cells can be tracked over multiple weeks with estimated false-positive and false-negative rates <5%, yielding more accurate registration than the routines utilized in previous studies. Moreover, we find that registration accuracy remains high with increased numbers of sessions, demonstrating the method’s suitability for longitudinal studies. We provide an open source MATLAB code for cell registration that implements the approach presented in this paper (see Experimental Procedures).

Results

Cells Maintain Their Spatial Footprints across Multiple Days of Imaging

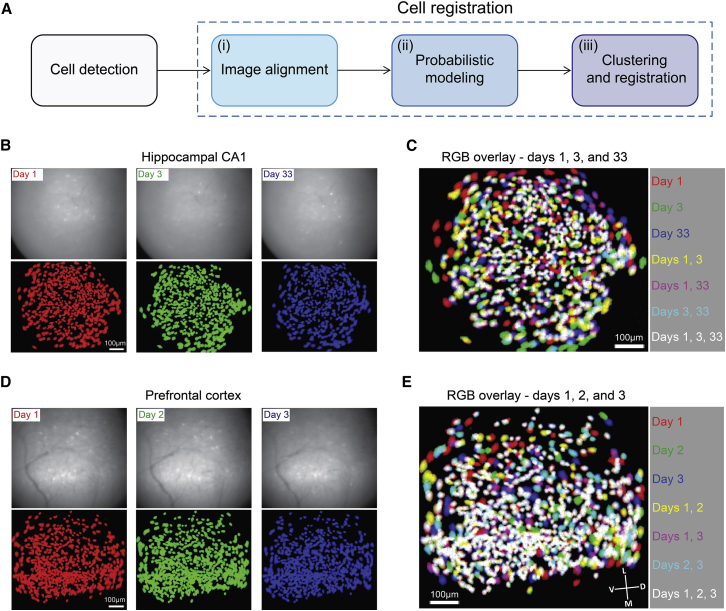
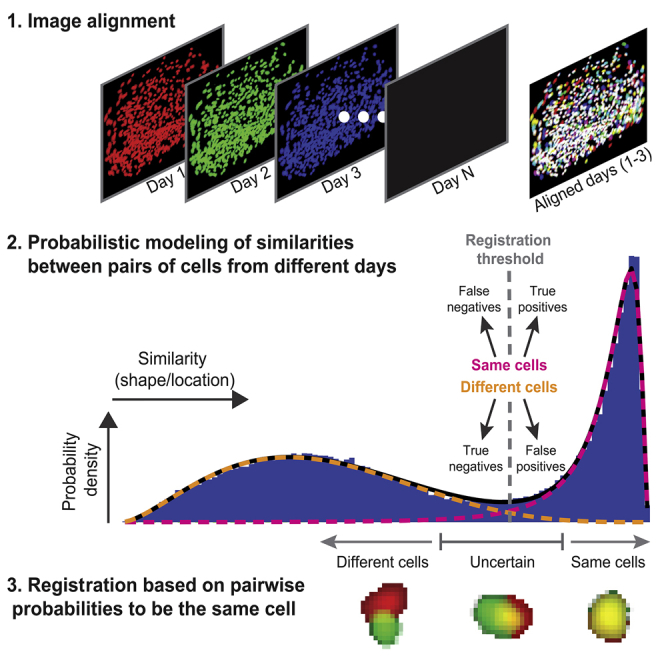
We combined miniaturized head-mounted microscopes (Ghosh et al., 2011) and microendoscopic probes (Barretto et al., 2011) to chronically image Ca²⁺ dynamics in GCaMP6-expressing neurons in the hippocampal CA1 and in the prefrontal cortex of freely behaving mice. For each mouse, we imaged Ca²⁺ dynamics in multiple recording sessions over weeks (12 mice, 6–16 sessions per mouse, 269–712 cells per session). Prior to cell registration, cells that were active in each imaging session were detected, and their spatial footprints (i.e., weighted regions of interest consisting of each pixel’s contribution to the cell’s fluorescence) and Ca²⁺ traces were extracted (Figure S1) using an established routine based on principal-component analysis and independent-component analysis (PCA-ICA; Mukamel et al., 2009). To register cells across the different sessions, we constructed a cell registration method that consists of three main steps (Figure 1A): (1) aligning between the FOVs imaged in different sessions; (2) modeling the distribution of similarities between pairs of neighboring cells from different sessions to obtain an estimation for their probability to be the same cell; and (3) registering cells across multiple sessions via a clustering procedure that uses the obtained probabilities of neighboring cell-pairs to be the same cell.

Figure 1.

Cells Maintain Their Locations and Shapes over Weeks

(A–E) In (A), the main steps in the cell registration procedure are indicated. (B and D) Top: representative single frames from raw fluorescence data of imaging sessions recorded on three different days. Bottom: projection of all spatial footprints for the same three sessions, indicated in red, green, and blue. (B) Hippocampal CA1. (D) Prefrontal cortex. (C and E) Overlays of the aligned spatial footprint maps shown for (C) hippocampal CA1, as shown in (B), and for (E) prefrontal cortex, as shown in (D). D, dorsal; L, lateral; M, medial; V, ventral. Data were recorded in the hippocampal CA1 of a Thy1-GCaMP6f transgenic mouse (B and C) and in the prefrontal cortex of a CaMKII-GCaMP6s transgenic mouse (D and E) while freely exploring the same environments.

See also Figures S1 and S2.

To correct for translation and rotation differences between sessions, we aligned the FOV of each session with the FOV of a reference session, yielding the locations of spatial footprints from different sessions in a single coordinate system (Figures 1B–1E and S2). The cells generally maintained their spatial footprints over long time periods, as indicated by the overlap of spatial footprints across sessions.

Spatial Footprint Similarities across Sessions Exhibit a Bimodal Distribution

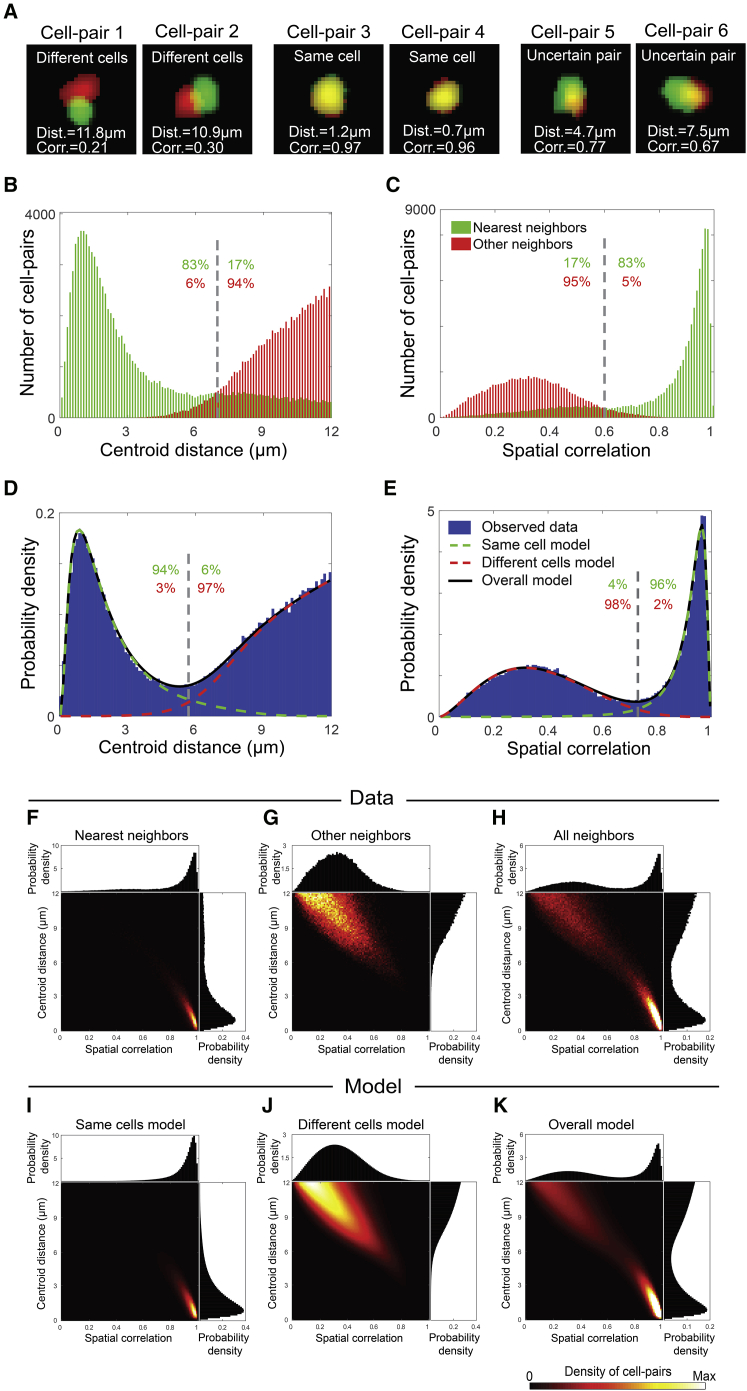
We considered all pairs of cells that were detected in close proximity in the FOV across different sessions (neighboring cell-pairs) to be same cell candidates. For each neighboring cell-pair, we measured: (1) the distance between the centers of mass of their spatial footprints (centroid distance) and (2) the Pearson correlation between their spatial footprints (spatial correlation). While some of the neighboring cell-pairs had either large centroid distances and small spatial correlations (suggesting that they are different cells) or small centroid distances and large spatial correlations (suggesting that they are the same cells), for other cell-pairs, intermediate values were observed, indicating that their registration was uncertain (Figure 2A). Therefore, we sought to register cells across sessions while obtaining a quantitative estimation of registration confidence. We limited the analysis to cell-pairs with centroid distances <12 μm, assuming that cell-pairs with larger centroid distances are different cells. We then calculated the distributions of centroid distances and spatial correlations between nearest neighbors and between other (not nearest) neighbors across sessions (Figures 2B, 2C, and S3). Based on data from 12 mice, 87% ± 3% of the nearest neighbors had a centroid distance <7 μm, and 89% ± 4% had a spatial correlation >0.6, while only 5% ± 1% of the other neighbors had a centroid distance <7 μm, and 6% ± 2% had a spatial correlation >0.6. The differences between the distributions for nearest neighbors and other neighbors support the notion that nearest neighbors are mostly the same cells, while other neighbors are, for the most part, different cells. However, registering all pairs of nearest neighbors as the same cells would result in false-positives when a cell is active in only one of the two sessions, as indicated by the heavy tail in the distributions for nearest neighbors. Furthermore, since the distributions for nearest neighbors and other neighbors partially overlap, any registration threshold, i.e., a value that serves as a cutoff for deciding whether two cells are the same, would result in false-positive errors, false-negative errors, or both.

Figure 2.

Distributions of Spatial Footprint Similarities Modeled as a Weighted Sum of Two Subpopulations

(A) Six examples of candidates to be the same cell, with their measured centroid distances (Dist.) and spatial correlations (Corr.). The spatial footprints are shown in red (session 1) and green (session 2).

(B and C) Distribution of centroid distances (B) and spatial correlations (C) between pairs of nearest neighbors (green) and other neighbors (red) across sessions. Gray dashed lines show the intersection between the two distributions. The fraction of nearest neighbors (green) or other neighbors (red) above and below these intersections are indicated.

(D and E) Distributions of centroid distances (D) and spatial correlations (E) between all neighboring cell-pairs (blue bars) and the modeled distributions of same cells (dashed green curves), different cells (dashed red curves), and their weighted sum (solid black curves). Gray dashed lines show the intersection between the two models. Estimated fractions of same cells (green) or different cells (red) above and below these intersections are indicated.

(F–H) Joint and marginal distributions of centroid distances and spatial correlations between pairs of nearest neighbors (F), other neighbors (G), and all neighbors (H) across sessions.

(I–K) Modeled joint and marginal distributions of centroid distances and spatial correlations for same cells (I), different cells (J), and their weighted sum (K). In (H) and (K), the color scale was set to reach 0.25 of the maximal value to enable visualization of both subpopulations. Data and models in all panels are for 16 sessions recorded on 8 different days in the hippocampal CA1 of a mouse while freely exploring the same environments.

See also Figures S3, S4, S5, and S6.

To estimate the attainable accuracy of cell registration, we calculated the distributions of centroid distances and spatial correlations between all (nearest and other) neighboring cell-pairs from different sessions (Figures 2D and 2E). Both distributions were bimodal, reflecting the fact that they comprise two different subpopulations of cell-pairs corresponding to same cells and different cells. Therefore, we modeled the data (centroid distances model and spatial correlations model) as a weighted sum of the distributions of two subpopulations. For each mouse, we jointly estimated the parameters of the distributions of the two subpopulations and their weights to best fit the data (Figures 2D, 2E, and S4A–S4F, showing additional examples for mice imaged in the prefrontal cortex or hippocampus). The obtained estimated distributions enable an informed choice of the registration threshold that is optimized to the data of each mouse (Figures 2D and 2E, gray dashed lines at the intersection of the two distributions; Figures S4G and S4H). Similarly, we used the joint distribution of centroid distances and spatial correlations across sessions to model the data (joint model; Figures 2F–2K, S5, and S6).

A Large Fraction of Cell-Pairs Can Be Reliably Registered across Sessions

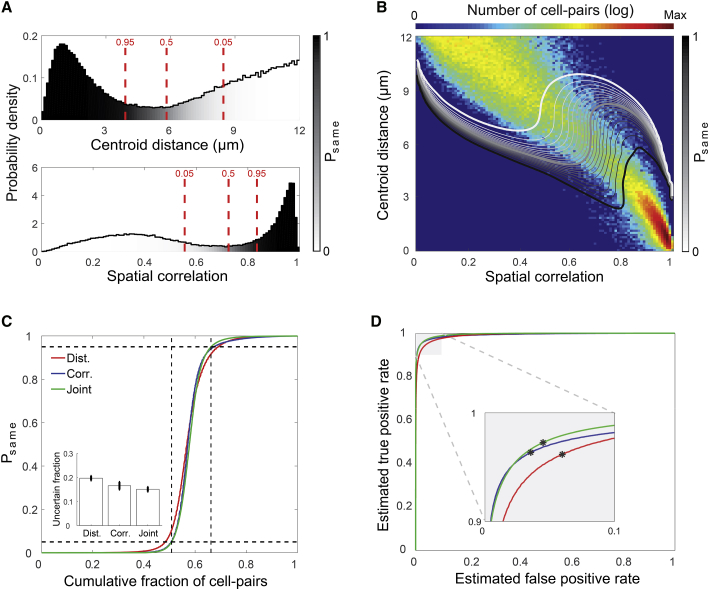
The resulting models allowed us to use a Bayesian framework to calculate the probability for two cells from two different sessions to be the same cell (P_same), given their spatial correlation and centroid distance (Figures 3A and 3B). By applying P_same (calculated for each mouse individually) to the distribution of cell-pairs in our data (802,862 neighboring cell-pairs pooled from 12 mice), we obtained the cumulative fraction of cell-pairs as a function of P_same (Figure 3C). We defined uncertain registrations of cell-pairs as those with a probability ≤0.95 to be the same cells and a probability ≤0.95 to be different cells (0.05 ≤ P_same ≤ 0.95) and found that the spatial correlations and joint models result in less uncertainty than the centroid distances model (inset of Figure 3C; 19.7% ± 3.3%, 16.6% ± 5.5%, and 15.1% ± 3.4% of the neighboring cell-pairs are in the uncertain range for the centroid distances, spatial correlations, and joint models, respectively; one-way repeated-measures ANOVA, F(1, 16) = 11.6, p = 0.002). Additionally, we used the estimated probability distributions of same cells and different cells to calculate a receiver operating characteristic (ROC) curve, providing the estimated false-positive and false-negative rates for various registration thresholds (Figure 3D). We calculated the Gini coefficient G₁ (a measure for the area under the curve) and found that the joint model performs slightly better than the centroid distances and spatial correlations models (G₁ = 0.983 ± 0.005, G₁ = 0.986 ± 0.008, and G₁ = 0.991 ± 0.004 for the centroid distances, spatial correlations, and joint models, respectively; one-way repeated-measures ANOVA, F(1, 16) = 13.8, p = 0.001). For a threshold of P_same = 0.5 (see black asterisks in the inset of Figure 3D), the false-negative rates were lower for the joint model (2.7% ± 0.9%) compared to the spatial correlations and the centroid distances models (3.7% ± 1.1% and 3.8% ± 1.1%, respectively; one-way repeated-measures ANOVA, F(1, 14) = 10.9, p = 0.003), while the false-positive rates were lower for the spatial correlations model (3.6% ± 1.6%) compared to the centroid distances and joint models (6.0% ± 2.3% and 4.5% ± 1.9%, respectively; one-way repeated-measures ANOVA, F(2, 19) = 28.4, p < 0.001). Overall, these results demonstrate that accurate registration across sessions can be obtained in >95% of neighboring cell-pairs based on any of the three models.

Figure 3.

Modeling the Data Supports Reliable Cell Registration across Pairs of Sessions

(A and B) Shown in (A): distributions of centroid distances (top) and spatial correlations (bottom) between neighboring cell-pairs. The grayscale color code indicates the probability for two cells from two different sessions to be the same cell (P_same). Red lines show P_same = 0.05, P_same = 0.5, and P_same = 0.95. (B) Contours of P_same overlaid on the joint distribution of centroid distances and spatial correlations for neighboring cell-pairs. Numbers of cell-pairs are displayed in a logarithmic scale. The P_same = 0.05, P_same = 0.5, and P_same = 0.95 contours are highlighted by thicker white, gray, and black curves, respectively. Data in (A) and (B) are the same as in Figure 2.

(C and D) Shown in (C): the cumulative fraction of cell-pairs as a function of the estimated P_same for the centroid distances (red), spatial correlations (blue), and joint (green) models. Black dashed horizontal lines represent the P_same = 0.05 and P_same = 0.95 levels, while the vertical lines show the joint model’s intersection with those probabilities, indicating the fraction of uncertain registrations. Inset: the fraction of cell-pairs in the uncertain registration range (mean ± SEM). (D) Estimated ROC curves for the centroid distances (red), spatial correlations (blue), and joint (green) models. Inset: zoom-in on the near-optimal part of the ROC. Black asterisks represent the P_same = 0.5 threshold. Data in (C) and (D) were pooled from 12 mice.

Probabilistic Approach for Cell Registration Is Applicable to Different Types of Data

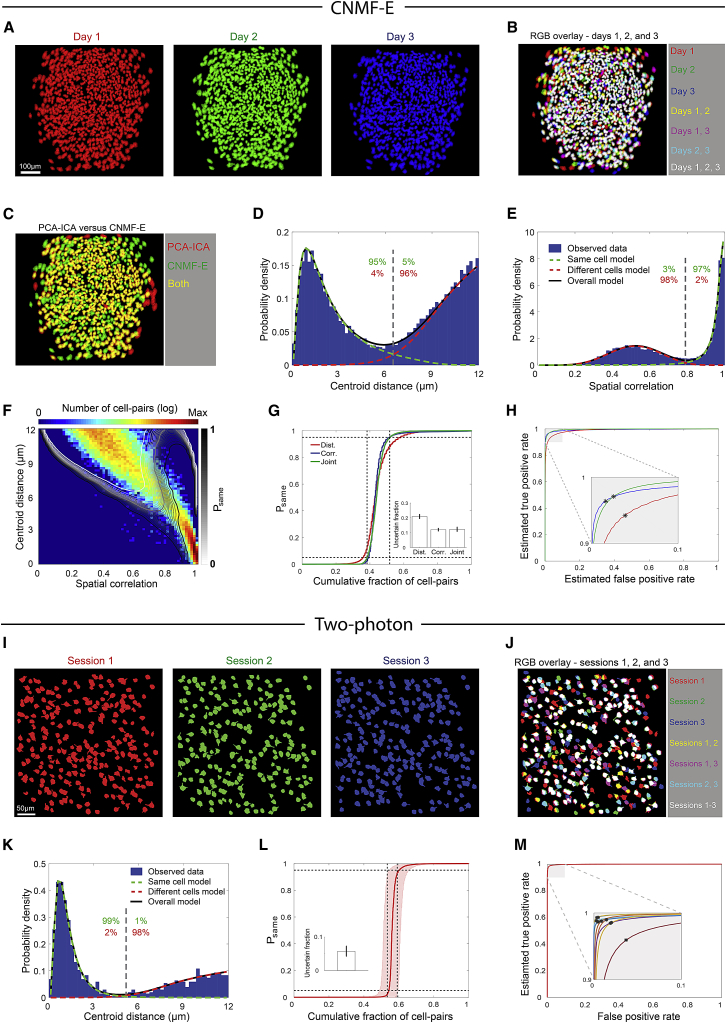
It has recently been shown that constrained nonnegative matrix factorization (CNMF) is well suited for extracting cellular spatial footprints and temporal dynamics from Ca²⁺ imaging data with significant spatial overlap between neighboring neural components (Pnevmatikakis et al., 2016). Therefore, in addition to the commonly used PCA-ICA method, we also used CNMF-E (Zhou et al., 2016), an extension of the CNMF method for one-photon microendoscopic data (Figures 4A and 4B). Notably, using CNMF-E, we detected within the same FOVs 60.2% ± 36.5% more cells than with PCA-ICA (five mice, five sessions per mouse, 348–1,498 cells per session) (Figure 4C). Applying our registration procedure to the detected cells, we obtained a probabilistic model of the data without the need for any adaptations to our method (Figures 4D–4F). Although we detected a higher density of cells with CNMF-E, we could, nonetheless, register cells (198,230 neighboring cell-pairs) with certainty levels, false-negative rates, and false-positive rates comparable to those obtained with PCA-ICA (Figures 4G and 4H).

Figure 4.

The Cell Registration Method Is Applicable to Different Types of Imaging Data

(A–H) Registration is applicable to cells detected using CNMF-E.

(A) Projection of all spatial footprints for three imaging sessions recorded on three different days, indicated in red, green, and blue.

(B) Overlay of the aligned spatial footprint maps shown in (A).

(C) Overlay of spatial footprint maps detected using PCA-ICA (red) and CNMF-E (green) for the same session.

(D and E) Distributions of centroid distances (D) and spatial correlations (E) between all neighboring cell-pairs (blue bars) and the modeled distributions of same cells (dashed green curves), different cells (dashed red curves), and their weighted sum (solid black curves). Gray dashed lines show the intersection between the two distributions. Estimated fractions of same cells (green) or different cells (red) above and below these intersections are indicated.

(F) Contours of P_same overlaid on the joint distribution of centroid distances and spatial correlations for neighboring cell-pairs. Numbers of cell-pairs are displayed in a logarithmic scale. The P_same = 0.05, P_same = 0.5, and P_same = 0.95 contours are highlighted by thicker white, gray, and black curves, respectively.

(G) The cumulative fraction of cell-pairs as a function of the estimated P_same for the centroid distances (red), spatial correlations (blue), and joint (green) models. Black dashed horizontal lines represent the P_same = 0.05 and P_same = 0.95 levels, while the vertical lines show the joint model’s intersection with those probabilities. Inset: the fraction of cell-pairs in the uncertain registration range (mean ± SEM).

(H) Estimated ROC curves for the centroid distances (red), spatial correlations (blue), and joint (green) models. Inset: zoom-in on the near-optimal part of the ROC. Black asterisks represent the P_same = 0.5 threshold. Data in (G) and (H) were pooled from five mice.

(I–M) Registration is applicable to two-photon imaging data.

(I) Projection of all spatial footprints for three imaging sessions recorded on three different days, indicated in red, green, and blue.

(J) Overlay of the aligned spatial footprint maps shown in (I).

(K) Distribution of centroid distances for neighboring cell-pairs (blue bars) and the modeled distribution of same cells (dashed green curve), different cells (dashed red curve), and their weighted sum (solid black curve).

(L) Cumulative fraction of cell-pairs as a function of the estimated P_same for the centroid distances model (average ± SD represented by the red curve and shaded red area). Black dashed horizontal lines represent the P_same = 0.05 and P_same = 0.95 levels, while the vertical lines show the model’s intersection with those probabilities. Inset: the fraction of cell-pairs in the uncertain registration range (mean ± SEM).

(M) Average estimated ROC curve. Inset: zoom-in on the near-optimal part of the ROC obtained for each mouse individually. Black asterisks represent the P_same = 0.5 threshold. Two-photon data in (I)–(M) were obtained from the Allen Brain Observatory, 2016, based on experiments consisting of three sessions recorded on three different days in the visual cortex of head-fixed behaving mice. Data in (L) and (M) were pooled from 10 mice.

In addition, we tested our registration method on data from two-photon imaging in head-fixed behaving mice (10 mice, three sessions per mouse, 196–375 cells per session, obtained from the Allen Brain Observatory, 2016). Image alignment of the different sessions revealed that different subsets of cells were detected in each of the imaging sessions (Figures 4I and 4J), demonstrating that there was no one-to-one mapping of cell identity across sessions, consistent with previous reports (Driscoll et al., 2017, Wagner et al., 2017). As expected from the optical sectioning and higher spatial resolution of two-photon microscopy, cell registration (19,970 neighboring cell-pairs) yielded lower registration uncertainty (Figures 4K and 4L; 5.8% ± 4.8% of the neighboring cell-pairs are in the uncertain range), false-negative rates (1.4% ± 0.8%), and false-positive rates (Figure 4M; 1.3% ± 1.3%) than those obtained with one-photon microscopy. Overall, our registration method was found to be applicable to both one-photon and two-photon imaging techniques, to various cell detection algorithms, and to imaging data from different brain regions (Figures S4 and S5).

Cell Registration Is Scalable for a Large Number of Sessions

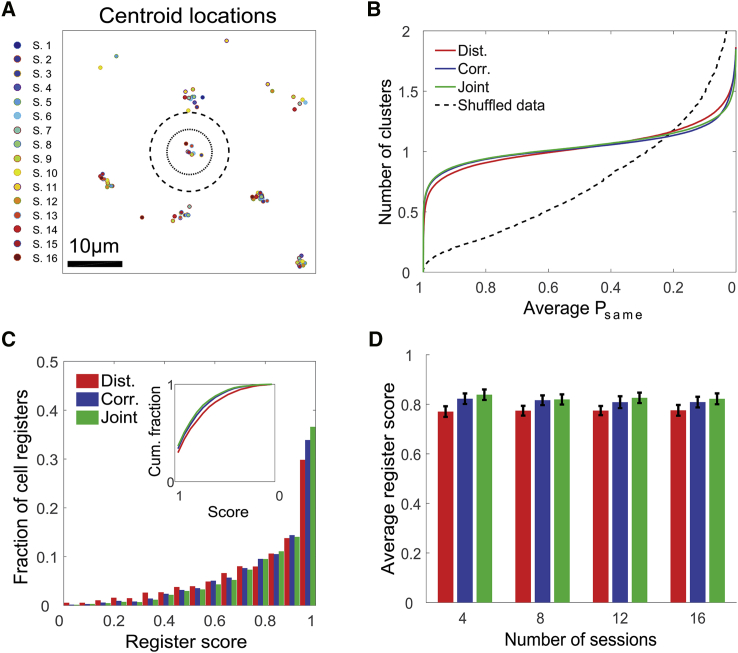
Consistent with the observed bimodal distributions of cell-pair similarity (Figure 2), the centroid locations of cells across multiple sessions seem to be spatially clustered (Figure 5A). Consequently, high P_same values are expected between cell-pairs within a cluster, whereas low P_same values are expected between cell-pairs from different clusters. Therefore, to register cells from multiple sessions as single entities, we applied a clustering procedure (Bansal et al., 2004) based on the estimated P_same. As expected, clustering of the cells from all the sessions revealed that each cell tends to have a high P_same with one and only one cluster (Figure 5B).

Figure 5.

Accurate Cell Registration Is Scalable for a Large Number of Sessions

(A) Centroid locations of cells from 16 different sessions taken from a small part of the FOV. The inner circle represents a radius of 4 μm, and the outer (dashed) circle represents a radius of 7 μm.

(B) The number of candidate clusters per cell remains ∼1 over a wide range of average P_same values for the centroid distances (red), spatial correlations (blue), and joint (green) models but not for the shuffled data (black dashed curve).

(C) Distribution of register scores for the centroid distances (red), spatial correlations (blue), and joint (green) models. Inset: cumulative fraction of cell registers as a function of the register score reversed from 1 to 0.

(D) Register score as a function of the number of registered sessions for the centroid distances (red), spatial correlations (blue), and joint (green) models (mean ± SEM).

Data in (B) and (C) were pooled from 12 mice. Data in (D) were pooled from five mice.

See also Figure S7.

The clustering procedure yields a list of entities (cell registers), each representing a single cell over multiple sessions. To quantify the registration quality for each cell register, we defined a stringent register score index (range = 0–1), which takes into account the registration certainty of all cell-pairs within the cluster (Figures 5C and S7). Register scores (10,102 cell registers pooled from 12 mice) were higher for the joint model relative to the centroid distances model (average register score of 0.78 ± 0.02, 0.81 ± 0.02, and 0.82 ± 0.02, for the centroid distances, spatial correlations, and joint models, respectively; repeated-measures ANOVA, F(1, 5) = 10.8, p = 0.024). To test whether cell registration accuracy is maintained over a large number of sessions over weeks, we used data recorded across 16 sessions spanning 15 days (Rubin et al., 2015) and repeatedly applied our registration method to various numbers of sessions. We did not find the average register score (4,242 cell registers pooled from five mice) to decrease with the number of registered sessions (repeated-measures ANOVA, F(2, 9) = 2.3, p = 0.129; Figure 5D), demonstrating that our registration method is scalable for a large number of sessions, rendering it suitable for longitudinal studies.

Validation of the Cell Registration Method

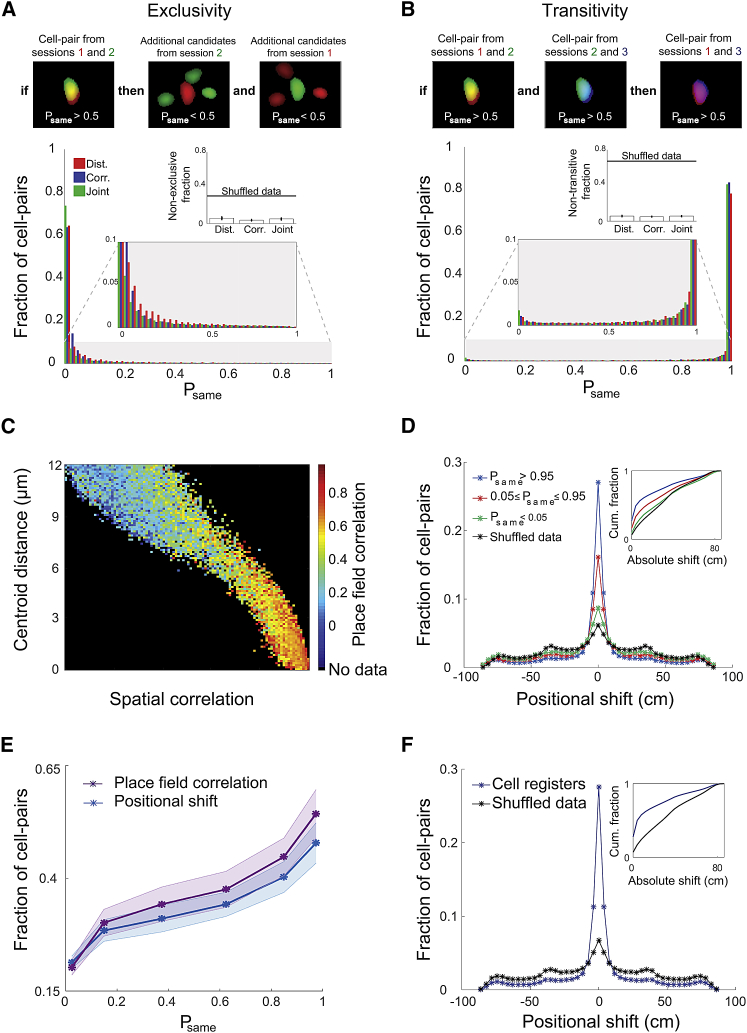
We applied several independent techniques to validate cell registration across multiple sessions, both at the cell-pair level and at the cell-register level. First, we quantified exclusivity and transitivity, two logical prerequisites for the model to be internally consistent with the data. Exclusivity requires that, if a given cell from session 1 is paired with a cell from session 2, then no other cell from session 2 be paired with it. Transitivity requires that, if a cell from session 1 and a cell from session 2 are paired, and the cell from session 2 is paired with a cell from session 3, then the cells from sessions 1 and 3 also be paired. To measure exclusivity, we focused on cells that have a pairing candidate with P_same > 0.5 in another session and calculated for these cells the distribution of P_same with all additional pairing candidates (Figure 6A). As expected, the additional pairing candidates had a low P_same with 93.9% ± 4.5%, 96.1% ± 2.4%, and 94.8% ± 3.6% of them having a P_same < 0.5 for the centroid distances, spatial correlations, and joint models, respectively, compared to 69.1% in the shuffled data (inset of Figure 6A). The joint model resulted in higher exclusivity compared to the centroid distances model (one-way repeated-measures ANOVA, F(1, 13) = 5.7, p = 0.03). To measure transitivity, we calculated the distribution of P_same for pairs of cells from two different sessions where each had a P_same > 0.5 with the same candidate from a third session (Figure 6B). Indeed, such pairs showed a high P_same with 94.1% ± 1.7%, 94.9% ± 1.2%, and 94.3% ± 1.5% of them having a P_same > 0.5 for the centroid distances, spatial correlations, and joint models, respectively, compared to 32.8% in the shuffled data (inset of Figure 6B). We found no differences in transitivity between the three different models.

Figure 6.

Validation Based on the Exclusivity and Transitivity Principles and on Place-Field Stability across Days

(A and B) Internal consistency between the model and the data. Exclusivity (A) and transitivity (B) measures for the centroid distances (red), spatial correlations (blue), and joint (green) models. (A) Top: illustration of the exclusivity principle. Bottom: distribution of P_same with additional pairing candidates, computed for cell-pairs from different sessions with P_same > 0.5. Insets: bottom, zoom-in on the lower area of the distribution; top, fraction of non-exclusive cell-pairs, i.e., P_same > 0.5 (mean ± SEM). (B) Top: illustration of the transitivity principle. Bottom: distribution of P_same for cell-pairs from different sessions, where each had P_same > 0.5 with the same cell from a third session. Insets: bottom, zoom-in on the lower area of the distribution; top, fraction of non-transitive cell-pairs, i.e., P_same < 0.5 (mean ± SEM). Data in (A) and (B) were pooled from an N of 12 mice.

(C–F) Validation based on place-field stability across days.

(C) Average place-field correlation between cell-pairs across days given their centroid distances and spatial correlations. The black area represents centroid distances and spatial correlations with no cell-pairs.

(D) Distribution of place-field positional shifts across days for cell-pairs with P_same > 0.95 (blue), 0.05 ≤ P_same ≤ 0.95 (red), and P_same < 0.05 (green) and for shuffled data (black). Inset: the cumulative fraction of cell-pairs as a function of the absolute value of the positional shift.

(E) Average fraction of neighboring cell-pairs with positional shifts ≤6 cm (blue) or place-field correlations >0.5 (purple) increase with P_same (linear regression: r² = 0.94, p = 0.0015; and r² = 0.93, p = 0.0018, respectively; SD is indicated with a shaded area).

(F) Distribution of place-field positional shifts for cell-pairs taken from cell registers (blue) and shuffled data (black). Inset: the cumulative fraction of cell-pairs as a function of the absolute value of the positional shift. Data in (C)–(F) were pooled from an N of 5 mice.

See also Movie S1.

For an independent validation of the probabilistic approach, we applied our registration method to data recorded from hippocampal CA1 cells in mice that explored linear tracks (Rubin et al., 2015), focusing our analysis on place cells. Place cells, which are abundant in the hippocampus, selectively fire when an animal moves through a particular location in space (O’Keefe and Dostrovsky, 1971). Previous work has shown that place cells that are active on different days tend to maintain their coding specificity, i.e., display stable place fields (Thompson and Best, 1990, Kentros et al., 2004, Ziv et al., 2013). Therefore, cell-pairs with a high P_same are presumed to display more similar place fields across days than expected by chance (see Movie S1 for examples of place cells). Cell-pairs (158,488 pairs of place cells pooled from five mice) with high spatial correlations and low centroid distances demonstrated high place-field correlations (Figure 6C), consistent with the notion that they are the same cell. We divided cell-pairs into three subsets: (1) high probability of being the same cell (P_same > 0.95); (2) uncertain registration range (0.05 ≤ P_same ≤ 0.95); and (3) high probability of being different cells (P_same < 0.05). We calculated for each subset the place-field positional shifts and place-field correlations across days (Figures 6D and 6E) and compared them to the distribution obtained for shuffled data. As expected, cell-pairs with a higher P_same had higher probabilities to display minor positional shifts and high place-field correlations across days (48.8%, 33.1%, and 21.4% of cell-pairs had a place-field positional shift ≤6 cm for P_same > 0.95, 0.05 ≤ P_same ≤ 0.95, and P_same < 0.05, respectively, compared to 15.9% in shuffled data). Additionally, to validate our clustering procedure, we measured the place-field stability of cell registers across multiple sessions (Figure 6F). Cell registers (3,531 place cell registers pooled from five mice across eight sessions) had considerably more stable place fields across days than shuffled data (50.0% of the pairs within cell registers had a place-field positional shift ≤6 cm, compared to 17.0% for shuffled data), consistent with previous studies (Ziv et al., 2013, Rubin et al., 2015). The comparable levels of place-field stability observed for cell registers and for cell-pairs with P_same > 0.95 imply that cells from multiple imaging sessions that were registered together, indeed, have a high probability to be the same neuronal entity.

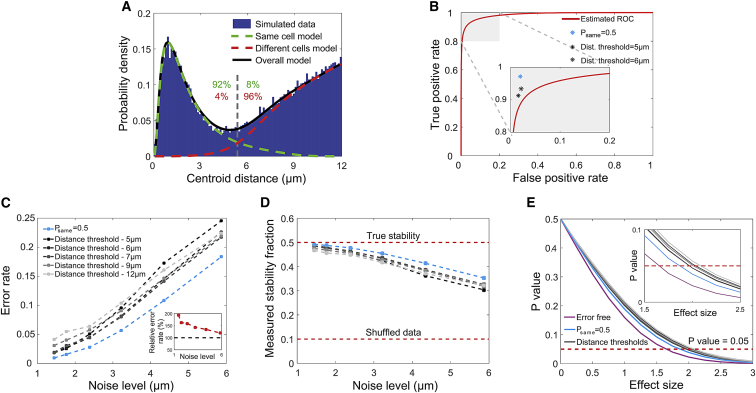
Finally, we sought to use simulated data to validate our cell registration method across multiple sessions and evaluate its performance relative to previously used routines. We simulated the centroid locations of cells across multiple sessions based on the distribution of centroid distances of same cells estimated from the data. Applying our registration procedure to the simulated data (Figure 7A), we obtained the estimated false-positive and false-negative rates (Figure 7B), as in Figure 3D. We then compared the actual false-positive and false-negative rates obtained with a registration threshold of P_same = 0.5 to those obtained with previously used centroid distance thresholds of 5 μm (Jennings et al., 2015, Cai et al., 2016) and 6 μm (Ziv et al., 2013, Rubin et al., 2015). We found that our method yielded lower false-negative rates than registration routines used in previous studies (3.7% versus 8.6% and 6.8% for 5 μm and 6 μm, respectively) while maintaining comparable false-positive rates (1.9% versus 1.8% and 2.1% for 5 μm and 6 μm, respectively). To study the performance of our method on imaging datasets of different quality levels, we simulated different noise levels and compared our registration method to registration using various centroid distance thresholds (Figure 7C). Our method yielded more accurate registrations across all noise levels and all registration thresholds. For the range of noise levels typically observed in one-photon imaging (1.5–3.5 μm; inset of Figure 7C), using the best of all tested thresholds for each noise level resulted in 43%–63% more registration errors than with our method. The decreased fraction of registration errors of our method yielded a more accurate estimation of neuronal coding stability (Figure 7D) and decreased the effect size required to expose coding stability that is significantly higher than chance levels (Figure 7E). While the effect size in this case (comparable to that observed experimentally for hippocampal place cells) is too large to be obscured by registration errors, other stability measures with smaller effect sizes may be more significantly impacted by registration accuracy. Notably, for different noise levels, different centroid distance thresholds yielded more accurate registration (Figures 7C and 7D). Since the optimal registration threshold is not known a priori, using a fixed centroid distance threshold decreases registration accuracy, further emphasizing the advantage of our method over previously used “one-size-fits-all” threshold-based registration.

Figure 7.

Validation Based on Simulated Data

(A) Distribution of centroid distances for neighboring cell-pairs (blue bars) and the modeled distribution of same cells (dashed green curve), different cells (dashed red curve), and their weighted sum (solid black curve). Estimated fractions of same cells (green) or different cells (red) above and below the intersection are indicated.

(B) Estimated ROC curve. Inset: zoom-in on the near-optimal part of the ROC. Asterisks represent the actual true-positive and false-positive rates obtained with a registration threshold of P_same = 0.5 (blue), centroid distance of 5 μm (black), and centroid distance of 6 μm (dark gray).

(C) Error rate (weighted average of false-positive and false-negative rates) as a function of the noise level, for a registration threshold of P_same = 0.5 (blue) and different centroid distance thresholds (shades of gray). Inset: the error rate obtained with the best centroid distance threshold (red dashed line) relative to the error rate obtained with a P_same value of 0.5 (black dashed line). Noise level is the mean centroid distance between the spatial footprints of the same cell in different sessions.

(D) Measured fractions of neurons with stable coding as a function of the noise level, for a registration threshold of P_same = 0.5 (blue) and different centroid distance thresholds (shades of gray), compared to the true stability level and the stability fraction for shuffled data (red lines).

(E) The significance of the difference between the measured stability and the shuffled data as a function of the true population effect size, for registration with a threshold of P_same = 0.5 (blue) and with different centroid distance thresholds (shades of gray), compared to an error-free measurement (magenta). Inset: zoom-in on the area with a P of 0.05. Effect size is the difference between the mean stability of the population and shuffled data divided by the stability SD.

For (A), (B), and (E), a noise level of 3.2 μm was used.

Discussion

We investigated the ability to reliably track the same neurons across multiple weeks in Ca²⁺ imaging data and developed a method for automated cell registration across sessions. Because not all cells can be registered with certainty as same cells or as different cells, we used a probabilistic approach that estimates the confidence of registration associated with each cell in the data. Using a Bayesian framework, we estimated the probability of neighboring cell-pairs from different sessions to be the same cell (P_same), given their spatial correlation and centroid distance. All three tested models that are based on our probabilistic approach (centroid distances, spatial correlations, and joint) yielded high confidence levels of registration for a great majority of the cells (Figures 3C, 3D, and 5C). Importantly, we did not find registration accuracy to decrease as a function of the number of registered sessions (Figure 5D), suggesting that our method is scalable for a large number of sessions and demonstrating its utility for longitudinal studies.

We found that registration based on spatial correlations and on the joint models was slightly superior to that based on centroid distances. This result is consistent with the fact that spatial correlations account for the contribution of each pixel to the cell’s fluorescence, thus carrying additional information about cell identity that is absent in the previously used centroid distance measure. Moreover, while optical aberrations (typical to gradient refractive index [GRIN] lens objectives used with miniature one-photon microscopes) may affect the measured centroid distance and result in larger distances in the periphery of the FOV, the spatial correlation is less sensitive to such artifacts.

Our method offers several measures to evaluate the suitability of the data for longitudinal studies. The measured distribution of spatial footprint similarities (either centroid distance or spatial correlation) across sessions constitutes one such measure: the greater the separation between the distributions for same cells and for different cells, the higher the accuracy of cell registration that can be obtained. Although this level of separation cannot be measured directly from the data, it is nevertheless reflected in the bimodality of the distribution for all neighboring cell-pairs across sessions (Figures 2D, 2E, and 2H). Our probabilistic approach is based on the quantification of this bimodality, providing the estimated false-positive and false-negative rates for different registration thresholds. These measures were lacking in previous works. This quantification also allows for adjusting the balance between conservativeness and permissiveness by controlling the tradeoff between false-positive and false-negative rates (Figure S7). For example, when studying the long-term stability of the coding properties of individual neurons, choosing a conservative registration threshold (e.g., P_same = 0.95) may be more appropriate (see the differences in place-field stability in Figure 6D). Additionally, the method quantifies the registration quality of each cell register in the data, which enables the inclusion, in the analysis, of only cell registers with high confidence levels. Finally, the method provides quantifications that can be used to evaluate the stability of the preparation (Figure S2) and detect abnormalities (e.g., changes in the focal plane over time). Taken together, these evaluations provide objective measures of data quality (Harris et al., 2016) that can help researchers determine whether their data are adequate for longitudinal analysis and to adaptively utilize the cell registration procedure to suit the specific needs of the study.

We validated our cell registration method using three independent analyses: (1) exclusivity and transitivity, which demonstrated internal consistency between the model and the data (Figures 6A and 6B); (2) coding stability of place cells that provided an unbiased validation of the method, since coding properties were not used for cell registration (Figures 6D–6F); and (3) registration of simulated data for which the ground truth is known, which demonstrated superior performance of our registration method over previously used routines that apply a predetermined centroid distance threshold (Figures 7B and 7C). This improved performance stems from two factors: (1) the probability model allows optimizing the registration threshold to the imaged dataset, and (2) the clustering procedure uses additional information from all neighboring cells across all sessions.

The method that we introduce here is particularly tailored for large-scale, one-photon imaging data, e.g., data collected using miniature fluorescence microscopes in freely behaving rodents. Indeed, for two-photon imaging data, there are alternative methods for cell registration that are based on image alignment between a dynamic marker (e.g., GCaMP6) and a structural reference marker (e.g., a red fluorescent protein that is expressed in the nucleus; Rose et al., 2016), which enables one-to-one mapping between sessions. Such a method, however, cannot be used with one-photon imaging data due to lack of optical sectioning and light scattering, which preclude the resolution of fine structures (e.g., cell nucleus) from non-dynamic markers in dense labeling schemes.

We demonstrated the applicability of our registration method to data recorded from GCaMP6f/s-expressing neurons in the hippocampus and prefrontal cortex of both virus-injected and transgenic mice (Figures S4 and S5). We also found our registration procedure to be robust to various imaging techniques and cell detection algorithms: PCA-ICA and CNMF-E for one-photon data (Figures 1 and 4A–4H) and normalized periodical projection for two-photon data (Figures 4I–4M). While other types of data may require some adaptations to our method (e.g., the use of other similarity measures or functional forms to model the distribution of the data), the probabilistic approach we used is general and can accommodate such adaptations. The registration procedure is fully automated and does not require manual inspection of each cell, making it scalable for very large FOVs (Kim et al., 2016, Pachitariu et al., 2016, Sofroniew et al., 2016). In this respect, it aligns with current algorithms for cell detection in large-scale Ca²⁺ imaging data. Overall, our cell registration method expands the toolset available for analysis of time-lapse imaging data, offering the potential to explore coding dynamics within the same cells and neuronal ensembles over timescales of many weeks and even months.

Experimental Procedures

Animals and Ca²⁺ Imaging Procedures

All procedures were approved by the Weizmann Institute’s Institutional Animal Care and Use Committee. For time-lapse imaging in freely behaving mice using an integrated miniature fluorescence microscope (nVistaHD, Inscopix), we followed a previously established protocol (Ziv et al., 2013). We used data from a total of 12 male mice. Mice were housed in a reverse-light-cycle facility and were 8–12 weeks old at the beginning of the study. For Ca²⁺ imaging in the hippocampal CA1, we used five Thy1-GCaMP6f mice (Jackson Laboratory, #025393) (Dana et al., 2014) and five adeno-associated virus (AAV)-injected C57BL/6 wild-type mice (data from four out of five wild-type mice were taken from our previous work; Rubin et al., 2015). For Ca²⁺ imaging in the prefrontal cortex, we used two CaMKII-tTA and rtTA-GCaMP6s double-transgenic mice (CamKII-GCaMP6s, for short) (Tg(tetO-GCaMP6s)2Niell; Jackson Laboratory, #024742; and B6.Cg-Tg(CaMK2a-tTA)1Mmay/DboJ; Jackson Laboratory, #007004). Ca²⁺ imaging of the virus-injected and transgenic mice were performed at 20 Hz and 10 Hz, respectively. Additionally, we obtained published two-photon imaging data from ten different experiments from the Allen Brain Observatory, 2016 (http://observatory.brain-map.org/visualcoding). For a detailed description of the surgical and Ca²⁺ imaging procedures, see the Supplemental Experimental Procedures.

Processing of Ca²⁺ Imaging Data

We processed imaging data using commercial software (Mosaic, v1.1.1b, Inscopix) and custom MATLAB routines, as previously described (Rubin et al., 2015). Briefly, the procedure consisted of the following main stages: (1) spatial down-sampling (final pixel size of 2.3 μm × 2.3 μm) to increase computational speed; (2) image registration to correct for lateral displacements of the brain; (3) transformation into relative changes in fluorescence, $\Delta F\left(t\right)/F_0=\left(F\left(t\right)-F_0\right)/F_0$, where F₀ is the value for each pixel averaged over time; (4) detection of cells and extraction of their spatial footprints using PCA-ICA (Mukamel et al., 2009); (5) extraction of each cell’s fluorescence trace by applying the spatial footprints to the $\Delta F\left(t\right)/F_0$ movies; and (6) detection of Ca²⁺ events using thresholding of the fluorescence trace. As an independent technique for cell detection, we also used CNMF-E (Zhou et al., 2016), an extension of the CNMF method (Pnevmatikakis et al., 2016), for one-photon microendoscopic data. For a detailed description of the processing routines, see the Supplemental Experimental Procedures.

Registration of Cells across Sessions

We developed a probabilistic method for registering cells across multiple sessions based on the similarity in their spatial footprints. We used two similarity measures, the distance between centers of mass of two spatial footprints (centroid distance) and the Pearson correlation between spatial footprints (spatial correlation), to decide whether pairs of neighboring cells from two different sessions are the same entity. We registered cells using three main stages: (1) image alignment; (2) probabilistic modeling of the data; and (3) cell registration with a clustering procedure.

(1) Image Alignment

For each session, we projected the centroid locations of all the cells’ spatial footprints onto a single image. We computed the cross-correlations between the projections of each session with the projection of a reference session, examining different rotations. We corrected for translation and rotation differences between the sessions by applying the translations and rotations that resulted in the maximal cross-correlation, yielding each cell’s location in the reference coordinate system.

(2) Probabilistic Modeling of the Data

We modeled the distributions of centroid distances (centroid distances model) and spatial correlations (spatial correlations model) as a weighted sum of the distributions of two subpopulations of cell-pairs, representing same cells and different cells. Specifically, we modeled the distribution of centroid distances for different cells as a multiplication of a sigmoid function by a linear function. To model the distribution of centroid distances for the same cells, we used a log-normal distribution to match the requirement of a non-negative distribution. Similarly, the distribution of spatial correlations for same cells was modeled as a log-normal distribution. Since the distribution of spatial correlations peaks close to 1, we defined the origin as 1 by taking 1 minus the spatial correlation value. We modeled the distribution of spatial correlations for different cells using a beta function to obtain a single peaked distribution between 0 and 1. For each model, we found the parameters of the distributions and weights that best fit the data in terms of the mean squared error (performed for each mouse individually). Applying similar principles, we modeled the joint distribution of centroid distances and spatial correlations (joint model) for neighboring cell-pairs. For a detailed description of the probabilistic models, see the Supplemental Experimental Procedures and Figure S6. To obtain the probability for any pair of neighboring cells from different sessions to be the same cell, given their spatial correlation and centroid distance, we calculated P_same(dist,corr), according to Bayes’s rule:

$$P_{same}\left(dist,corr\right)=\frac{P\left(dist,corr|same\right)\cdot W_{same}}{P\left(dist,corr|same\right)\cdot W_{same}+P\left(dist,corr|diff\right)\cdot W_{diff}}$$

where W_same and W_diff are the estimated weights (prior probabilities) for the two subpopulations of same cells and different cells, respectively. P(dist,corr|same) and P(dist,corr|diff) are the estimated joint distributions of centroid distances and spatial correlations for same cells and different cells, respectively. Similar calculations were performed for each of the one-dimensional models.

(3) Cell Registration with a Clustering Procedure

We applied an iterative clustering procedure (Bansal et al., 2004) based on the estimated P_same. First, we created an initial list of cells based on a P_same threshold. The iterative clustering procedure was then applied, and each cell was clustered with the candidate from all the different sessions with which it had the highest P_same. If P_same was lower than the registration threshold, the cell formed a new cluster. The iterative process continued until the clustering procedure converged.

Quantification of Registration Accuracy

Cell-Pairs

For the centroid distances model, the false-negative rate was estimated as the fraction of the model of same cells that is higher than the registration threshold:

$$Falsenegativerate=\frac{\#falsenegatives}{\#falsenegatives+\#truepositives}.$$

The false-positive rate was estimated as the fraction of the model of different cells that is lower than the registration threshold:

$$Falsepositiverate=\frac{\#falsepositives}{\#falsepositives+\#truenegatives}.$$

Additionally, we calculated the Gini coefficient G₁ and the overall estimated registration accuracy (see the Supplemental Experimental Procedures). Similar calculations were performed for the spatial correlations and joint models.

Cell Registers

The register score was calculated for each registered cell as the total number of reliable cell-pairs out of the total number of pairwise combinations of cell-pairs from all sessions. Each pair was considered reliable if it met three criteria (see the Supplemental Experimental Procedures). Accordingly, we defined the register score as:

$$\mathit{register}\mathit{score=}\frac{\mathit{1}}{\tilde{\mathit{N}}\left(\mathit{N-1}\right)}\sum _{\mathit{k=1}}^{\tilde{\mathit{N}}}\sum _{\begin{array}{c}\mathit{m=1}\\ \mathit{m\ne k}\end{array}}^{\mathit{N}}\mathit{\delta }\left(\mathit{k,m}\right)$$

where N is the total number of sessions, $\tilde{\text{N}}$ is the number of active sessions for a given cell register, and $\mathrm{\delta }\left(\mathrm{k,m}\right)$ is 1 if a cell-pair in the cluster is reliable and 0 otherwise. To examine the scalability of the method for a large number of sessions, registration was performed simultaneously for multiple sessions with the clustering procedure, choosing random subsets of the 16 sessions comprising 4, 8, or 12 sessions, and for the entire set of 16 sessions.

Validation of Cell Registration

Exclusivity and Transitivity Measures

To compare exclusivity and transitivity of the data with those expected by chance, we obtained shuffled data by measuring the centroid distances between cell-pairs from different sessions, where each session was taken from a different mouse (see the Supplemental Experimental Procedures).

Place-Field Stability

We analyzed mouse behavior videos using a custom MATLAB (Mathworks) routine and considered periods wherein the mouse ran >3 cm/s. We divided each linear track into 24 bins (4 cm each) and computed the activity map (event rate per bin) for each neuron by dividing the smoothed (Gaussian kernel: σ = 1.5 bins, size = 5 bins) map of Ca²⁺ event numbers by the smoothed map of occupancy (Rubin et al., 2015). We defined the place field as the peak value of the activity map. For each place field with ≥5 events for a given session, we computed the spatial information using the unsmoothed event-rate map of each cell, as previously described (Markus et al., 1994) (see the Supplemental Experimental Procedures). Cells with statistically significant spatial information were considered as place cells. We then calculated the place-field positional shift and place-field correlation (Pearson correlation) for cell-pairs from different sessions for which at least one cell in the pair was considered a place cell. To compare the place-field stability of the data with the stability expected by chance, we obtained shuffled data by randomizing the identity of cells across sessions.

Simulated Data

Simulated data were obtained by using representative spatial footprints of cells that were detected in our data and placing them in a random location in the FOV. The minimal centroid distance between the locations of neighboring cells was set to 7 μm ± 1 μm (normally distributed) to match the distribution of the observed data. In each session, a fraction of the cells was simulated as active, and their locations were set as the original centroid locations with a jitter (see the Supplemental Experimental Procedures). The fraction of active cells and the radius of the jitter were chosen to match those of the observed data. To obtain simulated data with different noise levels, we systematically increased the radius of the centroid location jitter. Additionally, we simulated the effects of registration errors on measurements of the stability of the functional properties of cells. To test whether registration errors could obscure conclusions drawn from the data, we systematically changed effect sizes by changing the percentages of same cells that maintain their coding properties across sessions. Effect size was defined as the difference between the mean stability of the population and shuffled data, divided by the stability SD.

Statistical Analysis

For related sample analysis, we performed repeated-measures ANOVA. Greenhouse-Geisser estimates of sphericity were used for adjustment of degrees of freedom, and Bonferroni correction was performed when conducting multiple comparisons.

Code and Data Availability

The cell registration software, including a sample dataset that enables the generation of most of the figures presented in this paper, is deposited in a GitHub repository that can be accessed freely: https://github.com/zivlab/CellReg.

Author Contributions

L.S. developed the cell registration method, designed and performed analyses, and wrote and edited the paper. A.R. developed the cell registration method, designed analyses, and edited the paper. N.B.-E. performed experiments and analyses. N.G. performed experiments. N.S. performed experiments. O.P. performed analyses. Y.Z. supervised the project, designed analyses, and wrote and edited the paper.

Published: October 24, 2017

Supplemental Information

Movie S1. The Same Place Cells Show Similar Place Fields in Different Days of Imaging, Related to Figure 6

From top to bottom: DF/F₀ of Ca²⁺ dynamics for 120 seconds (shown in X2 of true speed), taken from two different recording sessions separated by two days. The contours of the spatial footprints of six example place cells are overlaid on the DF/F₀ movie. The mouse behavior and DF/F₀ traces for the example cells are shown. The location of the mouse within the linear track for each detected Ca²⁺ event is plotted separately for each of the example place cells. Data recorded in the hippocampal CA1 of a Thy1-GCaMP6f transgenic mouse while freely exploring the same linear track.