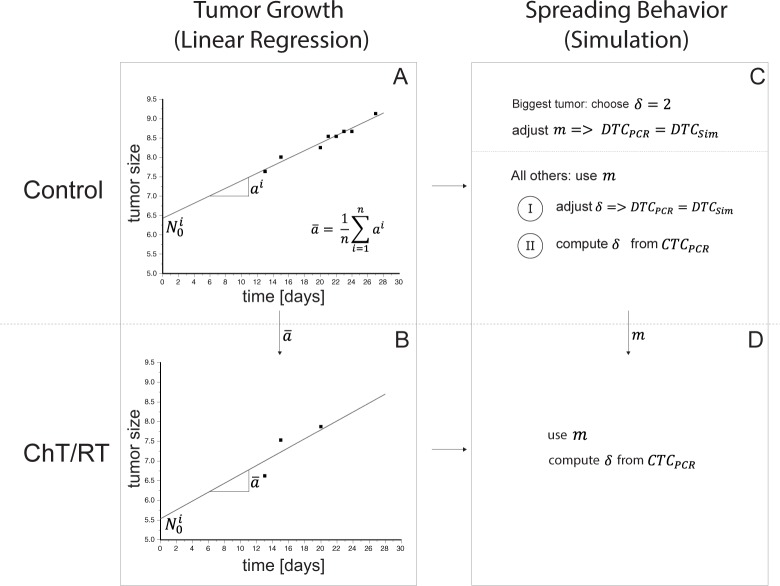
Fig 1. Overview of the workflow used to analyze the experimental data.

Panel A shows the linear regression procedure to determine the number of engrafted tumor cells $N_0^i$ and the growth rate constant aⁱ for each mouse i from the untreated tumor bearing mice of the control group. In Panel B, the mean growth rate constant $\overline{a}$ from the animals of this control group was used to determine the number of engrafted tumor cells in the groups of animals that were treated with radiotherapy or chemotherapy by using only the data points which were unaffected by therapy because we need a parametrization of the normal growth behavior of the tumor since the therapy effect will be modelled separately. Using this approach, the effects of the therapy do not affect the parametrization of the growth function. Panel C shows the approach to determine the spreading behavior in the control group, which is represented by the colonization coefficient m and the fractal dimension δ. Parameters were determined in two different ways: (I) from the experimentally determined numbers of disseminated tumor cells (DTC) and (II) from the experimentally numbers of circulating tumor cells (CTC). For the mouse with the biggest tumor we choose a fractal dimension of 2, which implies a blood supply on the surface of the tumor, to determine the colonization coefficient. Afterwards, we calculated with these data all other parameters for the remaining mice in the control group. In Panel D, the determined parameter m will be used to compute the fractal dimension δ in treated groups with its own growth parameters which were determined in panel B.