Figure 7. Adaptive binning recovers the power law in the face of consistent rate changes when dynamics remain critical.

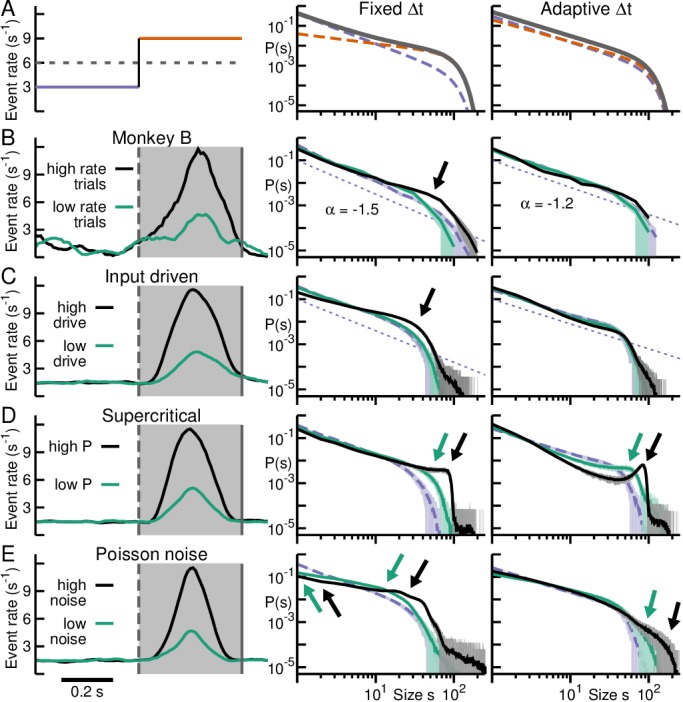
(A) Schematic impact of avalanche analysis from non-stationary event rates. Left: A low event rate period (purple) followed by a high event rate period (orange) results in an intermediate Δt (fixed binning) based on the mean event rate (broken line). Middle: The superposition of two power laws with different slopes from their corresponding rate regime (broken lines) results in an avalanche size distribution (grey) that deviates from a power law, with a characteristic up-ward bend at the cross-over point. Right: Adaptive binning steepens/reduces the slope for the high/low rate period respectively resulting in a distribution collapse at an intermediate slope. (B) Left: Average nLFP rate for monkey B with trials separated into high (black) and low (green) nLFP rate during PRE (shaded area). Middle: Corresponding distributions obtained with fixed binning increasingly deviate with rate (arrow) from baseline (broken, purple). Right: Adaptive binning collapses all distributions. (C) Simulations using a transient external Poisson drive match experimental findings (cp. B). (D) In simulations with transiently switching from critical to supercritical dynamics (left), adaptive binning fails to compensate for overabundance of large avalanche sizes from supercritical dynamics (middle/right). (E) Simulations using transient Poisson noise. Distributions obtained with fixed binning do not follow power laws, even in the low-noise regime (middle). Distributions obtained with adaptive binning do not have a clear cut-off (right).