Fig. 4. Spin-orbit–coupled honeycomb lattices and Weyl nodes.

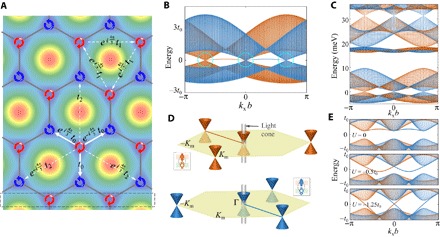
(A) Opposite photon emission polarization at A and B sites and complex hopping matrix elements for the spin-up exciton. (B) Exciton spectrum at V(A) = V(B) and moiré period b = 10 nm, from the tight-binding model with the third NN hopping. t₀ = 2.11 meV, t₁ = 0.25 meV, and t₂ = 0.14 meV. The bands feature a Dirac node and two Weyl nodes (highlighted by dotted circles). These magnetic monopoles are linked by an edge mode at a zigzag boundary, with spin polarization reversal at the Dirac node. Spin-down (spin-up) exciton is denoted by brown (blue) color. (C) Exact exciton spectrum in this superlattice potential (see section S4). Dirac/Weyl nodes are also seen in higher energy bands. (D) Schematic of the Dirac cones for the spin-up and spin-down excitons in the moiré–Brillouin zone (m-BZ), and edge modes at a zigzag boundary. Exciton-photon interconversion can directly happen within the shown light cone. (E) The Dirac and Weyl nodes are gapped by a finite A-B site energy difference Δ = 0.5t₀, whereas the edge band dispersion is tuned by changing the on-site energy of the dots on the zigzag boundary [enclosed by the dashed box in (A)] by the amount U.