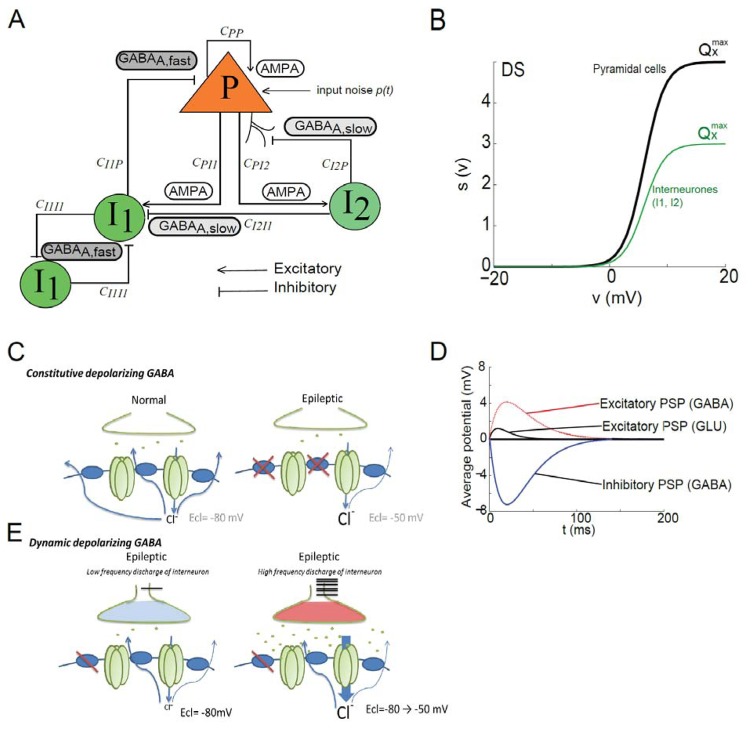
Fig 1. Computational Neural mass model of epileptic activity.

(A) Structure of the neuronal population model accounting for three sub-populations of neurons: (i) pyramidal cells (P), (ii) soma- and proximal-dendrite-targeting cells (type I1 mediating GABA_A, fast currents), and (iii) dendrite-targeting cells (type I2 mediating GABA_A, slow). Pyramidal cells receive excitatory input from other pyramidal cells (collateral excitation) or inhibitory input from interneurons. These latter cells receive excitatory input only from pyramidal cells. Besides synaptic transmission, interactions between neuronal subpopulations are also characterized in the model by connectivity constants (CPP, CPI₁, CI₁P, CI₁I₁, CPI₂, CI₂P) which account for the average number of active synaptic contacts or “connection strength” between considered sub-populations. In addition, the nonspecific influence from neighboring or distant populations is represented by a Gaussian input noise p(t) corresponding to an excitatory input that globally describes the average density of afferent action potentials (Adapted from Molaee-Ardekani et al, 2010).

(B) The classical wave-to-pulse function was modified to account for the SCN1A mutation found in the Dravet syndrome. According to the neural mass modeling approach, the wave-to-pulse function relates the average pulse density of action potentials fired by the neurons S_x(ϑ) to the average postsynaptic potential ϑ (in mV) and accounts for the saturation and threshold effects taking place at the soma. For a given sub-population X, it is modeled by a static nonlinear function of sigmoidal shape $S_{\mathrm{x}}(\vartheta )=Q_{\mathrm{x}}^{max}/(1+e^{{\mathrm{r}}_{\mathrm{x}}({\vartheta }_{\mathrm{x}}-\vartheta )})$ where $Q_{\mathrm{x}}^{max}$ is the maximum firing rate, r_x is the steepness of the sigmoid and ϑ_x is the postsynaptic potential corresponding to a firing rate of $Q_{\mathrm{x}}^{max}/2$ . In the proposed DS model (green line), $Q_{\mathrm{x}}^{max}$ parameter for both inhibitory sub-populations (I1 and I2) was reduced by 40% as compared with the pyramidal cell sub-population (black solid line). This reduction accounts for a strong decrease of the maximal interneuronal firing rate found in DS.

(C) Static depolarizing GABA. Left: In normal tissue, the high expression of chloride transporters in the GABAergic post-synaptic compartment, allows efficient extrusion of chloride outside the targeted neuron, responsible for hyperpolarized reversal potential (E_Cl=−80mV) of GABA_A IPSP. Right: In epileptic tissue, the expression of chloride transporter at the membrane is decreased at least in some neurons, leading to a “static” more positive reversal potential (E_Cl=−60mV) of GABA_A IPSP.

(D) Time course of the average excitatory and inhibitory postsynaptic potentials (PSPs) in the DS model. Depolarizing GABA was implemented in the model as an excitatory signal obeying the kinetics of GABA_A-mediated PSP (red line).These kinetics are defined by the time constant used the pulse-to-wave function (either excitatory or inhibitory) that determines both the rise time (t_rise) and the decay time (t_decay) of the PSP. As t_rise and t_decay depend mainly on intrinsic ionotropic channel properties and as the direction of the current depends mainly on the reversal potential of chloride, we modified the direction of the depolarizing GABA_A related PSP but not its kinetics.

(E) Dynamic depolarizing GABA. Left: In the epileptic tissue a slightly decreased expression of the chloride transporter, could lead to normal IPSP (E_Cl =−80mV) when the interneuronal activity is low. Right: When interneurons fire with a high frequency rate, it leads to massive GABA release and chloride overload into the targeted cell, and progressively and dynamically shifts E_Cl toward depolarized potential. Therefore if interneurons firing rate dramatically increases it induces a dynamic shift of GABA_A-mediated post synaptic potentials from inhibitory to excitatory effect.