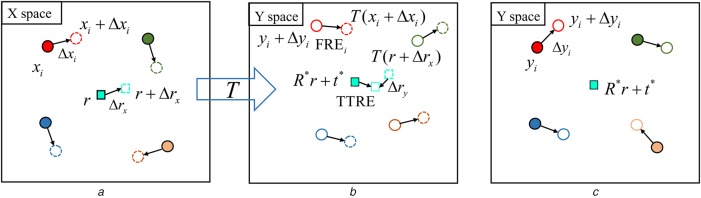
Fig. 1.

Illustrations of TTRE in a rigid registration

a X space: before registration, solid circles $\{{\mathit{x}}_i{\}}_{i=1}^N$ and open dashed circles $\{{\mathit{x}}_i+\mathrm{\Delta }{\mathit{x}}_i{\}}_{i=1}^N$ are ‘true’ and localised/measured fiducial sets, respectively. Solid square r and open dashed square $\mathit{r}+\mathrm{\Delta }{\mathit{r}}_x$ represent ‘true’ and localised target, respectively. $\{\mathrm{\Delta }{\mathit{x}}_i{\}}_{i=1}^N$ are FLE vectors and $\mathrm{\Delta }{\mathit{r}}_x$ is the TLE vector in X space

b Y space: before registration, solid circles $\{{\mathit{y}}_i{\}}_{i=1}^N$ and open circles $\{{\mathit{y}}_i+\mathrm{\Delta }{\mathit{y}}_i{\}}_{i=1}^N$ are ‘true’ and localised fiducial sets, respectively. $\{\mathrm{\Delta }{\mathit{y}}_i{\}}_{i=1}^N$ are FLE vectors in Y space

c Y space: after registration, open dashed circles $\{\mathit{T}({\mathit{x}}_i+\mathrm{\Delta }{\mathit{x}}_i){\}}_{i=1}^N$ is set of the transformed localised fiducials from X space where T is the estimated/calculated rigid transformation matrix, $\mathbf{F}\mathbf{R}{\mathbf{E}}_i$ is the FRE vector between corresponding ith fiducials after registration, open dashed square $\mathit{T}(\mathit{r}+\mathrm{\Delta }{\mathit{r}}_x)$ is the transformed localised target from X space, $\mathrm{\Delta }{\mathit{r}}_y$ is TLE vector in Y space, solid square ${\mathit{R}}^{\ast }\mathit{r}+{\mathit{t}}^{\ast }$ is ‘true’ target in Y space, $\mathbf{T}\mathbf{T}\mathbf{R}\mathbf{E}$ is the distance between ‘true’ and ‘localised’ target denoted by open square