ABSTRACT
Immunosenescence, an age-related decline in immune function, is a major contributor to morbidity and mortality in the elderly. Older hosts exhibit a delayed onset of immunity and prolonged inflammation after an infection, leading to excess damage and a greater likelihood of death. Our study applies a rule-based model to infer which components of the immune response are most changed in an aged host. Two groups of BALB/c mice (aged 12 to 16 weeks and 72 to 76 weeks) were infected with 2 inocula: a survivable dose of 50 PFU and a lethal dose of 500 PFU. Data were measured at 10 points over 19 days in the sublethal case and at 6 points over 7 days in the lethal case, after which all mice had died. Data varied primarily in the onset of immunity, particularly the inflammatory response, which led to a 2-day delay in the clearance of the virus from older hosts in the sublethal cohort. We developed a Boolean model to describe the interactions between the virus and 21 immune components, including cells, chemokines, and cytokines, of innate and adaptive immunity. The model identifies distinct sets of rules for each age group by using Boolean operators to describe the complex series of interactions that activate and deactivate immune components. Our model accurately simulates the immune responses of mice of both ages and with both inocula included in the data (95% accurate for younger mice and 94% accurate for older mice) and shows distinct rule choices for the innate immunity arm of the model between younger and aging mice in response to influenza A virus infection.
IMPORTANCE Influenza virus infection causes high morbidity and mortality rates every year, especially in the elderly. The elderly tend to have a delayed onset of many immune responses as well as prolonged inflammatory responses, leading to an overall weakened response to infection. Many of the details of immune mechanisms that change with age are currently not well understood. We present a rule-based model of the intrahost immune response to influenza virus infection. The model is fit to experimental data for young and old mice infected with influenza virus. We generated distinct sets of rules for each age group to capture the temporal differences seen in the immune responses of these mice. These rules describe a network of interactions leading to either clearance of the virus or death of the host, depending on the initial dosage of the virus. Our models clearly demonstrate differences in these two age groups, particularly in the innate immune responses.
KEYWORDS: host-pathogen interactions, immunosenescence, influenza, mathematical modeling, viral clearance
INTRODUCTION
Influenza A virus leads to about 36,000 deaths every year in the United States (1). Older members of the population are highly susceptible to influenza virus infection, accounting for about 90% of all influenza deaths (2). The increased susceptibility of the elderly to infections leads to enormous medical costs; the elderly account for about one-half of hospital stays and one-third of the prescription drug use in the United States (3). These costs will likely continue to increase well into this century, as the older population is predicted to triple by 2050, reaching about 2 billion individuals worldwide (3).
The elderly are known to exhibit increased morbidity and mortality in response to influenza virus infection due to a weakening of the immune response with age, called immunosenescence (4). Immunosenescence is a complicated remodeling of the immune response, leading to an overall weakened response to pathogens, particularly those that have not been encountered by the host previously. Both innate and adaptive responses are impacted by immunosenescence (5). Both mice and humans have been shown to exhibit dysregulated inflammation in response to infection due to immunosenescence (6). The elderly generally experience a delayed onset of innate immunity and a prolonged inflammatory response, causing excess inflammatory damage to the body and thus more persistent symptoms. Older hosts tend to have higher baseline levels of proinflammatory cytokines, a condition recently termed “inflamm-aging” (7). Elevated cytokine levels are correlated with increased inflammatory damage. In fact, elevated interleukin-6 (IL-6) levels postinfection are an accurate predictor of morbidity and mortality (5). Phagocytosis by immune cells, particularly neutrophils, also tends to decrease with age in human hosts but not in mice (8). The specific changes in the neutrophil secretion of various cytokines and chemokines in either human or murine hosts are still largely unknown. Changes in macrophage phagocytic function are also unclear, as some reports have shown no changes in macrophage phagocytosis (9), while others have shown evidence of a decline (10, 11). Decreased chemotactic responses in macrophages have also been shown (2).
The function of both T cells and B cells has been shown to decline with age, leading to an overall decline in the efficacy of flu vaccines (2). In both humans and mice, age-related thymic involution has been shown to cause a decrease in the number of naive T lymphocytes (4, 12), limiting the ability of the host to mount a defense against novel pathogens. Helper T cell function declines with age, as does the overall number of B cells in the host (13). The numbers of IgG and IgA antibodies have been shown to increase with age, although the efficacy of antibodies against specific pathogens decreases (14).
To investigate further the changing immune mechanisms that arise in immunosenescence in response to influenza A virus, we have constructed a network model of the intrahost immune response to viral infection to elucidate the differences in the immune responses of older and younger hosts. Variables included in the model represent cell types, cytokines, chemokines, interferons, antibodies, and viral load. The model features components from innate, adaptive, and humoral immunity. Cell types include macrophages, neutrophils, natural killer (NK) cells, conventional dendritic cells, plasmacytoid dendritic cells (pDCs), T cells, B cells, and epithelial cells. To activate and recruit these cells, we include cytokines and chemokines such as IL-1α, IL-1β, IL-6, IL-10, IL-12, type I and type II interferons, tumor necrosis factor alpha (TNF-α), RANTES, macrophage inflammatory protein 1β (MIP-1β), and keratinocyte chemoattractant (KC). The model also incorporates antibodies to clear the virus from the host. Interactions among the virus, cells, cytokines, chemokines, and interferon comprise the early phases of the immune response, until antibodies are eventually upregulated and clear the virus. Our Boolean model investigates the structure of these interactions and compares interactions between young and old hosts.
Boolean network models were previously shown to generate important conclusions regarding the host immune response to other infections (15–18), and we now present such a model of influenza virus infection. Initiated by the presence of a viral load in the lungs, the network propagates several processes activated to fight the infection. We match the trajectories of each component of the immune system to rich time series data from a murine model of influenza virus infection (19). Studying the time evolution of the immune response allows an analysis of the initiation and duration of these immune components and the age-related differences between hosts.
RESULTS
Boolean networks. (i) Optimized model for younger mice.
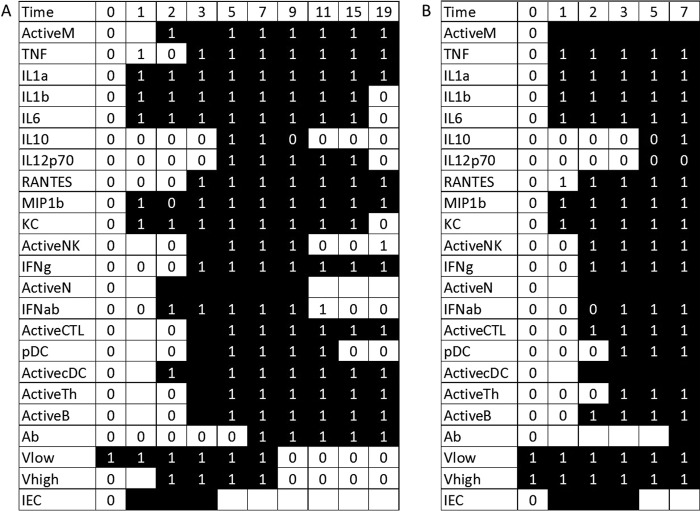
The rules modeling the younger-mouse population predict the experimental data with 97% accuracy, missing only 6 out of 197 data points in the sublethal simulations (Fig. 1A) and 4 out of 113 data points in the lethal simulations (Fig. 1B). There are 8 combinations of rules that yield this level of accuracy, and these rules are summarized in Table 1.
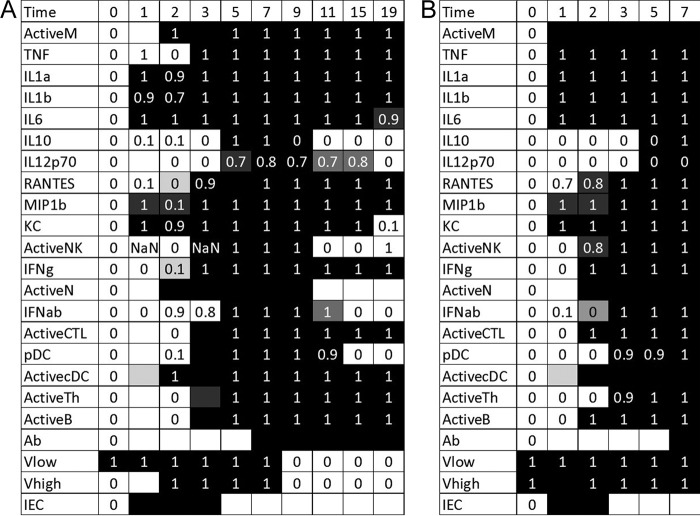
FIG 1.
Optimal fits to the full data set for younger mice in sublethal (A) and lethal (B) simulations. Experimental data are indicated with 0's and 1's. Variables for which no data were measured are indicated with a blank cell. The simulated trajectories are indicated with the shading of the table cell, where a black cell represents a variable predicted to have a value of 1 at that time point and a white cell represents a variable predicted to have a value of 0. Thus, if a black cell overlaps a value of 1, the simulation correctly predicts that variable's trajectory at that point. A white cell overlapping a value of 0 is also a correct prediction. Blank cells can predict a value of either 0 or 1 without penalty. A total of 10 data points are missed in the optimal fit.
TABLE 1.
Optimal-fit rule choices for younger and older mice
| Rule | % of models using rule |
|
|---|---|---|
| Younger mice | Older mice | |
| ActiveM ← (KC and Vlow) | TNF | 0.0 | 100.0 |
| ActiveM ← Vhigh | IL1a | 100.0 | 0.0 |
| TNF ← ActiveM | Vhigh | 50.0 | 0.0 |
| TNF ← ActivecDC | Vhigh | 50.0 | 0.0 |
| TNF ← ActiveM | 0.0 | 100.0 |
| IL1a ← ActiveM | Vlow | 50.0 | 0.0 |
| IL1a ← ActiveM | 0.0 | 100.0 |
| IL1a ← ActivecDC | Vlow | 50.0 | 0.0 |
| IL1b ← ActiveM | Vlow | 0.0 | 25.0 |
| IL1b ← ActiveM | 0.0 | 25.0 |
| IL1b ← ActivecDC | Vlow | 0.0 | 25.0 |
| IL1b ← pDC | Vlow | 100.0 | 25.0 |
| IL-6 ← ActiveM | Vlow | 0.0 | 0.0 |
| IL-6 ← ActiveM | 0.0 | 0.0 |
| IL-6 ← ActiveTh | 0.0 | 100.0 |
| IL-6 ← ActivecDC | Vlow | 0.0 | 0.0 |
| IL-6 ← pDC | Vlow | 100.0 | 0.0 |
| IL-10 ← ActiveTh & Vhigh | 100.0 | 0.0 |
| IL-10 ← ActiveNK & Vhigh | 0.0 | 0.0 |
| IL-10 ← ActiveB & Vhigh | 0.0 | 100.0 |
| IL12p70 ← ActiveTh & Vhigh | 0.0 | 0.0 |
| IL12p70 ← ActiveTh | 0.0 | 62.5 |
| IL12p70 ← ActiveM & IL1b | 0.0 | 37.5 |
| IL12p70 ← pDC | 100.0 | 0.0 |
| RANTES ← ActiveM | 100.0 | 50.0 |
| RANTES ← ActivecDC | 0.0 | 0.0 |
| RANTES ← ActiveCTL | 0.0 | 50.0 |
| MIP1b ← ActiveM | Vlow | 50.0 | 0.0 |
| MIP1b← ActiveM | 0.0 | 100.0 |
| MIP1b ← ActivecDC | Vlow | 50.0 | 0.0 |
| KC ← ActiveM | Vlow | 0.0 | 50.0 |
| KC ← Vlow | pDC | 100.0 | 50.0 |
| ActiveNK ← ActiveM | 0.0 | 100.0 |
| ActiveNK ← ActivecDC & Vlow | 100.0 | 0.0 |
| IFNg ← ActiveM | 100.0 | 100.0 |
| ActiveN ← Vlow | TNF | 0.0 | 100.0 |
| ActiveN ← KC & Vlow | 100.0 | 0.0 |
| IFNab ← (ActiveTh & Vhigh) | IEC | 100.0 | 100.0 |
| ActiveCTL ← ActiveM | 100.0 | 0.0 |
| ActiveCTL ← ActiveTh | 0.0 | 100.0 |
| pDC ← ActivecDC | 0.0 | 100.0 |
| pDC ← ActiveN | 100.0 | 0.0 |
| ActivecDC ← ActiveNK | 0.0 | 87.5 |
| ActivecDC ← IL1b | 100.0 | 12.5 |
| ActiveTh ← Vlow | ActiveM | 0.0 | 100.0 |
| ActiveTh ← ActivecDC | IL12p70 | 100.0 | 0.0 |
| ActiveB ← ActiveM | 100.0 | 100.0 |
| Ab ← (ActiveB & pDC) | Ab | 0.0 | 33.3 |
| Ab ← (ActiveB & IL-10)| Ab | 100.0 | 66.7 |
| Vlow ← (IEC | Vlow | Vhigh) & ∼(Ab) | 100.0 | 100.0 |
| Vhigh ← (IEC | Vhigh) & ∼(Ab) | 100.0 | 100.0 |
| IEC ← (Vlow | Vhigh) & ∼ActiveCTL & ∼ActiveNK | 100.0 | 100.0 |
In the sublethal case (Fig. 1A), several immune components are activated or upregulated immediately after infection is initiated, including IL-1α, IL-1β, IL-6, MIP-1β, KC, and infected epithelial cells (IECs). The quick responses of these components imply a direct impact of the viral load on their production. In this model, the direct dependence of cytokines on the virus represents upregulation by lung epithelial cells (20); since we do not have data for these cells, we represent this mechanism with a simple interaction between the virus and the cytokine. The infected cell population also increases as a result of healthy epithelial cells coming into contact with the virus. Again, this is modeled by a direct dependence on the virus itself. None of the cells in the model have measurements on day 1, so we cannot say with certainty whether or not these cells responded quickly to the presence of the virus. Our simulations do not predict a significant change from the baseline over the course of 1 day, however.
On day 2, more of the innate immune components become activated. Macrophages, neutrophils, and dendritic cells are all brought to the site of infection by the cytokines and chemokines that were upregulated on day 1. The presence of infected cells on day 1 causes an increase in type I interferon as well as an increase in the virus from low levels to high levels on day 2. There is also a decrease in the levels of MIP-1β, implying that its levels drop back to the baseline value after increasing on day 1. This is likely an anomaly in the data rather than a significant biological event. Our simulations predict that the zero on day 2 is probably incorrect.
On day 3, the cells of the model were again not measured. However, our model predicts increases in the numbers of activated NK cells, cytotoxic T lymphocytes (CTLs), pDCs, T helper cells, and B cells on day 3 in response to the high viral titers present on day 2. The data show that RANTES and TNF are upregulated on day 3 as well. TNF data also show an increase on day 1, followed by a decrease back to baseline values on day 2. Our simulations predict that the data point on day 1 is likely to be inaccurate.
The time step next jumps to day 5, when IL-10 and IL-12 are significantly produced by T helper cells or pDCs. On day 7, antibodies are produced, which then causes the virus levels to drop on day 9. When the virus clears the system, other elements of the immune system can begin to return to baseline values as well. On day 11, IL-10, NK cells, neutrophils, and type I interferon fall to baseline levels in our simulations. The data suggest that IL-10 and type I interferon levels decrease on day 9 and 15, respectively, so our simulations predict two data points incorrectly here. On day 15, pDC levels return to baseline, and on day 19, IL-1β, IL-6, IL-12, and KC levels all then decrease to baseline values as well. By the end of the simulation, 12 of the 23 variables modeled in the system returned to baseline values, signifying that the immune response was winding down and the host was healing from a survivable infection.
The simulations with a lethal inoculum (Fig. 1B) begin with a high level of virus. As a reaction to the greater presence of the virus, more innate immune components will be upregulated immediately following infection. Macrophages, TNF, IL-1α, IL-1β, IL-6, MIP-1β, and KC are each turned on in the simulation and the data, and while RANTES data predict that this chemokine should predict a value of 1 on day 1, our model misses this time point. On day 2, more of the cells are brought in, including NK cells, neutrophils, CTLs, dendritic cells, and B cells. Day 3 brings pDCs and T helper cells. On day 5, our model predicts IL-10 and IL-12 induction, although the data suggest that these cytokines remain at baseline levels. Finally, day 7 brings the antibodies, but the virus titer has remained high for so long that the host succumbs to infection.
(ii) Optimized model for older mice.
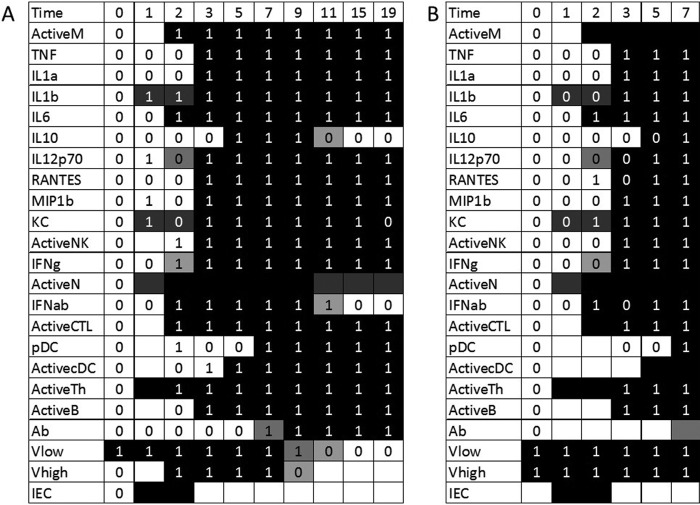
The rules modeling the older mice simulate the data with 94% accuracy, generating 18 total model errors for the 306 data points. Table 1 lists the summary of 384 rule combinations used to generate these simulations. There are multiple rule sets that yield 18 model errors, and as such, not every rule set will produce an identical simulation, although the total number of errors is identical. Figure 2 shows the output of these solutions. Darker gray squares represent a greater likelihood that each model will predict that a variable is turned on at that point, and lighter gray squares indicate a greater likelihood that the rule predicts that a variable will be turned off.
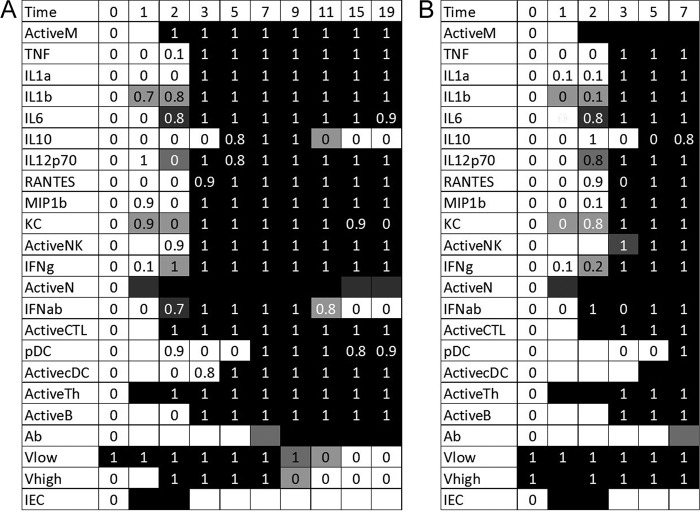
FIG 2.
Optimal fits to the full data set for older mice in sublethal (A) and lethal (B) simulations. Experimental data are indicated with 0's and 1's. Variables for which no data were measured are indicated with a blank cell. The simulated trajectories are indicated by the shading of the table cell, where a black cell represents a variable predicted to have a value of 1 at that time point and a white cell represents a variable predicted to have a value of 0. Thus, if a black cell overlaps a value of 1, the simulation correctly predicts that variable's trajectory at that point. A white cell overlapping a value of 0 is also a correct prediction. Blank cells can predict a value of either 0 or 1 without penalty. A total of 18 data points are missed in the optimal fit.
On day 1, epithelial cells become infected by the virus, and CD4+ T cells become activated and move to the site of infection. In some simulations, IL-1β, KC, and neutrophil levels also increase in the lungs on day 1. On day 2, the levels of macrophages, IL-6, type I interferon, and CTLs are then increased in all simulations, and IL-12 and type II interferon levels are increased in some simulations. Macrophages then cause increases in the levels of most cytokines and chemokines, as well as activating B cells, via their role as antigen-presenting cells. In response to the increased inflammatory response on day 3, IL-10 is upregulated significantly on day 5. Dendritic cells are also brought in on day 5, and pDCs are delayed until day 7. This is in contrast to younger mice, in which dendritic cells were activated on days 2 and 3. The data also show a quick state change in pDCs on day 2, followed by a decrease on days 3 and 5 and then an increase again on day 7. The day 2 data point is likely an anomaly in the data, and our model tends to ignore this point in the rule choices.
Antibodies are upregulated on either day 7 or 9 and clear the virus from the system on day 9 or 11, depending on the rule chosen. Once the virus is removed, type I interferon, IL-10, and, in some cases, neutrophils, return to their baseline levels. The values for all other variables remain elevated on day 19, implying that the immune system has not yet recovered from infection. In the data, the KC level also decreased to its baseline level, but our rules miss this transition.
In the lethal case (Fig. 2B), the simulations were identical to the first 7 days of the sublethal simulation, demonstrating that the high level of virus present initially did not have an effect on the strength of the immune response. Elderly hosts have been shown to exhibit slow responses to virus (5, 21).
(iii) Differences in rule choices for young and old mice.
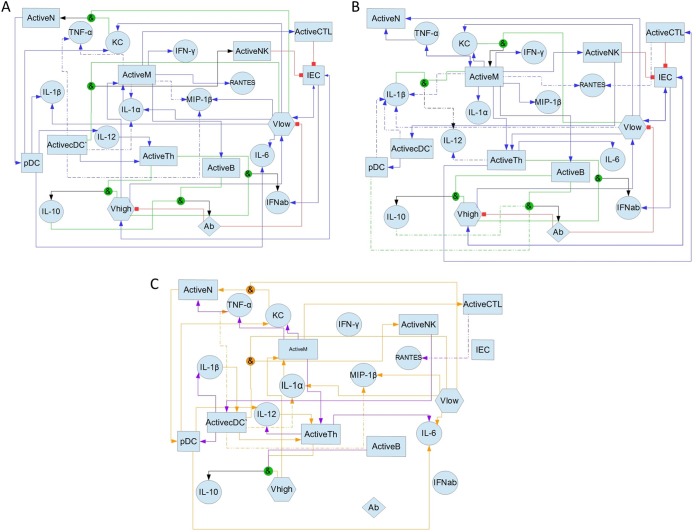
Because the data generally differed between age groups in both activation and deactivation for most variables in the model, most variables were governed by distinct rules. Figure 3C denotes the variables that are regulated by different rules between the two age groups. Many of these distinctions involve differences in the dependence on the virus; in younger mice, many variables responded to the presence of the virus, while in the older mice, only a few variables did so. Cytokines and chemokines with a direct dependence on the virus were significantly produced by epithelial cells in the host.
FIG 3.
Network diagram of optimal rule choices for the Boolean model fitted to the full data set. (A) Diagram of rule choices for the full data set for younger mice. Blue arrows indicate a direct relation between two components. More than one blue arrow pointing toward a variable indicates an “or” condition. Green lines indicate two or more components that activate another component through an “and” operator. Black arrows indicate the output of the “and” operator. Red blunted arrows indicate a “not” condition. Rectangles represent cell populations, circles represent cytokines and chemokines, hexagons represent viral loads, and the diamond represents antibodies. Dashed lines represent rule alternatives that exist in some, but not all, models that comprise the optimal solution. (B) Diagram of rule choices for older mice. Lines and shapes are as described above for panel A. (C) Differences in rule choices between age groups. Orange arrows represent rules seen in the younger-mouse model but not in the older-mouse model. Purple arrows represent rules seen in the older-mouse model but not in the younger-mouse model. Shapes without incoming arrows have identical rules between age groups.
Activated macrophages were the cellular source of many cytokines and chemokines in both young and old mice. Younger mice also tended to have an additional, equivalent rule in which these cytokines were produced by activated dendritic cells. In both our simulations and the data, macrophages and dendritic cells become activated at the same time in younger mice. Dendritic cells did not have this same effect in older mice, as they become activated 1 to 2 days later than macrophages. Panda et al. showed previously that dendritic cells were unable to respond to influenza virus with the same efficacy in older mice as in younger mice, and they exhibited decreased production of TNF, IL-6, and IL-12 (22). In our model, dendritic cells from older mice were unable to significantly contribute to the production of many of the cytokines, including those identified in the work by Panda et al. In fact, in older mice, dendritic cells are responsible for the production of the chemokine KC only.
Dysregulation of cytokine production can also lead to defects in the antibody response to influenza (22), which in turn can lead to a decrease in the efficacy of the antiviral response of the host. The data from experiments with older mice indicate that the virus remains in the host 2 days longer than it remains in younger mice. The lengthened infection period leads to excess symptoms in older mice (19). This may also account for some of the increased morbidity and mortality seen in older hosts in response to viral infection (19, 23).
Consensus rule sets and rule robustness.
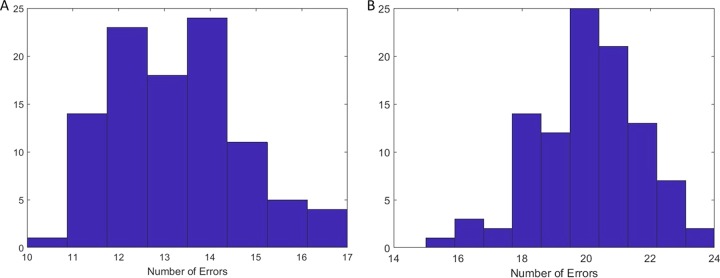
Figure 4 shows the distribution of model errors associated with the bootstrap consensus rule sets for younger and older mice. The younger bootstrap replicates led to an average error value of 13.2, with a minimum of 10 and an interquartile range (IQR) of 12 to 14 (Fig. 4A). The older bootstrap replicates had an average error value of 20.1, with a minimum of 15 and an IQR of 19 to 21 (Fig. 4B).
FIG 4.
Error distributions for bootstrap replicate outputs. Shown are distributions of model errors for bootstrap replicates for younger mice (4,607 models) (A) and older mice (30,072 models) (B).
As with the original data set, each of the bootstrap replicates had multiple optimal rule sets with different rules. For the younger mice, we generated 4,607 rule sets, and for the older mice, we generated 30,072 rule sets in total for the 100 data sets tested. Table 2 summarizes the rule choices between age groups, indicating the percentages of rule sets that include a particular rule for the full set of bootstrap outputs. Figures 5 and 6 show the average fit of the models generated in the bootstrap experiment. Numbers represent the average values of the data for a particular variable on each day. Figure 5 shows the bootstrap output for younger mice, and Fig. 6 shows the output for older mice. In all variables, the frequency of a particular rule choice aligned well with what the optimal solution suggests (Table 2). Thus, we conclude that our model was robust and that our rules did not overfit the original data set.
TABLE 2.
Bootstrapping rule choices for younger and older mice
| Rule | % of models using rule |
|
|---|---|---|
| Younger mice | Older mice | |
| ActiveM ← (KC & Vlow) | TNF | 0.0 | 99.9 |
| ActiveM ← Vhigh | IL1a | 100.0 | 0.1 |
| TNF ← ActiveM | Vhigh | 53.2 | 1.3 |
| TNF ← ActivecDC | Vhigh | 46.8 | 1.3 |
| TNF ← ActiveM | 0.0 | 97.4 |
| IL1a ← ActiveM | Vlow | 50.3 | 0.1 |
| IL1a ← ActiveM | 0.0 | 99.9 |
| IL1a ← ActivecDC | Vlow | 49.7 | 0.1 |
| IL1b ← ActiveM | Vlow | 50.1 | 21.6 |
| IL1b ← ActiveM | 0.3 | 35.0 |
| IL1b ← ActivecDC | Vlow | 49.6 | 21.7 |
| IL1b ← pDC | Vlow | 0.0 | 21.7 |
| IL-6 ← ActiveM | Vlow | 45.2 | 0.0 |
| IL-6 ← ActiveM | 0.0 | 20.3 |
| IL-6 ← ActiveTh | 0.0 | 79.7 |
| IL-6 ← ActivecDC | Vlow | 44.8 | 0.0 |
| IL-6 ← pDC | Vlow | 10.0 | 0.0 |
| IL-10 ← ActiveTh & Vhigh | 75.9 | 0.7 |
| IL-10 ← ActiveNK & Vhigh | 24.1 | 49.7 |
| IL-10 ← ActiveB & Vhigh | 0.0 | 49.6 |
| IL12p70 ← ActiveTh & Vhigh | 36.1 | 0.5 |
| IL12p70 ← ActiveTh | 2.1 | 64.3 |
| IL12p70 ← ActiveM & IL1b | 0.0 | 35.2 |
| IL12p70 ← pDC | 61.8 | 0.0 |
| RANTES ← ActiveM | 66.7 | 49.3 |
| RANTES ← ActivecDC | 27.2 | 0.0 |
| RANTES ← ActiveCTL | 6.1 | 50.7 |
| MIP1b ← ActiveM | Vlow | 48.4 | 4.5 |
| MIP1b← ActiveM | 3.5 | 91.1 |
| MIP1b ← ActivecDC | Vlow | 48.1 | 4.5 |
| KC ← ActiveM | Vlow | 3.1 | 50.0 |
| KC ← Vlow | pDC | 96.9 | 50.0 |
| ActiveNK ← ActiveM | 0.0 | 99.3 |
| ActiveNK ← ActiveM & Vlow | 60.5 | 0.7 |
| ActiveNK ← ActivecDC & Vlow | 39.5 | 0.0 |
| IFNg ← ActiveM | 100.0 | 100.0 |
| ActiveN ← Vlow | TNF | 0.0 | 50.0 |
| ActiveN ← KC & Vlow | 100.0 | 50.0 |
| IFNab ← (ActiveTh & Vhigh) | IEC | 100.0 | 100.0 |
| ActiveCTL ← ActiveM | 100.0 | 1.6 |
| ActiveCTL ← ActiveTh | 0.0 | 98.4 |
| pDC ← ActivecDC | 0.0 | 100.0 |
| pDC ← ActiveN | 100.0 | 0.0 |
| ActivecDC ← ActiveNK | 7.3 | 82.5 |
| ActivecDC ← IL1b | 92.7 | 17.5 |
| ActiveTh ← Vlow | ActiveM | 0.0 | 100.0 |
| ActiveTh ← RANTES & ActiveM | 19.7 | 0.0 |
| ActiveTh ← ActivecDC | IL12p70 | 80.3 | 0.0 |
| ActiveB ← ActiveM | 100.0 | 100.0 |
| Ab ← (ActiveB & pDC) | Ab | 0.0 | 28.2 |
| Ab ← (ActiveB & IL-10)| Ab | 100.0 | 71.8 |
| Vlow ← (IEC | Vlow | Vhigh) & ∼(Ab & ∼IL-10) | 0.0 | 36.3 |
| Vlow ← (IEC | Vlow | Vhigh) & ∼(Ab) | 100.0 | 63.7 |
| Vhigh ← (IEC | Vhigh) & ∼(Ab) | 100.0 | 100.0 |
| IEC ← (Vlow | Vhigh) & ∼ActiveCTL & ∼ActiveNK | 100.0 | 100.0 |
FIG 5.
Output from the bootstrap experiments for younger mice. Average values of bootstrap data are indicated by numbers, and the simulated trajectories are indicated by shading, where a black cell represents a variable predicted to have a value of 1 at that time point and a white cell represents a variable predicted to have a value of 0. Gray shading indicates that a variable is “on” at that point for some, but not all, rule sets. Darker gray shading indicates a greater likelihood of a variable having a value of 1 at that point. NaN, component not measured at this time point.
FIG 6.
Output from the bootstrap experiments for older mice. Average values of bootstrap data are indicated by numbers, and the simulated trajectories are indicated by shading, where a black cell represents a variable predicted to have a value of 1 at that time point and a white cell represents a variable predicted to have a value of 0. Gray shading indicates that a variable is “on” at that point for some, but not all, rule sets. Darker gray shading indicates a greater likelihood of a variable having a value of 1 at that point.
Effect of deletion of immune system components on viral clearance.
We tested the effect of removing certain elements of the immune response in silico. For each age group, one variable was kept at its baseline level for all steps of the simulation under sublethal conditions. All models identified by the bootstrap replicates were tested under these conditions, and the average results for each age group are summarized in Table 3. In a previous paper (24), we tested an ordinary differential equation (ODE) model of the immune response to influenza virus infection using the experimental data for younger mice only. In that paper, we tested the model's prediction of the intrahost immune response under sublethal conditions with several elements of the inflammatory response knocked out. The Boolean model knockouts are compared to the ODE model in Table 3.
TABLE 3.
Effect of deletion of immune components on virus clearance in younger and older mice
| Component kept at baseline | ODE model result for younger mice | Boolean model result for younger mice |
|---|---|---|
| IL-10 | Virus is cleared 2 days faster | Virus is not cleared |
| NK cells | Virus is not cleared | Virus is not cleared in 15% of simulations |
| Antibodies | No significant change in virus clearance | Virus is not cleared |
| All inflammation | Virus is not cleared | Virus is not cleared |
The removal of IL-10 from the system prevents the virus from being cleared from the system. Without IL-10 being present, antibody levels do not increase, and the level of the virus remains elevated for the full course of the simulation. IL-10 has been shown in experiments to induce the differentiation of B cells to plasma cells, which in turn produce antibodies (25). In our ODE model, IL-10 functioned as an anti-inflammatory mediator but did not have a direct impact on the adaptive immune response, as it did in the Boolean models. An IL-10 deletion in the ODE model caused the virus to be cleared 2 days sooner than in an experiment with IL-10 (26). It is likely that an IL-10 deletion has a complex effect on the host, which can be either protective or injurious, depending on both the host and the pathogen (27, 28).
We next removed NK cells from the system and tested the effect of their deletion from the host. In our Boolean model, NK cells had different effects on each age group. Without NK cells, younger mice were still able to clear the virus fully from the system in about 85% of simulations. NK cells predominantly clear infected cells, but CTLs have a redundant role in clearing infected cells. CTLs kill the cells independently, leading to viral clearance. This result differs from the results of the ODE model, in which an NK cell knockout kept the virus from being cleared and forced the level of infected cells to stay elevated for a longer time.
In older mice, NK cells were important for the clearance of infected cells and had an additional role in aiding in the production of IL-10 (29). Without NK cells, older mice will not produce significant amounts of IL-10, which will limit antibody production as well. Without antibodies, the virus cannot be cleared from the system. Numbers of NK cells have been shown to increase as we age (30), so their loss may have been felt more strongly in older mice.
The removal of antibodies keeps the virus from being cleared in both Boolean models, consistent with biological evidence (31). In the ODE model, virus was cleared even without an increase in the levels of antibodies (our unpublished data). Infected cells were cleared quickly, removing the source of new virus from the system. Without a large production of the virus, the innate responses cleared the virus relatively easily, although this may not reflect how the virus acts in vivo. The Boolean models better reflect the necessity of antibodies for survival of viral infection.
The bottom row of Table 3 demonstrates the models' responses when macrophages, cytokines, and chemokines have all been removed from the system. The removal of all these inflammatory components from the model has a largely deleterious effect on the host. In all three model simulations, the virus cannot be cleared from the system without the onset of inflammation, and numbers of infected cells peaked at higher levels and for longer times than with this arm of the immune system in place.
DISCUSSION
Immunosenescence in humans has to date remained a poorly understood phenomenon. Changes in the immune system of healthy older patients can be difficult to ascertain given the wide range of interpatient variability seen in human subjects as well as the complex system of interactions between immune components. Discrete, rule-based models allow the data-driven discovery of important interactions between components of the host-virus response to influenza virus infection in a way that may be more robust to interpatient variability than other modeling approaches, such as ODEs. Most previously reported Boolean models of the immune response to infection focus exclusively on the analysis of steady-state conditions and do not leverage available dynamical data (15–18); our model, however, looked at a rich set of time series data to which the outputs of the model are matched. The modeling framework developed here (Boolean model combined with linear-programming optimization of the rule set to match observed data) is easy to apply to other scenarios, and the data-fitting process is computationally inexpensive.
Rule-based models allow an intuitive interpretation of the interactions between variables, making them simpler for nonexperts to understand and apply. The rules allow a representation of complicated biological phenomena with a straightforward combination of “ors,” “ands,” and “nots.” Rule-based models also allow the discovery of novel interactions between components of the model.
In comparing activation data between young and old mice, it is clear that there must be a shift in the cellular source of many cytokines and chemokines as we age. The Boolean data show that the levels of activated macrophages increase on day 2 for both younger and older mice. There is disagreement in the literature over how macrophage populations change as we age: some papers report a decrease in bone marrow macrophage counts (32, 33), whereas other papers suggest an increase (34). Defects have also been reported for Toll-like receptors (TLRs) on macrophage surfaces (2), which may diminish their ability to react to an infection and affect the numbers of macrophages found in tissues during experiments. Our data suggest that age presents no difference in the recruitment of macrophages to the site of infection, but there is a difference in cytokine expression in these cells.
Cytokine dysregulation plays an important role in the rule choices for older mice. Almost every cytokine and chemokine is regulated by rules different from those used in the younger-mouse model. In particular, older mice are less likely to have inflammatory components respond directly to the virus, representing an initial upregulation by lung epithelial cells. Dysregulation of the lung epithelium may account for the slower initiation of many immune responses in older hosts, in whom the inflammatory response has been shown to be delayed by about 2 days (19).
Our rules imply that both type I and type II interferons were regulated via the same mechanisms in older and younger mice. Both age groups rely on monocytes to produce gamma interferon (IFN-γ) (35). The rule for IFN-α/β production is slightly more complex, as it needs to match both an increase early in infection and a decrease late in the simulation. In our model, IFN-α/β is produced primarily by infected epithelial cells and CD4+ T cells. Although T cells may not produce interferon directly, their presence may prime other cells, such as plasmacytoid dendritic cells, to produce interferon. We cannot model this directly, as the Boolean-valued data for dendritic cells cannot adequately represent this interaction, so we utilize T helper cells in the rule instead.
B cells were also regulated by the same rules in young and old mice. Although their function and effect on other components of the model may vary, the Boolean data revealed enough similarity in the B cells that they could agree on rule choices. This implies that the differences in activation and recruitment in the innate immune response are more substantial than those in the B cell responses in this model.
Some of our results might have been improved with a richer data set. Some variables of this model, such as neutrophils and epithelial cells, did not have accompanying data to which we could match our trajectories. Data for other variables, like antibodies and macrophages, were available for some but not all cohorts. Numbers of cells were not measured on every day of the experiment, causing several missing data points, at which times our model could predict a cell to be “on” or “off” without penalty. Adding to this data set may have strengthened our predictions by removing this ambiguity. We are also unable to obtain truly longitudinal data for a mouse model of influenza, as mice must be sacrificed in order to measure the data (24). These trajectories then had to be reconstituted from pooled data from three different animals sacrificed at each time point. Results might have been further improved if we had been able to track a single animal over the full course of infection. We initiated the optimization process for rule set identification from a superset of potential rules derived from the literature and obvious patterns seen in data. It might have been preferable to infer a universe of potential rules entirely from data, starting from a comprehensive set of all possible rules given a preset level of rule complexity. We are currently looking into efficient ways to compute this superset. We used bootstrapping to mitigate overfitting and thus assess the robustness of the rule sets inferred from the data. Eliminating data from individual animals seemed the most intuitive method of creating subsets of data but also introduced the necessity of recomputing 0's and 1's in these subsets. This is a much more stringent requirement than simply eliminating 0's and 1's randomly from the complete data set. To our knowledge, there are no established methods to assess rule set robustness in situations such as ours, where the source data themselves are not binary.
Hernandez-Vargas et al. previously studied a portion of these influenza virus infection data for young and old mice (36). Using a small, target cell-limited ODE model, those authors fit data for the virus levels in both age groups. They determined that type I interferon, type II interferon, and TNF have redundant roles in mediating antiviral effects postinfection, but they did not consider the different mechanisms by which each of these cytokines helps the host to fight infection. Our model incorporates many more mechanisms, and as such, we can capture information about dysregulation in the activation and recruitment of cells and cytokines, which tend to vary greatly between age groups. In our Boolean model, TNF and interferon do not have redundant roles. TNF acts as a proinflammatory cytokine to increase the presence of macrophages and neutrophils, and it can be upregulated by dendritic cells, macrophages, or epithelial cells. Interferon helps to prevent the spread of the virus from infected to uninfected cells. Because our data do not include counts of infected cells, we do not model this explicitly. Hernandez-Vargas et al. also did not find an important effect of NK cells in improving the fits of their model to the experimental data. Our model, however, presents an important role for NK cells, particularly in the simulations with older mice. Numbers of NK cells have been shown to increase greatly with age, likely to compensate for a deficiency in CTLs in older hosts (30). The greater complexity represented in our model with 20 more components allows our model to demonstrate the importance of some specific pieces of the immune response that a simpler model may not be able to reveal.
In conclusion, we present an application of optimization methods to compute rule-based Boolean network models of murine influenza A virus infection, based on rich, multivariate time series experimental data with sublethal and lethal inocula in young and old mice. Our model emphasizes rule differences, mapping to biological differences between younger and older hosts, supporting some documented mechanisms of immunosenescence. Importantly, the Boolean network also led to the suggestion of alternative data-driven mechanisms, like those of IL-10, which could guide further focused experimental work on uncovering the biological bases of immunosenescence.
MATERIALS AND METHODS
Experimental data.
Data to which the model is calibrated were measured in BALB/c mice subjected to influenza A virus infection, a subset of which was presented previously (19, 24). Mice were of one of two age groups: young mice, 12 to 16 weeks of age, or old mice, 72 to 76 weeks of age. Within each of these age groups, mice were further subdivided into two cohorts based on the initial viral inoculum: sublethal (50 PFU dose) or lethal (500 PFU) (19). In the sublethal cohort, data were obtained on days 0, 1, 2, 3, 5, 7, 9, 11, 15, and 19. In the lethal cohort, data were collected on days 0, 1, 2, 3, 5, and 7, at which point the remaining mice succumbed to infection. At each time point, at least three mice were sacrificed for the data measurements, and from these mice, we generated a mean and standard deviation of each measurement. We used these statistics to transform the data from real-valued measurements to Boolean values. Using day 0 measurements as a common baseline (a total of 12 measurements, 6 for each initial dose), we performed analysis of variance (ANOVA) to test if a data point for variable X at time T is significantly larger than the value of variable X at baseline (P < 0.05). We then applied a post hoc correction to the ANOVA output to account for the many t tests required. We used Dunnett's test, which corrects for multiple comparisons to a single control (37). If a significant difference is observed, variable X is assigned a value of 1 at time T (to denote an elevated level); otherwise, the variable is assigned a value of 0. (There were no instances in which a variable would attain a value significantly lower than its day 0 baseline value.) We repeated this process for all variables across all cohorts, yielding the Boolean-valued data points to which the model is calibrated. We have 310 data points for the younger mice and 306 data points for the older mice.
The virus is considered to be “on” until the immune system clears it. Initially, sublethal infection has a low level of the virus, and lethal infection has a high level of the virus. Virus is the only component in the system that begins with a data point of 1, indicating that it is initially present at an elevated level, causing infection. A viral titer of between 50 PFU and 500 PFU is considered a low virus level, and any viral titer above 500 PFU is considered a high virus level. Once the level of the virus is below 50 PFU, it falls below the lower limit of detection, and we consider it to be cleared from the system (a data point of 0).
Modeling framework.
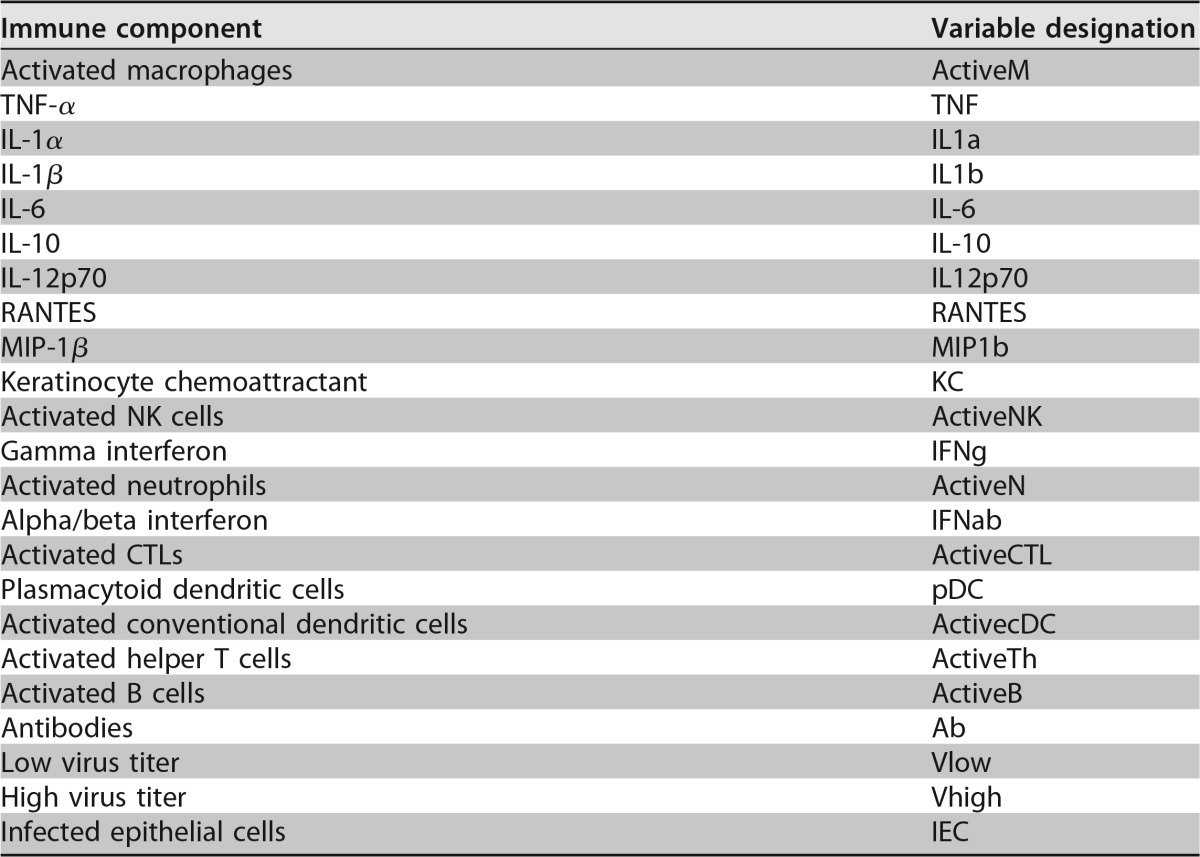
We have constructed a rule-based model of the immune response to influenza virus infection, which accounts for 23 variables representing the viral load, immune cells, cytokines, chemokines, antibodies, and infected epithelial cells (Table 4). The library of potential interactions and relations between the model variables is inferred from data in the existing literature and then refined by using our experimental data. The alternative outcomes of a modeled infection are either viral clearance or death of the host, depending on the inoculum.
TABLE 4.
Variables and associated abbreviations for the Boolean network model
The model is a strict two-state Boolean model, with each variable attaining two values, 0 (at or near baseline values) or 1 (significantly above baseline values). The values of the variables change synchronously at discrete time points that are not necessarily equally spaced in time, to allow variable rates of switching processes. These changes are governed by a Boolean rule, which defines the conditions under which the variable should take on a value of 1 at the next step based on the current values of other variables. These rules are relatively simple and involve a combination of “and,” “or,” and “not” operators (also denoted &, ∣, and ∼, respectively). For example, if two or more components are required for the activation of a variable, the rule will include an “and” operator (e.g., in the rule “ActiveN ← KC & Vlow,” both KC and a low level of virus are required to activate neutrophils). If one of multiple sources is sufficient to activate a variable, this rule will include an “or” operator (e.g., in the rule “IL1b ← ActiveM ∣ Vlow,” an elevation of the IL-1β level requires either activated macrophages or a low level of the virus). If one component inhibits another, the rule will include a “not” operator (e.g., in the rule “Vhigh ← [IEC ∣ Vhigh] & ∼Ab,” the increase of the virus to a high level requires the absence of antibodies and either the presence of infected cells or an already elevated level of the virus). Because the two age groups feature distinct patterns in their data sets (in particular, there is a 1- to 2-day delay in the onset of many inflammatory components), we use distinct rule sets to model each age group's response to infection. Calibration of the model, which consists of selecting the rules for inclusion in the transfer functions, allows us to capture the data-driven differences in immune responses between the age groups and provide conclusions on the impact of immunosenescence on the immune response to influenza virus infection.
To assemble the rules of the Boolean model, we first generated a library of potential rules for each of the 23 variables based on data available in the literature that included various observed or hypothetical interactions between the model variables. For example, the proinflammatory cytokine TNF can be produced by neutrophils (38), macrophages (39), dendritic cells (40), and epithelial cells (41). The time at which TNF transitions from a value of 0 to a value of 1 dictates which of these potential producers will be most influential in its trajectory. Thus, choices for TNF rules included combinations of these cells. Rule choices were generated primarily from the literature, but some are also data driven. Rules are kept simple in that no more than five variables were involved in any particular rule. Data from both younger and older mice were fit from the same library of 68 total rule choices.
Optimization of rule choices.
To find the optimal set of Boolean rules that best described the data, we reformulated the rule discovery problem into a mixed-integer linear-programming (MILP) problem. A similar formulation was reported previously by Atias et al. (42). We define our objective function as the minimum difference between the model trajectory and the measured data, as given by equation 1. This was reformulated as a linear objective function using dummy variables (see equation A1 in the Appendix for details). Dt,s and Mt,s represent the measured data and model, respectively, for state s at time t.
| (1) |
All potential Boolean rules were expressed as a series of logical equivalences (if and only if statements P1 ↔ P2). These rules were expanded into their equivalent conjunctive normal form, which can be expressed as a series of independent or constraints, each of which can be represented as a single linear inequality (43). As long as each of these linear inequalities is satisfied, the overall conjunction expression is satisfied. The result is
| (2) |
| (3) |
| (4) |
where yij represents the Boolean value of the expression Pij and DV is a Boolean decision variable. The decision variable allows the optimizer to apply this constraint (DV = 1) or turn it off (DV = 0). Additional formulation details are provided in the Appendix.
A Python (version 3.5) package was written to accept Boolean data and a list of potential rules for each state. This package reformulates the inputs into an MILP problem for use with the Python Optimization Modeling Objects package (Pyomo) (44, 45). Pyomo converts this script into a solver-friendly file, which was solved by using the IBM ILOG CPLEX optimization studio. CPLEX was set to populate all optimal solutions via its solution pool feature. Finally, our Python package parses through this solution pool and generates the rule selection frequency identified in Results.
Network simulation.
The Boolean network was simulated with the Python package. Model error is defined as the total number of data points incorrectly predicted by the simulation. Each time step represents a jump from one state of the system to the next, rather than a fixed time interval. In this way, we capture all state changes that occur in each variable as defined by a change in a variable from a 0 to a 1 or from a 1 to a 0 but potentially ignore differences between cohorts in the finer timing of changes in states.
We simulate the system with synchronous updates for 6 time steps for the lethal cohort and 10 time steps for the sublethal cohort. At time zero, only the virus is set to a value of 1; all other variables are considered “off” initially. In the sublethal simulations, only Vlow is “on” initially, whereas in the lethal simulations, both Vlow and Vhigh are “on” initially. Within each age group, sublethal and lethal cohorts are simulated with the same set of rules; only the initial condition is changed.
Building a consensus rule set.
None of the classical averaging techniques apply to our specific task of building a consensus rule set for each cohort (46–48). We therefore proceeded as follows. We generated 100 new data sets by removing randomly 10% of the raw data (making sure that at least two data points remain at each time point for each variable) and recalculating the Boolean levels for each of the 23 variables. Optimization of the set of rules was performed for each bootstrap data set in the same way as for the full data set. Generally, multiple rule sets were found to give the same optimal predictive accuracy. The consensus bootstrap rule set was obtained by creating, for each variable, a disjunctive rule assembling each rule emerging from the optimal rule sets.
APPENDIX
To fit the Boolean data, we find the optimal set of rules that fit the data with the fewest total errors. We begin with a library of 68 possible rule choices (Table A1). We generate a separate set of rules for older and younger mice, but only one rule set is used to model the sublethal and lethal data within one age group. To obtain these rule sets, we reformulated the rule discovery problem into an integer linear-programming problem (42, 49). The objective function is the minimized difference between the model prediction and the measured data. The objective was then linearized by using dummy variables, At,s, given by the equation
| (A1) |
where Dt,s and Mt,s represent the measured data and model, respectively, for state s at time t.
TABLE A1.
Library of rule choices
| Rule choice |
|---|
| ActiveM ← (KC & Vlow) | TNF |
| ActiveM ← Vhigh | IL1a |
| ActiveM ← IL1a | ActiveN |
| TNF ← ActiveM | Vhigh |
| TNF ← ActivecDC | Vhigh |
| TNF ← ActiveM |
| IL1a ← ActiveM | Vlow |
| IL1a ← ActiveM |
| IL1a ← ActivecDC | Vlow |
| IL1b ← ActiveM | Vlow |
| IL1b ← ActiveM |
| IL1b ← ActivecDC | Vlow |
| IL1b ← pDC | Vlow |
| IL-6 ← ActiveM | Vlow |
| IL-6 ← ActiveM |
| IL-6 ← ActiveTh |
| IL-6 ← ActivecDC | Vlow |
| IL-6 ← pDC | Vlow |
| IL-10 ← ActiveTh & Vhigh |
| IL-10 ← ActiveNK & Vhigh |
| IL-10 ← ActiveB & Vhigh |
| IL12p70 ← ActiveTh & Vhigh |
| IL12p70 ← ActiveTh |
| IL12p70 ← ActiveM & IL1b |
| IL12p70 ← pDC |
| RANTES ← ActiveM |
| RANTES ← ActivecDC |
| RANTES ← ActiveCTL |
| MIP1b ← ActiveM | Vlow |
| MIP1b← ActiveM |
| MIP1b ← ActivecDC | Vlow |
| KC ← ActiveM | Vlow |
| KC ← ActiveM |
| KC ← Vlow | pDC |
| ActiveNK ← ActiveM |
| ActiveNK ← ActiveM & RANTES |
| ActiveNK ← ActiveM & Vlow |
| ActiveNK ← ActivecDC & Vlow |
| IFNg ← (ActiveM) |
| IFNg ← ActiveN |
| ActiveN ← Vlow | TNF |
| ActiveN ← KC & Vlow |
| IFNab ← ActiveNK |
| IFNab ← (ActiveTh & Vhigh) | (IEC & Vhigh) |
| IFNab ← (ActiveTh & Vhigh) | IEC |
| ActiveCTL ← ActiveM |
| ActiveCTL ← ActiveTh |
| pDC ← ActivecDC |
| pDC ← ActiveN |
| ActivecDC ← ActiveNK |
| ActivecDC ← Vlow | Ng |
| ActivecDC ← IL1b |
| ActiveTh ← Vlow | ActiveM |
| ActiveTh ← RANTES & ActiveM |
| ActiveTh ← ActivecDC | IL12p70 |
| ActiveB ← ActiveM |
| Ab ← (ActiveB & pDC) | Ab |
| Ab ← (ActiveB & IL-10)| Ab |
| Vlow ← (IEC | Vlow | Vhigh) & ∼(Ab & ∼IL-10) |
| Vlow ← (IEC | Vlow | Vhigh) & ∼(Ab) |
| Vhigh ← (IEC | Vhigh) & ∼(Ab) |
| IEC ← (Vlow | Vhigh) & ∼ActiveCTL & ∼ActiveNK |
Formulation of Boolean rules.
All Boolean rules can be expressed in the conjunctive normal form, which is comprised of a series of “and” clauses: rule R = Q1 ∧ Q2 ∧ … ∧ QN, where Qi is a series of inclusive “or” terms, Qi = P1 ∨ P2 ∨ … ∨ PM (43). Each term P is the name of a variable in the system with or without a “not” operator preceding it, depending on whether the term has a positive or negative effect on the clause.
Let yi represent the Boolean value of Pi. Each of the Qi logical “or” constraints can be expressed as
| (A2) |
In other words, at least one yi value must be 1 for the “or” constraint to be satisfied. The “and” constraint, R, does not need to be explicitly stated because equation A2 ensures that each subclause, Qi, is true, and if R is comprised of a series of true clauses, R must be satisfied.
The “not” clauses, ¬Pi, can be expressed as 1 − yi. Implications, e.g., P1 ⇒ P2, can be expressed as ¬P1 ∨ P2, which is an “or” constraint:
| (A3) |
Using this framework, we can formulate this as an MILP problem (42, 49). Potential rules are always of the form Si,t+1 ← St, where St represents a series of logical operations acting upon state s at current time t. This logical clause will generate an update in the ith state Si at time t + 1. If this rule were true, Si,t+1 ⇔ St for all time, t. Applying the above-described equivalences, we obtain
| (A4) |
| (A5) |
which we expand into the conjunctive normal form and apply the appropriate linear constraints.
Finally, to perform rule optimization, Boolean decision variables, Dij, are initialized for every rule j at each state i. The k “or” constraints generated from the conjunctive normal form of the ijth rule are now represented as
| (A6) |
Here we modify the rule laid out in equation A2 to allow the optimizer to turn a rule on or off, depending on how well it fits the experimental data. If the decision variable Dij is 0, the values of yi are unconstrained, and potential rule ij does not apply. If Dij is 1, the rule applies. A final constraint is set such that each state may have only 1 rule selected:
| (A7) |
Now we look at a detailed example of constraint formation from an example potential rule: ActiveM(t + 1) ← KC(t) ∧ IL-6(t). This rule is equivalent to the following constraints:
| (A8) |
| (A9) |
| (A10) |
| (A11) |
| (A12) |
REFERENCES
- 1.Centers for Disease Control and Prevention. 2006. Prevention and control of influenza: recommendations of the Advisory Committee on Immunization Practices (ACIP). MMWR Morb Mortal Wkly Rep 55:1–42.16410759 [Google Scholar]
- 2.Plowden J, Renshaw-Hoelscher M, Engleman C, Katz J, Sambhara S. 2004. Innate immunity in aging: impact on macrophage function. Aging Cell 3:161–167. doi: 10.1111/j.1474-9728.2004.00102.x. [DOI] [PubMed] [Google Scholar]
- 3.Population Division, Department of Economic and Social Affairs, United Nations. 2001. World population ageing: 1950–2050. United Nations, New York, NY. [Google Scholar]
- 4.Franceschi C, Bonafè M, Valensin S. 2000. Human immunosenescence: the prevailing of innate immunity, the failing of clonotypic immunity, and the filling of immunological space. Vaccine 18:1717–1720. doi: 10.1016/S0264-410X(99)00513-7. [DOI] [PubMed] [Google Scholar]
- 5.Ginaldi L, Loreto MF, Corsi MP, Modesti M, De Martinis M. 2001. Immunosenescence and infectious diseases. Microbes Infect 3:851–857. doi: 10.1016/S1286-4579(01)01443-5. [DOI] [PubMed] [Google Scholar]
- 6.Shaw AC, Goldstein DR, Montgomery RR. 2013. Age-dependent dysregulation of innate immunity. Nat Rev Immunol 13:875–887. doi: 10.1038/nri3547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Franceschi C, Bonafè M, Valensin S, Olivieri F, De Luca M, Ottaviani E, De Benedictis G. 2000. Inflamm-aging. An evolutionary perspective on immunosenescence. Ann N Y Acad Sci 908:244–254. doi: 10.1111/j.1749-6632.2000.tb06651.x. [DOI] [PubMed] [Google Scholar]
- 8.Krone CL, Trzciński K, Zborowski T, Sanders EAM, Bogaert D. 2013. Impaired innate mucosal immunity in aged mice permits prolonged Streptococcus pneumoniae colonization. Infect Immun 81:4615–4625. doi: 10.1128/IAI.00618-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mancuso P, McNish R, Peters-Golden M, Brock T. 2001. Evaluation of phagocytosis and arachidonate metabolism by alveolar macrophages and recruited neutrophils from F344xBN rats of different ages. Mech Ageing Dev 122:1899–1913. doi: 10.1016/S0047-6374(01)00322-0. [DOI] [PubMed] [Google Scholar]
- 10.De La Fuente M. 1985. Changes in the macrophage function with aging. Comp Biochem Physiol A Comp Physiol 81:935–938. doi: 10.1016/0300-9629(85)90933-8. [DOI] [PubMed] [Google Scholar]
- 11.De La Fuente M, Medina S, Del Rio M, Ferrandez M, Hernanz A. 2000. Effect of aging on the modulation of macrophage functions by neuropeptides. Life Sci 67:2125–2135. doi: 10.1016/S0024-3205(00)00799-2. [DOI] [PubMed] [Google Scholar]
- 12.Weksler MC, Innes JD, Goldstein G. 1978. Immunological studies of aging. IV. The contribution of thymic involution to the immune deficiencies of aging mice and reversal with thymopoietin32-36. J Exp Med 148:996–1006. doi: 10.1084/jem.148.4.996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ferguson FG, Wikby A, Maxson P, Olsson J, Johansson B. 1995. Immune parameters in a longitudinal study of a very old population of Swedish people: a comparison between survivors and nonsurvivors. J Gerontol A Biol Sci Med Sci 50:B378–B382. doi: 10.1093/gerona/50A.6.B378. [DOI] [PubMed] [Google Scholar]
- 14.Meyer KC. 2001. The role of immunity in susceptibility to respiratory infection in the aging lung. Respir Physiol 128:23–31. doi: 10.1016/S0034-5687(01)00261-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Raman K, Bhat AG, Chandra N. 2010. A systems perspective of host-pathogen interactions: predicting disease outcome in tuberculosis. Mol Biosyst 6:516–530. doi: 10.1039/B912129C. [DOI] [PubMed] [Google Scholar]
- 16.Thakar J, Pilione M, Kirimanjeswara G, Harvill ET, Albert R. 2007. Modeling systems-level regulation of host immune responses. PLoS Comput Biol 3:e109. doi: 10.1371/journal.pcbi.0030109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Thakar J, Saadatpour-Moghaddam A, Harvill ET, Albert R. 2009. Constraint-based network model of pathogen-immune system interactions. J R Soc Interface 6:599–612. doi: 10.1098/rsif.2008.0363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Thakar J, Pathak AK, Murphy L, Albert R, Cattadori IM. 2012. Network model of immune responses reveals key effectors to single and co-infection dynamics by a respiratory bacterium and a gastrointestinal helminth. PLoS Comput Biol 8:e1002345. doi: 10.1371/journal.pcbi.1002345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Toapanta FR, Ross TM. 2009. Impaired immune responses in the lungs of aged mice following influenza infection. Respir Res 10:112–131. doi: 10.1186/1465-9921-10-112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Matsukura S, Kokubu F, Noda H, Tokunaga H, Adachi M. 1996. Expression of IL-6, IL-8, and RANTES on human bronchial epithelial cells, NCI-H292, induced by influenza virus A. J Allergy Clin Immunol 98:1080–1087. doi: 10.1016/S0091-6749(96)80195-3. [DOI] [PubMed] [Google Scholar]
- 21.Seres I, Csongor J, Mohacsi A, Leovey A, Fulop T. 1993. Age-dependent alteration of human recombinant GM-CSF effects on human granulocytes. Mech Ageing Dev 71:143–154. doi: 10.1016/0047-6374(93)90042-P. [DOI] [PubMed] [Google Scholar]
- 22.Panda A, Qian F, Mohanty S, van Duin D, Newman FK, Zhang L, Chen S, Towle V, Belshe RB, Fikrig E, Allore HG, Montgomery RR, Shaw AC. 2010. Age-associated decrease in TLR function in primary human dendritic cells predicts influenza vaccine response. J Immunol 184:2518–2527. doi: 10.4049/jimmunol.0901022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Castle SC. 2000. Clinical relevance of age-related immune dysfunction. Clin Infect Dis 31:578–585. doi: 10.1086/313947. [DOI] [PubMed] [Google Scholar]
- 24.Price I, Mochan-Keef ED, Swigon D, Ermentrout GB, Lukens S, Toapanta FR, Ross TM, Clermont G. 2015. The inflammatory response to influenza A virus (H1N1): an experimental and mathematical study. J Theor Biol 374:83–93. doi: 10.1016/j.jtbi.2015.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Agematsu BK, Nagumo H, Oguchi Y, Nakazawa T, Fukushima K, Yasui K, Ito S, Kobata T, Morimoto C, Komiyama A. 1998. Generation of plasma cells from peripheral blood memory B cells: synergistic effect of interleukin-10 and CD27/CD70 interaction. Blood 91:173–181. [PubMed] [Google Scholar]
- 26.Brooks DG, Trifilo MJ, Edelmann KH, Teyton L, McGavern DB, Oldstone MBA. 2006. Interleukin-10 determines viral clearance or persistence in vivo. Nat Med 12:1301–1309. doi: 10.1038/nm1492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mege JL, Meghari S, Honstettre A, Capo C, Raoult D. 2006. The two faces of interleukin 10 in human infectious diseases. Lancet Infect Dis 6:557–569. doi: 10.1016/S1473-3099(06)70577-1. [DOI] [PubMed] [Google Scholar]
- 28.Mocellin S, Marincola F, Rossi CR, Nitti D, Lise M. 2004. The multifaceted relationship between IL-10 and adaptive immunity: putting together the pieces of a puzzle. Cytokine Growth Factor Rev 15:61–76. doi: 10.1016/j.cytogfr.2003.11.001. [DOI] [PubMed] [Google Scholar]
- 29.Mehrotra PT, Donnelly RP, Wong S, Geremew A, Mostowski HS, Siegel JP, Bloom ET. 1998. Production of IL-10 by human natural killer cells stimulated with IL-2 and/or IL-12. J Immunol 160:2637–2644. [PubMed] [Google Scholar]
- 30.Solana R, Alonso MC, Pena J. 1999. Natural killer cells in healthy aging. Exp Gerontol 34:435–443. doi: 10.1016/S0531-5565(99)00008-X. [DOI] [PubMed] [Google Scholar]
- 31.Burton DR. 2002. Antibodies, viruses and vaccines. Nat Rev Immunol 2:706–713. doi: 10.1038/nri891. [DOI] [PubMed] [Google Scholar]
- 32.Ogawa T, Kitagawa M, Hirokawa K. 2000. Age-related changes of human bone marrow: a histometric estimation of proliferative cells, apoptotic cells, T cells, B cells and macrophages. Mech Ageing Dev 117:57–68. doi: 10.1016/S0047-6374(00)00137-8. [DOI] [PubMed] [Google Scholar]
- 33.Takahashi I, Ohmoto E, Aoyama S, Takizawa M, Oda Y, Nonaka K, Nakada H, Yorimitsu S, Kimura I. 1985. Monocyte chemiluminescence and macrophage precursors in the aged. Acta Med Okayama 39:447–451. [DOI] [PubMed] [Google Scholar]
- 34.Wang C, Udupa K, Xiao H, Lipschitz D. 1995. Effect of age on marrow macrophage number and function. Aging (Milano) 7:379–384. [DOI] [PubMed] [Google Scholar]
- 35.Darwich L, Coma G, Bellido R, Ester J, Este A, Blanco J, Borras E, Clotet B, Ruiz L, Rosell A, Parkhouse RME, Bofill M. 2009. Secretion of interferon-gamma by human macrophages demonstrated at the single-cell level after costimulation with interleukin (IL)-12 plus IL-18. Immunology 126:386–393. doi: 10.1111/j.1365-2567.2008.02905.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hernandez-Vargas EA, Wilk E, Canini L, Toapanta FR, Binder SC, Uvarovskii A, Ross TM, Guzmán CA, Perelson AS, Meyer-Hermann M. 2014. Effects of aging on influenza virus infection dynamics. J Virol 88:4123–4131. doi: 10.1128/JVI.03644-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dunnett CW. 1955. A multiple comparison procedure for comparing several treatments with a control. J Am Stat Assoc 50:1096–1121. doi: 10.1080/01621459.1955.10501294. [DOI] [Google Scholar]
- 38.Tecchio C, Micheletti A, Cassatella MA. 2014. Neutrophil-derived cytokines: facts beyond expression. Front Immunol 5:508. doi: 10.3389/fimmu.2014.00508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Parameswaran N, Patial S. 2010. Tumor necrosis factor-α signaling in macrophages. Crit Rev Eukaryot Gene Expr 20:87–103. doi: 10.1615/CritRevEukarGeneExpr.v20.i2.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Schakel K, Kannagi R, Kniep B, Goto Y, Mitsuoka C, Zwirner J, Soruri A, von Kietzell M, Rieber E. 2002. 6-Sulfo LacNAc, a novel carbohydrate modification of PSGL-1, defines an inflammatory type of human dendritic cells. Immunity 17:289–301. doi: 10.1016/S1074-7613(02)00393-X. [DOI] [PubMed] [Google Scholar]
- 41.Stadnyk AW. 1994. Cytokine production by epithelial cells. FASEB J 8:1041–1047. [DOI] [PubMed] [Google Scholar]
- 42.Atias N, Gershenzon M, Labazin K, Sharan R. 2014. Experimental design schemes for learning Boolean network models. Bioinformatics 30:i445–i452. doi: 10.1093/bioinformatics/btu451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Grossmann IE, Biegler LT. 2004. Part II. Future perspective on optimization. Comput Chem Eng 28:1193–1218. doi: 10.1016/j.compchemeng.2003.11.006. [DOI] [Google Scholar]
- 44.Hart WE, Laird C, Watson J-P, Woodruff DL. 2012. Pyomo—optimization modeling in python. Springer International Publishing, Cham, Switzerland. [Google Scholar]
- 45.Hart WE, Watson J-P, Woodruff DL. 2011. Pyomo: modeling and solving mathematical programs in python. Math Program Comput 3:219–260. doi: 10.1007/s12532-011-0026-8. [DOI] [Google Scholar]
- 46.Dietterich TG. 2000. Ensemble methods in machine learning, p 1–15. In MCS Proceedings of the First International Workshop on Multiple Classifier Systems. Springer, Berlin, Germany. [Google Scholar]
- 47.Hoeting JA, Madigan D, Raftery AE, Volinsky CT. 1999. Bayesian model averaging: a tutorial. Stat Sci 14:382–401. doi: 10.1214/ss/1009212519. [DOI] [Google Scholar]
- 48.Domingos P. 2000. Bayesian averaging and the overfitting problem, p 223–230. In ICML Proceedings of the Seventeenth International Conference on Machine Learning (ICML-2000) Morgan Kaufmann Publishers, San Francisco, CA. [Google Scholar]
- 49.Langmead CJ, Jha SK. 2009. Symbolic approaches for finding control strategies in Boolean networks. J Bioinform Comput Biol 7:323–338. doi: 10.1142/S0219720009004084. [DOI] [PubMed] [Google Scholar]