FIGURE 1:

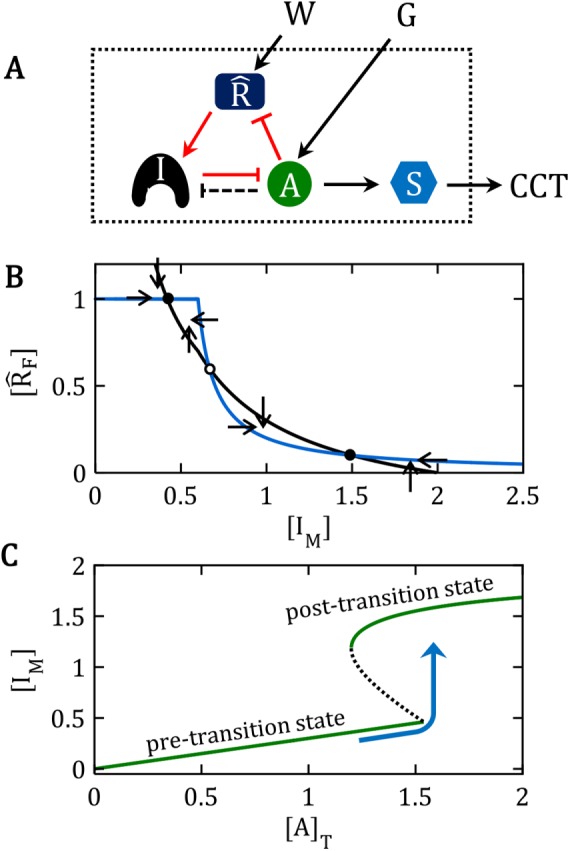
A generic network motif for the bistable switches discussed in this paper. (A) Influence diagram. In an “influence diagram,” barbed arrows (e.g., A → S) mean that “substance A activates substance S,” whereas blunt connectors (e.g., I ⊣ A) mean that “I inhibits A,” without any implications about the molecular mechanism of activation or inhibition. Such influence diagrams are often called “network motifs” because they indicate the “topology” of network interactions without specifying the biochemical mechanism. In this particular influence diagram, A activates S, which promotes a cell-cycle transition (CCT). The CCT is held off by I, which inhibits A. I, A, and 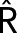are locked in a positive-feedback amplification loop (the red interactions), which is responsible for the bistable switching properties of the motif. The double-negative feedback loop between A and I is responsible for the nonlinear activation of A by a mechanism of “stoichiometric inhibitor ultrasensitivity,” as will be described later. The double-negative feedback loop by itself is not capable of generating bistability, which we indicate by using a dashed connector from A to I (A – – –| I). By activating 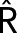, the “wait” signal (W) holds off the CCT and by driving the production of A, the “go” signal (G) promotes the CCT. The motif as a whole is a “signal processing” system (enclosed in the dotted box), which receives “wait” and “go” signals and determines whether the cell will pass the next cell-cycle transition (a binary decision). (B) Phase plane for the network motif in A. In Supplemental Text S1, we propose a simple mathematical model for the influence diagram in A. In the model, the inhibitor I has three forms: I_free, I_modified, and A:I complex, with [I_free] + [I_modified] + [A:I] = [I]_total = constant. Similarly, [A_F] + [A:I] = [A]_T = constant and [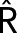_F] + [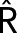_M] = [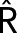]_T = constant, where we have introduced the abbreviations F for “free,” M for “modified,” and T for “total.” The mathematical model is described by a pair of ordinary differential equations for d[I_M]/dt and d[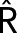_F]/dt. In the “phase plane” (the Cartesian coordinate system spanned by [I_M] and [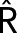_F]), we plot the curves (called “nullclines”), where d[I_M]/dt = 0 (black curve) and where d[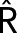_F]/dt = 0 (blue curve), for a particular choice of parameter values (see Supplemental Text S1). The small arrows indicate the directions of the vector field along the nullclines. The nullclines intersect in three places (steady states): two stable steady states (•) separated by an unstable steady state (⚬). (C) Signal–response curve. In the simple mathematical model underlying the phase plane in B, the go-signal is the total concentration of A, and the response variable is the steady-state concentration of I_M (thinking of I_M as representative of all the substrates modified by A). In this diagram, solid green lines represent stable steady states of the bistable switch, and the black dashed line is the locus of unstable steady states. When the signal is small, 0 < [A]_T < 1.5, the concentration of free activator is very small, [A_F] ≈ 0, and substrates of the activator are sparsely modified (e.g., [I_M]/[I]_T < 0.25 in this figure). Hence, the lower branch of green curves represents the pretransition state. When the signal is large, [A]_T > 1.2, the concentration of free activator is large, [A_F] ≈ [A]_T, and substrates of the activator are heavily modified (e.g., [I_M]/[I]_T > 0.75), which represents the posttransition state. The system is “bistable” for 1.2 < [A]_T < 1.5. As [A]_T (the go-signal) increases from 0 toward a final value of 2 (blue curve), the system makes an abrupt transition from the pretransition state to the posttransition state at [A]_T ≈ 1.5. See Supplemental Text S1 for details of this calculation.