Small Airway Absorption and Microdosimetry of Inhaled Corticosteroid Particles after Deposition

Abstract

Purpose

To predict the cellular-level epithelial absorbed dose from deposited inhaled corticosteroid (ICS) particles in a model of an expanding and contracting small airway segment for different particle forms.

Methods

A computational fluid dynamics (CFD)-based model of drug dissolution, absorption and clearance occurring in the surface liquid of a representative small airway generation (G13) was developed and used to evaluate epithelial dose for the same deposited drug mass of conventional microparticles, nanoaggregates and a true nanoaerosol. The ICS medications considered were budesonide (BD) and fluticasone propionate (FP). Within G13, total epithelial absorption efficiency (AE) and dose uniformity (microdosimetry) were evaluated.

Results

Conventional microparticles resulted in very poor AE of FP (0.37%) and highly nonuniform epithelial absorption, such that <5% of cells received drug. Nanoaggregates improved AE of FP by a factor of 57-fold and improved dose delivery to reach approximately 40% of epithelial cells. True nanoaerosol resulted in near 100% AE for both drugs and uniform drug delivery to all cells.

Conclusions

Current ICS therapies are absorbed by respiratory epithelial cells in a highly nonuniform manner that may partially explain poor clinical performance in the small airways. Both nanoaggregates and nanoaerosols can significantly improve ICS absorption efficiency and uniformity.

INTRODUCTION

Inhaled corticosteroid (ICS) therapy is a mainstay in the treatment of multiple respiratory diseases, including asthma (1, 2). When used as a controller medication in asthma, ICS therapy effectively improves airway hyperresponsiveness, symptom control, and quality of life for a large number of patients including children and adults (2–4). Still, current asthma therapy is known to be incomplete and ineffective in a number of areas (3, 5–7). As an inflammatory disease, long-term remodeling of the airways occurs even in children and in cases of well controlled asthma, is not effectively treated with ICS therapy, and leads to a gradual decline in lung function (8). Patients with neutrophilic asthma respond poorly to ICS therapy, but may still require ICS to treat multiple pathways of inflammation (3). Of diagnosed asthma cases, 78% are reported less than totally controlled (9), which results in a US patient group size of approximately 20 million people (10). Refractory asthma, which does not respond to ICS therapy and requires oral steroids with associated significant systemic side effects, occurs in approximately 5% of asthma suffers or 1.3 million people in the US. Recently, Usmani et al. (11) reported that 50–60% of all asthma cases have associated small airway disease, consisting of small airway inflammation, hyperreactivity and dysfunction, which does not typically register on standard lung function tests. Small airway disease severity is strongly linked with asthma symptoms (11).

With current ICS asthma therapies, the small airways are widely considered to be undertreated. The small airways can be classified as having an internal diameter < 2 mm, do not contain cartilage, and generally start with the 8th airway generation together with the alveolar region (7, 12). The small tracheobronchial (TB) airways can be considered to start at approximately bifurcation B8 and continue through the terminal bronchioles at approximately B15, which then lead to the alveolar airways (13). The pathophysiology of asthma includes an increase in airway smooth muscle mass, mucus plugging, and goblet cell hyperplasia in both large and small airways (7). Airflow resistance in the small airways, which is a function of inflammation and luminal narrowing, has been shown to directly correlate with airway hyperresponsiveness (14). Considering an airway structure-function relationship, Tgavalekos et al. (15) demonstrated that significant closure of the small airways was required to match in vivo imaging of ventilation defects in asthmatic subjects. Studies such as Manoharan et al. (16) have shown correlations between small airway disease metrics and asthma symptoms as well as asthma control. Considering refractory asthma, Berry et al. (17) demonstrated that a marker for small airway inflammation (alveolar nitric oxide; NO) was elevated, did not respond to doubling of ICS dose, but was reduced significantly with the oral steroid prednisolone. These results (17) imply that refractory asthma, in many cases, may be the result of small airway dysfunction and an insufficient ICS dose delivered to the small airways with current inhalation therapy. For a wide spectrum of asthma severity, Gelb et al. (18) reported elevated alveolar nitric oxide (consistent with small airway inflammation) in patients receiving ICS, which was reduced with oral steroids. It was therefore concluded that in a patient population of varying asthma severity treated with ICS therapy, the small airways are significantly undertreated and could benefit from improved targeting of ICS delivery.

It has widely been reported that increasing small airway dose of ICS in asthma reduces hyperresponsiveness and improves both symptom control and quality of life (12, 19–22). Furthermore, ICS therapies are topical medications acting on the surface of the lungs, and response is proportional to dose per surface area until the dose-response curve plateaus. However, dose or dose/area values in the small airways have typically not been available due to limitations with in vivo deposition and imaging studies. Recent advances in complete-airway simulations of pharmaceutical aerosol deposition in the lungs have enabled predictions of inhaled medication dose in the small airways (23–28). In these simulations, computational fluid dynamics (CFD) is used to resolve the three-dimensional (3D) time-dependent flow physics of the complex pharmaceutical aerosol delivery process from the site of aerosol formation to the point of deposition (29). For commercially available metered dose inhaler (MDI) and dry powder inhaler (DPI) products, the initial deposition fraction (DF) in the entire tracheobronchial small airway region consisting of bifurcations B8-B15 (bronchioles; Figure 1) is approximately 1%, which for an aerosolized dose of 250 μg of fluticasone propionate (Flovent HFA MDI, GlaxoSmithKline, Raleigh, NC) represents a deposited dose <2.5 μg in this very large lung area (24). Walenga and Longest (13) used a complete-airway CFD model with and without asthma constriction and extended small airway dose to include dose per lung surface area. For the commercial Flovent HFA MDI delivering 250 μg of fluticasone propionate, the surface dose in the region of B8-B15 was 1.3 ng/cm². Using a <2 mm airway diameter criterion to define the small TB region, the deposition fraction was ~0.3% of the aerosolized initial dose. To our knowledge, the cellular efficacy of a surface dose on the order of 1.3 ng/cm² has not been assessed in a controlled in vitro experiment. Therefore, it is not clear if this dose can effectively treat the small TB airways.

Figure 1.

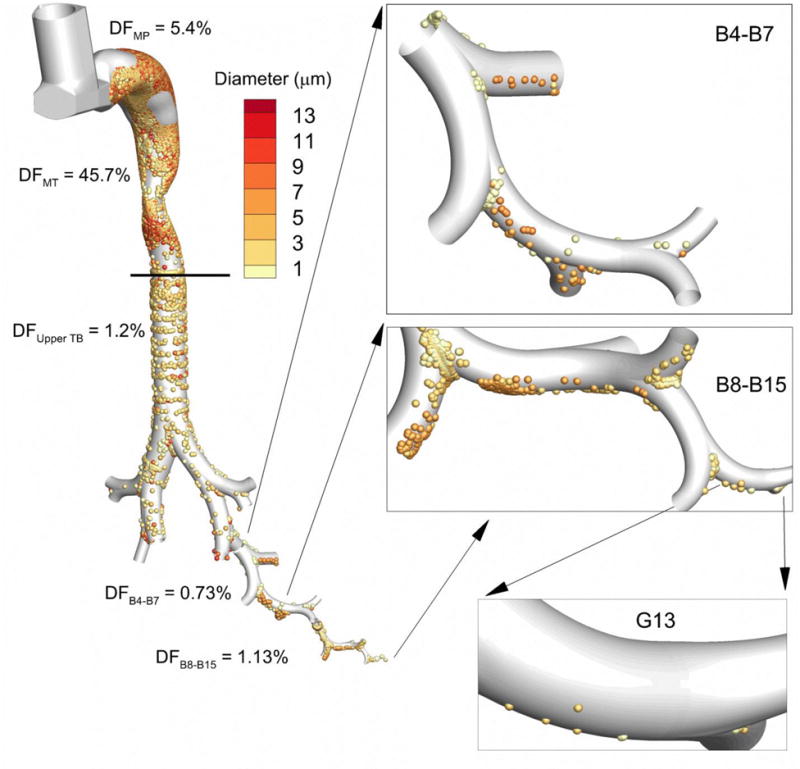
Deposition fraction (DF) from Walenga et al. (13) for the Flovent HFA MDI in the device mouthpiece (MP) and different regions of the conducting airways including the mouth-throat (MT), upper tracheobronchial (TB) region containing the main bifurcation (B1) through B3, and bifurcation segments B4-B7 and B8-B15. Magnified views of deposited particles in the lower airways are shown in the panels, including the deposition of particles in the size range of 1–3 μm in airway generation G13. For an aerosolized dose of 250 μg of fluticasone propionate, Walenga et al. (13) predicted a deposited surface dose in B8-B15 of 1.3 ng/cm², which includes airway generation G13.

As a surface-active medication, the absorption of ICS into the respiratory epithelium is required for efficacy (30). A variety of mathematical models are available to characterize the dissolution and absorption of particles in a solution (31–33). However, these models are typically fit to dissolution data in large volumes of liquid, neglecting the unique thin liquid layer and lipophilic wall arrangement of the airways, and do not include a clearance mechanism. As reviewed by Sakagami (34), a variety of in vivo, in vitro, and ex vivo models are available to assess the pulmonary absorption of ICS and other inhaled pharmaceuticals. Of these models, in vitro tissue-culture air-liquid interface (ALI) experiments provide the most detailed information about the dissolution and absorption process of ICS. Using a realistic aerosol deposition technique, Arora et al. (35) demonstrated that the absorption process of ICS was limited by the amount of fluid in the lungs available for dissolution, resulting in a dissolution limited process. Bur et al. (36) demonstrated the use of a tissue-culture ALI system to evaluate the dissolution and absorption of hydrophilic and lipophilic drug molecules and highlighted the importance of particle size, liquid volume, and realistic aerosol deposition techniques. Other in vitro systems have demonstrated the effect of surfactants on dissolution (37) and the effect of particle physico-chemical form on epithelial uptake (38). Blume and Davis (39) reviewed in vitro and ex vivo cell models of asthma including co-culture models that contain epithelial and immune response cells. While these models are useful, in vitro absorption and asthma models typically do not employ realistic doses of drug concentration consistent with the small airways. Moreover, these in vitro models typically lack a clearance mechanism, geometric realism and wall motion, such that interactions of dissolution, absorption and clearance cannot be assessed.

Based on the need to better understand epithelial absorption of inhaled medications, Rygg, Hindle and Longest (40–42) recently developed a dissolution, absorption and clearance (DAC) computational fluid dynamics (CFD) model of deposited ICS particles in the nasal cavity that resolved 3D transport in the airway surface liquid (ASL) over time. Advantages of this CFD model were the inclusion of clearance together with spatially heterogeneous particle and dissolved drug concentration profiles. The study of Rygg and Longest (42) developed the nasal DAC model and validated results with in vivo nasal clearance (43) and in vitro ICS dissolution(35) data. Rygg et al. (40) evaluated the effect of ICS microparticle size in the range of 1–5 μm on nasal epithelial uptake. Surprisingly, very heterogeneous patterns of nasal epithelial uptake were identified that were influenced by the size of the ICS particles leading to the conclusion that ICS sprays treat the nasal surface in a very nonuniform manner. Previous studies of aerosol deposition have proposed the term microdosimetry (or similar terminology) to characterize these heterogeneous patterns of aerosol deposition (44–49), gas absorption (50–54), and now absorption of dissolved drug into the respiratory epithelium. Microdosimetry can be viewed as the dose received by a small area or even a group of cells relative to a larger region or the entire airway. Finally, Rygg et al. (41) linked CFD absorption predictions to blood concentration values using a pharmacokinetics model and found good agreement with in vivo data (55) for a commercial nasal spray product.

A CFD-based approach similar to the nasal-DAC model can be applied to answer a number of critical questions related to ICS behavior in the small airways and the potential for under treatment as well as improving drug delivery. For example, does absorption of deposited ICS have a chance to occur in the limited fluid volume of a small airway segment before clearance removes the particles? How is the dose of a surface-active ICS distributed within a small airway segment (i.e., microdosimetry)? Particle deposition by sedimentation and the associated microdosimetry and rapid cellular uptake of ICS may result in treating only the lower half (as defined by gravity) of the more distal small airways. Can dissolution be improved with nanoaggregates (56, 57) before clearance occurs? If a true nanoaerosol (50 nm particles) could be delivered, what would be the effect on dissolution of poorly soluble ICS particles and on the microdosimetry pattern? These questions arise from a significant concern with conventional therapy with microparticles (in addition to the low delivered dose) in which sedimentation combined with rapid uptake may only treat an expected 50% of the cells in a small airway segment. The extent that this limited treatment occurs and whether it can be improved with different particle forms is currently not known.

The objective of this study is to predict the cellular-level epithelial absorbed dose from deposited ICS particles in a model of an expanding and contracting small airway segment for different particle forms. Surface dose in the small airway segment is based on the previous complete-airway CFD study of Walenga et al. (13) for a commercial MDI product. The single small airway segment represents generation G13 with a luminal diameter of 0.7 mm. The new small-airway-DAC model simulates transport within the ASL of ICS particles as they dissolve, are absorbed or are cleared by mucociliary motion. Time-resolved simulations are conducted that include breathing motion of the airways for time periods up to 1200 s. Two ICS drugs are considered, which represent different aqueous solubilities. Particle forms considered include typical microparticles from conventional inhalers, nanoaggregates, and true nanoaerosols. Results are intended to highlight both the absorption of these common ICS medications in a highly realistic system as well as the microdosimetry, both of which may render current delivery practices ineffective.

MATERIALS AND METHODS

Airway Selection and Model

For the prediction of ICS dissolution and cellular-level absorption, a single representative airway segment is needed. As shown in Figure 1, the conducting airways are a combination of bifurcations B1-B3, which begin with the trachea and end with the lobar bronchi; B4-B7, which include the remaining bronchi; and B8-B15, which are classified as the bronchioles ending with the terminal bronchioles. Respiratory segments may also be referred to as generations, which exclude the bifurcation component, and begin with the trachea as generation G0. The small airways are generally considered to have a diameter <2 mm and are considered to begin at G8 and below. Within this region, representative generation G13 provides a characteristic model of a small TB airway segment, which feeds the terminal bronchioles. For this first of a kind analysis, the bifurcation structure was expected to add unnecessary complexity, but will be of interest in future DAC studies. The representative airway considered in this study is then generation G13, which has dimensions based on the adult airway model suggested by Finlay (58), with a diameter and length of 0.7 mm and 2.8 mm, respectively, at a resting (end exhalation) lung state.

As shown in Figure 2, the respiratory epithelium in the region of G13 is composed of cuboidal ciliated and nonciliated cells; the nonciliated cells are secretory Clara cells and occur in a higher percentage progressing toward the terminal bronchioles (59, 60). These Clara cells do not produce mucins, resulting in a watery ASL covering of the epithelium in the small airways and little to no mucus in the region of G13 (59, 60). The cilia have a microvillus shape in the lower TB region but maintain action to drive ASL clearance up and out of the lungs (59, 60). The respiratory epithelial cuboidal cells in the region of G13 have a characteristic dimension of approximately 4 μm (60). As shown in Figure 2, the computational 3D mesh (hexahedral shape with straight lines) contains the ASL and borders the respiratory epithelial cells. At the mesh and epithelial cell interface, each mesh control volume face contains a matrix of 4×4 cells. Therefore, the surface dimension of the control volumes is 16 μm and each surface-bound control volume face contains 16 respiratory epithelial cells.

Figure 2.

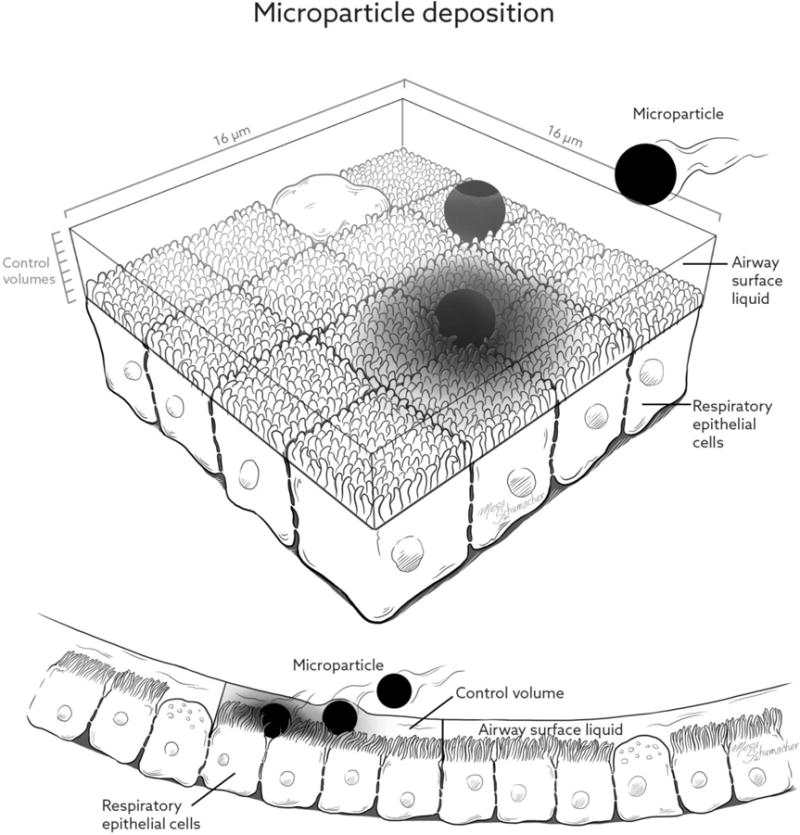
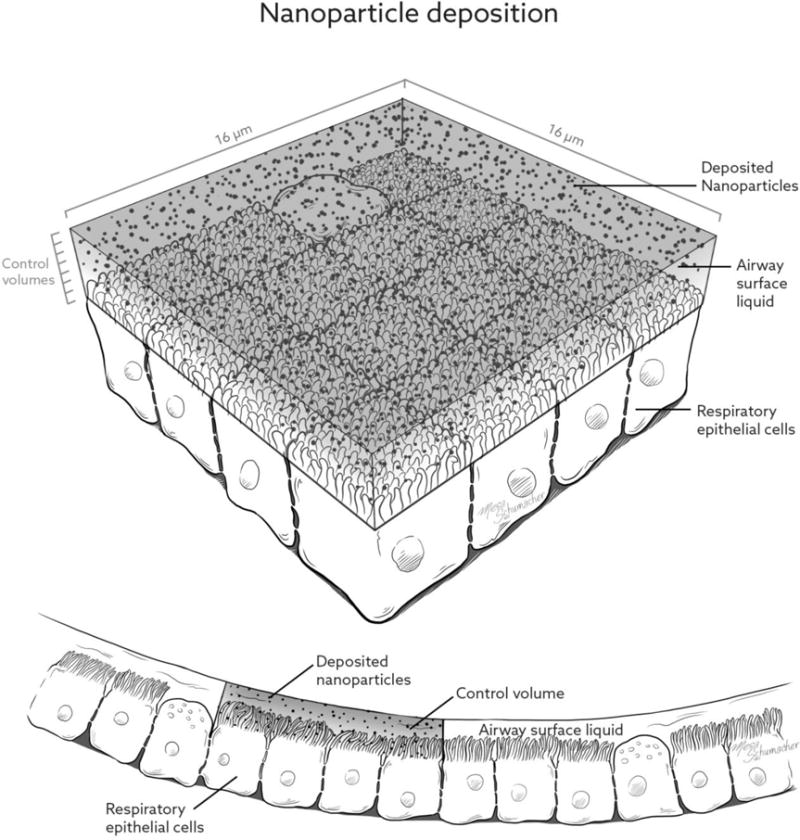
Illustration of the small airway epithelial surface including the airway surface liquid (ASL) and characteristic deposited particles in the form of (a) microparticles and (b) nanoparticles.

The thickness of the ASL is known to decrease from the start of the bronchioles (B8) to the terminal bronchioles (B15) (60). However, without adequate knowledge of this transition, a representative ASL for the entire bronchiolar region was selected based on ICRP (60). The ICRP model estimates the periciliary layer (containing the cilia) to be 4–5 μm thick and the apical fluid above the cilia to be approximately 2 μm. Therefore, the entire ASL thickness in G13 of the model was assumed to be 7 μm, which decreases due to mass conservation as the geometry expands during breathing. Due to a lack of a true mucus layer in G13, constant fluid properties of water were used throughout the ASL, consistent with the observations of Wanner et al. (59). Knowles and Boucher (61) have observed that the cross-sectional ASL flow profile, arising from beating cilia, is that of a half parabola (2nd order function) in a fixed-wall system. This same cross-sectional profile shape was implemented in the current study by assuming zero slip velocity on the cell surface and zero shear stress at the air-liquid interface.

Airway Wall Motion and Clearance

To capture enhanced convection and diffusion associated with wall motion, rhythmic expansion and contraction of the airway model associated with breathing was considered. Respiration conditions were consistent with passive breathing and included a tidal volume of 500 ml, frequency of 12 breaths/min, inspiratory time of 2.5 s, and end-expiratory total lung volume of 3 L. The tracheal flow rate and total lung volume over time for these conditions are shown in Figure 3. The volume change of the lungs was converted to a linear scaling of the geometry, as described by our previous study (26). This linear scaling of the lung geometry was applied to the outer wall of the airway model (epithelial surface). At maximum lung volume, the linear scaling factor was 1.053. It was assumed that ASL mass was conserved over the inhalation and exhalation cycle. Therefore, the ASL layer grew thinner during inhalation (wall expansion) and thicker during exhalation (wall contraction). This ASL mass conservation was enforced using a second scaling factor applied to the inner (air-liquid) surface of the airway model. It was not necessary to simulate the air phase to capture the dissolution, absorption and clearance process. Cross-sectional views of the initially 7 μm thick ASL layer are shown in Figure 3b at minimum (t=0) and maximum (t=2.5 s) extents. Maximum displacement of the ASL surfaces is shown in Figure 3c.

Figure 3.

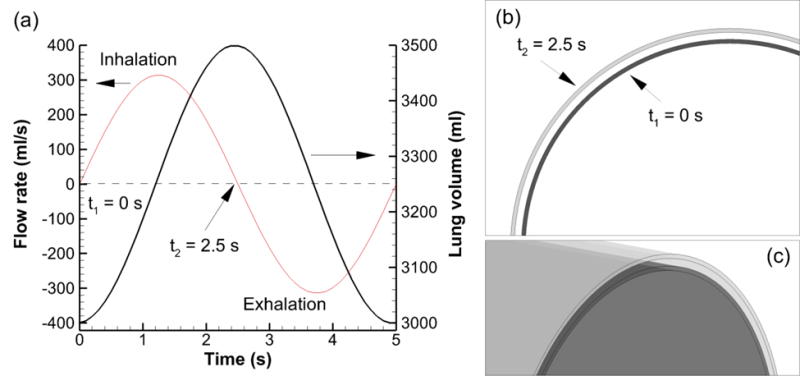
Transient inhalation characteristics for a tidal volume of 500 ml and breathing frequency of 12 breaths per minute expressed as (a) flow rate and lung volume over time, (b) minimum (t = 0) and maximum (t = 2.5 s) expansion of the G13 cross section, and (c) minimum and maximum expansion of the G13 surface model.

Mucociliary clearance is the process by which the ASL layer moves up the respiratory tree due primarily to ciliary action. Clearance velocities in the human small airways are currently not known due to difficulties with conducting controlled experiments. Furthermore, two different theories exist regarding the transition of velocity and mass from the tremendous surface area of the bronchioles to the small surface area of the trachea (59, 61, 62). In one theory, significant fluid resorption occurs as ASL moves up the airway tree to better unify clearance velocity; and in a second theory no resorption occurs, but changes in ASL height combined with very low clearance velocities in the deep lung maintain conservation of ASL mass. In the current study, two clearance velocities that represent a range of potential values were selected. A higher end value of 0.4 mm/min in G13 was selected based on in vivo measurements in an excised rodent lung (62). For this value to be reasonable, significant fluid resorption must occur within the airway, which is expected for healthy lungs (61). As a second value, 0.03 mm/min was selected based on the whole-lung one-dimensional mathematical model of Strum and Hofmann (63), which assumed an exponential decrease in ASL height in the bronchiolar region. These clearance velocities were termed fast clearance (0.4 mm/min) and slow clearance (0.03 mm/min) velocities for this study and were applied as ASL inlet conditions in the distal end of the G13 model. For comparison, a third case was also considered in which the ASL did not move and breathing motion was also neglected, which was termed ‘no motion’.

ICS Selection, Airway Dose, and Particle Forms

To evaluate multiple ICS medications, commonly used budesonide (BD) and fluticasone propionate (FP) were selected. These ICS medications represent a range of aqueous solubilities for hydrophobic molecules, with values of 0.2×10⁻⁴ g/cm³ for BD and 0.14×10⁻⁶ g/cm³ for FP. Both medications are extremely lipophilic, entering the endothelial surface as a dissolved chemical species with negligible resistance, and have a density of approximately 1.3 g/cm³.

Considering dose, Walenga and Longest (13) predicted 1.3 ng/cm² in the bronchiolar region for FP delivered from the Flovent HFA MDI. The measured mass median aerodynamic diameter of the aerosol leaving the inhaler was 2.64 μm (24), which is a reasonable size for both sedimentation and impaction in respiratory generation G13. The surface area of the single G13 segment is 0.06158 cm². As shown in Table 1, the mass of one 2.64 μm microparticle is 0.01252 ng. Considering discrete multiples of particle mass, approximately 6 deposited particles in one segment of G13 provides the closest surface dose to the estimate of Walenga and Longest (13), with a value of 1.22 ng/cm². Based on estimates of impaction and sedimentation, deposition in G13 will be predominately by sedimentation, as also shown in Figure 1 (G13 insert). These deposited 6 particles were placed in the lower half of the ASL at random, as shown in Figure 4, with gravity oriented toward the bottom of the figure (negative y-direction). Figure 4 (top panel) also illustrates how these particles migrate from their starting locations (lower panels) in the direction of ASL motion over a period of 400 s with fast clearance. Interestingly, particles remained on a linear path but progressed and retreated during each expansion and contraction relative to the epithelial cell surface. It is expected that with a bifurcating geometry, some swirling trajectories may become evident.

Table 1.

Characteristics of three particle forms delivering the same deposited dose per surface area in G13.

	2.64 μm Microparticles	2.64 μm Nanoaggregates	50 nm Nanoaerosols
Particle density (BD and FP) [g/cm3]	1.3	1.3	1.3
Mass of 1 particle [ng]	0.01252	0.01252 each nanoaggregatea	8.51E-8
Integer number of particles in airway	6	6 nanoaggregatesb 147,121 nanoparticles each	882,726
Number of simulated parcels	6	600	24,000
Number of particles per parcel	1	1471	36.8
Total drug mass deposited in airway [ng]	0.0751	.0751	0.0751
Deposited dose per surface area [ng/cm2]	1.22c	1.22	1.22

Surface area of one G13 airway: 0.06158 cm² Deposited dose based on CFD estimates: 1.3 ng/cm²

^aPacking fractions are not included

^bNanoparticles composing the nanoaggregates have a diameter of 50 nm

^cValue is different from the target of 1.3 ng/cm² due to the need of an integer number of microparticles

Figure 4.

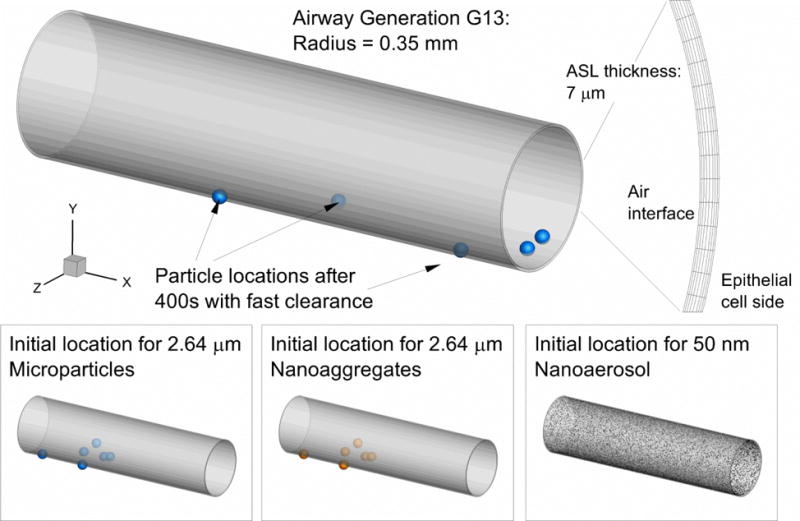
Moving mesh model of the ASL in respiratory generation G13 with a diameter of 0.7 mm. An inlet boundary condition simulated bulk ASL clearance and expanding/contracting wall motion enhanced convective and diffusive transport within the ASL layer.

For comparison with conventional microparticles, both nanoaggregates and nanoaerosols were considered deposited in G13 at an identical total dose (0.0751 ng), which provided an identical total dose/area (1.22 ng/cm²). An identical total dose was assumed for all three particleforms in order to focus on the effects of dissolution, absorption and clearance of different particle forms without the effect of different deposited doses. Nanoaggregates are clusters of nanoparticles that form a microparticle (56, 57, 64, 65). Due to a large aerodynamic size, deposition of nanoaggregates is consistent with microparticles and occurs by impaction and sedimentation. Nanoaggregates are desirable because they are easier to aerosolize than true nanoparticles. Upon deposition in ASL, the nanoaggregate readily dissolves releasing the nanoparticles, which move by Brownian motion within the ASL (66). The increased surface area of the nanoparticles upon release significantly enhances dissolution, which is important for poorly soluble drugs (64). In this study, the nanoaggregate diameter and mass are assumed to be identical to the microparticle case; which neglects a packing fraction. Upon deposition, each of the 6 nanoaggregates releases an equivalent mass of 50 nm nanoparticles, which equates to 147,121 nanoparticles per aggregate (Table 1). The resulting surface dose is again 1.22 ng/cm² to allow for a consistent comparison between cases.

A nanoaerosol consists of nanoparticles in the aerosol state. If a nanoaerosol could be formed at a sufficient concentration for pharmaceutical aerosol drug delivery, the nanoparticles would deposit by Brownian motion instead of impaction and sedimentation. Importantly, the nanoaerosol would therefore more evenly coat the airway geometry (45, 47). As shown in Table 1, the equivalent dose in nanoparticles requires 882,726 discrete 50 nm particles, resulting in a deposited average surface concentration of 1.22 ng/cm². In all three particle delivery forms, the total deposited dose is then 0.0751 ng.

Transport Theory

Motion of the ASL in the moving mesh geometry was defined using the Navier Stokes equations for incompressible transient flow in expanding and contracting control volumes, as presented in Longest and Kleinstreuer (67). The air phase was considered negligible and represented as a zero shear stress boundary condition at the air-liquid interface. The outer and inner surfaces of the ASL were moved at slightly different rates to allow for conservation of ASL mass in the geometry, which required thinning the ASL during inhalation. Additional assumptions included laminar flow based on a very thin ASL height and corresponding small Reynolds number, isothermal conditions, and no effect of gravity on the ASL flow, leading to an axisymmetric ASL layer. Furthermore, the ASL was not allowed to separate and form holes, which is currently debated in the literature, and less likely in the small airways (59). Simplifications of the ASL system included the assumption of water properties to represent thin and watery airway secretions in the small airways (59) and the absence of mucins and cilia. ASL was instead propelled in bulk by the specification of a velocity boundary condition at the distal end of the airway geometry, and largely influenced by the expanding and contracting epithelial wall.

Considering particle transport, initial locations in the ASL were determined at random in the region of expected deposition, as shown in Figure 4. Depth of initial particle location within the ASL was also determined randomly with a uniform distribution. Lagrangian tracking was then employed to determine the trajectory of the dissolving micro and nanoparticles, as described previously for particles in air (68) and liquid (69). For microparticles, forces included in the equation for particle motion were drag, based on the expression of Morsi and Alexander (70), and gravity including the buoyant force. The effect of an applied gravity field on particle motion was neglected in most cases considered, but added in a final case to determine its influence.

Brownian motion was an important consideration and included for the nanoparticle simulations. The random particle motions induced by Brownian motion, governing equations, and implementation have previously been presented by Longest and Xi (71). To accurately capture Brownian motion, the maximum particle time step was on the order of 1×10⁻⁵ s, which created a challenge for simulating dissolution and transport over long periods of time (e.g., 1200 s). Furthermore, it is expected that Brownian motion is enhanced through the expansion and contraction of the geometry, which creates relative motion between circumferential layers of ASL fluid.

Once dissolved, each ICS chemical species (i) was governed by the advection-diffusion equation for species transport, i.e.,

$$\frac{\partial }{\partial t}(\rho Y_i)+\nabla \cdot (\rho \stackrel{\rightharpoonup }{v}{Y}_i)=\nabla \cdot (\rho D_{i,m}\nabla Y_i)+S_i$$ (1)

where ρ is the fluid mixture density, Y_i is the mass fraction of species i, $\stackrel{\rightharpoonup }{v}$ is the fluid velocity, D_i,m is the mass diffusion coefficient of the drug, taken to be 4.3×10⁻⁶ cm²/s (42), and the source term S_i accounts for the addition of drug into the bulk phase from the dissolving particles.

The mass flux (g/cm²-s) of dissolving particles contributing to the source term in Eq. (1) is based on a uniformly dissolving spherical particle and represented as (72)

$$n_{i,\mathit{surf}}=\frac{\rho Sh{D}_{i,m}}{d_p}\left(Y_{i,\mathit{surf}}-Y_{i,CV}\right)$$ (2)

where d_p is the current geometric diameter of each particle. The mass fraction of dissolved drug on the particle surface, Y_i,surf, is the aqueous solubility of each ICS, and Y_i,CV is the current local ICS concentration in each control volume (CV). To account for both convention and diffusion of dissolved drug from the surface of the particle, the nondimensional Sherwood number (Sh) was included based on the empirically derived expression of Clift et al. (73), i.e.,

$$Sh=1+{\left(1+{\mathrm{Re}}_{p}Sc\right)}^{1/3}max\left[1,{{\mathrm{Re}}_p}^{0.077}\right]$$ (3)

where Re_p and Sc are the nondimensional particle Reynolds number and Schmidt number, respectively. Previous simulations of drug particle dissolution have neglected the convective transport and the Sherwood number; however, motion of the airways due to breathing motivates including these convective effects.

Both ICS molecules are considered to be extremely lipophilic, with octanol/water partition coefficients on the order of 5000 or above (40). As a result, the epithelial surface was assumed to provide no resistance to absorption and the surface boundary condition was Y_i,wall = 0. The resulting mass flux of drug into the wall was then calculated as

$$n_{i,\mathit{wall}}=-\rho D_{i,m}{\frac{\partial Y_i}{\partial n}|}_{\mathit{wall}}$$ (4)

where n in the partial derivative is the normal coordinate pointing into the geometry from the wall.

Numerical Methods

Computational fluid dynamics simulations for evaluating ASL flow and particle transport were run using ANSYS Fluent 15 (ANSYS Inc., Canonsburg, PA) coupled with user-defined functions for drug dissolution and absorption. A transient flow solution was calculated using the SIMPLEC algorithm for pressure-velocity coupling, and all transport equations were discretized to be at least 2nd order accurate in space. The solution was determined to be converged when all residuals decreased by at least three orders of magnitude and did not change with additional iterations. The mesh resolution was found to be sufficient, as increasing the number of computational cells spanning the ASL layer beyond 10 had a negligible effect on the flow solution. Within the ASL flow field, transient simulations of coupled particle transport, dissolution, and species transport were carried out for a total clearance time of 1200 s after initial aerosol deposition. Additional stopping conditions were full dissolution of all particles or <0.5% of initial mass remaining for nanoaggregates. At each time step, a sufficient number of iterations were performed to converge the solution of all transport equation. The ASL solution time step of 0.1 s was selected as the mean diffusion time for the solute to spread over the 16×16 μm CV. That is, mean diffusion distance in three dimensions

$$\langle x\rangle =\sqrt{6Dt}$$ (5)

where D = 4.3×10⁻⁶ cm²/s and t = 0.1 s, is 〈x〉 = 16 μm.

By selecting a coupled grid-size and fluid-flow time step in this manner, both time step and grid independence were achieved.

As described in previous studies (74), it is not always possible to simulate all physical particle trajectories in a two-way coupled simulation. Instead, representative particles or ‘parcels’ are considered to capture a specific number of physical particles. In this manner, the correct mass of the delivered medication can be achieved, together with the correct two-way coupling, while maintaining computational efficiency. As shown in Table 1, parcel approximations were used to represent the very high number of nanoparticles. It was determined that 24,000 nanoparticle parcels were required to resolve the wall absorption of the over 880,000 nanoparticles in the physical system, resulting in approximately 37 nanoparticles per parcel. Because the nanoaggregates were deposited in a more confined area of G13, absorption could be accurately resolved with 600 nanoparticle parcels (Table 1).

Model Validations

A critical challenge for the CFD model is to correctly predict the dissolution rate of particles at a high concentration (well beyond the solubility limit) in a limited volume of fluid. The previous study of Arora et al. (35) evaluated the dissolution of multiple ICS types deposited on an air-liquid interface in an in vitro Transwell system with limited fluid. In the previous study of Rygg and Longest (42), we implemented the dissolution model and assumptions employed in the current study and compared the CFD predictions of ICS dissolution and transport with Arora et al. (35). For a three order of magnitude difference in ICS solubilities, predictions of drug dissolution and transport through the Transwell membrane were within approximately 5% relative difference of the experimental results over a time period of 1.5 hours. The dissolution curves were nonlinear due to high concentrations, and illustrated an initial burst effected, which was very small considering the limited volume of fluid and very low solubility values. Additional relevant validations of DAC simulations in the small airways are difficult due to a current lack of experimental data and associated experimental complexities, as described in the Discussion.

Absorption Metrics

The focus of this study is absorption of ICS into respiratory epithelial cells. As with previous aerosol deposition studies, absorption can be defined in terms of an absorption fraction and absorption efficiency. An absorption fraction (AF) is defined as

$$A{F}_i=\frac{\mathit{mass}of\mathit{cellular}\mathit{absorption}in\mathit{region}i}{\mathit{initial}\mathit{mass}\mathit{of}\mathit{aerosolized}\mathit{drug}}.$$ (6)

Regions for calculating AF may be broad areas of the respiratory tract, as in Figure 1, or individual airways, as with the current study. An absorption efficiency (AE) is defined as

$$A{E}_i=\frac{\mathit{mass}\mathit{of}\mathit{cellular}\mathit{absorption}\mathit{in}\mathit{region}i}{\mathit{mass}\mathit{of}\mathit{drug}\mathit{deposited}\mathit{in}\mathit{region}i}.$$ (7)

In this study, total epithelial cell absorption within the G13 model, based on the constant amount of mass deposited in G13, will be expressed as an AE.

Of the mass that is absorbed in a region, a measure is needed that can predict how uniformly or nonuniformly (localized) the dose is distributed. As with deposition, an absorption enhancement factor (AEF) is defined as

$$\mathit{AEF}=\frac{\raisebox{1ex}{$m_{CV}$}\!\left/ \!\raisebox{-1ex}{$A_{CV}$}\right.}{\raisebox{1ex}{$m_{\mathit{total}}$}\!\left/ \!\raisebox{-1ex}{$A_{\mathit{total}}$}\right.}$$ (8)

In the equation above, m_cv and A_cv are the absorbed mass and surface area, respectively, of the control volume (CV) faces contacting the epithelial surface. As described, each surface CV face contains a 4×4 matrix of 16 epithelial cells. Variables mtotal and Atotal are the absorbed mass and surface area of the total airway generation considered, i.e., G13, resulting in local dose per surface area normalized by the total area-averaged dose. Ideally, the deposited dose is evenly divided over the geometry giving an AEF of 1 in all cells. In contrast, an AEF of 1000 in a single CV indicates that the associated group of 16 cells receives 1000-fold more dose than the total area-averaged dose. An AEF of 0.1 indicates that a group of 16 cells receives only 1/10 the total area-averaged dose. It is also possible for AEF to be zero, indicating no absorbed dose for a local group of cells.

RESULTS

Total Absorption Efficiency in G13

Characteristics of the total absorption efficiency (AE) throughout G13 are presented in Table 2. Considering BD, approximately 100% of the deposited dose was absorbed into the airway wall for the three particle forms and different clearance conditions. Minor exceptions included the case of microparticles and fast clearance, where one BD particle exited before fully dissolving, leading to a total AE of 95.5%. Brownian motion also caused some of the nanoparticles to exit the geometry before complete dissolution could occur, leading to total AE values in the range of 99–100%. While total AE of BD was near 100% in all cases, characteristic time to reach full absorption was significantly different and depended on particle form. The relatively low aqueous solubility of BD resulted in dissolution times for the microparticles on the order of 300 to 350 s. As anticipated, the increased particle surface area of the BD nanoaggregates reduced the dissolution and absorption time by 2 orders of magnitude to approximately 4 s. Due to the very rapid uptake of BD at the epithelial surface, absorption time for the true nanoaerosol was less than 1 s. For BD, slow vs. fast clearance had little impact on the total absorption metrics.

Table 2.

Total wall uptake characteristics including total absorption efficiency (AE), characteristic absorption time, and absorption observations.

	Budesonide (BD)	Fluticasone propionate (FP)
2.64 μm Microparticles - No motion
Total AE (%)	100.0	0.6
Characteristic time (s)	343	1200
Observations	Fully dissolved	Max run time reached
2.64 μm Microparticles - Slow clearance
Total AE (%)	100.0	1.0
Characteristic time (s)	300	1200
Observations	Fully dissolved	Max run time reached
2.64 μm Microparticles - Fast clearance
Total AE (%)	95.5	0.37
Characteristic time (s)	352	674
Observations	One particle exited; others fully dissolved	All particles exited prior to full dissolution
2.64 μm Nanoaggregates - Slow clearance
Total AE (%)	99.8	20.4
Characteristic time (s)	4.3	120
Observations	Fully dissolved	<5% mass remaining in G13
2.64 μm Nanoaggregates - Fast clearance
Total AE (%)	99.3	21.0
Characteristic time (s)	4.0	120
Observations	Fully dissolved	<5% mass remaining in G13
50 nm Nanoaerosol - Fast clearance
Total AE (%)	99.9	89.7
Characteristic time (s)	0–0.2 s	25.9 s
Observations	Fully dissolved	Fully dissolved

Due to the very low aqueous solubility of FP, total AE in G13 for 2.64 μm microparticles was two orders of magnitude (or more) lower than with the same conditions and BD. For FP microparticles with no motion or slow clearance, the maximum run time of 1200 s was reached with ≤ 1% total AE. With fast clearance, all particles exited within approximately 670 s, and total AE was only 0.37%. Nanoaggregates of FP dramatically improved total AE compared with microparticles, with values of approximately 20% for both slow and fast clearance. In both cases, <5% of the aerosol remained in the geometry at 120 s, which was one of the stopping criteria for the simulations. Nanoaerosols of FP further increased total AE by a factor of 4.5, compared with nanoaggregates, reaching approximately 90% absorption after 25.9 s. Compared with microparticles under fast clearance conditions, nanoaerosols increased total absorption by over 2 orders of magnitude (0.37 vs. 89.7 %) and decreased absorption time by a factor of 26-fold (674 vs. 25.9 s).

Cellular Distribution of Absorption

Cellular distributions of absorption are expressed in both tabulated (Table 3) and graphical (Figures 5 and 6) formats. Table 3 reports the percentage of epithelial cells within the G13 model receiving different percentages (50, 90 and 99%) of the total absorbed dose. For fully uniform distribution, 50, 90 and 99% of total absorbed dose (column headings) should be received by 50, 90 and 99% of epithelial cells (table values). In contrast, lower percentages of absorbing cells imply that the dose is taken up by only a few cells producing a non-uniform dose distribution where some cells receive more than the total area-averaged dose and many cells are untreated. Considering 2.64 μm microparticles of BD and fast clearance, Table 3 indicates that 99% of the absorbed dose is received by only 1.7% of the epithelial cells (Note a - Table 3). This is an example of a highly nonuniform dose distribution as the remaining 98.3% of cells receive the 1% of remaining dose. FP might be expected to improve the dose distribution profile as microparticles dissolve more slowly and therefore interact with more epithelial cells. However, Table 3 indicates that with microparticles of FP, 99% of the dose is received by only 3% of the epithelial cells. Due to relatively rapid dissolution and absorption of BD, nanoaggregates do not improve the highly nonuniform dose distribution profile with, for example, 99% of the dose going to approximately 2% of the cells under fast and slow clearance conditions (Table 3). The slower absorption of FP combined with nanoaggregates begins to improve the uptake distribution. For example, 99% of the FP nanoaggregate dose is absorbed by approximately 40% of the cells; however, approximately half the absorbed dose (50% column) is absorbed by only 5% of the cells. A primary advantage of nanoaerosols over the nanoaggregates is significantly improved distribution of the dose, where with FP 99% of the absorbed dose is received by 92.3% of the cells (Note b). Nanoaerosol absorption characteristics are somewhat better for FP than for BD because the longer dissolution time of FP allows more Brownian motion to occur, which spreads the dose over more cells.

Table 3.

Percentage of epithelial cells (table values) within G13 receiving 50, 90 and 99% of total absorbed dose for each case.

	Budesonide (BD)			Fluticasone propionate (FP)
	50% of dose	90% of dose	99% of dose	50% of dose	90% of dose	99% of dose
2.64 μm Microparticles
No motion (% cells)	0.013	0.022	0.022	0.013	0.03	0.03
Slow clearance (% cells)	0.084	0.43	0.62	0.063	0.26	0.51
Fast clearance (% cells)	0.32	1.3	1.7a	0.77	2.3	3.0
2.64 μm Nanoaggregates
Slow clearance (% cells)	0.40	1.5	2.2	4.4	24.3	41.3
Fast clearance (% cells)	0.44	1.7	2.4	5.0	25.9	43.0
50 nm Nanoaerosol
Fast clearance (% cells)	19.9	53.4	63.1	19.1	67.8	92.3b

In uniform absorption 50% of the dose should be received by 50% of the cells (linear relation).

^aHighly nonuniform absorption with 99% of the absorbed dose received by only 1.7% of the cells.

^bUniform absorption with 99% of absorbed dose received by 92.3% of the cells.

Figure 5.

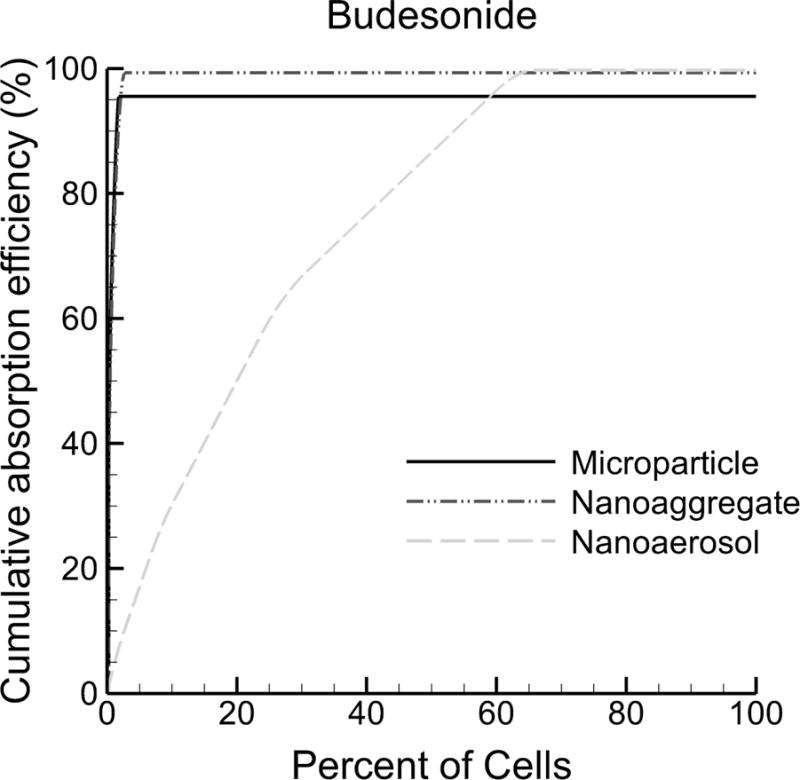
Cumulative absorption efficiency of budesonide (BD) into the respiratory epithelial cells as a percent of initially deposited drug mass for fast clearance conditions. The position where the cumulative absorption curve becomes horizontal denotes a dividing line in each case between the percentage of cells absorbing drug (left of the horizontal position) and percentage of cells not absorbing drug (right of the horizontal position). Both microparticles and nanoaggregates of BD are absorbed by very few cells in the geometry. For example, >95% of the cells receive no drug with the microparticle and nanoaggregate forms. In contrast, the nanoaerosol provides drug to a majority of the epithelial cells (~63%). The maximum cumulative absorption efficiency is equal to the total absorption efficiency (AE) reported in Table 2.

Figure 6.

Cumulative absorption efficiency of fluticasone propionate (FP) into the respiratory epithelial cells as a percent of initially deposited drug mass under fast clearance conditions. With microparticles, >95% of cells receive no drug and total absorption efficiency (AE) is very low (<1%). Nanoaggregates improve AE by a factor of 57-fold and increase the number of cells receiving drug to approximately 43%. The Nanoaerosol treats nearly all cells (~92%) and further increases total absorption to approximately 90%.

The distribution of the cellular dose is presented in Figures 5 and 6 as cumulative absorption efficiency as a function of cellular percentages. Absorption efficiency values on a cellular basis are summed from highest to lowest resulting in a cumulative AE curve. The point where the cumulative curve becomes horizontal denotes the percentage of cells that receive some (e.g., at least 1%) of the total absorbed dose. Cellular percentages beyond this horizontal transition point do not receive an appreciable amount of the total absorbed dose. The cumulative absorption efficiency curves have a maximum value equal to the total AE, as reported in Table 2. Considering BD (Figure 5), microparticles and nanoaggregates are each observed to treat only <5% of cells, leaving >95% of cells untreated, which is consistent with Table 3. In contrast, the nanoaerosol curve results in a more gradual rise to approximately 63%, where the curve becomes horizontal, indicating that approximately 37% of cells are untreated.

With FP (Figure 6), microparticles again treat <5% of all cells. A log scale on the y-axis is used in Figure 6 to capture the dramatic increases in total AE achieved by using nanoaggregates (54-fold increase compared to microparticles) and nanoaerosols (greater than 2 order of magnitude increase compared with microparticles). As with Table 3, nanoaggregates of FP treat approximately 40% of cells leaving approximately 60% untreated. The nanoaerosol increases the fraction of cells receiving some (at least 1%) of the absorbed dose to approximately 90%.

Absorption Enhancement Factors

Contour plots of AEF for BD vs. FP and microparticles, nanoaggregates, and nanoaerosols are shown in Figures 7, 8 and 9, respectively. As described, each 16×16 μm surface square in these figures represents a set of 16 respiratory epithelial cells. Beginning with microparticles, straight line trajectories are observed with cells only directly under the particles absorbing drug (Figure 7). This arrangement is due to the relatively slow dissolution together with fast absorption of the lipophilic dissolved drug into the respiratory epithelial cells. Different penetration depths of the microparticles in the ASL result in different travel distances and higher AEF values arising for slower particles. Cases where AEF is equal to 1000 are shown, consistent with previous observations in this study that a majority of the dose is receive by only a few of the cells. Figure 8 illustrates improvements in dose distribution with nanoaggregates. Brownian motion of the nanoparticles is responsible for the random absorption patterns coupled with persistent clearance motion. The much slower dissolution of FP allows a longer time for Brownian motion to distribute the dose to more cells. Values of AEF below 0.1 are not contoured (i.e., shown as clear), indicating a high fraction of relatively untreated cells (Figure 8). The use of nanoaerosols causes AEF values to approach the ideal case of 1 for a majority of the cells in the geometry (Figure 9). As indicated in Table 3, FP and the nanoaerosol is observed to provide the most uniform distribution of drug concentration of the cases considered in this study.

Figure 7.

Absorption enhancement factor (AEF) for microparticles with fast clearance for (a) BD and (b) FP. Values of AEF below 0.1 are not contoured (i.e., they are clear). AEF represents the local absorption in a 16×16 matrix of surface epithelial cells normalized by the total area-averaged absorption in the small airway geometry. An AEF of 1000 in a single element indicates 1000 times more ICS absorption in a 16×16 matrix of cells compared to the total dose per total area.

Figure 8.

Absorption enhancement factor (AEF) for nanoaggregates with fast clearance for (a) BD and (b) FP. Values of AEF below 0.1 are not contoured.

Figure 9.

Absorption enhancement factor (AEF) for nanoaerosols with fast clearance for (a) BD and (b) FP. Values of AEF below 0.1 are not contoured.

Effects of Gravity

Results presented in previous sections neglected the effect of gravity on particle motion. However, the ICS molecules considered in this study have a density greater than 1 g/cm³, which is expected to cause sedimentation in watery ASL. The amount of sedimentation will vary depending on the amount of mucins and binding proteins in the ASL, which is not known for the small airways. As an extreme case, we neglected the presence of mucins and binding proteins and simulated gravitational settling as it would occur in watery ASL with the gravity vector oriented in the negative y-direction (Figure 4). For 2.64 μm microparticles of BD, sedimentation within the ASL greatly reduces the extent of particle motion (Figure 10a) as the particles collect near the epithelial surface in very low velocity regions. For some particles, reverse motion against the primary direction of clearance is observed. This reverse motion occurs very near the wall and is believed to be the result of complex flows generated during geometry expansion and contraction. In all cases, the microparticles settle toward the lowest point of the geometry. While the trajectories are different, the absorption characteristics are largely unchanged with the inclusion of gravity for microparticles. For BD microparticles and fast clearance, total AE is approximately 100%, as for all BD cases in Table 2 without gravity. The dose distribution is also highly concentrated with gravity where 50, 90 and 99% of the absorbed dose is received by 0.11, 0.28 and 0.39% of the epithelial cells, respectively. For the nanoaerosol case, gravity had a negligible effect on absorption. Specifically, due to the very small size and relatively fast dissolution times, total AE and the dose distribution metrics of nanoaerosols were virtually unchanged by gravity.

Figure 10.

Absorption enhancement factor (AEF) including the effects of gravity and fast clearance for (a) microparticles and (b) nanoaerosol. Values of AEF below 0.1 are not contoured. Initial locations of the microparticles and orientation of the gravity vector are shown.

DISCUSSION

A primary finding of this study is the very limited regional distribution of ICS absorption from conventional microparticles within a small airway generation. It was expected that due to deposition by sedimentation, and the fact that the small airways occupy a vast majority of lung surface area, conventional ICS may only treat the lower half of the lung surface as defined by the direction of the gravity vector. However, using realistic pharmaceutical aerosol delivery conditions, it was predicted that <5% (range 0.62 - 3 %) of the epithelial cells absorbed the majority (99%) of the deposited dose for both ICS medications (Table 3). Based on the cumulative absorption curves for conventional sized microparticles (Figures 5 and 6), >95% of small airway cells absorbed no drug. This observation must also be considered with the predicted very low doses deposited in the small airways, as calculated by Walenga and Longest (13). The predicted deposited dose in the G13 airway segment delivered from a conventional MDI was only 0.0751 ng. For BD, approximately 100% of the deposited dose was absorbed in the G13 model; however, for FP the total absorbed dose was 1% or less, resulting in a maximum absorbed dose of 0.751 pg. Ineffective treatment of small airway disease with conventional ICS therapy therefore appears to have two possible causes. First, very low deposited and absorbed drug masses; and second, the deposited dose is distributed to only a small percentage of cells (<5%) within the airway.

A number of clinical studies have shown that small particle ICS therapies, with aerosol MMAD values of approximately 1 μm, reduce airway hyperresponsiveness and improve asthma symptoms as well as quality of life (5, 7, 12). The small particle ICS products are expected to improve drug mass delivery to the small airways, which is consistent with multiple in vivo (75–79) and recent complete-airway CFD predictions (80, 81). It is widely reported that the improved small airway response to small particle ICS therapy is due to increased dose (5, 12, 82), which is an important factor. However, results of the current study point to additional reasons for this improved clinical response. For poorly soluble medications like FP, it is well known that smaller particles will increase particle surface area for dissolution thereby increasing the amount of drug available for epithelial absorption. As highlighted in this study, an increased number of small particles will cover more airway surface area thereby treating more cells. For example, the mass of drug in 6 particles with a diameter of 2.64 μm is equal to 110 particles with a diameter of 1 μm. As a result, for the same deposited dose, the 1 μm particles should treat 18-fold more cells, assuming similar trajectory lengths before the particles are fully dissolved. Increasing the deposited dose in the small airways is an important contribution of small particles. However, the current study proposes that observed clinical improvements may also be a function of improved microdosimetry and more uniform absorption associated with small particles on the order of 1 μm.

A second primary finding of this study is that nanoaggregates and nanoaerosols can significantly improve dose distribution within a small airway model. Previous studies have proven that nanoaggregates have an improved dissolution profile (31, 56, 57). Results of the current study verify these findings with a 57-fold increase in the total absorption efficiency of FP with nanoaggregates compared with microparticles under fast clearance conditions (Table 2). Perhaps not previously realized is that nanoaggregates can also improve the surface coverage for absorption. For example, nanoaggregates of FP reduced the fraction of untreated cells from >95% with microparticles to approximately 60%. However, for more rapidly dissolved and absorbed BD, nanoaggregates did not significantly improve the absorbed dose uniformity. In contrast with nanoaggregates, true nanoaerosol (50 nm) particles resulted in near 100% absorption of both ICS molecules and a highly uniform absorption profile. For FP delivered as a nanoaerosol, most epithelial cells received an equal fraction of the dose. These quantified advantages of nanoaerosols compared with microparticles and nanoaggregates motivate continued research efforts into this form of pharmaceutical aerosol generation and delivery (83).

A significant assumption of this study was the deposition of the same initial drug mass (dose) in G13 for each of the different particle forms. Nanoaggregates have aerodynamic diameters similar to conventional microparticles resulting in similar deposition mechanisms of impaction and sedimentation. Kuehl et al. (31) report nanoaggregates with diameters in the range of 1–5 μm. Therefore, it is reasonable that a nanoaggregate aerosol delivered at the same initial dose and with a similar aerodynamic diameter would provide a very similar deposited dose profile compared with a conventional microparticle aerosol. In contrast, nanoaerosols in the range of 50 nm deposit primarily by Brownian motion (84), with particle charge also potentially playing a role. Deposition by Brownian motion in an airway becomes directly proportional to residence time and inversely proportional to particle velocity (85–87), which is reversed for microparticles. Airflow velocities are known to decrease with depth into the bifurcating airway tree. Therefore, nanoaerosols provide a technique to potentially increase the deposited dose delivered to the small airways. The focus of this study was to evaluate dissolution, absorption and clearance of different particle forms in the absence of delivered dose differences. Therefore, it was necessary to assume the same initial particle dose for the three aerosols considered. Future studies may consider the combined nanoaerosol effects of increased small airway drug deposition, with properly engineered systems, together with improved dissolution and more uniform drug absorption.

An interesting observation is that clearance and airway wall motion influenced the total absorption in some cases. For nanoaerosols and nanoaggregates, Brownian motion dominated particle transport such that including clearance was not necessary. However, airway expansion and contraction significantly augmented diffusion due to Brownian motion (data not shown). The combination of clearance and airway wall motion had a large impact on the absorption of FP from microparticles. Slow clearance and airway wall motion increased total AE from 0.6 with no motion to 1.0%. Implementing fast clearance then caused the particles to exit the geometry thereby reducing dissolution, resulting in a total AE of 0.37%. As a result, clearance and airway wall motion may influence transport related uptake factors in a manner that has not previously been considered and is currently not included in published in vitro testing methodologies.

It is difficult to compare results of the current simulations with existing ALI cell-culture in vitro experiments. As described in the Methods, we have previously implemented the dissolution and absorption model used in this study to predict in vitro results of ICS particle dissolution in the absence of cells with a limited ASL fluid in a Transwell geometry (42). However, significant differences exist between current dissolution cell experiments, ALI in vitro models, and the small airway model presented in this study. In vitro Transwell systems typically contain a limited amount of basolateral fluid, which is sampled for quantification of transport (36). In contrast, the small airway system of this study assumed that absorbed ICS was carried away by the blood resulting in diffusion into a semi-infinite medium. As described by Bur et al. (36), ALI in vitro systems typically have a large volume ASL (e.g., 0.5 ml) or a reported dry surface. The dry interface has an unknown amount of fluid that is likely proportional to the osmolarity of the deposited drug; otherwise dissolution could not occur. In contrast, the CFD model allows for the definition of a known amount of apical liquid volume and ASL height. Finally, very large doses per area compared to an in vivo perspective are applied to in vitro systems, typically to enable drug quantification (36). These doses result in transport rates that are measured in ng/s over the course of hours. Use of the small-airway-DAC model enabled initial application of a realistic deposited dose per area value with a total initial dose below 0.1 ng consistent with predictions for the small airways. Even at this very small initial dose, absorption was still observed to be limited by the available ASL and low aqueous solubility of ICS medications. Advantages of in vitro ALI systems include physical realism, multiple cellular uptake mechanisms with realistic cellular response, and a controlled scientifically repeatable platform. In comparison, a number of highly relevant factors for small airway uptake can be analyzed with the new CFD-based DAC model including realistic surface doses, effects of clearance and wall motion, accurate specification of ASL height, and microdosimetry predictions.

Gravity was observed to affect trajectories of microparticles, but did not affect nanoaggregates and nanoaerosols. Including gravity represents an extreme case as binding proteins in ASL will tether particles and hold them at an equilibrium position that is controlled by surface contact forces (88). Surprisingly, very near the epithelial surface reverse flow currents caused some of the particles to move in the direction opposite of bulk clearance. However, even in this extreme case, general observations of the study were similar. Total uptake of microparticles and nanoparticles was not altered. Dose distribution of microparticles did become even more nonuniform. Neglecting gravity can therefore be considered a conservative estimate of the degree of dose non-uniformity for microparticles with gravity increasing dose non-uniformity even further.

The small-airway-DAC model provides a consistent platform for assessing the absorption and microdosimetry of different ICS drugs and particle forms. However, a number of limitations are associated with this model. First, only one airway segment without a bifurcating region was assessed in this initial proof-of-concept study. Absorption in the complete lung will be increased as low solubility particles move from one generation to the next by mucociliary clearance. Therefore, total lung AE of FP will be higher than reported within the generation G13 unit alone. However, dose to the small airways will remain limited for low solubility ICS medications as the alveolar region lacks mucociliary clearance such that very few more distal particles will be cleared into G13. Bifurcations are also known to be regions of high particle deposition (45, 47, 89) and frequently reduced mucus clearance (90). The inclusion of cilia and mucins may alter the characteristic of ASL transport and velocity profiles. However, complex secondary flows and mixing were not observed in this very low Reynolds number system. Furthermore, both cilia and mucins are less concentrated in the small airways leading to watery ASL without a defined mucus layer (59). A simple particle dissolution model was employed that does not account for crystallinity, excipients and aerosol source, which may impact dissolution and solubility (38). At much higher doses, concentrations of ICS in blood and tissue may limit absorption, as we have previously predicted for inhaled gases (52, 91). Considering a single particle size is also a limitation, as polydisperse particles in a size range of 1–4 μm would be expected to reach and deposit in the small airways with conventional delivery. However, an approximate MMAD of 2.6 μm was predicted to enter the small airway and alveolar region from a spray inhaler (26), verifying that the current predictions are reasonable.

Conclusions

In conclusion, this study has presented a new small-airway-DAC model for assessing the respiratory epithelial absorption and microdosimetry of ICS medications. Different particle forms were shown to have a significant effect of total absorption efficiency and microdosimetry as a function of ICS solubility. Nanoaggregates of FP were shown to increase total absorption efficiency by a factor of 57-fold and a nanoaerosol further increased absorption efficiency to near 100%. Microdosimetry predictions of conventional microparticles in the small airway model indicated highly nonuniform absorption patterns with <5% of cells receiving drug. Nanoaggregates improved absorbed dose distribution of FP but not for BD. Nanoaerosol particles provided the best microdosimetry profile with near uniform absorption for FP. Based on improved uptake and microdosimetry characteristics, nanoaggregates are expected to provide clear benefits for targeting medications to the small airways, which can be further improved with nanoaerosols. Practical devices for safely delivering pharmaceutical doses of nanoaerosols to the lungs are currently not available. However, results of the current study highlight the potential advantages that could be achieved in terms of cellular-level absorption and microdosimetry characteristics if a practical nanoaerosol device for ICS delivery was developed.

ABBREVIATIONS

1D

one dimensional

3D

three dimensional

AE

absorption efficiency

AEF

absorption enhancement factor

AF

absorption fraction

ALI

air-liquid interface

ASL

airway surface liquid

B#

airway bifurcation number

CFD

computational fluid dynamics

CV

control volume of the computational mesh

DAC

dissolution-absorption-clearance

DPI

dry powder inhaler

FP

fluticasone propionate

G#

airway generation number

HFA

hydrofluoroalkane

ICS

inhaled corticosteroid

MDI

metered dose inhaler

BD

budesonide

NO

nitric oxide

TB

tracheobronchial