Fig. 1.

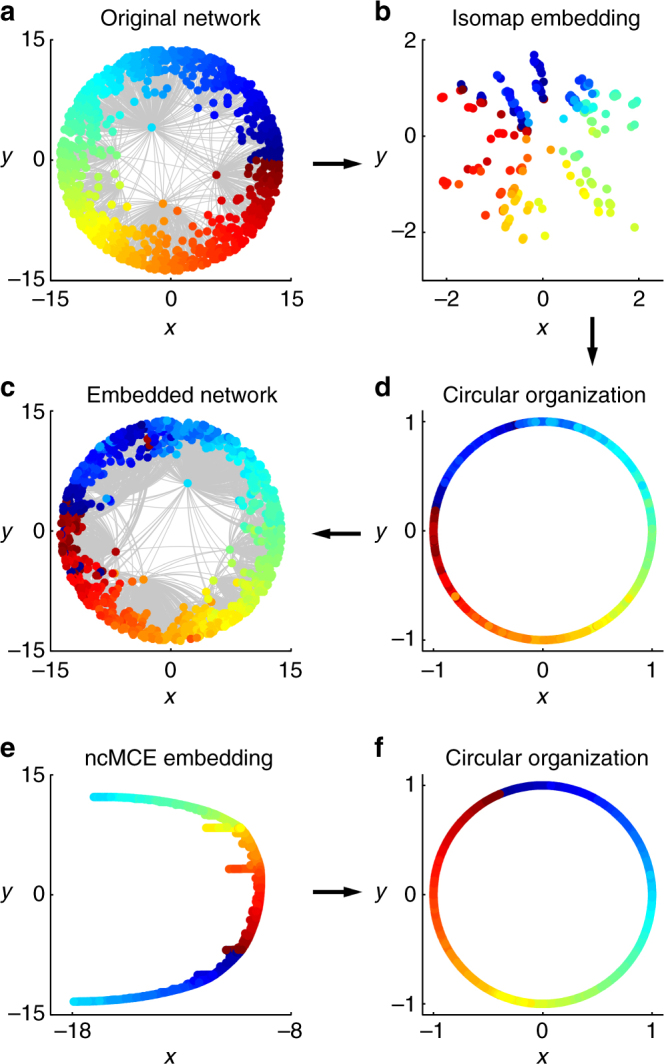
Coalescent embedding. a We show the original synthetic network generated by the PSO model in the hyperbolic space. b The Isomap algorithm (ISO), which is the progenitor of manifold techniques, starting from the unweighted adjacency matrix offers an embedding of the network nodes that is organized according to a circular pattern that follows the angular coordinates of the original PSO model. We made different trials using other synthetic networks, and this circular pattern is mainly preserved if the kernel is centered or if the kernel is not centered and the first dimension is neglected (see “Methods” section for details). This makes sense because the operation of kernel centering puts the origin of the reduced space at the center of the points in a multidimensional space and thus at the center of the manifold. Since the node points lie on the hyperbolic disk, the embedding places the origin approximatively at the center of the disk. d The nodes are projected over a circumference and adjusted equidistantly according to the step 3.2 of the algorithm described in “Methods” section. c The radial coordinates are given according to Eq. (4). e A different pattern is obtained for an algorithm named ncMCE. The circular pattern is linearized and the nodes are ordered along the second dimension of embedding according to their similarities (here the kernel is noncentered and the first dimension of embedding should be neglected, see “Methods” section). f If we accommodate the node points on the circumference following the same ordering as the second dimension of embedding, we can again recover an unbroken circular pattern that resembles the angular coordinates of the original PSO model