A coarse-grained computational model of the nuclear pore complex predicts Phe-Gly nucleoporin dynamics

The phenylalanine-glycine–repeat nucleoporins are essential for transport through the nuclear pore complex. Pulupa et al. observe reptation of these nucleoporins on a physiological timescale in coarse-grained computational simulations.

Abstract

The phenylalanine-glycine–repeat nucleoporins (FG-Nups), which occupy the lumen of the nuclear pore complex (NPC), are critical for transport between the nucleus and cytosol. Although NPCs differ in composition across species, they are largely conserved in organization and function. Transport through the pore is on the millisecond timescale. Here, to explore the dynamics of nucleoporins on this timescale, we use coarse-grained computational simulations. These simulations generate predictions that can be experimentally tested to distinguish between proposed mechanisms of transport. Our model reflects the conserved structure of the NPC, in which FG-Nup filaments extend into the lumen and anchor along the interior of the channel. The lengths of the filaments in our model are based on the known characteristics of yeast FG-Nups. The FG-repeat sites also bind to each other, and we vary this association over several orders of magnitude and run 100-ms simulations for each value. The autocorrelation functions of the orientation of the simulated FG-Nups are compared with in vivo anisotropy data. We observe that FG-Nups reptate back and forth through the NPC at timescales commensurate with experimental measurements of the speed of cargo transport through the NPC. Our results are consistent with models of transport where FG-Nup filaments are free to move across the central channel of the NPC, possibly informing how cargo might transverse the NPC.

Introduction

In all eukaryotes, nuclear pore complexes (NPCs) facilitate the transport of biomolecular cargo across the barrier of the nuclear envelope. Each NPC is a ∼50-MD eightfold symmetric, cylindrical channel with its axis perpendicular to the nuclear envelope (Rout et al., 2000; Cronshaw et al., 2002; Alber et al., 2007a,b; Tamura et al., 2010; Tamura and Hara-Nishimura, 2013; Obado et al., 2016). NPCs are composed of ∼30 nucleoporin (Nup) proteins that exist in multiples of eight, totaling ∼500 total proteins (Alber et al., 2007a; Tamura and Hara-Nishimura, 2013). Although the nucleotide sequences of the Nup genes have diverged significantly over evolution, the basic architecture of the NPC has remained fundamentally conserved (Devos et al., 2004, 2006; Alber et al., 2007b; Brohawn et al., 2008; Franks et al., 2016).

The most studied NPCs are those from yeasts and vertebrates, both members of Opisthokonta, a taxon of the eukaryotes that includes fungi and metazoa (Adl et al., 2012; Obado et al., 2016). Opisthokont Nups are divided into three different classes: the pore membrane proteins (POMs), core scaffold Nups, and phenylalanine-glycine (FG)–repeat Nups (Devos et al., 2006; Alber et al., 2007b). POMs contain the trans-membrane domains that anchor the NPC to the nuclear envelope. Core scaffold Nups are the structural proteins that make up the major architecture of the NPC and most of its mass. These proteins anchor to the nuclear envelope and POMs. These scaffold Nups constitute four concentric rings, two inner adjacent rings sandwiched by two outer rings at the nucleoplasmic and cytoplasmic sides. Mounted onto the scaffold Nups are the phenylalanine-glycine–repeat nucleoporins (FG-Nups), whose filamentous, unstructured domains protrude into the lumen of this channel and compose the selectively permeable barrier (Fahrenkrog et al., 1998; Kiseleva et al., 2004). This barrier prevents nonspecific cargos transiting the NPC while allowing for the rapid transport of select cargos, with transport speeds as fast as thousands of events per pore per second (Moore and Blobel, 1993; Görlich and Kutay, 1999; Ribbeck and Görlich, 2001; Lei and Silver, 2002; Yang et al., 2004; Wälde and Kehlenbach, 2010).

Although the FG-Nups show divergence at the level of amino acid sequence, there are remarkably conserved regions of amino acid sequence that highlight the karyopherin (Kap)– and Nup-binding sites (Denning and Rexach, 2007). When the properties of FG-Nups were examined in vivo, the orientational rigidity was conserved between species (Atkinson et al., 2013). The filamentous domains of the FG-Nups of all species possess characteristic FG-repeat motifs, and a single NPC contains thousands of these repeat domains. The FG repeats can self-associate via hydrophobic interactions (Kraemer et al., 1994; Gustin and Sarnow, 2001; Frey et al., 2006; Frey and Görlich, 2007; Ader et al., 2010; Shabman et al., 2011; Simon and Rout, 2014). However, the reports of the strength of these interactions have varied over orders of magnitude (Patel et al., 2007; Satterly et al., 2007; Kuss et al., 2013; Rangl et al., 2013).

The FG-repeat domains bind to Kaps, chaperone complexes that mediate transport in and out of the nucleus (Radu et al., 1995; Wozniak et al., 1998). The binding of Kaps to nuclear localization signals (NLSs) or nuclear export signals enables selective translocation of cargo. Once cargo with an NLS reaches the nucleoplasmic side of the NPC, RanGTP disassociates it from the Kap. When cargo with an nuclear export signal reaches the cytoplasmic side of the NPC, RanGAP and Ran-binding proteins disassemble export complexes (Moore and Blobel, 1993; Görlich and Kutay, 1999; Lei and Silver, 2002; Smith et al., 2002). Kaps are largely conserved across eukaryotes, such that a rice karyopherin-β1 will transport GFP tagged with a viral (SV40) NLS in permeabilized HeLa cells (Jiang et al., 1998).

Despite the consensus on structure and functional components, there are numerous different models for the mechanism of selective transport. The selective phase model postulates that interactions between FG repeats on different FG-Nups lead to the creation of a cross-linked gel (Ribbeck and Görlich, 2002; Frey et al., 2006). Under this model, NLS cargo binds to a Kap and outcompetes FG–FG interactions for FG-binding sites. This competition results in the cargo melting into the meshwork of FG–FG filaments, enabling transport into the cell through repeated steps of binding and melting. The entropic exclusion model posits that the unstructured FG-Nups occupy space and prevent the passage of non-NLS cargo over a certain size (Rout et al., 2003). Because NLS cargo can bind FG-Nups, NLS cargo is capable of overcoming the entropic barrier of entering the pore, whereas non-NLS cargo will be excluded. The competition model of transport proposes that the disordered FG-Nups can exclude non-NLS cargo only when NLS cargo is present to cross-link FG-Nups by binding multiple FG repeats (Jovanovic-Talisman et al., 2009). The reduction-of-dimensionality model proposes that once a Kap binds to an FG-binding site, it can easily and rapidly switch from binding site to binding site (Peters, 2009). A Kap experiencing a two-dimensional random walk over the surface of the filament meshwork could be faster than the three-dimensional random walk of non-NLS cargo. The selective gating/collapse model maintains that the FG-Nups form a meshwork that prevents the diffusion of nonspecific cargo (Lim et al., 2007). When NLS-tagged cargo binds to the FG repeats, the corresponding FG-Nups undergo a conformational change that enables the cargo to enter the nucleus. The forest/tube gate/copolymer brush gate model suggests that the tips of some FG-Nups coalesce into a diffusive barrier in the center of the NPC, whereas their “stalks” form an extended bush zone along the periphery. Under this model, the FG-Nups behave in a “tree-like” manner and provide a diffusive landscape that can be penetrated by the transport factors, but not by other macromolecules (Yamada et al., 2010; Ando et al., 2014). Additionally, the diameter of the pore has also been suggested to change to allow the passage of cargo with NLS (Solmaz et al., 2013). An alternate model of transport suggests that cargo translocation can occur via a “Brownian ratchet,” whereby a given FG-Nup binds to the Kap–cargo complex on one side of the nuclear envelope (Simon et al., 1992; Mincer and Simon, 2011). This cargo then diffuses through the NPC, bound to the same FG-Nup or a restricted set of FG-Nups. When the cargo reaches the opposite side of the nuclear envelope, Ran-GTP or RanGAP and Ran-binding proteins sever the bond between the FG-Nup and the cargo, effectively preventing the cargo from diffusing back across.

Even though little agreement exists on the mechanism of cargo transport, most models posit a critical role for the FG-Nups. Although recent structural work has allowed localization of individual Nups within the mammalian NPC (Stuwe et al., 2015; Kosinski et al., 2016; Lin et al., 2016; von Appen and Beck, 2016), the dynamics of the FG-Nups remain elusive. Characterizing these FG-Nups could be essential for elucidating the mechanism of NPC transport. The in vivo study of these FG-Nups is severely limited by their unstructured domains, symmetries, and packing within the NPC.

Computational simulations of the entire NPC and its components have provided insight into the potential dynamics and interactions within the NPC. Molecular dynamics simulations explored the nature of interactions between FG-Nup domains and between FG-Nups and Kaps (Miao and Schulten, 2010; Gamini et al., 2014). Unfortunately, molecular dynamics simulations are currently limited by timescales to under a microsecond, whereas transport occurs on a millisecond timescale. In addition, these simulations cannot yet recapitulate the complexity of the NPC with its multiple rings of proteins. Therefore, many groups have used coarse-grained simulations to either reach the timescales of transport or incorporate the complexities of the NPC. The NPC is amenable to coarse-grained computational modeling as a macromolecular machine, because many of its biophysical properties, such as the anisotropy of FG-Nups at various locations along their length (Atkinson et al., 2013), the approximate locations of their anchor regions and the arrangements of other Nups (Alber et al., 2007a), approximate Nup stoichiometry (Rout et al., 2000; Cronshaw et al., 2002; Rabut et al., 2004), and predicted binding of FG-Nups with Kaps, are reported in the literature (Bayliss et al., 1999, 2002a,b; Patel et al., 2007; Kapinos et al., 2014). We have previously modeled the nuclear pore without invoking an a priori mechanism of transport using generic homogeneous FG-Nups arranged in rings of eightfold symmetry that were evenly spaced through the cylindrical pore (Mincer and Simon, 2011). To characterize the local environment of the NPC and probe the electrostatic potential of the pore, some groups have used coarse-grained amino acid sequences to render predicted electrostatic fields and predict cargo’s interactions with these fields (Tagliazucchi et al., 2013; Ando et al., 2014). More recently, the role of “like charge regions” in the formation and regulation of the selective barrier of the NPC has been studied, suggesting that positive like charge regions play a role in enabling FG-Nups to maximize interactions and cover a larger space within the lumen of the NPC (Peyro et al., 2015a,b). Likewise, simulations suggest the hydrophobic and electrostatic properties of the amino acid sequences of FG-Nups contribute to the arrangement of the filament mass within the lumen of the NPC (Ghavami et al., 2014). Other coarse-grained models probe cargo translocation through the pore, attempting to capture the necessary components of a selective transport mechanism (Zilman et al., 2007; Mincer and Simon, 2011; Moussavi-Baygi et al., 2011). Even though these simulations attempt to capture the dynamics of the pore, many assume that FG-Nup filaments are tethered at uniform positions inside the scaffold of the NPC and that binding sites are distributed homogenously along the FG-Nup filaments (Zilman et al., 2007; Mincer and Simon, 2011; Moussavi-Baygi et al., 2011), which may obfuscate the underlying molecular interactions and the dynamics of the FG-Nups. More recent simulations have explored the interactions of FG-Nup filaments with each other and with Kaps (Vovk et al., 2016; Zahn et al., 2016), yielding different results for how FG-Nups might behave in the lumen of the NPC. Coarse-grained modeling of FG-Nup filaments tethered in the NPC suggests highly FG-Nups enable the maintenance of a diffusive barrier through their rapid Brownian motion (Mincer and Simon, 2011), reconstructing itself mere microseconds after a local disruption by a cargo (Moussavi-Baygi and Mofrad, 2016).

Because a single transport event occurs on the timescale of many milliseconds, our goal was to have a model that was sufficiently coarse-grained to simulate over the timescale of a second to cover multiple transit events. Because the yeast NPC has been comprehensively characterized on an architectural level, we used it to determine FG-Nup anchor site locations, filament lengths, FG-repeat binding site positions, and densities of FG-Nups. The geometry and FG-Nup sequences used in our model are similar to the conditions by Tagliazucchi et al. (2013) in their coarse-grained simulation of the NPC. The transit rates for individual cargos have been reported to be on the order of milliseconds (Dange et al., 2008; Sun et al., 2008; Tu and Musser, 2011). Our mesoscale model allows us to reach timescales 10²–10³ longer than the transit rate. To ensure that our model behaved in a biologically relevant fashion, we compared a single simulated filament to published values of radius of gyration (R_g) and end-to-end measurements. We also compared the autocorrelation functions of the orientation of the filaments during the full simulation to in vivo anisotropies of FG-Nups previously measured in our laboratory.

Our results suggest the FG-Nup network is highly dynamic at a timescale of hundreds of milliseconds, with considerable freedom in the movements of the FG-Nups. These results are robust even when the strength of the FG-Nup bonds is varied over orders of magnitude. Notably, we observe portions of the FG-Nup filaments translocating through the NPC with speeds commensurate with the rates at which single cargo translocate the pore and at rates sufficient to recapitulate the rates of cargo transport.

Materials and methods

Dynamics

The dynamics of each FG-Nup are modeled using the pairwise agent interaction with rational superposition (PAIRS) model (Alberts, 2009). The positions and orientations of these filament segments make up the coarse-grained degrees of freedom, thereby encompassing and eliminating the solvent degrees of freedom.

When any two FG-repeat sites collide, they can bind if they are not already bound to other FG sites. The strength of the bond formed is modulated by increasing or decreasing the off rate of the FG–FG bond, a parameter of the simulation. The off rate is stochastic, and is expressed as number of bonds dissociated per second. Varying the FG–FG off rate over several orders of magnitude modulates FG–FG cross-linking, which allows the investigation of the influence of cross-linking on filament dynamics and flexibilities.

Filament segments experience five forces: (1) PAIRS forces that are responsible for ensuring that the FG-Nup behaves like a flexible filament, (2) repulsion forces resulting from interactions with the pore geometry, (3) adhesion forces between segments “bound” to each other, (4) repulsion forces resulting from collisions with other filament segments, and (5) Brownian forces. The forces between “bound” segments and the interactions with pore geometry are new to this iteration of our model; however, the PAIRS forces, repulsion forces, and Brownian forces remain unchanged from the previous model.

At a given time step during the course of our simulation, two adjacent segments on the same filament may become temporarily disconnected because of other forces. The PAIRS algorithm analytically determines the displacement necessary to reconnect the adjacent ends within one time step. Moreover, these adjacent filament segments are rotated to maintain a prescribed angle between them. The PAIRS forces have associated damping coefficients, which serve as a tuning mechanism to achieve desired filament flexibility. In addition to becoming disconnected, adjacent FG-Nup segments may temporarily overlap. The PAIRS algorithm also displaces segments to resolve overlap. Thus, in this model, a filament comprises a collection of rigid cylindrical filaments where adjacent segments are connected through a translational and rotational spring. The PAIRS algorithm provides a correction to the Euler time integration scheme to solve the system of differential equations for the filament dynamics along with algebraic constraints corresponding to setting the strain in both the translational and rotational springs is zero (Andrews, 2014).

FG-repeat sites

FG-Nup–repeat sites are fixed relative to the center of mass of the segment. Placement of FG repeats on particular segments and their positions on segments are determined by overlaying the primary amino acid sequence for the particular FG-Nup on the segmented filament and then performing a search for FxFG, FG, GLFG, and PxFG (where x is any amino acid). An FG site was then placed in the middle of the FG sequence. Hydrophobic interactions between different FG repeats (either on different or the same filaments) are modeled as bonds that behave as harmonic springs with an equilibrium bond ($r_b=$ 0.6 nm) length equal to the twice the radius of the filament. When the distance between two FG-repeat sites is less than 0.9 nm, three times the filament radius a bond is formed. In the event that there are multiple FG-repeat sites within 0.9 nm of a particular FG-repeat site, one of them is randomly chosen to form a bond with the FG-repeat site.

All bonds dissociate stochastically based on a predetermined off rate set at the start of the simulation. Because the FG-repeat sites do not necessarily coincide with the center of mass of the corresponding filament segment, the forces caused by these springs also result in a torque on the participating segments. Bonds are not allowed to form between FG sites on adjacent segments on the same filament. We enforce this condition, as we believe that these interactions are sterically unfavorable.

The following describes binding between two segments:

Allow ${\overrightarrow{x}}_{b,1}$ and ${\overrightarrow{x}}_{b,2}$ to be two binding sites bound to each other. Let ${\overrightarrow{y}}_i$ and ${\overrightarrow{y}}_j$ be the center of mass of segments i and j corresponding to the binding sites ${\overrightarrow{x}}_{b,1}$ and ${\overrightarrow{x}}_{b,2},$ respectively. The forces ${\overrightarrow{F}}_i$ and ${\overrightarrow{F}}_j$ caused by this FG–FG interaction are given by

$${\overrightarrow{F}}_i=k\left(\mathrm{ }\Vert {\overrightarrow{x}}_{b,2}-\mathrm{ }{\overrightarrow{x}}_{b,1}\Vert -r_b\right)\frac{\left(\mathrm{ }{\overrightarrow{x}}_{b,2}-\mathrm{ }{\overrightarrow{x}}_{b,1}\right)}{\Vert \mathrm{ }{\overrightarrow{x}}_{b,2}-\mathrm{ }{\overrightarrow{x}}_{b,1}\Vert }$$

$${\overrightarrow{F}}_j=k\left(\mathrm{ }\Vert {\overrightarrow{x}}_{b,1}-\mathrm{ }{\overrightarrow{x}}_{b,2}\Vert -r_b\right)\frac{\left(\mathrm{ }{\overrightarrow{x}}_{b,1}-\mathrm{ }{\overrightarrow{x}}_{b,2}\right)}{\Vert \mathrm{ }{\overrightarrow{x}}_{b,1}-\mathrm{ }{\overrightarrow{x}}_{b,2}\Vert },$$

where the spring constant, k = 10³ pN/nm, is unchanged from the previous model. The torque on the corresponding segments is

$${\overrightarrow{T}}_i=\left({\overrightarrow{x}}_{b,1}-{\overrightarrow{y}}_i\right)\times {\overrightarrow{F}}_i$$

$${\overrightarrow{T}}_j=\left({\overrightarrow{x}}_{b,2}-{\overrightarrow{y}}_j\right)\times {\overrightarrow{F}}_j.$$

Interaction with geometry

The filament segments are not allowed to collide with either the NPC scaffold or the nuclear envelope. These collisions are prevented in two ways. When the segment is outside the lumen of the NPC and the calculated displacement would cause the segment to overlap the nuclear envelope, movement is only allowed perpendicular to the nuclear–cytoplasmic axis. This prevents collisions with the membrane. When the segment is inside the lumen of the NPC and the calculated displacement would cause the segment to overlap with the scaffold of the NPC, displacement is only allowed parallel to the nuclear–cytoplasmic axis.

Implementation

The strength of the FG-bond off rate was assessed over several orders of magnitude: FG4 = 10⁴/s, FG5 = 10⁵/s, FG6 = 10⁶/s, FG7 = 10⁷/s, and FG_off = 10^∞/s. At each time step for all binding conditions, FG repeats are checked to see which are close enough to form a bond. In the case of FG_off, the binding algorithm is not entered.

However, in the case of FG4, FG5, FG6, and FG7, a bin sort (described in detail in the following section) was performed, and bonds were made or broken.

Bin sort FG-FG–binding scheme

At each time step, FG repeats are checked to see which are close enough to form a bond. A priori one may think to compare each FG-repeat location with every other one when determining whether a given FG repeat is in the vicinity of a potential binding partner. This scheme, however, results in a large computational cost that makes it infeasible to run simulations to the biological timescale of interest. The computational cost (number of operations) scales as the square of the number of FG-repeat sites in this scheme, referred to as “order N-squared,” or O(N²) (Knuth, 1998).

A more efficient method involves bin sorting (Knuth, 1998). Specifically, FG-repeat sites are sorted into bins of size 1 nm in each direction. The search for possible bonding partners for a given FG repeat then becomes local, and consequently, this data structure enables checking for bonds with computational cost that is on the order of the number N of FG repeats, referred to as “order N,” or O(N). Because the FG–FG interactions are in fact local and do not extend over a larger spatial range, the resulting dynamics are equivalent to the O(N²) method.

The pseudocode for this process is as follows: step 1: bin sort all FG repeat sites; step 2: shuffle the list of FG-repeat sites; step 3: loop over the shuffled list of FG-repeat sites; step 4: determine the bin j in which FG-repeat site i resides; step 5: store FG-repeat sites that reside in either bin j or reside in bins m, which share a vertex with bin j, in a temporary array; step 6: shuffle this temporary array; and step 7: check for binding criterion for each FG repeat site in this list.

The magnitude of speed-up achieved with the bin sort method is significant. 5,000 iterations of the algorithm (corresponding, for a 2-ns time step, to 10 μs of simulation time), took 64.3 s for the bin sort method as opposed to 43,182.4 s for the naive O(N²) implementation.

Anisotropy and autocorrelation functions

Anisotropy and autocorrelation functions are both measurements of the orientational freedom of molecules. The relationship between these measurements can be formalized by the Perin equation:

$$\frac{{\mathrm{r}}_0}{\mathrm{r}}=1+\raisebox{1ex}{$\tau $}\!\left/ \!\raisebox{-1ex}{$\Theta $}\right.,$$

where τ is the fluorescence life span, θ is the rotational correlation time, r is the measured anisotropy, and r₀ is the fundamental anisotropy (the anisotropy of the probe in a fixed position). Faster decay of autocorrelation functions correlates with a lower measured anisotropy value, and longer decay of autocorrelation functions correlates with a higher measured anisotropy value.

We have previously measured the anisotropy of Nups in their native context inside the NPC. This approach was taken because we found that Nups in the NPC showed altered anisotropy when we changed their location in the NPC and much lower anisotropy when they were expressed elsewhere in the cell, outside of the packing in the NPC (Atkinson et al., 2013). We evaluated their orientation and dynamics by inserting fluorescent probes at several points along the unstructured domain of the FG-Nups and measuring the fluorescence anisotropy at the different positions (Mattheyses et al., 2010; Kampmann et al., 2011; Atkinson et al., 2013). Fluorescent anisotropy experiments are performed by exciting fluorophores with a given linear polarization of light. By measuring the light emitted parallel to the excitation and the light emitted perpendicular to the excitation, one can calculate a fluorophore’s anisotropy, or its orientational freedom. The measured anisotropy is directly related to the rotational correlation time.

To compare these experimental results to our coarse-grained model, we needed a method to measure orientational flexibility in our simulation. We calculated the autocorrelation function, a measure of orientational self-correlation, which can be calculated for a single filament segment over the time course of the entire experiment as follows:

$$f\left(k\right)= \frac{1}{(n-k)}\cdot {\displaystyle \sum }_{t=1}^{n-k}\left({\overline{u}}_t\right)\cdot \left({\overline{u}}_{t+k}\right) ,$$

where k represents the difference in time, n represents the total number of data points, and ${\overline{u}}_t$ represents the orientation unit vector at time t. In an ideal case, this autocorrelation is expected to approximate a single exponential decay, the half-life of which should be directly correlated to the decay of anisotropy that a fluorescent probe placed along the filament length should experience. Therefore, a faster decay in the autocorrelation function is equivalent to a lower anisotropy, and a longer decay in the autocorrelation function is equivalent to a higher anisotropy.

Nematic order parameters

The nematic order parameter is used to characterize the orientational order in liquid crystals. It is calculated by taking the largest positive eigenvalue from a second order orientational descriptor, Q (Eppenga and Frenkel, 1984).

Q takes the form of a three-by-three second-order tensor, where each element, Q_αβ, is defined as follows by α and β, which represent x, y, and z:

$$Q_{\alpha \beta }=\frac{1}{2\times N}\left(\left(3\times {\displaystyle \sum }_i {\overline{u}}_{i\alpha } \times {\overline{u}}_{i\beta }\right)-{\delta }_{\alpha \beta }\right) ,$$

where N represents the number of segments, ${\overline{u}}_{i\alpha }$ is the α component of the orientation unit vector of the i^th segment, and ${\delta }_{\alpha \beta }$ is the Kronecker delta function. The nematic order parameter is always between 0 and 1, with 1 indicating the maximal order and 0 indicating complete disorder.

Analysis

All analysis and visualization was performed using the software MATLAB (MathWorks).

Online supplemental material

Video 1 shows a single translocation event of FG-Nup49 filament under the FG_off-binding condition.

Results

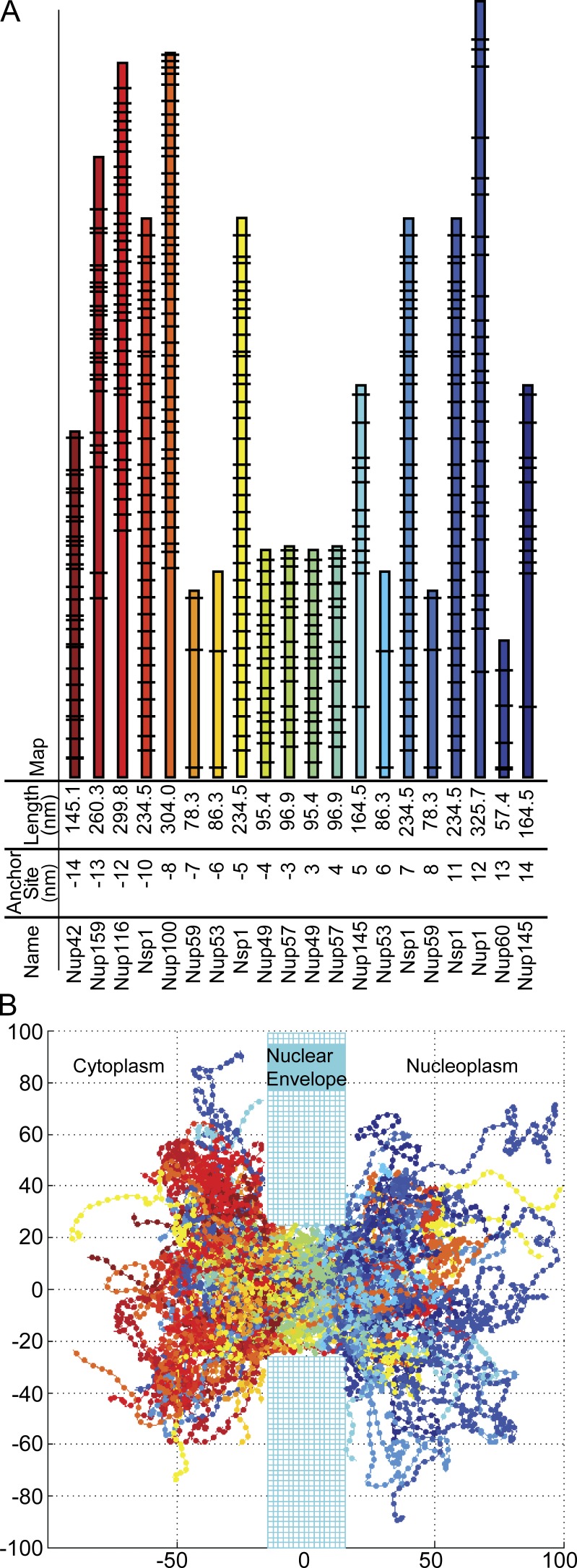
The model space was three dimensional and encompasses a single cylindrical NPC, embedded in a wall representing the nuclear envelope and continuous on each side with hemispheres representing the nucleoplasm and cytoplasm in which filamentous FG-Nups and cargo can freely diffuse (Fig. 1 B). This current model was constructed to more accurately recapitulate the known morphology of the NPC. The NPC itself is modeled as a cylinder of 30 nm in length and 50 nm in inner diameter, dimensions consistent with the approximate size of the yeast NPC (Alber et al., 2007a). Twenty rings of FG-Nups anchored in eightfold symmetry are located at the approximate in vivo positions determined experimentally (Alber et al., 2007a; Tagliazucchi et al., 2013). The length of each filament and the location of FG-repeat sites along its length are determined from the primary amino acid sequences of the predicted unfolded regions (Yamada et al., 2010), except for Nup53 and Nup59, which were defined by the largest continuous amino acid sequence containing the FG motifs FxFG, GLFG, FG, and FxF, separated by ∼100 amino acids and including 10 amino acids at the terminus of the domain (Yamada et al., 2010; Tagliazucchi et al., 2013).

Figure 1.

The geometry of the model NPC. (A) The anchor site of each NPC filament indicates the attachment position along the nuclear–cytoplasmic axis of each FG-Nup with the NPC geometry. The lengths of FG-Nups correspond to the size of the unstructured portions of the primary amino acid sequence. The black lines indicate FG-repeat locations. These FG-Nups are found in eightfold symmetry, anchored around the scaffold of the NPC. (B) Plotted snapshot of our simulation; all axes are in nanometers.

Each FG-Nup is modeled as a flexible filament anchored to the interior surface of the NPC cylinder. In this model, each FG-Nup is subdivided into the appropriate number of rigid cylindrical filaments segments of length 4 nm and radius 0.3 nm to reach the predicted length based on the amino acid sequence. The radius of 0.3 nm was chosen, because the radius of an amino acid chain averaged over all amino acids is on the order of 0.3–0.4 nm (Counterman and Clemmer, 1999).

A coarse-grained Nsp1 filament composed of 4-nm segments recapitulates the end-to-end distances from molecular dynamics simulations for packed filaments. In Miao and Schulten (2009), the authors divided the 600 amino acids of Nsp1 into 25 100–amino acid fragments and then tethered these segments onto a plane such that the tethered endpoints formed a 5 × 5 lattice. These filament segments collapsed into a brush structure, with a height of ∼8 nm. Therefore, the expected end to end from these simulations of Nsp1 in a packed environment would be 48 nm. In our simulations, the R_g of a single tethered Nsp1 filament with FG_off binding is 21.2 nm (radius of hydration [R_H] = 16.9 nm) and the R_g of a tethered Nsp1 of FG4 binding is 19.3 nm (R_H = 15.5 nm). The end-to-end distance of our tethered Nsp1 filament is 49.7 nm in the absence of FG–FG binding and 43.5 nm in the presence of FG4 binding. The R_g of a single untethered Nsp1 filament with FG_off binding is 21.1 nm (R_H = 16.8 nm), and the R_g of an untethered Nsp1 of FG4 binding is 19.9 nm (R_H = 16.0 nm). The end-to-end distance of our untethered Nsp1 filament is 50.0 nm in the absence of FG–FG binding and 47.1 nm in the presence of FG4 binding. These values are in close agreement to the value of 48 nm from the molecular dynamics of Miao. These results differ from a coarse-grained single isolated filament simulation, where the end-to-end distance for NSP1 was 24 nm (Peyro et al., 2015a). However, we believe that our filaments behave most similarly to those in a confined volume. Miao and Schulten (2009) note that the array forms a brush-like structure with a height far larger (∼8 nm) than the R_g of a single chain, which they measure at 1.4–2.0 nm (for a 100–amino acid segment). Similarly, in a coarse-grained model of the NPC, the R_g of FG-Nups within the NPC was shown to be 3.9 to 6.5 times greater than R_g of isolated filaments (Ghavami et al., 2014). According to an MD simulation of full-length NSP1 the R_g is 6.5 nm (Gamini et al., 2014), meaning that our measurement of ∼20 nm is reasonable for an R_g of a packed FG-Nup. These results are consistent with our own experimental results, where the FG-Nups anchored inside the NPC exhibited a higher effective persistence length than the FG-Nups artificially anchored to the plasma membrane, which demonstrated very high flexibility, suggesting that polymer dynamics are strongly influenced by the local environment (Atkinson et al., 2013).

Modulating FG–FG interactions creates different diffusive barriers

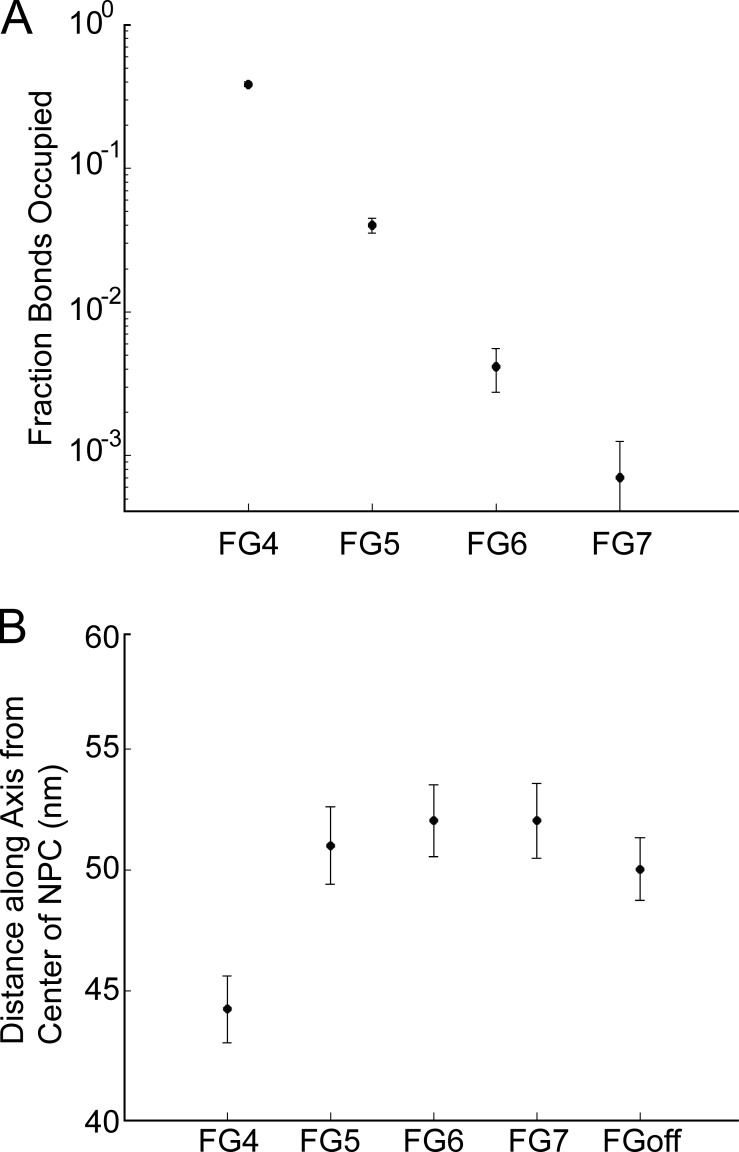
In the simulations the density and distribution of both the FG-Nup filament segments and the FG-repeat sites were studied as a function of FG–FG binding by varying the FG–FG off rate over several orders of magnitude. The fraction of FG-repeat sites occupied was determined for the various binding conditions of the simulation (Fig. 2 A). At the strongest FG-binding condition probed, FG4, approximately one third of the FG–FG–binding sites were occupied with FG–FG bonds. In a much weaker binding condition, FG7, only a maximum of 0.3% of binding sites were occupied at any one time. These disassociation rates remained constant over the total simulation time, which was a hundred milliseconds. The density of FG-Nups within the NPC lumen decreased with binding strengths weaker than FG4 (Fig. 4 F). The FG–FG bond strength also affected the packing of filaments. We measured packing as the distance from the center of the pore along the axis within which 75% of filament mass was contained (Fig. 2 B). In the FG4 condition, the mass of filaments was closer within the NPC channel (Fig. 2 B). With weaker bonds, the FG-Nups extended farther outside of the lumen of the NPC into the cytoplasm and nucleoplasm. On average, 75% of the filament mass was within 44 ± 1 nm (FG4) or 52 ± 2 nm (FG7) of the center of the NPC.

Figure 2.

Modulating FG–FG–binding strength changes arrangement of FG-Nups. (A) The fraction of FG-binding sites occupied at a given time step. (B) Distance from the center of the NPC lumen that 75% of filament mass is located within. All plots are mean ± SD.

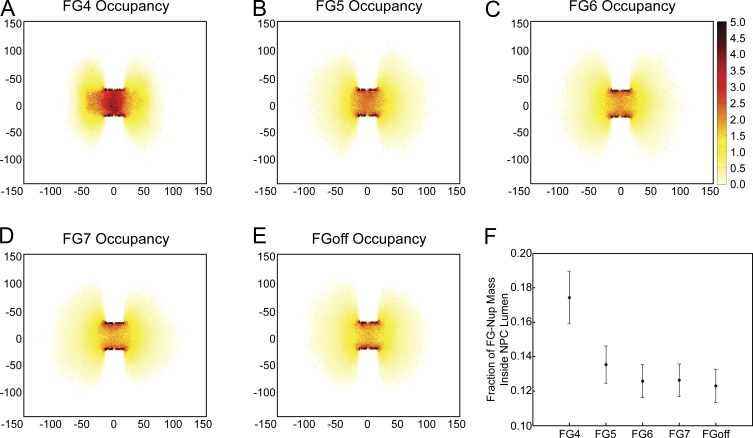
Figure 4.

FG-Nup packing creates channel in the center of the lumen. Two-dimensional histogram of filament locations normalized over a 100-ms simulation in a 4-nm slice through the center of the NPC under FG4 bond strength (A), FG5 bond strength (B), FG6 bond strength (C), FG7 bond strength (D), and no FG bonds (E). The scale goes from 0 to 5 and indicates the mean number of filaments in that spot over the time course of the simulation. (F) The fraction of filament mass that is located within the lumen of the NPC. Plot is mean ± SD.

Simulated FG-Nups experience similar orientational freedoms as in vivo FG-Nups

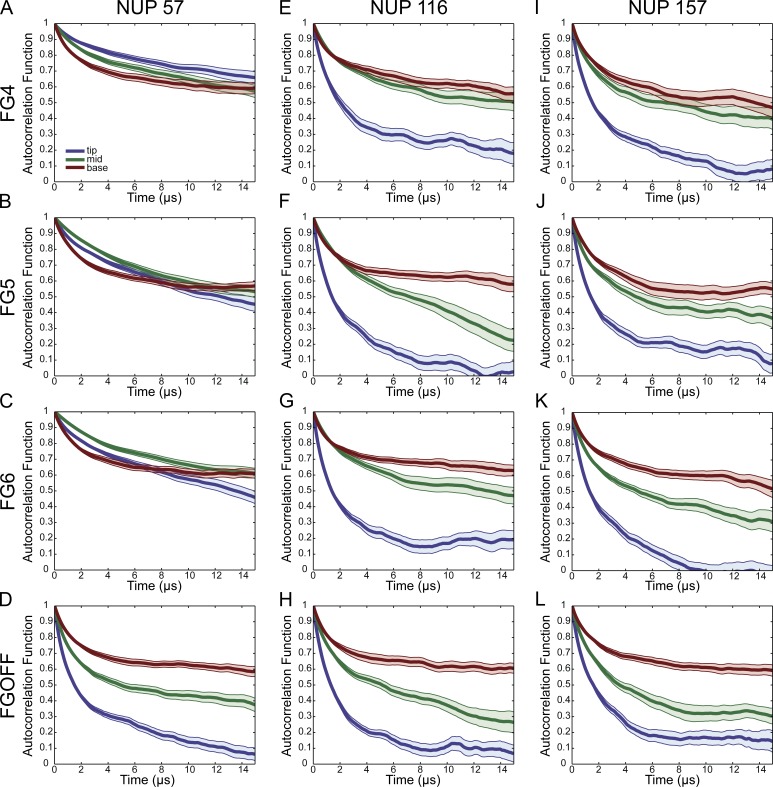
To test whether the simulations of the FG-Nup filaments in this model quantitatively recapitulate experimental measurements, the autocorrelation functions of Nup116, Nup57, and Nup159 were calculated and averaged across four iterations of a given simulation (Fig. 3). We have previously measured anisotropy at the base and tip for each of these FG-Nups and at the base, middle, and tip for Nup116 and Nup159. The decay constant and anisotropy are directly related via the Perrin equation (see Materials and methods, “Anisotropy and autocorrelation function”). We previously observed no difference in anisotropy between a probe positioned at the base or at the tip of Nup57 (96.9 nm). Conversely, for both Nup116 (299.8 nm) and Nup159 (260.3 nm), probes placed at the base, middle, and tip of the FG region yielded a clear difference in measured anisotropy, with the most flexibility observed at the tip, an intermediate flexibility observed at the middle, and a low flexibility observed at the base. These anisotropy measurements were taken both in the presence and the absence of Kaps, which were removed in a digitonin permeabilized system. There was no difference in anisotropy measurements upon the removal of Kaps (Atkinson et al., 2013).

Figure 3.

The orientational rigidity of FG-Nups exhibit differential dependence on FG–FG bond strength. Autocorrelation plots of filaments, taken at three locations along filament length, base, middle, and tip. (A–D) FG-Nup116, (E–H) FG-Nup57, and (I–L) FG-Nup159, each at four different FG–FG off rates (FG4, FG5, FG6, and FG_off). Plotted lines represent mean of autocorrelation functions ± standard error. Blue, tip segment; green, middle segment; red, base segment.

In the case of the FG_off simulations, for all FG-Nups, the orientational freedom was lowest near where the filament was anchored and increased toward the tip of the filament (Fig. 3). This increase in orientational freedom was evident because near the tip the autocorrelation curve decayed faster and its asymptote was lower. Nup116 and Nup159 exhibited this trend regardless of the strength of the FG bonds. In contrast, Nup57 behaved differently from the others: when FG–FG bonding was allowed, no difference in the orientational rigidity along its length was observed. Each of these observations was consistent with our previous experimental results.

Distribution of FG-Nups in the lumen of the NPC

The density profiles of FG-Nups within a 4-nm transverse slice through the center of the pore (Fig. 4) were calculated. The greatest density of filaments was located along the periphery of the NPC lumen, and density decreased moving radially toward the center of the NPC, resulting in a central channel of decreased density. This central channel was more prominent with FG–FG bonds of a lower stability. These results are consistent with the findings of Tagliazucchi et al. (2013) in their simulation of the pore using static potential of mean force calculations. The bulk of the simulated FG-Nups explore a region outside of the lumen of the pore because of the volume of the open space on either side of the NPC, similar to the simulations of Tagliazucchi et al. (2013). Increased stability of FG–FG binding increases the cross-linking of filaments within the pore, decreasing the prominence of this central channel. Interestingly, we did not observe the well-defined “doughnut-like” region of FG-Nups that was observed in the simulations of Ghavami et al. (2014). This could be attributed to differences in anchor locations between the two simulations and the lack of charged residues in our simulation that they argue pushes the FG-Nup mass toward the center of the NPC channel.

FG-FG bonds occupy the lumen of the NPC

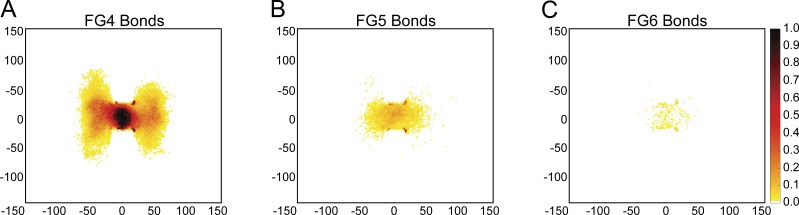
In each of the FG binding conditions, the majority of the FG–FG bonds are within the lumen of the NPC (Fig. 5). In FG4, a mean of 650 bonds populates the lumen of the NPC. These bonds increase FG-Nup mass within the lumen and thereby reduce the prevalence of the central channel discussed in the previous section. In weaker binding conditions, this reduces not only the number of bonds but also their localization to the lumen of the NPC, resulting in a more prominent central channel of decreased FG-Nup density.

Figure 5.

FG–FG bonds are most concentrated in the interior of the NPC. Two-dimensional histogram of FG–FG bonds normalized over a 100-ms simulation in a 4-nm slice through the center of the NPC under FG4 bond strength (A), FG5 bond strength (B), and FG6 bond strength (C). The scale goes from 0 to 1 and indicates the probability of an FG–FG bond existing in that spot at any given time point in the simulation.

Nematic order inside the NPC decreases with stronger FG–FG interactions

Previously, behavior resembling a liquid crystal was observed for FG-Nups in the in vivo NPC (Atkinson et al., 2013). The FG-Nups showed a higher degree of anisotropy, or orientational order within the pore, similar to the orientational order of fatty acid tails in a lipid membrane. This order was affected by the location of each FG-Nup within the NPC and was significantly reduced when the FG-Nups were outside the lumen of the NPC. The anisotropy, or orientational order was highest near the base of the FG-Nups and decreased toward the tips of the filaments. These observations are consistent with the FG-Nups in the interior of the pore acting in an orientationally ordered manner (i.e., aligning along the nuclear–cytoplasmic axis).

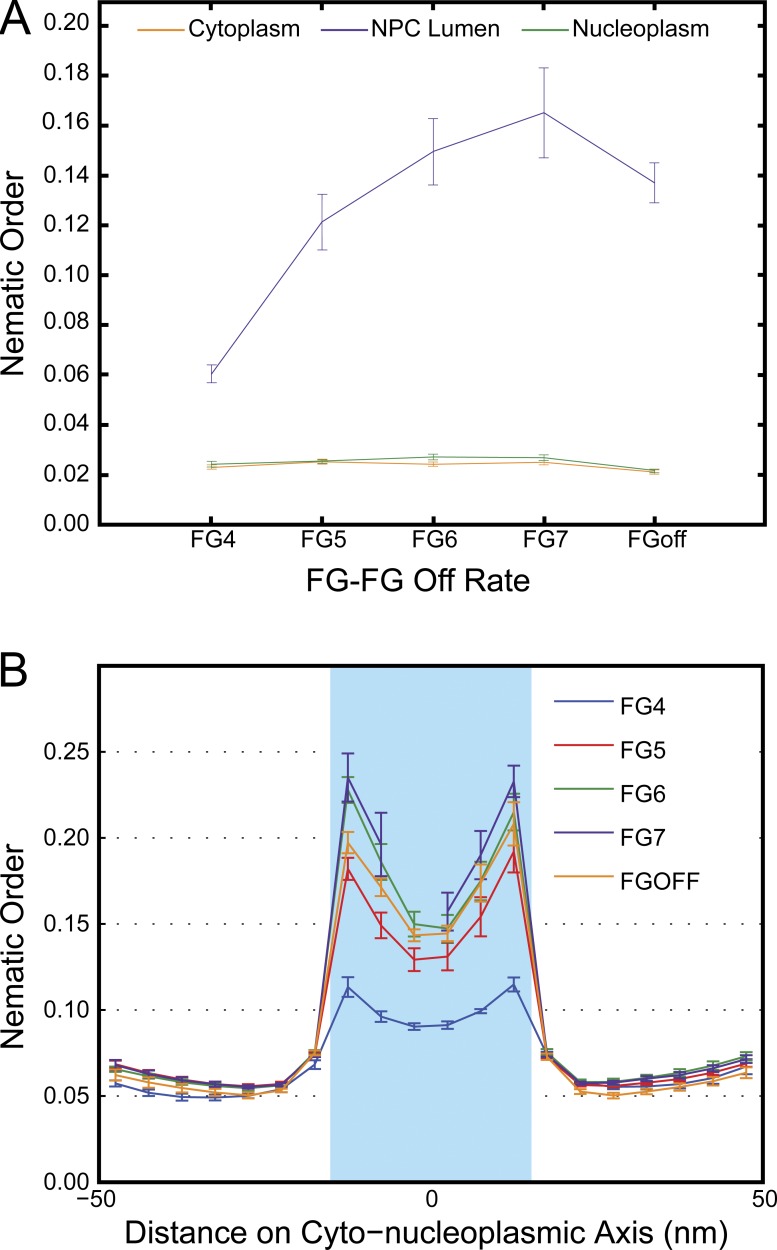
The nematic order parameter was calculated for the FG-Nups. The first five segments along a filament were not included in calculations to avoid the effects of the anchoring domains. In the lumen of the NPC, the nematic order parameter was inversely proportional to the FG–FG bond strength: the stronger the binding, the weaker the orientational order (Fig. 6 A). In the case of high FG–FG bond strength, many bonds were formed, as discussed in the previous section, effectively packing FG-Nups into the lumen. This held them in a denser meshwork that was only loosely organized according to orientation. At weaker FG–FG bond strengths, the filaments were not as restrained with the pore by FG interactions. Instead, the filaments were relaxed into a liquid-crystal–like state, with higher nematic order organization along the nuclear–cytoplasmic axis.

Figure 6.

Nematic orders are highest in the lumen of the NPC. (A) Nematic order parameters calculated inside and outside of the NPC lumen, averaged over four datasets of 100 ms. With decreasing FG-Nup–binding strength, increased nematic order within the NPC is observed. (B) Nematic order parameters were calculated across the nuclear–cytoplasmic axis (x axis is in nanometers) and averaged over four datasets of 100 ms. All plots are mean ± SD.

Across all FG–FG–binding conditions, the nematic order parameter for the filaments was greater within the NPC lumen relative to outside (Fig. 6 A). When the nematic order parameter was calculated over the entire lumen of the pore, the nematic order was substantially different for conditions of high binding (FG4 with a nematic order of 0.060 ± 0.004) and conditions of very low binding (FG7 with a nematic order of 0.17 ± 0.02). Interestingly, the nematic order was higher for FG7 than for FG_off, which may indicate that a certain amount of FG–FG binding may contribute to order within the NPC. For each binding condition, the nematic order was significantly higher inside the lumen than in the cytoplasm or nucleoplasm.

When the nematic order parameter was calculated in 5-nm increments along the nuclear–cytoplasmic axis, higher values were obtained there than for the entire lumen because of increased local order. For FG4, the nematic order within the NPC ranged from 0.090 ± 0.002 to 0.115 ± 0.004, and for FG7, the nematic order within the NPC ranged from 0.16 ± 0.01 to 0.24 ± 0.01 (Fig. 6 B). Interestingly, for each binding strength, the highest order within the NPC lumen occurred near the peripheries near the cytoplasm and the nucleoplasm, with a local minima in the center of the NPC.

FG-Nup filaments translocate the NPC

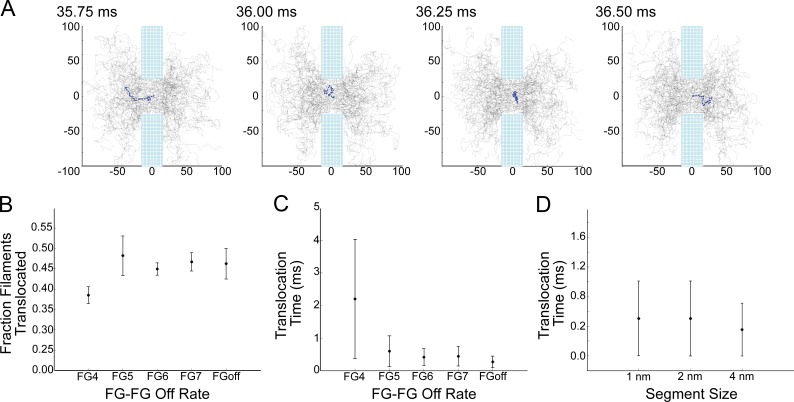
In all of the simulations, FG-Nup filaments translocate the NPC moving between the cytoplasmic and nuclear domains (Fig. 7 A and Video 1). Almost half of the FG-Nup filaments that started outside of the lumen of the NPC on the cytoplasmic side reached the nucleoplasm within the course of a 100-ms simulation time (Fig. 7 A). For FG4, 38.5% of filaments initially in the cytoplasm reached the inside of the nucleus during the course of the simulation. For FG5–FG 7 and FG_off, the translocation fraction was higher (Fig. 7 B).

Figure 7.

Filaments translocate the nuclear envelope. (A) Translocation event of a single FG-Nup49 filament under the no FG-bonding condition; all axes are in nanometers. (B) For all binding conditions, the fraction that translocate is defined as the fraction of filaments that started the simulation on the cytoplasmic side of the NPC and eventually made it into the nucleus. (C) Time to translocate is defined as the time elapsed between entering the NPC on one side and emergence on the opposite side, in either direction. (D) Time to translocate for filaments composed of segments of different sizes. All plots are mean ± SD.

Translocation time was measured as the time elapsed from the last moment at which the filament was located outside the lumen of the NPC on one side (nuclear or cytoplasmic ±15 nm) to the first time point the filament was located outside the lumen of the NPC on the opposite side (cytoplasmic or nuclear ±15 nm). The mean translocation time was shorter with faster FG–FG off rates. For FG4, the translocation time was 2.2 ms ± 1.8 ms. Without FG–FG bonding, the mean translocation time was 0.27 ± 0.13 ms. To confirm that the translocations were not an artifact of our segment length, we simulated shorter filament segments and observed translocations at indistinguishable timescales for FG_off (Fig. 7 D).

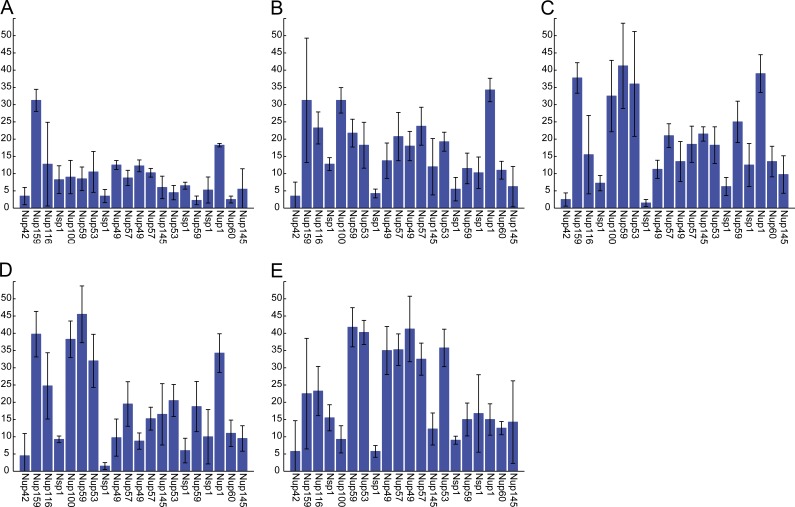
The number of translocation events per unit time increased with increasing off rates for FG–FG bonds, with the highest rate occurring in the absence of FG–FG bonding. Much of this increase was caused by the greater frequency of translocations of Nup57 and Nup49, two relatively short centrally located FG-Nups that contain many FG repeats (Fig. 8).

Figure 8.

The number of translocations per ring increases with increasing FG–FG off rates. (A–E) Number of translocations per ring of 8 FG-Nups, averaged over four datasets of 100 ms. All plots are mean ± SD. (A) FG4 bond strength. (B) FG5 bond strength. (C) FG6 bond strength. (D) FG7 bond strength. (E) FG_off bond strength.

Discussion

Selective transport across the nuclear envelope through the NPC is an essential part of eukaryotic life. Although models have been proposed to explain this phenomenon, distinguishing between these models has proved challenging, in part because they have been articulated in qualitative terms, precluding validation or refutation by experimental evidence.

Distinguishing between these models of transport could benefit from better understanding of the dynamics of filaments within the NPC. The selective phase and the reduction of dimensionality models both predict that filaments form a mesh-like barrier. The competition or entropic exclusion model has less stringent requirements for movements of the filaments. The Brownian ratchet model (Simon et al., 1992; Mincer and Simon, 2011) requires that the filaments themselves translocate the pore; because it is posited that cargo translocates while bound to the same one or few FG-Nups, those FG-Nups must also translocate. Therefore, the observation of translocation of simulated filaments across the NPC within a biologically realistic model of the FG-Nups was of particular interest.

Our model of the yeast NPC predicts experimental observables that may be relevant for resolving between the models of transport. The simulated FG-Nup filaments, as assayed by autocorrelation functions, were shown to exhibit properties similar to FG-Nups in vivo, as assayed by anisotropy (Atkinson et al., 2013). Nup116 and Nup159 showed a decrease in orientational rigidity along their length both in vivo and in our computational model. In the simulation, this decrease occurred regardless of the simulated strength of the FG–FG bond. In contrast, the experimentally observed orientational freedom of Nup57 did not decrease along its length. This experimentally observed behavior of Nup57 was recapitulated in this model for FG–FG bond strengths of FG4, FG5, and FG6. However, in the absence of FG–FG bonds, the orientational freedom was predicted to decrease along the length. The dependence of the behavior of this FG-Nup on FG–FG bonding indicates a difference in local environment. Either way, the different behaviors of these Nups recapitulate their distinct behaviors in vivo and illustrate the capability of our model to reproduce behaviors of the filamentous FG-Nups. In the study by Atkinson et al. (2013), the differences in the orientational freedoms of different Nups were attributed to their anchor’s location along the nuclear–cytoplasmic axis. For example, Nup57 is anchored in the middle of the channel and is relatively short. Therefore, its tip does not experience the orientational freedom of extending out of the pore as frequently as the tips of Nup116 and Nup159, which are longer and more peripherally anchored. As shown in our data, the nematic order is much higher in the interior of the NPC, so filaments located there will have less decay in their autocorrelation functions.

Signatures of existing qualitative models emerge during this simulation. When FG–FG binding is strong, a gel reminiscent of the selective phase model forms. When the FG–FG off rate is low, the FG-Nups form a dynamic barrier reminiscent of the entropic exclusion model. Therefore, our model enables a more quantitative formulation by which to distinguish between qualitative models. By correlating the model parameter space with signatures of qualitative models, prediction of experimental observables through simulation becomes possible.

The strongest FG–FG–binding condition (FG4) increased the density of FG-Nups within the lumen of the NPC and decreased nematic order, meaning that when the filaments were more cross-linked and in a mesh-like condition, they were less aligned and showed less order. The central channel was also less pronounced in these simulations. These results differ from earlier work by Moussavi-Baygi et al. (2011), where the authors increased the densities of FG motifs on their filaments and found that this modification was not sufficient to create a channel-filling hydrogel. The construction of our model differs from the 2011 Moussavi-Baygi model in several key respects: our model is 3D instead of two dimensional, and our filaments are based on the actual protein sequences of yeast FG-Nups, with heterogeneity in length, binding site locations, and anchor positions.

Faster FG–FG off rates yielded more dynamic filaments with a very low degree of cross-linking. These less stable FG–FG interactions showed little statistical difference from the absence of FG–FG interactions (FG_off). These weaker bonds demonstrated a decrease in the density of FG-Nups located within the lumen of the pore and an increase in nematic order. Less cross-linking was therefore seen to result in a more ordered liquid-crystal like state and a central channel of decreased density relative to the rest of the pore lumen. The simulations of Tagliazucchi et al. (2013) produced a similar central channel, which they attributed to electrostatic interactions; however, we observe a similar channel within the lumen that develops in the absence of any electrostatic interactions simply because of the arrangement and polymer-like properties of the FG-Nup filaments. In recent simulations, the electrostatic content of the FG-Nup amino acid sequence has been predicted to affect the FG-Nup distribution by preventing the aggregation of FG-Nups and ensuring that FG-Nups are evenly distributed and free to move by Brownian motion (Peyro et al., 2015a). Although we do not explicitly model electrostatic forces, we have calibrated our simulations such that the end-to-end distances match previously modeled NSP1 that did incorporate the electrostatic and hydrophobic interactions (see Materials and methods). Thus, our simulations implicitly incorporate the effects of these charges. However, coarse-grained modeling that indicates that charges are not homogenously distributed in the NPC (Tagliazucchi et al., 2013) together with a study reporting the strong effect of heterogeneous charge and hydrophobicity in a polymer-coated nanopore (Huang and Szleifer, 2017) suggest a possible effect of nonuniform charge distribution on the FG-Nup dynamics. We look forward to explicitly incorporating charge in future simulations, to determine what effect it might have on our filament dynamics and filament interactions with specific and nonspecific cargo.

The actual FG–FG off rate in the biological context of the NPC is not known. A quantitative measure of this off rate might help to address the amount of cross-linking within the NPC. To the extent that recent experimental evidence points to an increased nematic order within the NPC (Atkinson et al., 2013), one can speculate, based on our results, that this evidence favors an FG-Nup organization that is relatively not cross-linked. The results point to the need for more in vivo work to further elucidate FG-Nup dynamics, which these results suggest could ultimately lead to differentiation between competing models of the mechanism of selective transport and its relation to FG-Nup behavior. The population of FG–FG–binding sites is heterogeneous, including four main groups (FxFG, FG, GLFG, and PxFG, where x is any amino acid), and different binding strengths between different repeats have been reported in the literature (Xu and Powers, 2013). The difference between the FG-repeat types remains an unexplored parameter in this model, although the ability to modulate binding strengths between different types of FG sites independently is encoded in the model and can be explored in future simulations.

The translocation of FG-Nups in our simulation occurred at rates of milliseconds, consistent with the rate of cargo transport, and at frequencies high enough to account for transport, consistent with a Brownian ratchet model. Although our model agrees with another model that predicts quasi-stable structures at the timescale of nanoseconds (Gamini et al., 2014), our model also suggests that the FG-Nups are highly mobile at longer timescales. Our simulation is consistent with a model that suggests that FG-Nups are subject to rapid Brownian motion, with fast local rearrangements on the order of microseconds (Mincer and Simon, 2011; Moussavi-Baygi and Mofrad, 2016) and slower larger-scale rearrangements on the order of milliseconds. Furthermore, our results are inconsistent with the results that suggest that the filaments are relatively stable and form a gel-like meshwork (Zahn et al., 2016). Our results suggest that the Nups are highly flexible, experiencing Brownian motion, regardless of the degree of FG-Nup cross-linking and mesh formation within the pore. Our model’s prediction of the ubiquity of FG-Nups translocating the NPC on timescales similar to that of cargo transport is significant and will hopefully stimulate and guide future experiments.