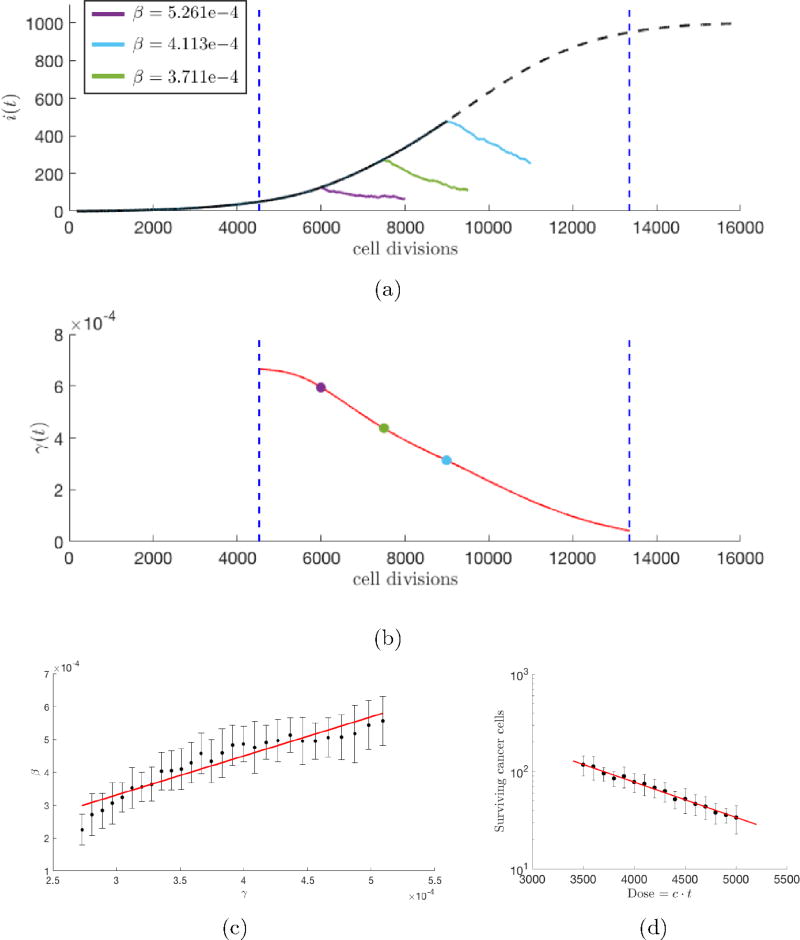
Figure 8.

Growth-dependent tumor regression — (a) An average of 25 stochastic simulations of unperturbed tumor growth (N = 10³ cells, w = 0.5, m = 0.1, no therapy) is plotted (black dashed line) with (b) corresponding instantaneous growth rate, γ(t), of the unperturbed tumor (red). Tumor regression, β, (estimated using an exponential fit of i(t) during therapy, shown in legend) during therapy (constant dose density: c = 1.0, t = 2000) is calculated for a high growth, early-stage therapy (purple), linear-growth, mid-stage therapy (green), and late-stage, slowed growth (light blue); (c) This process is repeated for a full range of growth rates (between vertical blue dashed lines). Average values of β are plotted with standard deviations. Regression is proportional to growth rate (linear fit in red), with higher regression rates associated with high growth rates of early stage tumors. (d) Tumor regression, β, can also be calculated as the slope of a dose response curve (red), where therapy is administered for a range of dose densities (0.7 ≤ c ≤ 1.0) for a single timepoint, 8000 cell divisions (i.e. single growth rate).